一景两图 孰是孰非——从一道单摆习题谈起

郭培东 林晓璐

(漳州台商区第一中学 福建 漳州 363107)

单摆是简谐运动的一个重要应用模型,随着传感器在教学中的普及化,通过传感器显示出单摆在做简谐运动过程中的F-t图像来判断单摆的相关运动规律的习题也越来越多,本文对两道常见的题目进行分析,以期得到更科学的图像.

1 试题的呈现和分析

【例1】一根轻绳一端系一小球,另一端固定在O点(单摆),在O点有一个能测量绳的拉力大小的力传感器,让小球以O点为平衡位置在竖直平面内做简谐运动,由传感器测出拉力F随时间t的变化图像如图1所示,下列判断正确的是( )

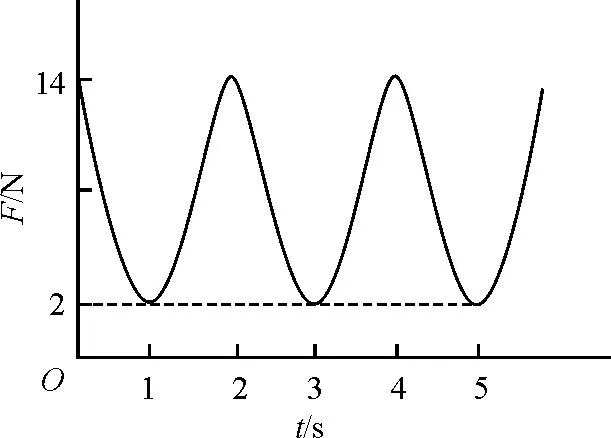
图1 拉力F随时间t的变化图像

A.小球振动的周期为2 s

B.小球速度变化的周期为4 s

C.小球动能变化的周期为2 s

D.小球重力势能变化的周期为4 s

分析与解答：小球振动一个周期经过最低点两次,则周期为4 s,A错误,B正确;由于动能、重力势能均是标量,故在单摆一个周期内它们经过了两个周期,C正确,D错误.

【例2】一单摆做简谐运动,如图2所示为摆绳对摆球的拉力大小F随时间t变化的图像(重力加速度g取10 m/s2),则该单摆的摆长为( )

图2 拉力F随时间t的变化图像

A.0.4 m B.1.6 m

C.4 m D.16 m

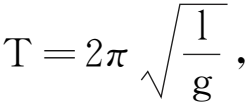
不难看出,以上两道题的命题情景如出一辙,但所画的F-t图像在F最小时却有本质的不同.例1中的F-t图像在此处还是平滑的,例2中的F-t图像在此处出现了尖点.F的最大值出现在小球摆到最低点,F的最小值出现在小球摆到最高点,即两题的命题者在最高点出现了分歧.有些教师认为,图2是对的,图1是错的,理由如下:在小球摆到最高点时,运动状态会突变,速度的方向在这一刻突变,因此F在这一刻应该也是会突变的.针对上述观点,有些教师提出反对意见,他们认为:小球在最高点速度方向会突变,但并不代表运动状态会突变,因为这里面速度是减为零再反方向增加,运动状态是连续变化的,因此F在这一刻应该不会突变的.有些教师认为,图1和图2都对,只是两图的标度选取不同,图2中相同长度的横轴,表示比较长的时间,因此在最高点有点像是被“压缩”了,导致出现了尖点.孰是孰非,针对这些观点和争议,有必要进行进一步探讨和分析.

2 力传感器采集数据 实时画图证明

实验是最具有说服力的证明,尤其是在现如今传感器采集数据,处理数据非常便捷的时代.在高中物理规律的教学中,传感器相较于传统实验器材,具有精度高、误差小、性能稳定、便于展示等特点,更容易实现物理规律的定量探究[1].准备好一单摆实验装置,为了实时显示出绳子拉力大小及其大小变化,在支架上固定一微力传感器,如图3所示.

图3 力传感器采集数据

这里用老虎夹同时夹住力传感器测量头和绳子的一端,保证悬点固定,绳子长度尽量长,固定好铁架台的底座,拉开一个小角度,使小球尽量在一个平面内摆动(因为地转偏向力的存在,这一点只能近似满足),采集了一段数据,为了数据连续变化,采集频率尽量高,且应该是离散点.这里面点选最细的点,频率500 Hz比较合适,截取了其中一段较为理想的数据如图4所示.

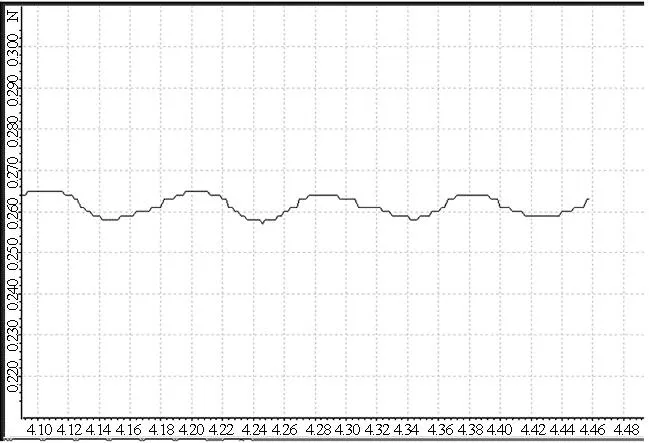
图4 传感器描绘的F-t图像

需要说明的是由于传感器的测量头是竖直固定的,因此拉力传感器的示数只是绳子拉力的竖直分力,从传感器采集的数据可以发现拉力的竖直分力在最高点并没有发生突变,也可以定性证明拉力在此处不会出现“尖点”,是平滑变化过去的.

3 数学推导 Geogebra画图证明

如图5所示单摆.

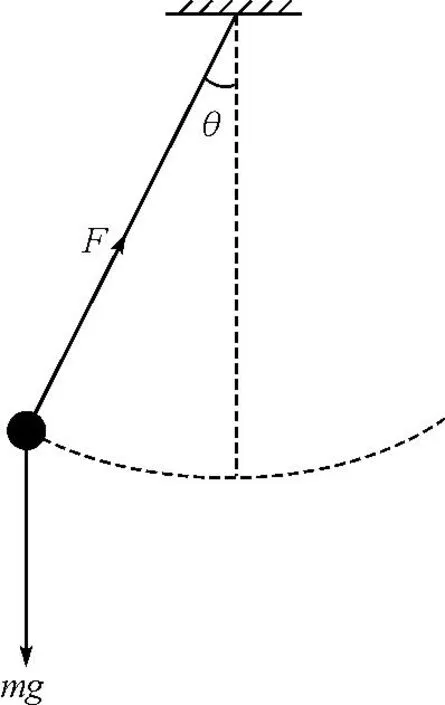
图5 单摆示意图

从最高点开始计时

θ(0)=θ0v(0)=0

设最低点速度为vm

v=vmsinωt

(1)

得

θ=θ0cosωt

(2)

(3)

联立式(1)～(3)得

将

代入得

显然这是一个比较复杂的函数关系式,我们很难直接画出它的图像,为了借用Geogebra的函数功能直接显示出它的图像,各个物理量赋值如下:m=1 kg,g=10 m/s2,θ0=0.01 rad,k=1 N/m,l=1 m,vm=2 m/s(准确的vm应该通过动能定理求解,但vm是一个确定的常数,取2 m/s,不影响F-t图像的大概形状),赋值后的图像如图6所示.

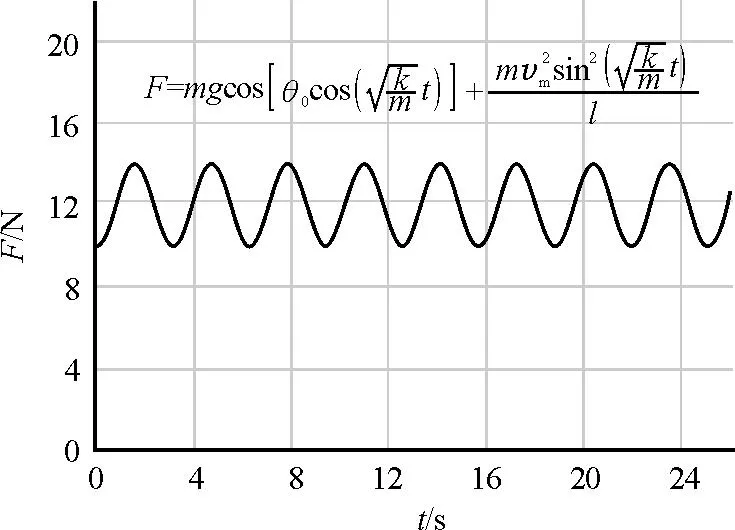
图6 F-t理论推导的图像(Geogebra绘制)

由函数图像易得:绳子拉力F在最低点是平滑变化过去的,F-t图像不应该出现尖点.综上我们可以知道例1的F-t图像是比较准确的,例2的图倒像是人造图,没有科学依据.

4 教学启示

考试命题是对日常教学的检测评估,物理教学需要考虑到考试评价的指导作用,考场上一道好的试题既是检验教师的“教”和学生的“学”的良好载体,更是学生炼化核心素养的重要素材.综合分析,有以下收获和启示.

第一,创设情境,既是考试命题的操作核心,也是物理教学的重要策略,物理学科核心素养的培养,都离不开情境的创设[2].但是“科学性”是试题的生命.有违“科学性”原则的试题是试题命制行为最为尴尬的[3].创设情境最起码要满足“科学性”原则,以免适得其反.

第二,数学方法是物理学最重要的语言,数学不仅为物理学的研究提供了简明、精确的科学通用语言,大大简化、纯化并加速了人们的思维过程,而且还为物理学提供了定量的计算方法,使物理学得以从定性分析的学科发展成为定量分析的精密科学[4].教师在平常教学中遇到的很多疑问都需要用数学方法定量分析给学生一个严谨的证明,甚至需要较高层次的高等数学.

第三,本文通过传感器实时采集数据并画图和通过Geogebra画出复杂的函数图像说明了信息技术可以创设可视化的物理教学情境,培养学生的认知能力,增强学生学习物理的兴趣[5].当然,传感器、Geogebra等信息技术融入教学的功能远不仅于此,教师掌握一定的信息技术可以明显提高教学的便捷性和有效性.