Matlab与实验相结合测量载流圆线圈磁场的新方法探究

徐林超 邓 明 向文丽

(楚雄师范学院物理与电子科学学院 云南 楚雄 675000)

磁场测量技术广泛应用于工业生产[1]、国防建设[2]、医疗[3]、日常生活[4]等多个领域,在各个领域具有重要的应用价值和实际意义.磁场的精确测量对磁场的优化应用可提供一定参考,具有一定实用价值.

传统测量磁场的方法诸多,如霍尔效应法[5]、磁共振法[6]、磁光法[7]和电磁感应法[8],大多数研究报道为亥姆霍兹线圈磁场的理论推导、传统方法测量等[8-9].文献[8]利用传统电磁感应法测量载流圆线圈轴线上的磁场,验证了由毕奥-萨伐尔定律得出的载流圆线圈轴线上磁感应强度公式;文献[9]由线圈中心轴线上的空间磁场分布规律,得到线圈中心轴线上的磁场分布公式,并利用Mathematica得到磁场磁感线分布曲线图.

对于磁场测量的模拟仿真计算,主要为解析法和数值法[10-12],部分以Matlab软件的模拟仿真为基础进行仿真模拟研究[13-14].文献[12]通过分析毕奥-萨伐尔定律并数值计算得到圆线圈和亥姆霍兹线圈的磁场分布曲线;文献[13]通过Matlab数值模拟分析了亥姆霍兹线圈的空间磁场分布,展示了亥姆霍兹线圈磁场在空间中的分布情况;文献[14]通过分析亥姆霍兹线圈轴线磁场的分布规律,建立数学模型,提出利用Matlab软件对亥姆霍兹线圈中心轴线上的磁场分布进行仿真验证的新方法.

当前,对于磁场测量的研究报道主要针对传统方法测量磁场或磁场的模拟仿真计算,利用Matlab仿真计算与实际电磁感应法测磁场实验的新方法报道甚少.文献[15]通过实际实验探究了电容C与亥姆霍兹线圈串联达到谐振测量磁场,一定程度上可以消除交变线圈自身感抗对磁场的影响,从而提高磁场测量的精确度.然而,仅通过实测的方法精确测量磁场存在效率低、指向性不高、针对性不强的问题,如何快速、合理、精确测量磁场是值得我们去探讨并解决的问题.

鉴于此,本文充分利用Matlab仿真数据的优势,设计一种模拟仿真和实际实验相结合测量载流圆线圈磁场的新方法,从而更加高效准确地推广到其他类型的线圈激发的磁场.

1 搭建模型

电磁感应法测量载流圆线圈磁感应强度公式[8]为

(1)

其中,N为探测线圈的匝数,Um是探测线圈感应电动势最大值,S为探测线圈的横截面积,ω为输入频率.

电磁感应法测磁场实验原理如图1所示.

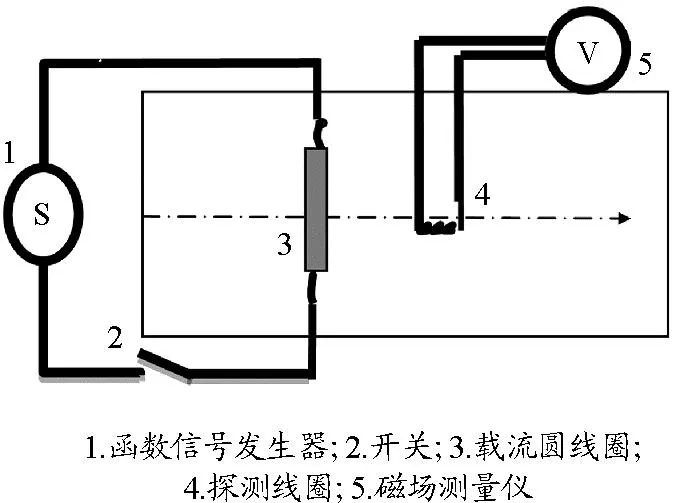
图1 电磁感应法测磁场实验原理图

在传统电磁感应法测载流圆线圈磁场的基础上,与载流圆线圈串联合适的电容C,形成一个标准的RLC串联电路,当达到谐振状态时,感抗和容抗相互抵消,即

(2)

巧妙利用频率,联立式(1)和(2),搭建RLC串联谐振和传统电磁感应法测磁场之间的理想化桥梁,得到

(3)

由毕奥-萨伐尔定律,可知载流圆线圈中心轴线上的磁场理论分布公式为

(4)

其中,μ0为真空磁导率,I为电流,r为线圈半径,X为探测线圈在坐标轴上的位置.因此,理想状态下,感应电动势Um和电容C具有如下关系

(5)

从而,建立了RLC串联谐振和电磁感应相结合测量磁场的理想化模型.

2 Matlab仿真模拟

为了定量研究RLC串联谐振与电磁感应相结合测量载流圆线圈磁场的可行性,将构建的电动势Um与电容C的理想化模型通过Matlab编程仿真[16],并结合本校实验室实验仪器的具体情况,设置载流圆线圈半径r=0.1 m,匝数N=500匝,电感L=95 mH,探测线圈横截面积S=3.6×10-5m2.

选择Matlab仿真的曲线坐标,简化仿真模拟代码的输入过程,令

(6)

得出每个载流圆线圈磁场测量实验平台的位置X对应下的Y值.

由谐振频率公式

(7)

可知,电感L为95 mH,谐振时,其对应的电容C=0.3 μF,考虑到实际实验误差的存在,当磁场测量理想化模型,即式(4)测量磁场误差为5%时,则

(8)

可知,理想化模型的测量误差为5%时,其对应电容为C=0.02 μF.

因此,设置串联电容C的仿真模拟范围为0.02～0.3 μF,当步长为0.01 μF,使用while循环[17],仿真计算

(9)

探究不同大小的电容对感应电动势的影响.

运用Matlab探究不同大小的电容对感应电动势的影响,仿真模拟公式(9),编程如下所示:

Clear

u0=4*pi*10∧(-7);I=0.004;R=0.1;S=3.6*10∧(-5);L=95*10∧(-3);N=500;

x=-0.1:0.01:0.1;

n=numel(x);

i=1;

for i=1:21

a=x(i);

Y(i)=((1+(a/R).∧2).∧(-3/2))

end

Y

C=0.02*10∧(-6);

whileC<0.3*10∧(-6)

fprintf(′value ofC:%d ′,C);

f=(2*pi*(L*C)∧(1/2))∧(-1)

Um=

(S*2*pi*f*u0/2*N∧2*I)/(2*R)*Y;

plot(x,Um)

hold on

title(′载流圆线圈感应电动势分布曲线′)

xlabel(′x/m′);ylabel(′Um/v′);

axis

grid

C=C+0.01*10∧(-6);

end

通过仿真得到载流圆线圈感应电动势分布曲线,如图2所示.

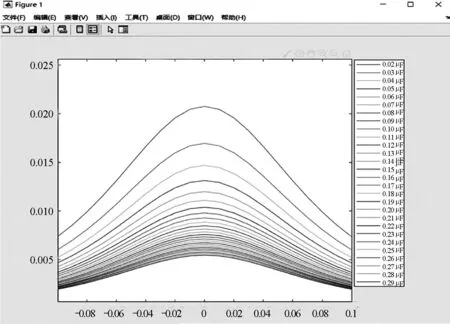
图2 Matlab仿真载流圆线圈感应电动势分布曲线图

图2中,在电容C=0.02 μF到C=0.3 μF的范围内,电容C越小,感应电动势越大,Um分布曲线随着电容C的减小而整体上移,电容C与载流圆线圈串联发生谐振,一定程度上影响感应电动势Um的测量,从而达到改进传统电磁感应法测量磁场的目标.

仿真结果表明:利用RLC串联谐振改进电磁感应法测载流圆线圈磁场的创新设计是科学可行的,并对实际实验的探究以及电容参数的选择具有一定指导意义和参考价值.

3 实验探究

在仿真模型电容参数的参考下,选取串联电容C=0.02 μF到C=0.3 μF范围内的磁场分布进行实际实验探究.

实验原理如图3所示,令电容C和载流圆线圈串联,当开关3闭合时,函数信号发生器输出正弦交流电信号,通过优化选择电容C的大小和载流圆线圈串联,调节频率发生谐振,使载流圆线圈两端的电压达到最大值.将磁场测量仪接入载流圆线圈两端,选择电容C的大小后调节输入频率,通过晶体管毫伏表读数,当其测量值达到最大值时可判断该电路达到谐振;在电路达到谐振时,将探测线圈水平放至载流圆线圈中心轴线上,移动探测线圈至探测点,将磁场测量仪接入探测线圈两端,旋转探测线圈,读出该探测点的感应电动势的最大值,由式(1)得出该探测点的磁感应强度.同时,利用载流圆线圈中心轴线上的磁场分布式(4),得到中心轴线上的磁感应强度理论值,记录于表1.将实际实验效果最佳的串联电容C,分别为0.099 μF、0.100 μF、0.110 μF时的数据记录于表1.

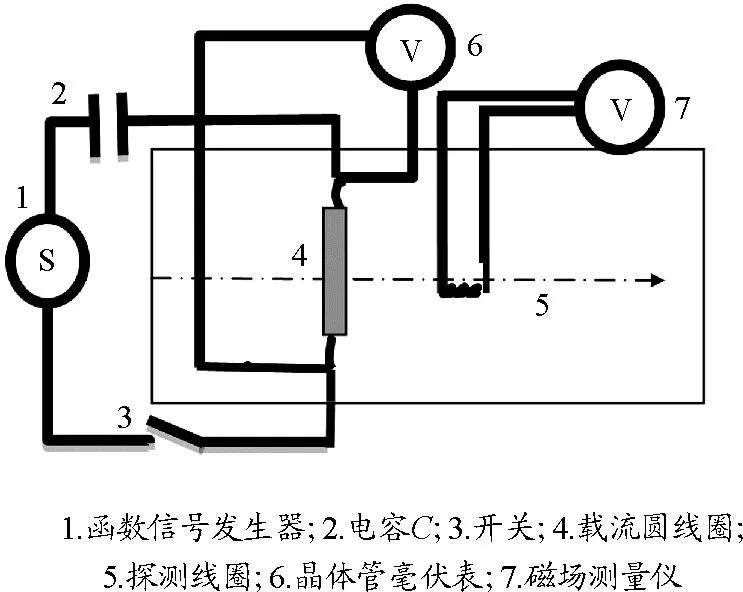
图3 载流圆线圈磁场测量实验原理图

表1 载流圆线圈理论状态、传统法、创新设计的数据记录表

4 实验结果

根据表1所列出的数据,利用Origin软件作出不同串联电容条件下,载流圆线圈中心轴线上的感应电动势分布曲线图和磁感应强度分布曲线图,分别如图4和图5所示.

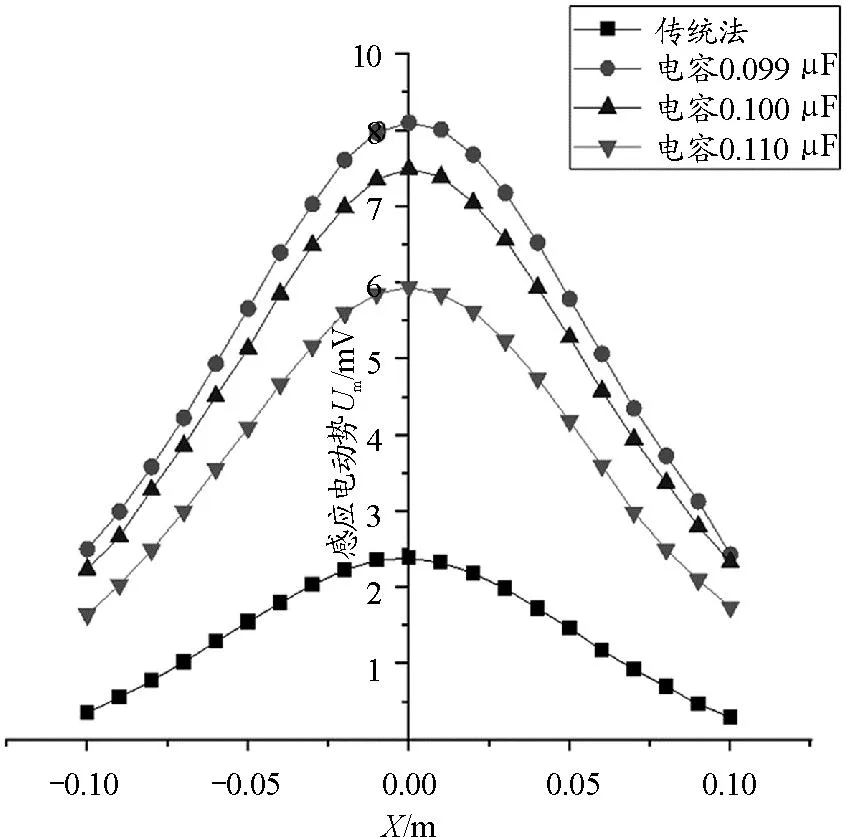
图4 不同串联电容下载流圆线圈中心

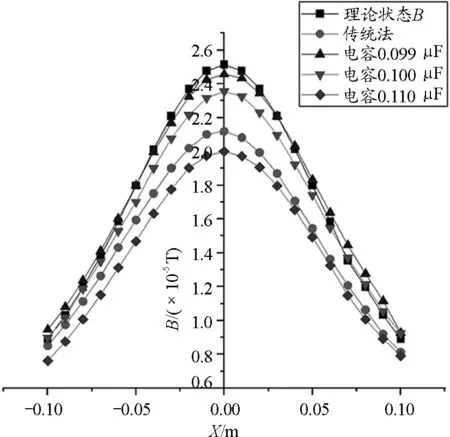
图5 不同串联电容下载流圆线圈中心轴线上

实际实验中,如图4可知,在优化选择的3种不同串联电容下,载流圆线圈中心轴线上的Um分布符合Matlab仿真规律,即电容C越小,感应电动势Um越大.Um实验结果与理论仿真规律吻合.由图5可知,3种不同大小的串联电容中,最小电容即串联电容C为0.099 μF时,载流圆线圈中心轴线上的磁场分布最接近理论状态下的磁场分布,精确度最高,当X=0时,计算误差为2.23%;串联电容C=0.100 μF时,精确度次之,当X=0时,误差为6.29%;最大电容即C为0.110 μF时,该点误差为20.41%.相比传统电磁感应法测磁场(X=0时,误差为15.67%),合理选择串联电容的值,测量磁场的精度提高,当C为0.099 μF时,误差仅为2.23%.

Matlab的模拟仿真对交流线圈磁场的测量有一定的辅助作用,验证了创新设计实验原理科学可行,指导了实际实验的参数选择,提高了实验效率和精确度.串联电容C的选择以实际实验效果为主,Matlab的仿真模拟结果作为参考.

5 结束语

本文基于Matlab对改进的电磁感应法测量载流圆线圈磁场的创新设计科学可行,不用添加新仪器,操作简单,误差小,精确度高.

理论上模拟仿真的谐振频率通过公式而得,但电感有效值的测量精度在一定程度上会对实验测量结果造成影响.因此,实际测量的谐振频率和线圈理论仿真谐振频率具有一定的偏差,不同串联电容C的效果以实际实验探究结果为准,仿真模型作为参考.

基于Matlab与实际实验相结合提供了一种测量交变线圈激发的弱磁场的探究思路,可以作为一种测量交变电流激发的弱磁场的新方法推广至其他类型的线圈激发的弱磁场.利用Matlab模拟仿真与实际实验相结合,两个不同大学物理必做实验项目即RLC串联谐振与电磁感应相结合测量磁场,具有一定创新和深度,可作为一种新增综合设计性大学物理实验的项目进行推广,具有一定的教学推广意义.