例谈杆球问题中机械能守恒的判定*

谭小虎 李秋明 韩小雪 马 颖

(广州大学物理与材料科学学院 广东 广州 510006)

机械能守恒定律是高中物理的重要内容,课标明确要求学生要理解机械能守恒定律,能用机械能守恒定律分析生产生活中的有关问题[1].

杆球问题是高中物理教学中常见的习题类型,该模型中杆的弹力是否做功无法直观判断,导致学生在判定杆球系统机械能是否守恒时存在一定的困难.此外,在杆球问题的处理中,常常会默认杆球系统机械能守恒,而后对其他问题进行求解[2],并不从学生对机械能守恒条件的基本认识出发,对系统机械能是否守恒展开讨论并予以严谨证明.综上,杆球问题在一定程度上成了学生学习和理解机械能及其守恒定律的障碍.

本文以两个典型的杆球问题为例,针对常见的杆球问题情境,先运用刚体力学知识对问题进行分析和研究[2],明确问题情境中各个力做功的情况,据此判定杆球系统机械能守恒,而后尝试从高中物理的角度给予严谨证明,深化学生对机械能守恒定律和杆球问题的理解.

1 机械能守恒的条件

在惯性参考系中,质点系所受外力做的功与系统内非保守力做的功的总和等于质点系机械能的增量[3],即当质点系所受外力和非保守内力做功为零时,其机械能的增量为零,此时机械能守恒,因此明确何种力为非保守力是判定机械能是否守恒的基础.为了可以简易地判断常见的力是否为非保守力,赵凯华编著的《新概念物理教程:力学》[4]给出了保守力的一些充分条件:

(1)对于一维运动,位置x单值函数的力是保守力,例如服从胡克定律的弹性力;

(2)对于一维以上的运动,大小和方向都与位置无关的力是保守力,例如重力;

(3)凡是有心力都是保守力.

普通高中物理教科书中关于机械能守恒有如下叙述,在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变[5].

综上,本文研究对象是一个不包含弹簧的杆球系统,该系统机械能守恒的条件可以认为是只有重力做功.下文将以此条件作为机械能守恒的判定依据.

2 杆球问题中机械能守恒的判定

【例1】如图1所示,长为2L的质量不计的轻杆,一端与O点铰接,轻杆可绕着O点在竖直平面内无摩擦转动,杆的中点和另一端均固定有质量为m的可视为质点的小球,将杆分为L1和L2两部分.现将杆拉至水平位置并无初速度释放,忽略空气阻力.问:从轻杆开始下摆到下摆至竖直位置的过程中,轻杆和小球组成的系统机械能是否守恒?

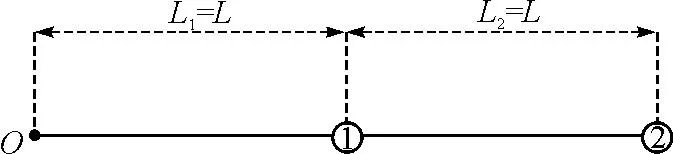
图1 例1示意图

在下摆的过程中,若轻杆对小球的弹力方向始终沿杆,一直与小球速度方向垂直,则轻杆弹力不做功,杆球系统中只有重力做功,该系统机械能守恒.但轻杆弹力是否沿杆还有待分析.

在高中阶段,认为带有铰链的可以在一定范围内自由转动的轻杆,其弹力方向一般沿杆[6].显然,图1中轻杆的转动并不完全自由,L1杆的运动除受铰链约束外,还受到小球和L2杆的约束,同样,L2杆也受到了L1杆和小球的约束,若仅仅因为L1杆铰接于O点便认定L1杆和L2杆弹力的方向均沿杆,未免过于牵强.下面,将分别从刚体力学和高中物理两个角度对上述问题展开分析.

(1)刚体力学角度分析

杆球系统的转动惯量为

J=mL2+m(2L)2=5mL2

(1)

设某时刻,轻杆与小球已经下摆了θ的角度,此时系统的角加速度为α,由转动定律得到此时的角加速度

mgLcosθ+mg·2Lcosθ=5mL2α

(2)

(3)

摆角θ的取值范围为0～90°,可知α>0,两小球处于加速的状态.

由于不确定两杆弹力方向是否沿杆,即不确定两杆弹力是否存在切向分量,故假设L1杆对球1存在切向弹力F1,L2杆对球1和球2存在切向弹力分别为F2和F3.其中L2杆质量不计,可认为它不具有加速度而处于受力平衡状态,因此假设F2和F3方向相反、大小相等,即

F2=F3

(4)

系统所受切向力的示意图如图2所示,其中3个切向弹力的方向均为假设.

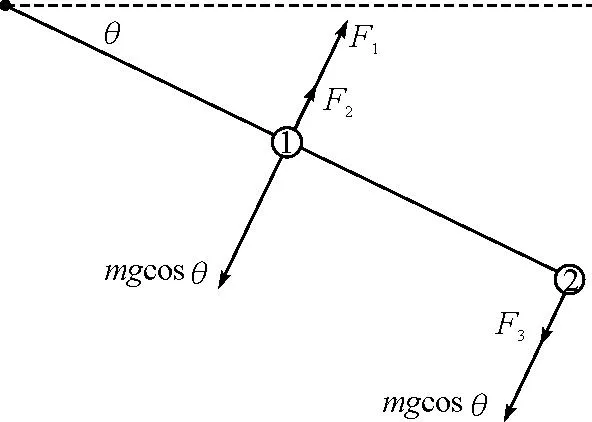
图2 例1切向受力示意图

设球1和球2的切向加速度分别为a1和a2,两球正在加速,因此它们的切向加速度均垂直于轻杆向下.结合式(3)对球1和球2切向受力由牛顿第二定律得

mgcosθ-F1-F2=ma1=

(5)

mgcosθ+F3=ma2=m·2Lα=

(6)

联立式(4)～(6)得

(7)

3个切向弹力均为正值,可知图2中切向弹力方向假设正确.

由图2可知,F1和F2始终与球1运动方向相反,F3始终与球2运动方向相同.设3个切向弹力在此运动过程中的总功为W,该总功计算如下

(8)

可见轻杆切向弹力对两球所做的总功为零,即在此过程系统中只有重力做功,该系统机械能守恒.

(2)高中物理角度分析

设某时刻,杆球系统下摆了θ的角度,其中θ为微小角度,可得杆球系统在此过程中处于加速的状态,即两球此时的切向加速度均垂直于轻杆向下.

设球1和球2的切向加速度分别为a1和a2,利用微元法对a1和a2的大小关系展开分析,两球做圆周运动的过程中,球2线速度大小始终是球1线速度大小的两倍,在极短时间内,可认为两球均做匀加速直线运动,得到

a2=2a1

(9)

切向受力示意图如图2所示,其中3个切向弹力的方向均为假设.

为分析3个切向弹力之间的关系,将L1杆和L2杆视为整体进行分析.忽略它们的质量,可知它们不具有加速度,因此它们在小球切向弹力的作用下处于杠杆平衡状态,由杠杆平衡原理及牛顿第三定律可得

(F1+F2)L=F3·2L

(10)

联立式(4)和式(10)得

F1=F2=F3

(11)

对球1和球2切向受力由牛顿第二定律得

mgcosθ-F1-F2=ma1

(12)

mgcosθ+F3=ma2

(13)

联立式(9)、(11)、(12)、(13)得

(14)

由于θ的取值范围为0～90°,可知cosθ>0,即3个切向弹力均为正值,图2中切向弹力方向假设正确.

观察图2可知,F1和F2始终与球1的运动方向相反,F3始终与球2运动方向相同.利用微元法展开分析,以Δs表示球1在极短时间内的位移,则球2的位移为2Δs,设3个切向弹力在极短时间内的总功为W,该总功计算如下

W=-F1Δs-F2Δs+F3·2Δs=

(15)

在极短时间内,轻杆切向弹力对两球所做总功为零,由微元法可知在运动全过程中轻杆切向弹力的总功也为零,系统中只有重力做功,该系统机械能守恒.

【例2】如图3所示,质量不计的直角形支架两端分别连接着可视为质点的质量为m和2m的小球1和2,支架的两直角边长度分别为2L和L,支架可绕着O点在竖直平面内无摩擦转动,开始时,长度为2L的直角边位于水平位置,由静止释放,忽略空气阻力.问:从支架开始转动到转动90°的过程中,支架与小球组成的系统机械能是否守恒?

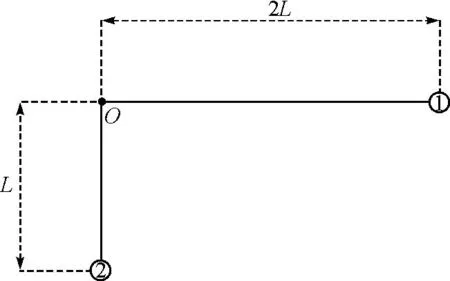
图3 例2示意图

(1)刚体力学角度分析

支架与小球组成的系统的转动惯量为

J=m(2L)2+2mL2=6mL2

(16)

设某时刻,系统已经下摆了θ的角度,此时系统的角加速度为α,由转动定律得到此时的角加速度

mg·2Lcosθ-2mgLsinθ=6mL2α

(17)

(18)

假设支架施加给球1的切向弹力为F1,施加给球2的切向弹力为F2.切向受力示意图如图4所示,其中切向弹力的方向均为假设.

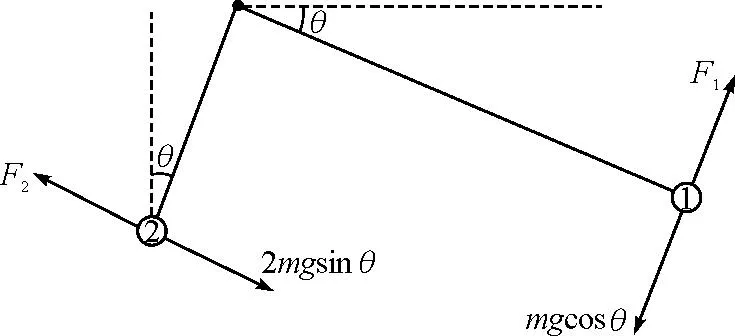
图4 例2切向受力示意图

设球1和球2的切向加速度分别为a1和a2,对球1和球2切向受力由牛顿第二定律得

mgcosθ-F1=ma1=

(19)

F2-2mgsinθ=2ma2=

(20)

由式(19)和式(20)得

(21)

(22)

由于θ的取值范围为0～90°,得两个切向弹力均为正值,图4切向弹力方向假设正确.

由图4可知,F1始终与球1的运动方向相反,F2始终与球2运动方向相同.设两个切向弹力在此运动过程中的总功为W,总功的计算如下

(23)

可见支架切向弹力对两小球所做的总功为零,即在此过程系统中只有重力做功,该系统机械能守恒.

(2)高中物理角度分析

设某时刻,支架与小球已经下摆了θ的角度,其中θ为微小角度,可得杆球系统在此过程中处于加速的状态,即两球此时的切向加速度均垂直于轻杆向下.

以a1和a2分别表示球1和球2的切向加速度.利用微元法对a1和a2的大小关系展开分析,两球做圆周运动的过程中,球1线速度大小始终是球2线速度大小的两倍,在极短的时间内,可认为两球做匀加速直线运动,可得

a1=2a2

(24)

切向受力示意图如图4所示,切向弹力的方向均为假设.对球1和球2切向受力由牛顿第二定律得

mgcosθ-F1=ma1

(25)

F2-2mgsinθ=2ma2

(26)

联立式(25)和式(26)得

F1+F2=mg(cosθ+2sinθ)

(27)

为分析两个切向弹力之间的关系,隔离支架进行分析.忽略支架质量,可知它不具有加速度,因此它在小球切向弹力作用下处于杠杆平衡状态,由杠杆平衡原理及牛顿第三定律可得

F1·2L=F2L

(28)

联立式(27)和式(28)可得

(29)

(30)

由于θ的取值范围为0～90°,得两个切向弹力均为正值,图4切向弹力方向假设正确.

由图4可知,F1始终与球1的运动方向相反,F2始终与球2运动方向相同.利用微元法展开分析,以2Δs表示球1在极短时间内的位移,则球2的位移为Δs,设两个切向弹力在极短时间内的总功为W,总功计算如下

W=-F1·2Δs+F2Δs=

(31)

可见在极短时间内,支架切向弹力对两小球所做总功为零,由微元法可知在运动全过程中支架切向弹力的总功也为零,系统中只有重力做功,该系统机械能守恒.

诚然,在学生经历除机械能以外的诸如电能、内能等其他形式能量知识的学习以后,他们能够判断本文的杆球情境中不存在非机械能的能量转化,可从能量守恒的角度直接判定系统机械能守恒,但杆球系统机械能守恒的判定问题不应留待后期解决.高中物理教学中的每一阶段都有其阶段性的教学和培养目标,杆球问题出现在学生只掌握牛顿运动定律和机械能相关知识的阶段,教师就应当从学生的现有知识基础出发寻求合适的教学思路.

3 结束语

本文先运用基础较好的学生能够理解的刚体力学知识分析、解决杆球系统中机械能守恒的判定问题,虽然刚体力学角度的分析难度较大,但为高中物理角度分析的展开提供了思路.而后从所有学生的知识基础出发,从高中物理的角度重新分析并解决杆球系统中机械能守恒的判定问题,整个分析过程仅使用微元法、杠杆平衡原理和牛顿运动定律等知识,比较适合高中教学,有利于巩固学生已学知识,培养科学思维.希望本文的分析过程能够为杆球问题的教学提供一定的参考.