结合人工蜂群与K-means聚类的特征选择
2024-01-11刘梦含薛占熬
孙 林,刘梦含,薛占熬
1.天津科技大学 人工智能学院,天津 300457
2.河南师范大学 计算机与信息工程学院,河南 新乡 453007
近年来,高维数据增大了计算机的存储压力,而且存在诸多不相关及冗余数据[1]。特征选择是数据挖掘过程中预处理的一个重要步骤,其目标是从原始数据集中找到最大相关最小冗余的特征,实现降维。根据是否使用类标信息,特征选择算法分为有监督和无监督[2]。传统的有监督特征选择算法通过不同的判断准则衡量特征之间的相关度和冗余度,进而去除不相关和冗余特征。其对无标签数据不适用。无监督特征选择算法不需要事先知道类标,因此进行无监督特征选择更具普适性。
聚类是数据挖掘中重要的无监督分类方法,其中K-means 聚类具有实现形式较简单、线性计算复杂度低等优点[3]。由于其优势而被广泛应用于工业、医学、军事等领域,但也存在缺点:对初始聚类中心选择敏感、易陷入局部最优等。Redmond 等[4]将估算出密度最大的样本作为初始中心,实现优化K-means聚类,但其易陷入局部最优解的问题未得到解决。隋心怡等[5]将样本分布空间分割为大小相同的子空间,统计子空间中的样本密度优化初始聚类中心,但该算法的聚类结果受参数影响较大。邵伦等[6]将样本集映射到虚拟的多维网格空间结构中,从中选择包含样本数最多且距离较远的子网格作为初始聚类中心网格,解决容易陷入局部最优的问题,但该算法结果依赖于单一的相似性度量。廖纪勇等[7]通过定义均值相异性和总体相异性准则确定初始聚类中心,该算法改善了离群点对聚类结果的影响,但未解决易陷入局部最优的问题。因此,受上述文献启发,引入群智能优化算法改进K-means 聚类算法,弥补初始聚类中心的选取敏感的缺陷,并改善其全局搜索能力。
近年来,群智能优化算法由于其操作简单、收敛速度快、全局收敛性好等优势[8-11]而被众多学者运用到聚类中[12]。它能解决K-means 算法对初始聚类中心过度依赖以及其易陷入局部最优解的问题。2005年,Karaboga[13]提出人工蜂群(artificial bee colony,ABC)算法,模拟蜜蜂采蜜的群体智能优化。其具有原理简单、控制参数少、鲁棒性强和全局搜索能力强等优势[14]。一些研究[15]结果表明,ABC算法在求解连续优化问题时性能优于蚁群优化(ant colony optimization,ACO)[16]和粒子群优化(particle swarm optimization,PSO)[17]。近年来,一些学者利用ABC 的优点与K-means 聚类相结合改进算法性能。Janani 等[18]设计了一种结合ABC 和平分K-means 聚类的混合算法,但该方法在计算距离时仍采用传统的欧氏距离未能有效提高距离计算的精确性。Jin等[19]在ABC中引入模拟退火准则,提高了算法的收敛速度,但该方法未能有效提高局部搜索能力。曹永春等[20]通过调整反向学习的初始化策略和邻域搜索范围改善ABC,进而提高K-means聚类算法的稳定性,但该算法中的参数需要根据经验选取。因此,受上述文献启发,构造新的适应度函数,对引领蜂和跟随蜂的食物源搜索范围进行动态调整,改进ABC算法,以满足不同进化时期蜂群对全局寻优能力和局部寻优能力的不同要求,加快收敛速度;同时考虑两个空间向量之间的累积差异和对应向量之间的相似性,设计新的欧氏距离。
对特征进行聚类有助于发现特征之间的内在联系,而且形成的特征簇通常对应一些潜在的相关特征[21]。因而,众多学者使用聚类进行特征选择。Du等[22]结合ABC 与K-means 算法进行特征子集选择,提高了算法的分类精度,但该算法所选特征不能保证最小冗余。Moslehi 等[23]利用K-means 聚类算法选择数据集中有效特征并去除不相关的特征,但该方法在进行特征选择时未考虑特征与样本之间的关系。Tang等[24]利用基于余弦距离的K-means聚类对特征进行聚类,选择最优特征子集,但该算法的参数需要人工设置。胡敏杰等[25]利用谱聚类将特征进行分簇,使用邻域互信息从每一特征簇中选择特征子集,但该方法仅在低维数据集上进行了分类能力的测试。因此,受上述文献的启发,提出了特征重要度衡量特征,以选择到最优特征子集。
为此,借助改进的ABC 和K-means 聚类的优势,本文提出结合改进的ABC 与K-means 聚类的特征选择算法。其主要贡献如下:
(1)为了衡量蜜源质量和选择初始聚类中心,定义簇内聚集度和簇间离散度,构造了蜜源位置的适应度函数,引导蜂群向高质量蜜源全局搜索,把蜂群每次迭代得到的最优蜜源位置作为K-means 聚类的初始聚类中心,并在此基础上进行交替聚类,使相似性强的点聚在同一类簇中。
(2)为了加快ABC 的收敛速度,并且解决蜂群在进行邻域搜索时,位置更新在相对固定范围内没有具体的搜索范围和方向,通过对蜂群邻域搜索范围的动态调整,构造了新的蜜源位置更新表达式,使之更符合蜂群在蜜源搜索的实际情况。
(3)通过考虑两个空间向量之间的累积差异以及对应向量之间的相似性,设计了新的欧氏距离;定义了特征区分度与特征代表性,并以二者之积度量特征重要性,选择特征重要度大的特征构造最优特征子集。
1 相关基础知识
1.1 人工蜂群算法
ABC 算法主要由4 个要素组成:蜜源、引领蜂、跟随蜂和侦察蜂[12]。并且具有3 种基本的行为模式:搜索蜜源、招募蜜蜂和放弃蜜源[14]。其算法的主要步骤可以参照文献[15],主要包括4 个阶段:
(1)初始化蜂群阶段
设有n个蜜源的初始种群为X={X1,X2,…,Xn},每个蜜源Xi={Xi1,Xi2,…,Xid}是一个d维向量,蜜蜂总的循环搜索次数为MCN,每个蜜源可被重复开采的次数为limit。随机产生n个解,并计算相对应解的适应度值,将适应度由大到小的顺序进行排列,其中前一半作为引领蜂,后一半作为跟随蜂。其中蜜源Xi随机产生的表达式为:
(2)引领蜂阶段
在引领蜂阶段,引领蜂在当前所在位置进行邻域搜索,产生新的位置作为候选蜜源,并计算其适应度。引领蜂的位置搜索表达式为:
其中,表示引领蜂进行邻域搜索产生的新位置,新蜜源Vi=(Vi1,Vi2,…,Vid),p∈{1,2,…,n},j∈{1,2,…,d},p和j是从各自相应的范围内随机选取的两个数,是在区间[-1,1]之间控制邻域搜索范围而进行随机选取的数,同时决定扰动的幅度。通过式(2),引领蜂得到新蜜源,再利用贪婪原则选择蜜源。其贪婪原则是:如果搜索到新蜜源Vi的适应度高于原蜜源Xi,则Vi替换Xi;反之,蜜源Xi不变。
(3)跟随蜂阶段
在引领蜂完成邻域搜索之后,会在舞蹈区分享蜜源信息。跟随蜂根据其分享信息,采用轮盘赌选择策略从引领蜂搜索的蜜源中选择跟随蜜源,以保证适应度越高的蜜源被开采的几率更大。在开采的过程中,跟随蜂与引领蜂一样通过式(2)寻找新的蜜源,留下适应度更高的蜜源。蜜源被选择的概率为:
(4)侦察蜂阶段
如果蜜源经过多次迭代后其质量没有进行更新,并且迭代次数达到规定上限,则表明该蜜源陷入局部最优解,将抛弃蜜源。与此同时,与之对应的引领蜂转换为侦察蜂,根据式(1)产生新蜜源代替该蜜源。当完成全部迭代后,适应度值最大的蜜源就是问题的最优解,算法结束。
1.2 K-means聚类算法
K-means 聚类是一种经典的基于划分的聚类方法[7]。其主要思想是:在给定的数据集中,首先随机选择K个初始聚类中心,利用欧氏距离计算各个样本之间的距离,根据距离最近原则将样本分为K个簇;然后求出每一簇的平均位置,重新分配聚类中心,当迭代达到规定次数或者聚类中心不再发生变化,则聚类结束并输出结果。其详细步骤可以参考文献[19]。传统的K-means 聚类算法的初始聚类中心随机选取,并且该算法是通过迭代获得最优解,初始聚类中心的不同导致聚类结果也不相同,会造成聚类结果的不稳定。因此,如何选择恰当的初始聚类中心是改进K-means 聚类算法的一个重要研究方向[20]。
假设数据集D∈Rn×d,其中n表示样本数,d表示特征维度,{f1,f2,…,fi,…,fd} 表示d维特征向量,{x1,x2,…,xj,…,xn}表示n个样本的集合,则该数据集也可以表示为D={x1,x2,…,xi,…,xn},且xi∈Rd,xi=(xi1,xi2,…,xid)。若将D划分为多个类C={C1,C2,…,CK},K为D划分的簇数且,则基于划分的聚类分析目标函数为:
2 提出的特征选择方法
2.1 适应度函数
在ABC 算法中,适应度函数直接决定蜂群进化的行为、迭代次数和蜜源的质量,同时也引导蜂群进化的方向[14]。当适应度函数不相同时,得到的蜜源质量也不相同。一般情况下,适应度函数值越大则说明蜜源含蜜量越多,也代表蜜源所处位置越好,越能吸引蜜蜂。
文献[15]指出:传统的适应度函数仅仅考虑簇内各个样本的特性,未考虑簇间样本的特性,则不能全面反映数据集中各个样本的特征。由此,在聚类簇中,为了使同一簇中样本的相似度高而不同簇中样本的相似度低,下面通过簇内聚集度和簇间离散度函数构建新的适应度函数。
定义1(簇内聚集度函数)设数据集D={x1,x2,…,xn},K个聚类中心CK={m1,m2,…,mK},则簇内聚集度函数为:
其中,xi表示任意样本,mK表示CK的聚类中心。
定义2(簇间离散度函数)设数据集D={x1,x2,…,xn},K个聚类中心CK={m1,m2,…,mK},则簇间离散度函数为:
其中,mi和mj表示所有簇中任意两个聚类中心。由此可知,簇间离散度越大则表示不同簇之间的距离越大,相似度越低,聚类效果越好,反之亦反。
由文献[15]可知:簇内聚集度越大表示同一簇中的样本相似度越低,反之亦反。另外,簇内聚集度函数的最优解是簇内所有样本到其所属簇总聚类中心的距离之和最小。由此,为了同时考虑簇内特性和簇间特性,下面设计新的适应度函数。
定义3(适应度函数)设数据集D={x1,x2,…,xn},K个聚类中心CK={m1,m2,…,mK},则新的适应度函数表示为:
其中,J(CK)表示簇内聚集度函数,D(CK)表示簇间离散度函数。由式(7)可知,簇间离散度越大,簇内离散度越小,适应度数越大,聚类效果越好。
定义4(基于新的适应度函数的概率表达式)设数据集D={x1,x2,…,xn},则蜜源被选择的新的概率表达式为:
其中,fiti表示第i个蜜源的适应度,i=1,2,…,n。
2.2 邻域搜索范围
在传统的ABC 中,依据式(2)更新引领蜂和跟随蜂的位置,使它们在一个相对固定范围内进行蜜源随机搜索,没有具体范围和方向,这样就造成了它们进行位置搜索时具有茫然性。在实际搜索中,在不同时期蜜蜂进行蜜源搜索的范围和方向都不尽相同,由此需要改进原始的蜜源搜索方式,以确保蜜蜂在蜜源搜索的过程中更符合实际情况。在初始阶段,ABC 希望引领蜂的搜索范围相对较大,能很快地找到最优解的大致方位;随着迭代次数的不断增加,ABC 进入最后阶段,由于此时搜索范围已经靠近最优解,于是希望后期蜜蜂能够在最优解附近搜索,从而更准确地搜索到最优解位置。综上所述,引领蜂和跟随蜂在蜜源搜索初期,其范围应尽量大,在搜索后期,其范围应减小。
定义5(邻域搜索表达式)设数据集D={x1,x2,…,xn},则邻域搜索表达式为:
其中,M表示非线性递减的邻域范围调整系数,M=a-t,a>1,根据文献[26]对邻域范围调整系数策略进行测试,获取最优参数值为1.1;表示引领蜂搜索后随机产生的邻域蜜源的位置;表示当前蜜源的位置;表示在[-1,1]之间的随机数,同时决定扰动的幅度;t表示当前迭代次数。
由定义5 可知,在改进ABC 的迭代初期,t较小则M较大,蜜蜂在较大邻域范围内进行搜索,全局搜索能力比较强;在迭代后期t变大则M变小,蜜蜂在较小邻域范围内进行搜索,局部搜索能力较优。因此,式(9)满足了蜜蜂在不同进化时期对其寻优能力的要求,增强了跳出局部最优值的能力,加快了算法的收敛速度。考虑到随着迭代次数增加而权值逐渐减小的情况,文献[27]和文献[20]中也对邻域搜索表达式中的权值进行了改进,其权值依赖于经验值,但是式(9)中的权值M是通过实验测试获取。因而,与文献[27]和文献[20]中的权值相比,上述式(9)中的权值M更加具有普适性和合理性。
2.3 加权欧氏距离
传统的K-means 聚类样本之间的相似程度通常是根据欧氏距离进行衡量的。在一般情况下,样本之间的欧氏距离越小则表示样本相似度越大[3]。但是,这种划分准则仅仅考虑两个样本之间的累积差异,具有一定的局限性。为此,在计算样本之间的距离时,既要考虑两个向量之间的累积差异,还要充分考虑对应样本之间的相似性。于是,下面设计了基于特征和样本相似性的欧氏距离计算表达式。
定义6(基于特征的加权欧氏距离)设数据集D={x1,x2,…,xn},样本xi=(xi1,xi2,…,xid),xj=(xj1,xj2,…,xjd),则依据特征影响程度不同的加权欧氏距离表达式为:
定义7(基于样本相似性的加权欧氏距离)设数据集D={x1,x2,…,xn},样本xi=(xi1,xi2,…,xid),xj=(xj1,xj2,…,xjd),则基于样本相似性的加权欧氏距离表达式为:
由定义7 可知,式(11)表示数据集中各样本之间的特性,对应样本越相近,则其相似度的贡献越大,在最终相似度结果中占有更大的比重。但是,式(10)和式(11)这两个加权欧氏距离仅从数据集中样本或特征单方面进行考虑,于是结合式(10)和式(11)构建混合的加权欧氏距离公式,使其能更全面地反映出数据集的总体特性。
定义8(基于特征和样本相似性的加权欧氏距离)设数据集D={x1,x2,…,xn},样本xi=(xi1,xi2,…,xid),xj=(xj1,xj2,…,xjd),对任意样本xi和xj,则依据各分量影响程度不同和样本的相似性加权定义样本xi和xj之间的加权欧氏距离表达式为:
2.4 特征重要度
定义9(特征区分度)设数据集D={x1,x2,…,xj,…,xn},fi∈Rn,则特征区分度表示为:
其中,fji表示样本xj在特征fi上的取值,i=1,2,…,d,j=1,2,…,n。
文献[21]指出:Pearson 相关系数可以度量两变量之间的相关性,其绝对值越小则越不相关。当它们的Pearson 相关系数为0 时,不能判定这两个变量是独立的,有可能是非线性相关。但是,当它们的距离相关系数是0,就可以说这两个变量是独立的。为解决该问题,采用距离相关系数判断两个特征之间的相关性[1],利用特征与特征之间的距离系数的倒数作为特征代表性,于是该特征代表性越强则表明两个特征相关性越弱。
为了同时考虑样本与特征之间的关系以及特征与特征之间的关系,下面构造特征重要度。
定义11(特征重要度)设数据集D={x1,x2,…,xj,…,xn},fi∈Rn,基于特征区分度与特征代表性之积定义特征fi的重要度scorei为:
其中,disi表示特征区分度,rei表示特征代表性。
由定义11 可知,当特征fi的特征区分度与特征代表性越大时,则特征fi的重要度值越大。文献[21]指出:重要的特征应该使同类样本之间的特征值相同或相近,而不同类样本之间的特征值不同或者差别很大。也就是说,重要度大的特征应该具有较大的区分度和较大的代表性。
2.5 算法描述
结合改进的ABC 与K-means 聚类设计特征选择算法(feature selection usingK-means clustering with artificial bee colony,FSKCA),其伪代码描述如算法1所示。主要由3个部分组成:基于改进人工蜂群的优化算法(Improved artificial bee colony algorithm,IABC)的具体过程见步骤1~步骤28;基于改进人工蜂群的K-means 聚类算法(improved artificial bee colony-basedK-means clustering algorithm,IABCK)的具体过程见步骤1~步骤29;最后选择最优特征子集的具体过程见步骤30~步骤34。
算法1FSKCA 算法
假设n为样本的个数,d为特征个数,则算法1的计算复杂度分析如下:步骤2~步骤5 初始化蜜源位置和个数的计算复杂度为O(n);步骤9 根据K-means聚类算法以蜜源为中心进行聚类划分,计算复杂度为O(ndk),步骤10 计算适应度函数值的复杂度为O(nk),则步骤8~步骤15 引领蜂进行邻域搜索的计算复杂度为O(ndk)×O(Pop)×O(nk)。步骤17~步骤20 跟随蜂根据轮盘赌原则选择引领蜂的计算复杂度为O(Pop)×O(nk)。于是,步骤7~步骤28 总的计算复杂度为O(MAX×Pop×n2dk2);步骤32 计算特征区分度的复杂度为O(n2d),计算特征代表性的复杂度为O(n2),计算特征重要度值并根据特征重要度值进行排序的计算复杂度为O(dlbd),其中最大更新次数MAX、Pop和k为常量。由于MAX、Pop和k均为常量,与n和d存在巨大的数据量差异,且常数可以忽略不记,因而FSKCA 算法总的计算复杂度为O(n2d)。另外,相关的比较算法的计算复杂度分析如下:MCFS(multi-cluster feature selection)[28]算法的计算复杂度为O(n2d+km3+nkm2+dlbd),其中m表示所选择特征子集个数,k表示聚类簇数目;LLCFS(local learning based clustering feature selection)[29]算法的计算复杂度为O(n3);UDFS(unsupervised discriminative feature selection)[30]算法的复杂度为O(d3) ;SPFS(spectral feature selection)[31]算法的复杂度为O(dn2);EUFSFC(efficient unsupervised feature selection method based on feature clustering)[32]算法的计算复杂度为O(d2)。总之,FSKCA 算法的计算复杂度略高于EUFSFC 算法[32],略低于LLCFS 算法[29]和UDFS 算法[30],接近于MCFS 算法[28]和SPFS 算法[31]。
为了方便读者更好地理解FSKCA 算法,以鸾尾花卉数据集Iris 为例来进行解释。首先,从Iris 数据集中随机选取50 个样本作为蜜源,初始化算法最大迭代次数500,蜜源最大迭代次数20,计算Iris 数据集中的各个蜜源的适应度值,并按照从大到小的顺序排列,前一半设置为引领蜂,后一半设置为跟随蜂。在引领蜂阶段,搜索最佳蜜源并更新。在跟随蜂阶段,跟随蜂根据轮盘赌原则选择引领蜂,选择完成后对Iris 数据集进行K-means 聚类,更新得到新的聚类中心,用新的聚类中心再更新蜂群。如果引领蜂迭代20 次后位置没有变化,引领蜂变为侦察蜂,随机选取蜜源进行更新。重复上述步骤直到达到最大迭代次数500,输出Iris 数据集完成聚类的3 个簇。其次,计算Iris 数据集中3 个簇各特征的特征区分度与特征代表性。最后,计算特征重要度,选出特征重要度最大的3 个特征作为最优特征子集输出,则算法结束。
3 实验结果与分析
3.1 IABC 算法的优化性能分析
本节从文献[19]中选择9 种基准测试函数对IABC 算法与PSO 算法[17]、ABC 算法[13]、结合食物源位置更新的ABC 算法(ABC algorithm combined with food source location update,ABCL)[27]、结合邻域搜索范围动态调整的ABC 算法(ABC algorithm combined with dynamic adjustment of neighborhood search range,ABCC)[20]、IABC1 算法(结合2.2 节中定义5 邻域搜索策略的ABC 算法)、IABC2 算法(结合2.1 节中定义3新的适应度函数策略的ABC 算法)进行优化性能测试。其中f1~f5为单峰函数,主要测试算法的寻优精度;f6~f9为多峰函数,具有多个局部最优点,通常检验算法的全局搜索性能和避免局部收敛能力。为了保证实验的公正性,在50 维和100 维上设置最大迭代次数分别为500 和1 000,种群数量为50。为了防止随机实验影响算法的评估,每种算法均独立运行30 次。9 种基准测试函数在2 种不同维度的运行结果如表1 所示,使用最优值(best)、最差值(worst)、平均值(mean)和标准差(std)来评价算法优化性能,其中mean和std越小表明算法的搜索能力和稳定性越好。实验硬件配置为Windows10 操作系统、16.00 GB RAM 和Intel®1.60 GHz CPU,软件为MatlabR2016b,实验结果表中粗体表示最优结果。
从表1 中的50 维测试结果可知,在f1~f6、f9这7个函数上,IABC 的4 个指标值均最优;IABC1 的4 个指标值均优于ABCL 和ABCC;IABC2 的4 个指标值在f4~f6、f9函数上均优于ABC,在f1~f3函数上的std值比ABC 差,但它的best、worst和mean优于ABC。在f7~f8函数上,IABC 在best、worst和mean上明显最优,在std上略差于IABC1,但优于其余算法;IABC1 在4 个指标值均优于ABCL 和ABCC;IABC2的std值 比ABC 差,但 在best、worst和mean优 于ABC。由100 维上的实验结果可知,在f3~f5和f7~f9这6 个函数上,IABC 的best、worst、mean和std均最优;IABC1 在f3~f5和f7、f9函数上的4 个指标均优于ABCL 和ABCC,在f8函数上std值略低于ABCC,但best、worst和mean表现最优;IABC2 在这6 个函数上的4 个指标值均优于ABC。在f1函数上,IABC 的stdIABC1 在4 个指标上的运行结果均优于ABCL 和ABCC;IABC2在这4个指标上运行结果均优于ABC。在f2函数上,IABC 的best略低于IABC1,但worst、mean和std均高于其余算法;IABC1在4个指标上的运行结果均优于ABCL和ABCC;IABC2在这4个指标上运行结果均优于ABC。在f6函数上,IABC 的worst略低于IABC1,但best、mean和std高于其余算法;IABC1 在4 个指标上的运行结果均优于ABCL 和ABCC;IABC2 的std略低于ABC,在best、mean和worst上与ABC相同。
为了从消融实验角度分析算法性能,依据表1中IABC、IABC1 和IABC2 这3 种算法的实验结果,进一步分析并突出改进算法的优势。在50 维上,在f1~f6、f9这7 个函数上关于4 个指标的运行结果IABC 均优于IABC1 和IABC2 算法;在f7函数上,IABC 的std略低 于IABC1,但高于IABC2,同时,IABC 的best、worst和mean均高于IABC1 和IABC2;在f8函数上,IABC 的std略低于IABC1 和IABC2,但IABC 的best、worst和mean均高于IABC1与IABC2。在100 维上,f3~f5和f7~f9这6 个函数上关于4 个指标的运行结果,IABC 均优于IABC1 和IABC2 算法;在f1函数上,IABC 的std略低于IABC1,但高于IABC2,同时,IABC 的best、worst和mean均高于IABC1 与IABC2;在f6函数上,IABC 的best略低于IABC1,但高于IABC2,同时,IABC 的worst、mean和std均高于IABC1 与IABC2。从表1 的9 个测试函数实验结果看出,IABC 在50维的7个函数上表现最佳,在100维的6个函数上表现最佳。相比于IABC1和IABC2,结合IABC1 和IABC2 之后的IABC 的优化性能在各测试函数上均有所提升,特别是在50 维的f1~f6和f9,100 维的f3~f5和f7~f9,IABC 都较IABC1 和IABC2 有所提升,在其他测试函数上,这3 种算法的寻优精度相当。综上分析可知,IABC 中各策略的改进效果良好,但所有策略组合的性能是最佳的。
从表1 测试结果可知,在选择的9 个基准测试函数上,IABC 相对于其余6 种算法具备良好的优化性能,充分证明了IABC 的普适性。但是IABC 在这9个函数上的4 个指标上表现不是全优,究其原因是:IABC 一方面通过自适应概率表达式提高了最佳蜜源被选择的概率,另一方面对蜂群邻域搜索范围进行动态调整,提升了IABC 寻优能力。尽管这些策略有效提升了IABC 在处理单峰和多峰函数时的寻优精度和收敛能力,但也会在一定程度上减弱其自身的全局搜索能力。总的来说,IABC 不仅在单峰函数上具有较好的寻优能力,而且在多峰函数上显示了更好的全局搜索能力。因而对ABC 的改进是有效可行的。
为了更清楚地说明IABC的收敛性能,以50维函数为代表性来展示上述7种算法的收敛曲线图(如图1 所示)。从图1 可以直观看出,IABC 在9 个基准函数上优化的收敛速度均领先于其他6 种对比算法。总的来说,IABC 在50 维9 个基准测试函数上的收敛性能是最优的。综合表1 和图1 来看,IABC 在函数优化的问题上表现较优,不仅收敛速度快,而且结果相比其余6 种算法更加优秀。因此,对ABC 的改进是切实有效的。
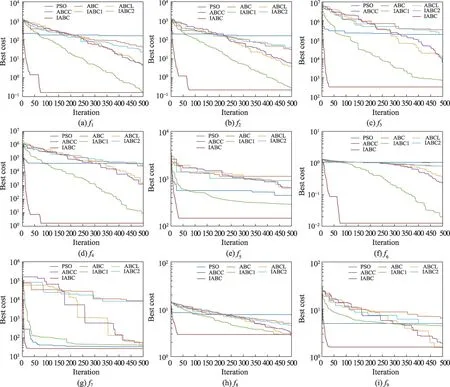
图1 7种算法在9个基准函数上的收敛曲线(维度为50)Fig.1 Convergence curves of 7 algorithms on 9 benchmark functions(50 dimensions)
3.2 IABCK算法的聚类分析结果
为了验证IABCK算法在不同数据集上的聚类分析效果,本节首先在7个合成数据集上对IABCK算法与K均值聚类算法(K-means)[4]、近邻传播算法(affinity propagation algorithm,AP)[33]、基于密度的含噪声空间数据库聚类发现算法(density-based algorithm for discovering clusters in large spatial databases with noise,DBSCAN)[34]、排序点识别聚类结构算法(ordering points to identify clustering structure algorithm,OPTICS)[35]、基于优化初始聚类中心和轮廓系数的K-means聚类算法(K-means clustering algorithm using optimal initial clustering center and contour coefficient,KCOIC)[36]进行对比分析。这7 种合成数据集(http://cs.uef.fi/sipu/datasets)的具体信息描述可见文献[36]。参照文献[36],选用4 个指标:调整互信息(adjusted mutual information,AMI)、归一化互信息(normalized mutual information,NMI)、兰德系数(Rand index,RI)和调整兰德系数(adjusted Rand index,ARI)。具体实验结果见表2 所示。为了更直观地说明这些算法的聚类性能,考虑到版面空间受限,仅在3 个代表性合成数据集上给出K-means、AP、DBSCAN、OPTICS、KCOIC 和IABCK 这6 种算法的聚类效果图,如图2至图4所示,其中不同的颜色代表不同 的簇。

图2 6种算法在Flame数据集上的聚类效果Fig.2 Clustering effect of 6 algorithms on Flame dataset

表2 6种算法在7个合成数据集上的实验结果Table 2 Experimental results of 6 algorithms on 7 synthesis datasets
由表2 可以得出:在Zelnik3、Aggregation 和R15这3 个数据集上,IABCK 在这4 个指标上的运行结果均优于其他5种对比算法,分别高出0.011 6~0.419 3、0.021 5~0.309 1、0.007 7~0.211 9 和0.010 3~0.507 4;在Flame数据集上,IABCK 在AMI和ARI指标上达到次优,其原因在于IABCK 对于形状复杂的簇识别能力相比KCOIC 较弱,但在NMI和RI指标上优于其他5 种算法;在Compound 数据集上,IABCK 在NMI、RI和ARI指标上低于最优的DBSCAN,其原因在于IABCK 在该数据集上未能实现正确的聚类划分,但在AMI指标上运行效果最佳;在Path-based 数据集上,IABCK 在AMI和ARI指标上略低于KCOIC,在NMI和RI指标上仅低于最佳的DBSCAN,达到了次优,究其原因在于IABCK 在处理一些簇边界难以分类的样本时效果并不优异,但优于另外5 种算法;在Jain 数据集上,IABCK 在AMI和ARI指标上次优,究其原因在于IABCK对于簇间密度差别较大的数据集聚类效果次于KCOIC,但在NMI和RI指标上达到最优。总的来说,在7种合成数据集上,IABCK在AMI、NMI、RI和ARI这4个指标下的表现效果优异。
如图2的实验结果所示,对于簇间没有明确界限的Flame 数据集,K-means、OPTICS 和IABCK 这3种算法均得到了正确的聚类结果,其余3种算法对于形状复杂的簇识别能力较弱。如图3所示,对于簇间密度差别较大的Jain 数据集,K-means、OPTICS 和IABCK这3种算法均实现了正确的聚类划分,而其他3 种算法在对簇间密度差别较大的数据集进行聚类时效果并不优异,究其原因是这3种聚类算法未能有效聚类簇间密度差别较大的数据集。如图4所示,对于簇间联系时而紧密时而疏松的R15 数据集,IABCK相比其他5种对比算法聚类效果最优,实现了正确的聚类划分,这表明IABCK 善于处理簇间时而紧密时而疏松的数据集。

图3 6种算法在Jain数据集上的聚类效果Fig.3 Clustering effect of 6 algorithms on Jain dataset
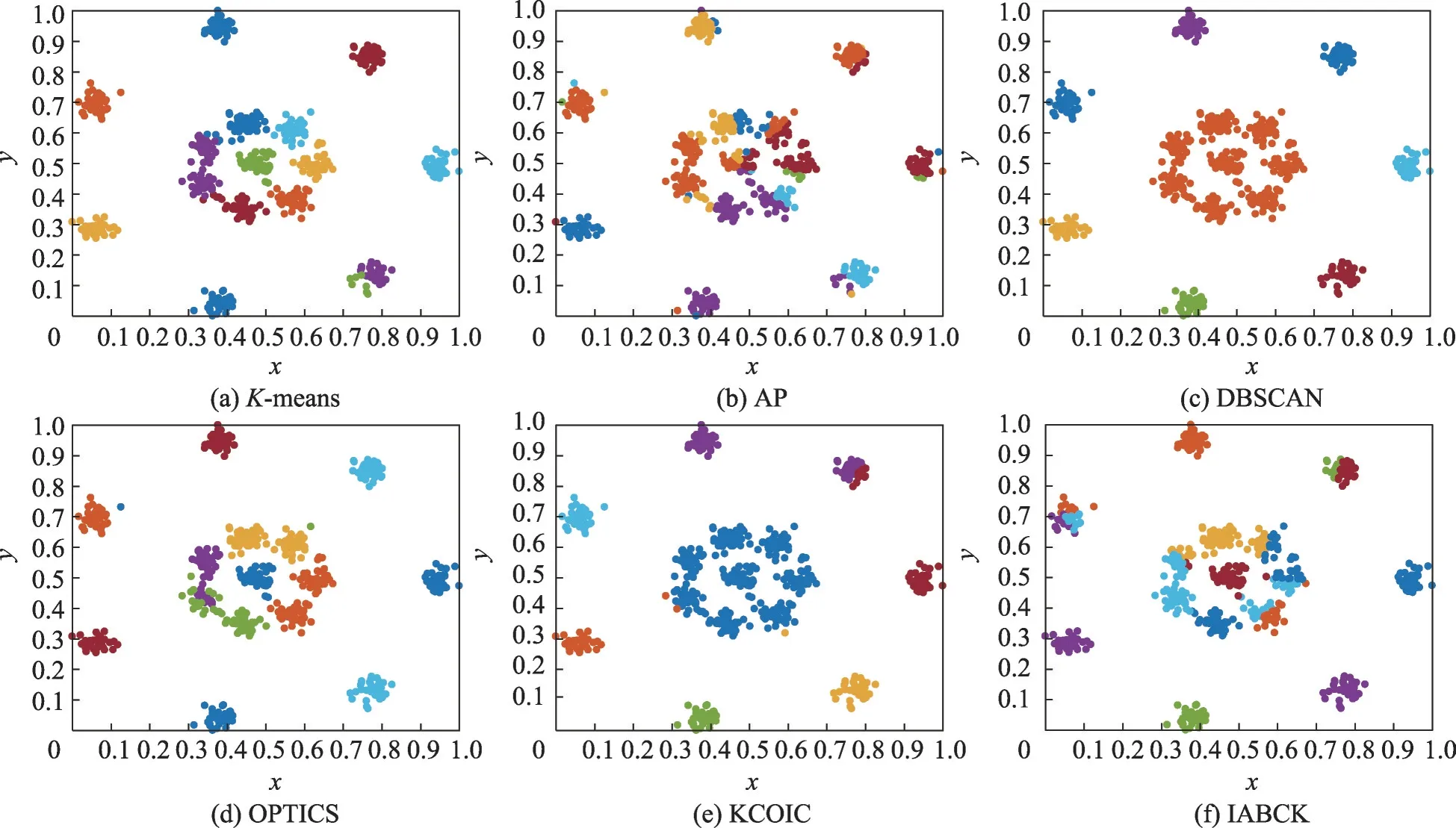
图4 6种算法在R15数据集上的聚类效果Fig.4 Clustering effect of 6 algorithms on R15 dataset
本节第二部分是在10个UCI数据集上将IABCK算法与6 种结合K-means 聚类的群智能优化算法进行实验比较,主要包括结合人工蜂群与K-means 聚类算法(ABC algorithm[13]combined withK-means[4],ABC+K-means)、结合粒子群与K-means 聚类(PSO algorithm[17]combined withK-means[4],PSO+K-means)、PAM(partial around medoids algorithm)[37]算法、自适应折叠混沌优化(adaptive iterative chaos optimization algorithm,GPAM)[38]算 法、CAABC+K-means 算 法(chaotic adaptive ABC algorithm[19]combined withK-means[4])和结合人工蜂群优化的粗糙K-means 聚类算法(rough ABC algorithm[15]combined withK-means[4],RABC+K-means)。这10 个UCI 数据集(http://www.ics.uci.edu)的具体信息描述可见文献[19]。参照文献[19],采用3 个评价指标:归一化互信息(NMI)、准确率(accuracy,ACC)和召回率(recall,R)。具体实验结果见表3。
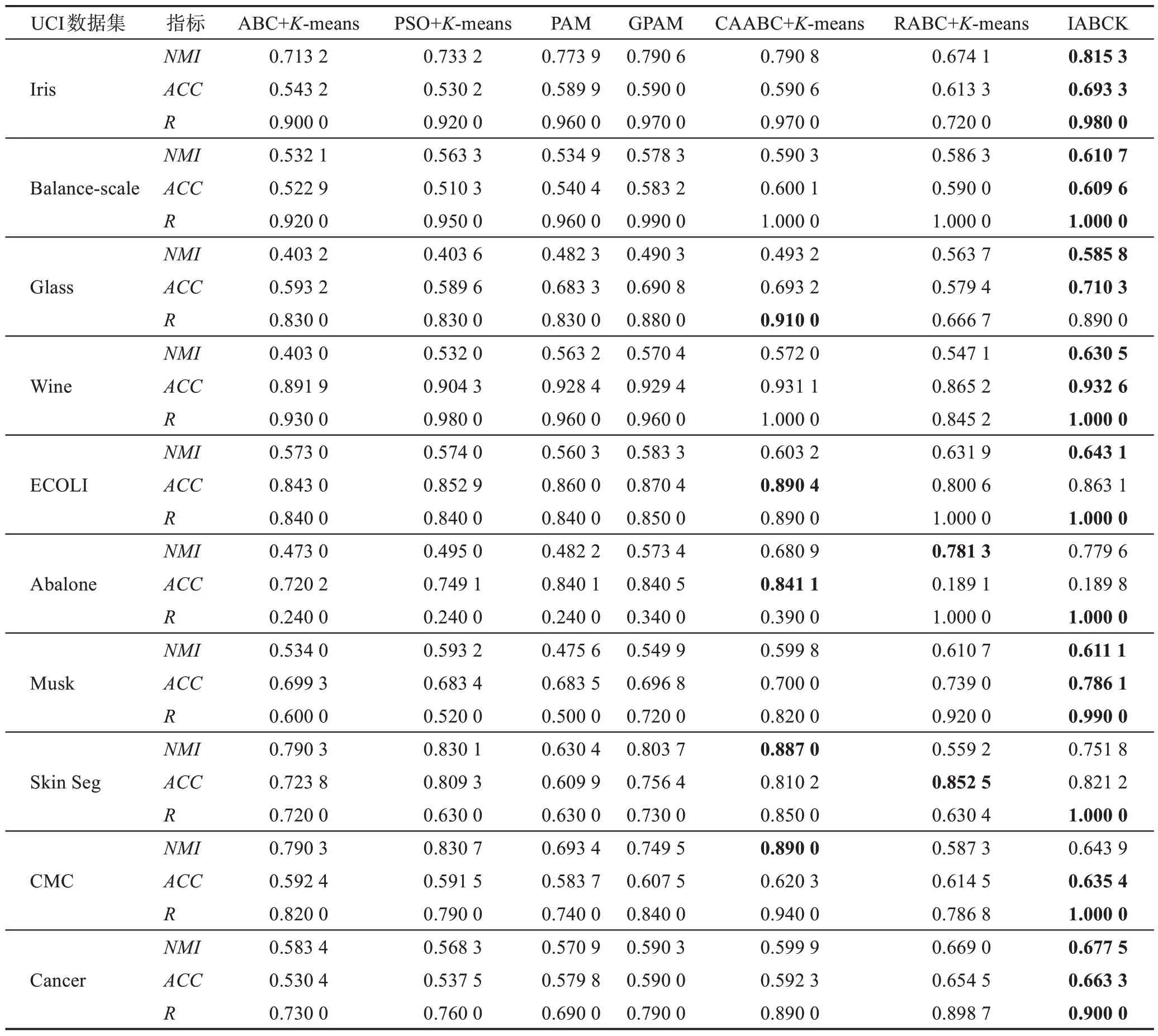
表3 7种算法在10个UCI数据集上的实验结果Table 3 Experimental results of 7 algorithms on 10 UCI datasets
由表3 可以得出:在Iris、Balance-scale、Wine、Musk 和Cancer 这5 个数据集上,IABCK 在3 个评价指标上的结果均优于6种对比算法,分别高出0.000 4~0.227 5、0.001 5~0.163 1 和0~0.490 0;在Glass 数据集上,IABCK 在R指标上的结果低于表现最佳的CAABC+K-means,究其原因在于IABCK 在聚类过程中对于真实情况下两个样本在同一个簇中,聚类后两个样本不在同一个簇中,但高出另外5 种算法0.010 0~0.223 3,同时该算法在NMI和ACC两个指标上的运行最优,分别高出其余算法0.022 1~0.182 6和0.017 1~0.130 9;在ECOLI 数据集上,IABCK 在ACC指标上低于表现最佳的CAABC+K-means,原因是CAABC+K-means 在该数据集上的聚类效果优于IABCK,但是在NMI和R指标上结果最优,分别高出其余算法0.011 2~0.082 8 和0.110 0~0.160 0;在Abalone和Skin Seg 数据集上,IABCK 在NMI和ACC指标上不是最优算法,究其原因是IABCK 在这2 个数据集上的聚类数目与真实情况存在差别,但R指标上的运行结果最优,优于其余算法0~0.760 0和0.150 0~0.370 0;在CMC 数据集上,IABCK 在NMI指标上的运行效果较差,究其原因在于IABCK 在该数据集上由聚类结果所得划分的熵值较小,但在ACC和R这两个指标上运行效果达到最优,分别高出其余算法0.015 1~0.051 7和0.060 0~0.260 0。总的来说,IABCK对于文中所选的10 个UCI 数据集在NMI、ACC和R这3 个指标上的运行效果优异。
3.3 FSKCA算法的特征选择结果
本节是在9 个UCI 数据集上对FSKCA 算法与文献[32]中 的LSFS、MCFS、LLCFS、UDFS、NDFS、SPFS、EUFSFC 这7 种算法以及文献[39]中的基于自适应邻域互信息与谱聚类的特征选择算法(feature selection algorithm based on adaptive neighborhood mutual information and spectral clustering,FSANS)进行比较。这9 个UCI 数据集(http://www.ics.uci.edu)的具体信息描述可见文献[32]。采用决策树(C4.5 decision tree,C4.5-DT)和多层感知器(multi-layer perceptron,MLP)这两种分类器,通过十折交叉验证计算特征子集诱导出来的分类精度,具体实验结果表现如表4所示。
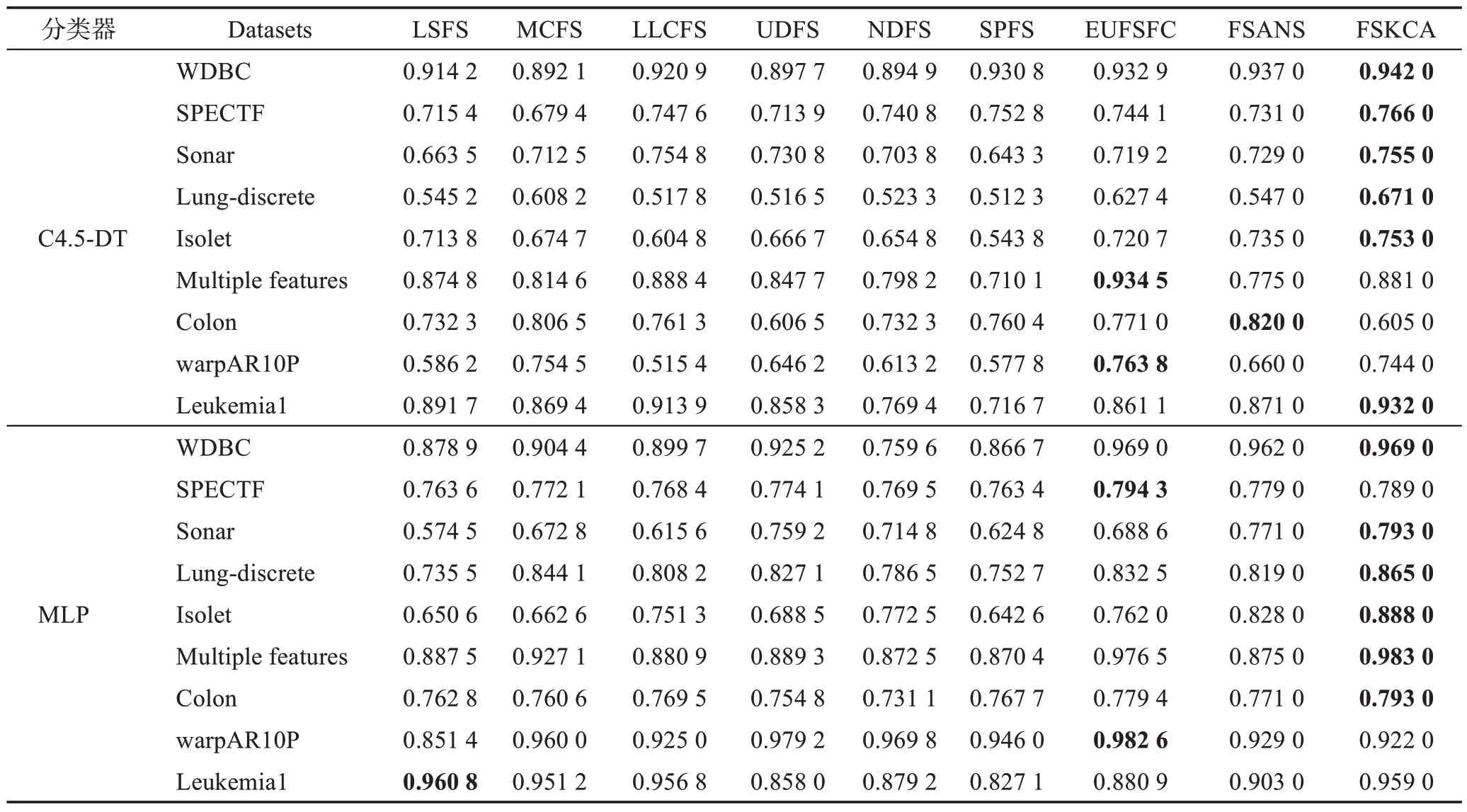
表4 9种特征选择算法在2种分类器上的分类精度Table 4 Classification accuracy of 9 feature selection algorithms on 2 classifiers
通过表4 的C4.5-DT 分类器的实验结果可以看出:在WDBC、SPECTF、Sonar、Lung-discrete、Isolet和Leukemia1这6个数据集上,FSKCA的分类精度达到最优,高出其余算法0.000 2~0.215 3;在Multiple features数据集上,FSKCA 的分类精度虽然低于LLCFS 和EUFSFC 这2 种算法,但高于另外6 种算法0.006 2~0.170 9;在Colon 数据集上,FSKCA 算法相比其余7种算法分类精度较差,但在warpAR10P 数据集上,FSKCA 的分类精度略低于MCFS 和EUFSFC 这2 种算法,但高于其他6 种算法0.097 8~0.228 6。FSKCA并未能在全部数据集上实现最优的分类精度,究其原因是:FSKCA 在Multiple features、Colon 和warpAR10P 这3 个数据集上未选择出具有最小冗余最大相关的最佳特征子集。在MLP 分类器下:在WDBC、Sonar、Lung-discrete、Isolet、Multiple features和Colon这6个数据集上,FSKCA 的分类精度均达到最优,优于其余算法;在SPECTF 数据集上,FSKCA的分类精度虽然比EUFSFC 低了0.005 3,但高于另外7 种算法0.010 0~0.025 6;在warpAR10P 数据集上,FSKCA 的分类精度不如最优的EUFSFC,但比LSFS 高0.070 6;在Leukemia1 数据集上,FSKCA 的分类精度仅比最优的LSFS 低了0.001 8,但优于其余7 种算法0.002 2~0.131 9。FSKCA 并未在全部数据集上关于MLP 分类器上实现最优的分类精度,原因在于:FSKCA 在SPECTF、warpAR10P 和Leukemia1这3 个数据集上未选择最优特征子集。总的来说,FSKCA 在C4.5-DT 和MLP 这2 种分类器下的9 个数据集的分类精度方面表现出很大的优势。
3.4 统计分析
为了评估对比算法的统计性能,采用Friedman检验和Nemenyi检验[1]进行测试。Friedman统计量表达式为:
其中,k表示算法的个数,N表示数据集的个数,Ri表示k个算法在N个数据集上的平均排名。如果平均距离水平超出临界距离,则两种算法性能将有显著差异。临界距离表达式为,其中qα表示临界列表值,α表示Nemenyi检验的重要度。
参照文献[1],使用CD图直观地显示比较算法之间的差异性,每个算法的性能平均排名沿轴绘制,最好的排名值在轴的左侧;当2种算法平均排名在一个误差之内时,用粗线将它们连接起来;否则认为它们之间具有显著的差异。依据表4中的分类精度结果,表5给出了9种特征选择算法在2种分类器下的统计结果,相应的CD图如图5 所示。在显著水平α=0.1时,qα=2.45,CD=2.83,其中k=9且N=9。通过以上实验可以看出,FSKCA 算法明显优于其他8 种算法,在统计分析方面表现出更好的优势,并且表现出较优的泛化性能。
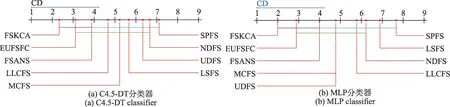
图5 9种算法在2种分类器下Nemenyi测试结果Fig.5 Nemenyi test results of 9 algorithms under 2 classifiers

表5 9种特征选择算法在2种分类器下的统计结果Table 5 Statistical results of 9 feature selection algorithms under 2 classifiers
4 结束语
本文提出了一种结合人工蜂群与K-means聚类算法的特征选择方法。首先,引入权重,改进了食物源的位置更新表达式,增强了人工蜂群的局部寻优能力;设计了同时考虑簇间和簇内性质的适应度函数,以使其计算更加合理。然后,构造了同时考虑样本之间相似性和特征之间的差异性的混合欧氏距离,解决了K-means 算法在进行距离计算时将不同样本和不同特征之间的差异同等对待问题。最后,设计特征重要度的表达式,用特征重要度来衡量特征,以选取最优特征子集。在9个基准函数上验证了IABC 算法的优化性能;在7 个合成数据集和10 个UCI 数据集上验证了IABCK 算法能有效提高聚类的全局搜索能力和准确率;2 个分类器上9 个UCI 数据集的特征选择结果验证了FSKCA算法的有效性。但是,所提算法进行K-means 聚类时聚类数目未实现自适应计算得到,存在一定的偶然性。因此,在今后的研究工作中,在提高聚类精度的情况下实现自适应计算聚类数目,寻求更加高效的聚类效果。
