基于复合模糊PID的植保无人机变量喷雾系统设计

罗明达,邓继忠,霍静朗,张建瓴,叶家杭,雷落成,张子超

(1.华南农业大学 工程学院,广州 510642;2.国家精准农业航空施药技术国际联合研究中心,广州 510642)

0 引言

农业航空精准作业是一项综合系统工程[1-4],而现阶段植保无人机在喷雾系统控制方面的研究相对较少[5-6]。近年来,随着植保无人机的快速发展及推广应用,国内研究机构陆续开展了植保无人机喷雾控制方面的研究。王玲[7]等设计了一款以PWM调制控制输出的无人机低空变量喷雾系统。王大帅等[8]设计了一种植保无人机动态变量施药系统,控制精度符合预期,但没有完全解决由于飞行速度变化导致的施药不均匀现象。岑振钊等[9]研发了一种基于神经网络PID的变量喷雾系统,试验表明:系统响应与设定值平均偏差为8.43%,为变量喷雾控制算法研究提供了参考。Wen[10]等进行了神经网络PID控制算法在植保无人机精准对靶施药方面的研究,发现喷雾系统从处方值信息变化到调整响应的调节时间控制在0.25s。刘洋洋等[11]提出了一种多信息融合的无人机变量施药的分级算法,可根据飞行参数变化自动调节施药流量,误差控制在10%内。

由上述研究可知:目前喷雾变量控制研究主要侧重于变量功能的实现,在喷雾流量随飞行速度变化自适应调整的精准控制方面仍有优化空间。为提升现有植保无人机喷雾流量随飞行速度变化自适应调整的精准性,降低施药偏差,笔者分析了PID与模糊PID控制方式的特点,并在结合两者优点、优化两者算法基础上,设计了一种基于复合模糊PID控制算法的植保无人机变量喷雾系统,进一步优化植保无人机喷雾现有控制系统响应的时效性、稳定性与精确性。根据植保无人机的飞行速度,通过控制算法调制PWM输出,实时调整变量喷雾系统喷雾流量,为精确施药提供可靠支持。

1 系统设计

变量喷雾系统主要由传感器模块、通信模块、喷雾输出模块以及配套的辅助功能模块组成,如图1所示。其中,STM32F407VET6单片机为系统处理器,主工作频率为168MHz,FLASH与RAM空间大小分别为512KB和192KB,满足现阶段主流控制算法如PID算法的计算要求;RTK(Real Time Kinematic)模块采用厘米级G-RTK实时定位定向系统,用于传输定位、飞行速度等信息;无线通信功能通过ATK-LORA-02低功耗通讯模块实现;传感器模块包含流量传感器与电机测速传感器。流量传感器型号为YF-S401,工作电压范围4.5～24V,测量范围为0.5～5.0L/min;隔膜泵的电机测速传感器采用AB相电机编码器,工作电压5V,嵌合STM32系列单片机的编码器计数模式,可显著降低检测误差;电机驱动模块采用EG2104S模块,系统采用双驱动模块,可分别独立驱动两个隔膜泵,控制PWM输出;隔膜泵型号为DP-521,额定电压为12V,额定功率为24W,最大压力为0.48MPa,可通过PWM调制控制输出功率;喷头为配套的压力式喷头。

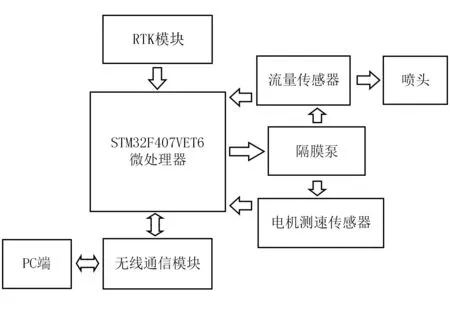
图1 变量喷雾系统原理框图Fig.1 Principle diagram of variable spray system

系统具体工作流程如下:单片机根据接收的施药任务与飞行速度参数推算PWM输出占空比,通过控制隔膜泵输出功率实现变量喷雾;通过传感器监测的数据,单片机实时比较目标流量与输出流量,并使用复合模糊PID控制算法校正偏差,实现喷雾流量精确控制。

2 控制算法分析与设计

2.1 PID控制算法分析

PID控制算法作为模糊PID控制算法的二次控制环节,同时作为本文设计算法的末端控制器,在控制算法的设计中具有十分重要的作用。传统PID控制规律表达式及其传递函数表达式[12]分别为

(1)

(2)

其中,Kp为PID的比例系数,影响系统响应的速度与静差;Ki为积分系数,影响系统响应的静差与超调量;Kd为微分系数,影响系统响应的速度与超调量。因此,PID参数的整定需要考虑三者对控制系统的响应性能影响。PID是现阶段控制执行机构采用最广泛的控制算法,可快速响应,使系统输出达到设定值允许的误差范围内,但其控制效果较大程度上依赖操作人员的经验[13]。本文阐述用以设计参照的控制系统均采用增量式PID控制算法,它是根据系统当前时刻控制量和上一时刻控制量的差值进行递推计算的误差校正算法,即

Δu(k)=Kp[e(k)-e(k-1)]+Kie(k)+

Kd[e(k)-2e(k-1)+e(k-2)]

(3)

根据PID参数特性,以水泵电机转速设定值与实际值的差值为偏差e,通过大量参数整定试验,确定Kp、Ki、Kd的参数分别为4、1.5、0.15时,基于PID控制的系统仿真阶跃响应调节时间较小,约为0.07s,如图2所示。系统响应无稳态误差,但超调量显著,约为33.3%。

图2 PID阶跃响应曲线Fig.2 Step response curve of PID

2.2 模糊PID控制算法分析

模糊PID控制器由模糊控制器及PID控制器结合而成,以误差e和误差变化率ec为模糊控制器的精确量输入并作模糊化处理;同时,依据模糊控制规则推算出对应的模糊量,解模糊推算整合输出结果作为PID控制器的增量参数ΔKp、ΔKi、ΔKd,与原始整定参数Kp0、Ki0、Kd0相加为最终的PID控制器整定参数,即Kp、Ki与Kd。

本文模糊PID算法中的模糊控制器输入值,即为e与ec分别为水泵电机转速偏差与偏差变化率;所构建PID控制器的原始整定参数(即Kp0、Ki0、Kd0与2.1小节中PID控制器的整定参数相同;构建的模糊控制器输入输出隶属函数模型采用的函数相同,分别为trimf和gaussmf两种函数,如图3所示。但是论域不同,E、EC、ΔKp、ΔKi,ΔKd论域分别为[-5,5],[-5,5],[-3,3],[-1,1],[-0.1,0.1],模糊集合均为{NB,NM,NS,ZE,PS,PM,PB}。制定的模糊规则如表1所示。

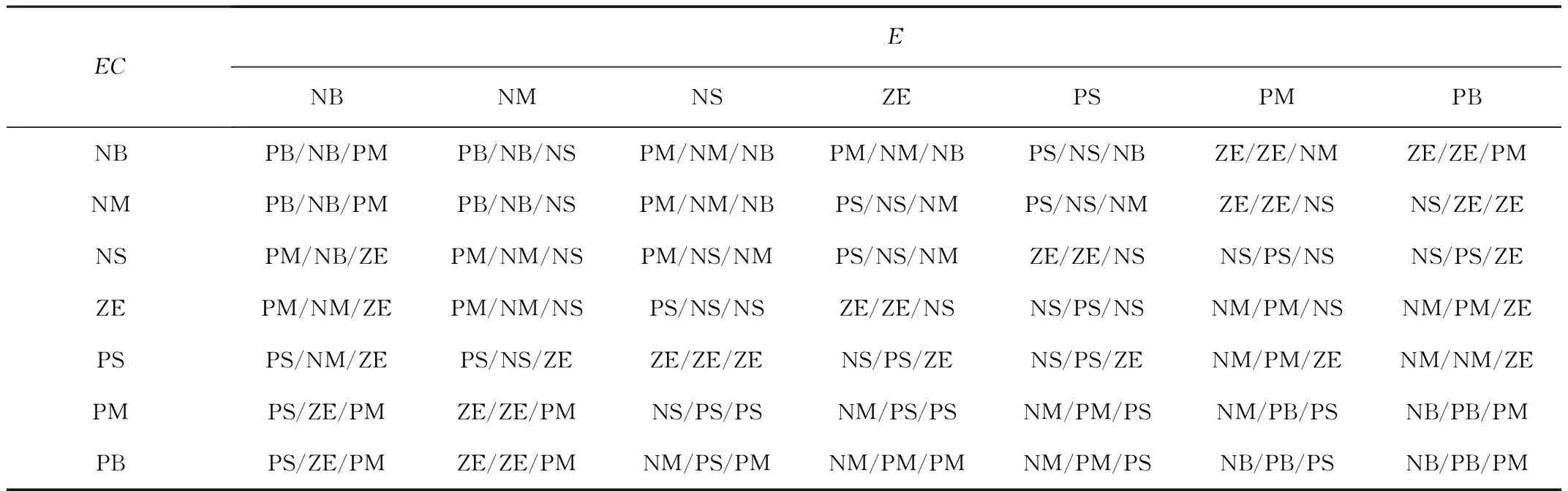
表1 ΔKp、ΔKi、ΔKd模糊规则表Table 1 Fuzzy rule table of ΔKp, ΔKi and ΔKd

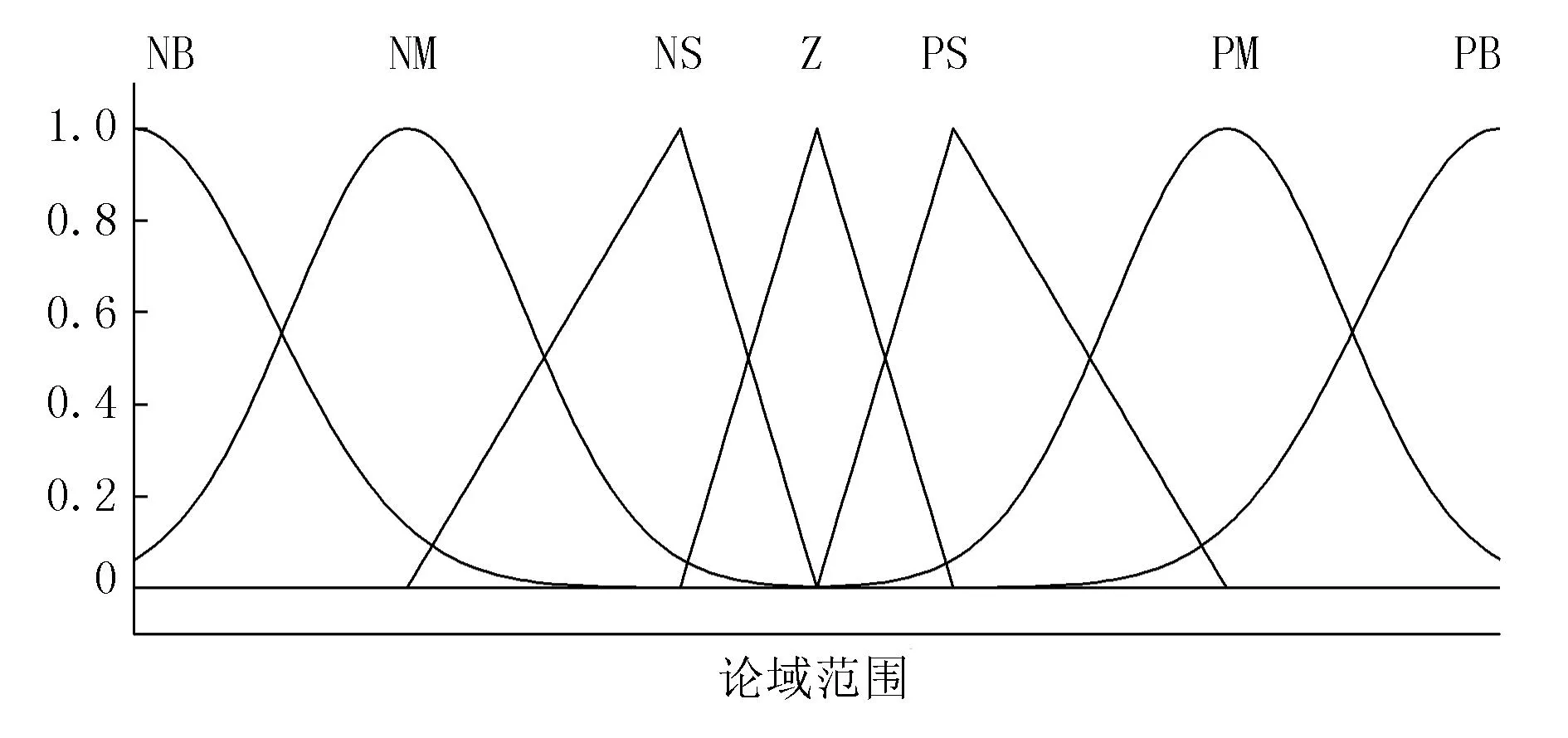
图3 隶属函数Fig.3 Mmembership function

系统的控制规则库是由若干条规则组成的,对每一条推理规则都可以得到相应的模糊关系,n条规则就有n个模糊关系。对系统的全部控制规则所对应的模糊关系进行并运算,可得总模糊关系矩阵R,即

(4)

其中,Rj表示表1控制规则中的第j条规则。

根据模糊推理规则[15],可得

Qij=(Ei·ECj)∘R

(5)

其中,Qij为模糊推理输出。

由此分别推算各模糊控制器输入输出关系,如图4所示。

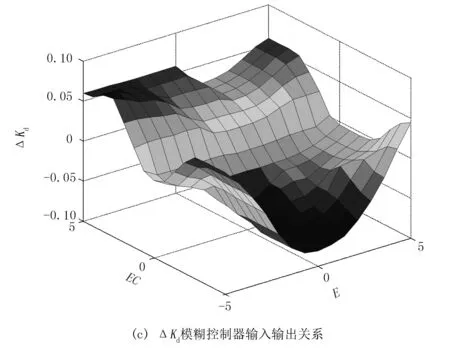
图4 各模糊控制器输入输出关系Fig.4 Input output relationship of each fuzzy controller

模糊PID的增量式PID控制器输入输出离散化表达公式与式(3)相同,阶段曲线如图5所示。由图5可知:与PID控制相比,基于模糊PID控制的系统仿真阶跃响应无超调量,解决了PID控制方式下超调量显著的缺陷;但调节时间较长,约为0.21s;系统响应无稳态误差。

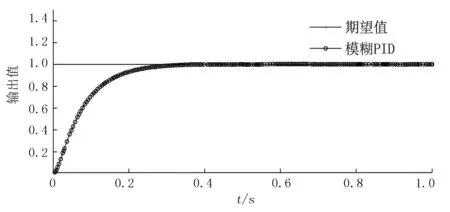
图5 模糊PID阶跃响应曲线Fig.5 Step response curve of fuzzy PID

2.3 复合模糊PID算法设计

由上述分析可知:PID控制存在超调量大的缺陷,模糊PID控制虽改善了PID控制存在的上述问题,但在响应速度方面仍有较大的优化空间。这主要是因为参数整定与控制规则制定较为依赖工程经验,较难同时兼顾各个指标,导致了实际响应效果的不理想。本文在控制算法方面研究的主要目的是设计一种较大程度同时兼具PID控制及模糊PID控制方式优点、又改善其显著缺陷的控制算法,故将PID与模糊PID结合,设计出复合模糊PID算法,优化了前二者的结构、降低开发难度的同时发挥良好的控制效果,一定程度上解决了PID与模糊PID参数整定与控制规则制定比较依赖工程经验的难题。通过对水泵电机转速设定值与实际值的偏差e进行绝对值化处理,即通过图6中的|u|模块生成偏差的绝对值|e|。当|e|高于设定的阈值时,使用PID算法控制;当|e|低于该阈值时,使用模糊PID算法控制,如此在偏差显著情况下系统响应速度快,相较于模糊PID再次缩短了响应时间。同时,在系统响应偏差较小时,切换为模糊PID控制,控制了超调量,发挥了模糊PID控制的优势。因此,将模糊PID控制与PID控制策略结合成一种新的复合控制策略,再次优化喷雾系统控制算法的总体性能。为此,通过大量调试确定复合模糊PID的算法切换阈值为电机转速设定值的10%时系统响应效果最佳。其算法流程如图7所示。

注:r为电机转速设定,y为电机转速实际值,e为设定值与实际值的偏差,ec为偏差变化率,|u|为绝对值化处理模块 ,|e|为偏差绝对值。图6 复合模糊PID算法框图Fig.6 Block diagram of compound fuzzy PID algorithm

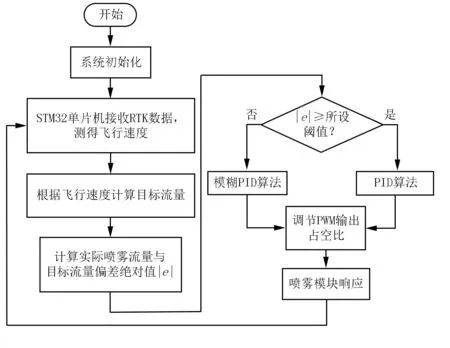
图7 复合模糊PID算法流程Fig.7 Flow chart of compound fuzzy PID algorithm

3 试验设计与结果分析

通过搭建测试平台,进行喷雾系统水泵电机转速与对应流量关系公式的拟合试验,以及变量喷雾系统控制算法响应速度、稳定性与精确性的对比试验和飞行速度与喷雾流量响应曲线跟踪试验,以此验证基于复合模糊PID控制的变量喷雾系统总体性能。喷雾系统测试平台如图8所示。

图8 喷雾系统测试平台Fig.8 Test platform for spray system

3.1 喷雾系统的测试数据

由于水泵电机转速与喷雾流量密切相关,为适应不同功率输出的电源,需得出精准喷雾流量对应的电机转速,并根据这种关系调整电机转速,从而实现对喷雾流量的精准控制。在此,进行了水泵电机转速与对应流量关系公式的拟合试验,即通过电机编码器检测水泵电机转速(单位r/s)对应的喷雾流量,并根据所得数据拟合对应的电机转速-流量公式。试验发现,根据电机编码器测量水泵电机转速推算的喷雾流量比流量传感器检测的精度更高。因此,在试验中以电机编码器进行喷雾流量的检测,以流量传感器为辅助校验工具。

在测试中发现电机转速小于10r/s时水泵无法抽出连续的水流,故以电机每秒转速区间[10,60]对应每1s量筒收集的流量体积来绘制水泵电机转速对应的喷雾流量曲线,如图9所示。

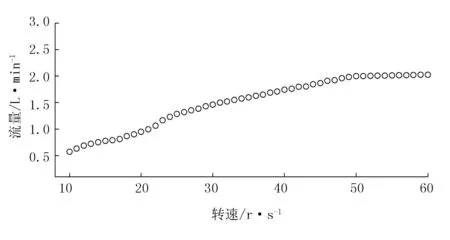
图9 水泵电机转速与实际喷雾流量关系Fig.9 Relationship between pump motor speed and actual spray flow rate

由图9可知:水泵电机转速与系统喷雾的流量体积不是线性关系,需要通过对数据进行拟合来求出二者的关系模型。由于水泵电机转速在50r/s之后的喷雾流量变化已不明显,且实际测试过程中水泵电机转速在25r/s时喷雾喷头才能达到稳定的雾化喷雾状态,故以电机转速在25～50r/s的响应数据为依据,对试验数据进行拟合优化。

转速区间在[25,50]的电机转速对应实际喷雾流量的关系如图10所示。通过线性回归拟合方程,得出的电机转速-流量公式为

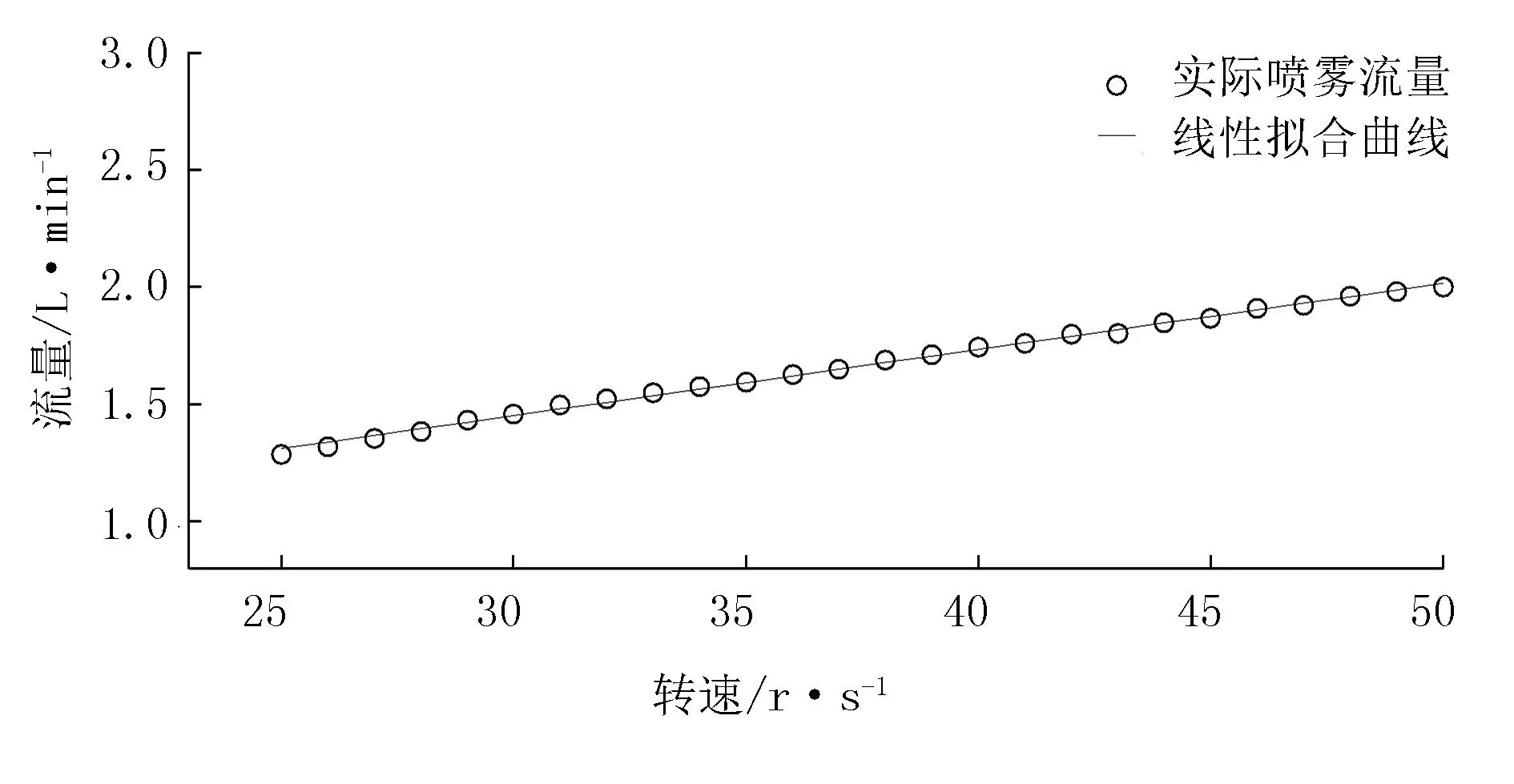
图10 电机转速25-50r/s对应的实际喷雾流量Fig.10 Actual flow rate corresponding to motor speed of 25-50r/s

Qyout2=0.0282x+0.6059

(6)

其中,Qyout2为转速区间在[25,50]单个水泵的实际喷雾流量(L/min);x为电机转速(r/s)。曲线拟合效果良好,决定系数R2=0.9973,实际流量与理论值的精度误差较低,最大误差1.56%,可为系统喷雾流量的精度控制提供准确计算值支持。

3.2 3种控制策略下的系统响应对比

测试搭载不同控制算法的喷雾系统响应的调节时间、超调量、进入稳定状态后的动态误差,将3种控制算法分别移植到基于STM32的系统中,算法移植后的程序最大占用STM32的ROM为34.25kB,占用率6.69%;RAM为10.87kB,占用率5.66%。因此,芯片选型满足系统计算需求。

各控制算法下喷雾系统响应情况对比如图11所示。由图11中可知:PID响应速度最快,在0.175s内达到响应要求,超调量较大,达到17.19%;喷雾系统初期不稳定状态较显著,且响应达到稳定输出后动态误差较大,最大误差达到4.688%;模糊PID无超调量,且响应达到稳定输出后动态误差相对PID显著降低,最大动态误差控制在3.125%内,但响应时间PID较长,达到了0.325s的响应时间范围;复合优化模糊PID响应速度相对模糊PID得到显著提高,调节时间缩短23.08%,控制在0.25s以内,符合植保无人机在高速作业条件下对施药系统反应速度的要求,且超调量相对PID降低63.64%,仅为6.25%。其响应达到稳定输出后的动态误差与模糊PID相同,最大动态误差均为3.125%,较大程度上兼具了PID及模糊PID的优势特点,如表2所示。

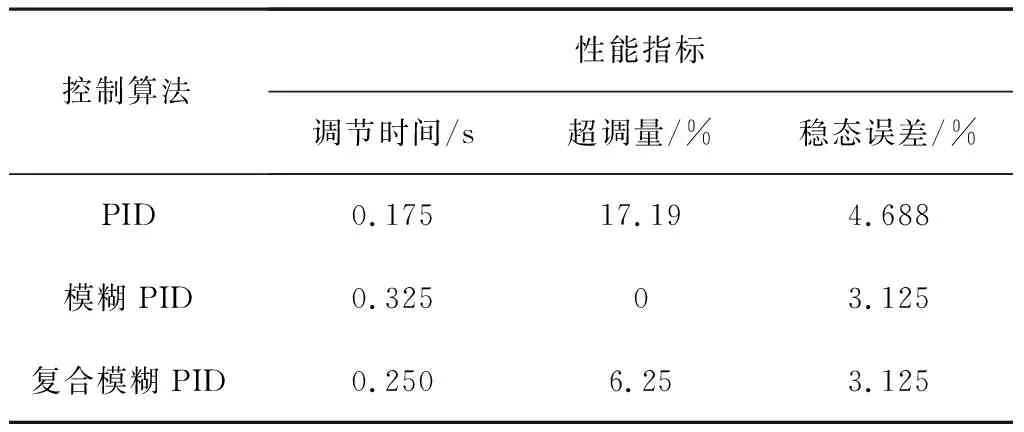
表2 喷雾系统响应的主要性能指标Table 2 Main performance indicators of spray system response

图11 各控制算法下喷雾系统响应情况对比Fig.11 Comparison of response of spray systems under different control algorithms

为验证对比不同控制算法喷雾系统喷雾流量的精准性,基于3种控制算法下的喷雾系统,搜集并对比每种控制算法下系统的电机每秒转速在区间[25,50]对应喷雾流量与理论值的偏差,如表3所示。

表3 水泵电机转速对应的理论喷雾流量Table 3 Theoretical spray flow corresponding to pump motor speed

由表4可推算PID、模糊PID与复合模糊PID单位时间喷雾流量的平均偏差分别为2.67%、3.85%、1.90%。PID算法下,系统实际喷雾流量总体上大于理论值,最大偏差达到4.01%;模糊PID总体误差与PID相比较大,且控制算法的响应速度较慢,水泵电机各转速对应的实际喷雾流量均未能达到理论值水平,最大偏差为-4.75%;与前二者的控制方式相比较,复合模糊PID控制方式下的喷雾系统实际喷雾流量除了水泵电机转速为25r/s时小于理论值、偏差为-3.70%外,其余转速下的喷雾流量偏差在三者中均为最小,总体满足植保无人机常规喷雾作业精准度的要求。

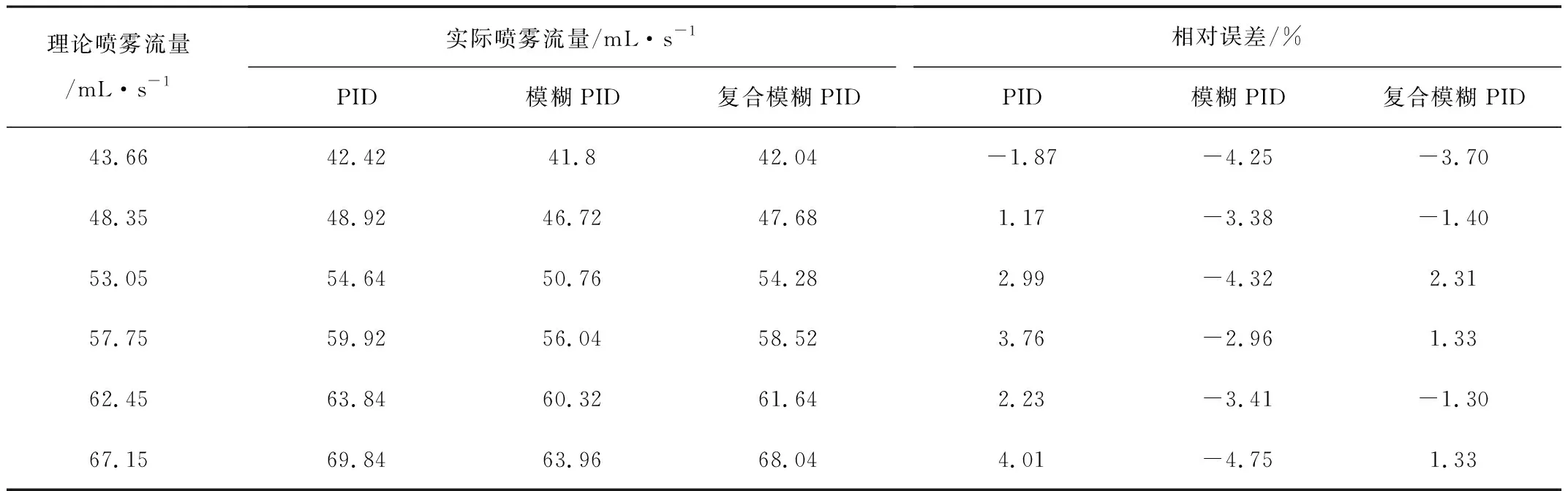
表4 单位时间内各控制算法响应情况Table 4 Response of each control algorithm in unit time

3.3 飞行速度与喷雾流量响应曲线跟踪

设定植保无人机作业速度在2.5～4m/s的区间变化,通过比例关系将无人机的飞行速度与变量喷雾系统的响应输出对应起来,变量喷雾系统根据飞行速度变化,实时调整喷雾流量。同时,变量喷雾系统将作业数据实时传回PC端,以此分析变量喷雾系统随飞行速度实时调节喷雾的实际情况。

飞行速度对应的喷雾流量如图12所示。由图12可知:基于复合模糊PID的变量喷雾系统在实际测试中的飞行速度与喷雾流量呈现出正比的关系,最大执行偏差为6.23%,关联程度较强。

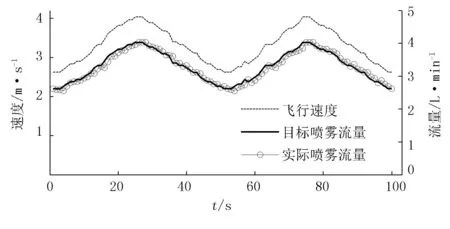
图12 飞行速度对应的喷雾流量Fig.12 Spray flow corresponding to flight speed

4 结论

1)平台测试表明:基于复合模糊PID的喷雾系统较模糊PID调节时间缩减23.08%,较PID超调量降低63.64%;稳态误差与模糊PID相同,控制在3.125%内,小于PID的4.688%;设定水泵电机每秒转速区间在[25,50]的情况下喷雾稳定性较好,实际喷雾流量与理论值偏差控制在3.33%以内,优于PID算法的4.27%及模糊PID算法的4.51%。

2)平台测试中,测得基于复合模糊PID算法的变量喷雾系统随飞行速度实时调整的实际喷雾流量与目标喷雾流量的最大执行偏差为6.23%,关联程度较强。

3)研究结果表明:复合模糊PID算法较大程度具备PID响应速度快的优势,同时改善了PID控制超调量显著、模糊PID调节时间长等缺陷,在降低开发难度的同时发挥了良好的控制效果,一定程度上解决了PID与模糊PID参数整定与控制规则制定比较依赖工程经验的难题。