非均质断层破碎带盾构开挖面极限支护力上限解*
2024-01-11廖伯富黄永杰许佳佳
廖伯富 黄 明 路 遥 黄永杰 许佳佳
(①福州大学,土木工程学院,福州 350116,中国)(②中铁十七局集团第六工程有限公司,福州 350014,中国)
0 引 言
盾构隧道施工中不可避免地会穿越断层破碎带,如福州滨海快线祥谦站-莲花山站区间盾构施工穿越大象山隧道、枕峰山隧道、岱岭隧道时均遇到断层破碎带。在断层破碎带中施工容易遇到突水涌泥、大变形、塌方等各种复杂问题(李志厚等,2008; 肖洋等,2018; 何发亮,2019; 周亚东等,2019; 兰恒星等,2021),其中最突出的就是隧道开挖面的稳定性问题(王林等,2020)。
针对盾构隧道穿越断层破碎带开挖面稳定性问题,郑泽源(2012)基于Horm掌子面稳定性分析模型和Janssen筒仓理论分析了跨江隧道穿越断层破碎带掌子面稳定性。Huang et al.(2019)基于强度折减法提出了组合滑楔稳定性分析模型用于评估跨断层水下隧道开挖面稳定性。王林等(2020)考虑完整岩体与断层破碎带交界面的影响,基于极限平衡理论研究了盾构隧道掘进过程中开挖面极限支护力的变化规律。杨建辉等(2021)采用MatDEM离散元软件模拟了隧道穿越断层破碎带时塌方全过程。张罗逊(2018)利用ABAQUS软件建立了隧道穿越富水断层破碎带的数值模型,分析了黏聚力、渗透系数等对掌子面稳定性的影响。他们在分析断层破碎带稳定性研究时都将断层破碎带简化成均质材料,这并不符合断层破碎带的非均质特性。事实上,断层由于经过长期的地质构造作用,破碎带内部不同部位承受的温度、压力及胶结程度各不相同,导致破碎带内部不同部位的力学性质存在较大差异,表现为高度的非均质性(付晓飞等,2005; 祝云华等,2009; 伍纯昊等,2021),同时,断层倾角的存在使得断层破碎带的非均质性沿非竖直方向变化,这促使隧道开挖面稳定性分析变得更加复杂,因此,如何精确合理地计算盾构在断层破碎带中施工时开挖面的支护压力成了盾构施工的一项关键技术。
极限分析上限法是分析隧道开挖面稳定的一种常用有效的方法(Davis et al.,1980; Leca et al.,1990; Mollon et al.,2009,2010a,2014; Zhang et al.,2019,2020a; 刘克奇等,2020; Wei et al.,2020)。近年来,越来越多学者将其用于分析盾构隧道穿越非均质地层时开挖面的稳定性研究,Pan et al.(2016)将三维破坏机制扩展到非均质土中隧道开挖面的稳定性分析,结果表明黏聚力随深度的线性变化的非均质性对临界面压力有显著影响。Zhong et al.(2020)认为非均质土的强度参数是在垂直方向上线性变化的,利用离散化技术研究了土体强度参数的非均质性对破坏形状和坍塌面积的影响。Li et al.(2020)基于对数螺旋的破坏机制提出了一种评估各向异性和非均质土中隧道工作面稳定性的新程序。Wilson et al.(2013)将土体不均匀性考虑到极限分析上下限有限元法中,分析了不同形状毛洞隧道不排水时开挖面的稳定性。Ukritchon et al.(2017)采用三维有限元分析了土体抗剪强度随深度线性增加的黏土不排水隧道开挖面稳定性。宋春霞等(2011)将多块体上限法用于纯黏土材料,推导了非均质地基中平面应变隧道极限支护压力的上限公式。他们针对土体水平分层的特性,将黏聚力考虑成随深度方向线性变化来体现土体的非均质性,分析了非均质性对隧道开挖面稳定性的影响。但是在断层破碎带中,构造运动的作用使得黏聚力的非均质性并非沿着竖直方向变化,而是沿着非竖直方向呈现非均质变化,在埋深相同位置不同处的黏聚力是不相等的,如果再采用黏聚力随深度线性变化的模型进行黏聚力等有关计算,得到的计算结果将与实际值存在一定误差,同时也会对开挖面稳定性分析产生影响。
综上分析,现有的非均质模型主要针对土层沿深度方向的非均质变化,不能充分反应断层破碎带非竖直方向的非均质性,无法应用于盾构隧道过断层破碎带开挖面稳定性研究。因此,亟需建立一种适用于断层破碎带的计算模型,用于确定盾构在非均质倾斜断层破碎带施工时开挖面的极限支护压力,确保盾构施工的安全。为此,本文引入非均质方向角和非均质系数角分别解决断层破碎带倾斜性、非均质性和非均质系数大小的问题,提出适用于断层破碎带的空间非均质分布函数模型。而后,将模型运用于盾构隧道开挖面极限支护压力的上限求解,通过算例和工程实例对该模型的正确性进行验证,详尽分析内摩擦角、初始黏聚力、隧道埋深比、非均质系数与非均质方向对隧道开挖面稳定性的影响,以此揭示断层破碎带的倾斜性与非均质性对开挖面稳定性产生影响的根本原因。研究结果为确定断层破碎带中盾构开挖面极限支护压力提供了一种可行的计算方法。
1 空间非均质分布函数模型
1.1 黏聚力沿深度线性变化模型分析
1.1.1 适用范围
黏聚力沿着深度方向线性变化,即:
c=cu0+ρy
(1)
式中:cu0为初始黏聚力;ρ为非均质系数。从式(1)可以看出黏聚力是关于埋深y的函数,只要埋深相同,黏聚力便相同,因此该模型仅仅适用于图1a非均质性沿深度方向变化的水平分层地层。而在图1b断层破碎带等非水平分层地层,黏聚力沿着非竖直方向线性变化,在埋深相同位置不同处的黏聚力不相同,这时黏聚力不再只是关于y的函数,无法再用式(1)计算黏聚力。
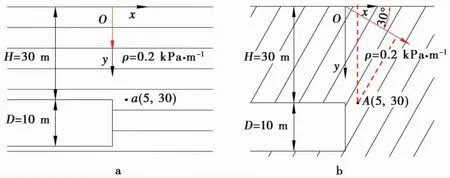
图1 非均质性沿着竖直和非竖直方向变化
1.1.2 产生计算误差
在断层破碎带中,黏聚力的非均质变化方向与竖直方向存在一定的夹角,此时采用式(1),即黏聚力随深度线性变化的模型进行计算,必然会产生误差。为了更加直观地描述出问题,列举简单的算例进行对比分析。
算例:图1b中,黏聚力的非均质性变化方向与x轴方向成30°夹角线性变化,假定非均质系数为ρ=0.2kPa·m-1,初始黏聚力为cu0=10kPa,坐标原点为O(0,0),计算A(5,30)处的黏聚力。
A处的实际黏聚力为:
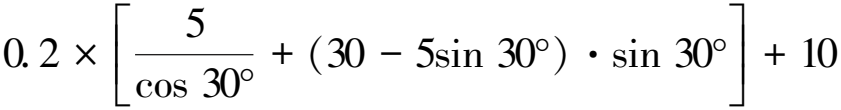
=13.87kPa
如果采用黏聚力随深度线性变化的模型进行计算,即式(1)计算,则:
c′A=ρHA+cu0=0.2×30+10=16kPa
其实c′A的计算结果实际为图1a中a(5,30)处的黏聚力ca。
A处黏聚力的相对误差:

借助上述简单算例分析可知,如果实际地层中黏聚力的非均质性沿着非竖直方变化,而仍然采用沿着竖直方向非均质性变化的模型进行计算,得到的计算结果将与实际值存在较大误差。
1.1.3 影响开挖面稳定性分析
Mollon et al.(2010a)认为开挖面的极限支护压力σt会随着黏聚力c的增大而减小。当用于计算的黏聚力大于实际黏聚力时,得到的极限支护压力计算值会小于实际值,导致极限支护压力被低估,存在风险隐患; 反之得到的极限支护压力计算值会大于实际值,导致极限支护压力被高估,如果在开挖面施加的压力过大,可能引起开挖面的被动破坏(Pan et al.,2016)。
1.2 空间非均质分布函数模型的建立
为降低断层破碎带中黏聚力等相关计算的误差,考虑断层破碎带的非均质性可能沿着竖直和非竖直方向变化,建立适用于断层破碎带的空间非均质分布函数模型。
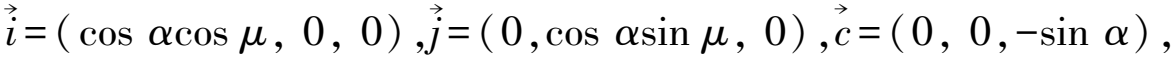
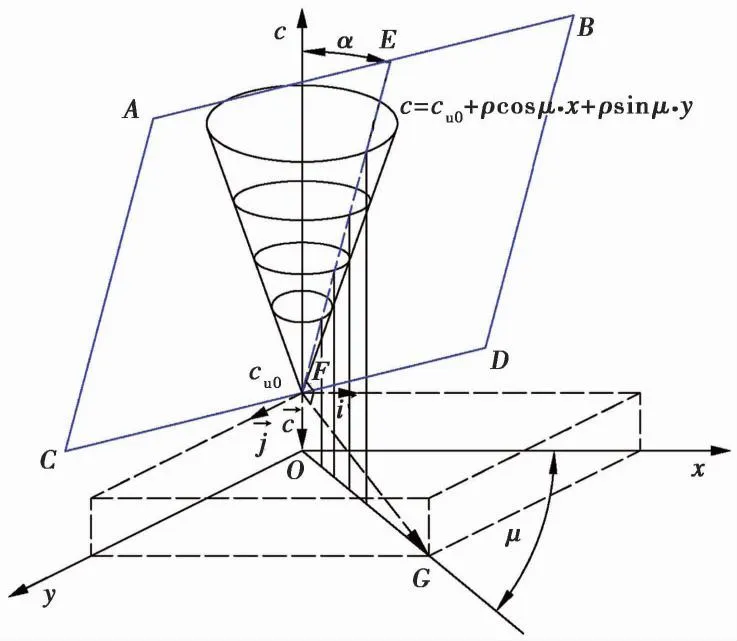
图2 空间非均质分布函数模型
cosαcosμ·x+cosαsinμ·y
+(-sinα)·(c-cu0)=0
(2)
化简得:
(3)

c=cu0+ρcosμ·x+ρsinμ·y
(4)
该模型主要由参数cu0、α、μ决定。式中,cu0为初始黏聚力,μ为非均质方向角,α为非均质系数角,ρ为非均质系数。
1.2.1 初始黏聚力cu0
通过引入参数cu0来确定破碎带初始黏聚力。
1.2.2 非均质方向角μ
通过引入非均质方向角μ来确定黏聚力非均质变化方向,解决黏聚力沿着任意方向非均质变化的问题,使模型满足断层破碎带的倾斜性和非均质性。平面ABCD通过绕圆锥旋转体现黏聚力可沿着任意方非均质变化,平面ABCD与圆锥的切线EF在xoy平面的投影为直线OG。直线OG的方向即为黏聚力非均质性变化方向,直线OG与x方向的夹角为非均质方向角μ,即黏聚力非均质性变化方向与x方向的夹角,并规定直线OG绕c轴顺时针旋转时与x轴形成的非均质方向角μ为正值,反之为负。
当非均质方向角μ=0°时,代入式(4)中可得:
c=cu0+ρx
(5)
式(5)表示黏聚力的非均质性沿水平方向变化,如图3a所示。
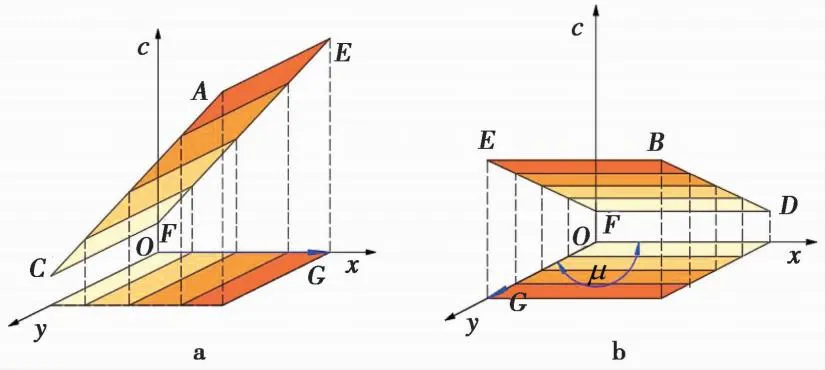
图3 非均质方向角与非均质方向的关系
当非均质方向角μ=90°时,代入式(4)中可得:
c=cu0+ρy
(6)
式(6)表示黏聚力的非均质性沿竖直方向变化,与式(1)相等,即黏聚力沿深度方向呈线性变化,如图3b所示。
在断层破碎带中,根据断层破碎带的结构特性可知非均质方向与断层面垂直,假定盾构上方断层面与x轴的交角为β,它与非均质方向角μ存在以下关系(图4):
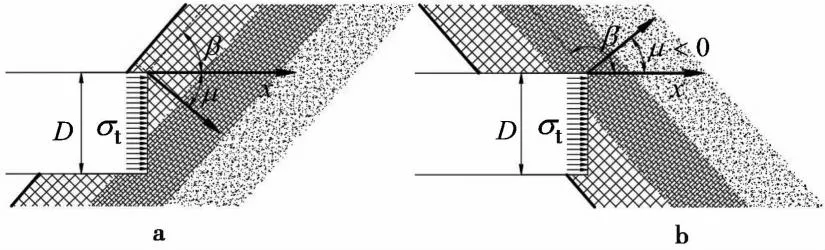
图4 非均质方向角与断层倾角的关系
β+μ=90°
(7)
1.2.3 非均质系数角α
通过引入非均质系数角α来确定黏聚力非均质变化比例系数,解决黏聚力非均质变化比例系数大小的问题。非均质系数角α为圆锥顶角,由数学几何知识可得,圆锥顶角α的余切值即为非均质系数的大小:
(8)
当0°<α<90°时,非均质系数ρ>0,黏聚力沿着非均质变化方向增大,如图5a。
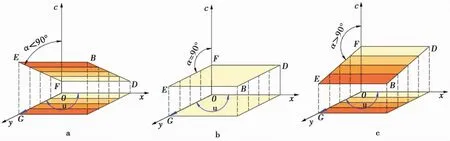
图5 非均质系数角与非均质系数的关系
当α=90°时,非均质系数ρ=0,代入式(4)得c=cu0,平面ABCD与xoy平面平行,空间平面内任何一点的黏聚力都是相等的,即为均质材料,如图5b。
当90°<α<180°时,非均质系数ρ<0,黏聚力沿着非均质变化方向减小,如图5c。
1.3 模型验证
(1)利用空间非均质分布函数计算图1a中a(5,30)点的黏聚力,非均质系数为ρ=0.2kPa·m-1,初始黏聚力为cu0=10kPa,非均质方向角μ=90°,代入式(4)得:
ca=10+0.2cos 90°×5+0.2sin 90°×30
=16kPa
(2)利用空间非均质分布函数计算图1b中A(5,30)点的黏聚力,非均质系数为ρ=0.2kPa·m-1,初始黏聚力为cu0=10kPa,非均质方向角μ=30°,代入式(4)得:
cA=10+0.2cos 30°×5+0.2sin 30°×30
=13.87kPa
通过对上述算例验算可知,黏聚力的非均质性沿着竖直方向和非竖直方向变化,采用空间非均质分布函数模型计算均能得到准确的结果,降低了断层破碎带中黏聚力等相关计算的误差,扩大了非均质性模型的适用范围。
2 盾构穿越断层破碎带开挖面稳定上限分析
应用极限分析上限定理分析隧道开挖面稳定性问题的求解步骤:首先是构建出与开挖面实际破坏情况相贴近的破坏模式,然后是分别求解出该破坏模式下的内能损耗率与外力功率,再根据虚功原理构建出内能损耗率与外力功率的等式求解得到目标函数,最后求解该目标函数在一定的约束条件下的最优上限解。
2.1 破坏模式的构建
Subrin et al.(2002)提出一种由空间对数螺旋面和隧道开挖面包络形成一个类似于“牛角状”破坏模型的开挖面破坏机制。Mollon et al.(2010b,2011)利用空间离散技术对Subrin提出的对数螺旋破坏模型进行了改进,分别得到了二维和三维对数破坏区,并运用极限分析上限定理研究了盾构隧道开挖面的稳定性。Senent et al.(2013)针对破碎岩体提出了以对数螺旋为界的破坏机制。该破坏机制涵盖了整个开挖面,通过案例测试和数值模拟验证了该破坏机制下计算得到的支护压力的合理性。Li et al.(2019)和Zhang et al.(2020b)针对风化饱和岩体和软岩体构建了3D旋转破坏机制。他们的研究成果表明以对数螺旋为界的旋转机制可以充分模拟破碎岩体破坏。基于上述分析,本文结合断层破碎带的工程特性,参照Senent et al.(2013)提出的破坏机制,建立适用于断层破碎带的双对数螺旋破坏模式。如图6所示,并将空间非均质分布函数模型应用于开挖面极限支护压力的求解分析。
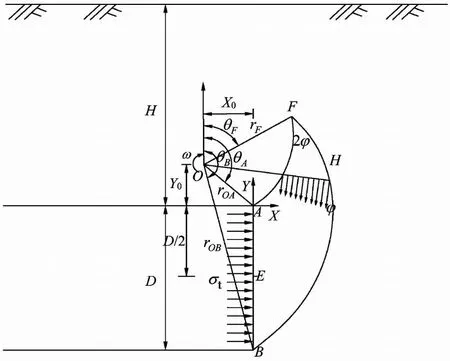
图6 断层破碎带中隧道开挖面平面应变破坏机制
如图6所示,断层破碎带中的破坏模式由对数螺旋线AF和BF组成,F点为两条螺旋线交点,A为XAY坐标系中的原点,(X0,Y0)为对数螺旋线的旋中心O点在XAY坐标系中的坐标,根据相关联流动法则可知,滑动面即速度间断面上相对速度的方向与其切线方向的夹角等于破碎带的内摩擦角,因此,对数螺旋线AF和BF的方程分别为:
rAF=rOAexp[(θA-θ)tanφ]
(9)
rBF=rOBexp[(θ-θB)tanφ]
(10)
式中:φ为破碎带的内摩擦角;θA为OA与Y轴的夹角;θB为OB与Y轴的夹角。
AB为隧道开挖面,E为AB的中点,隧道直径为D,埋深为H;OA、OB、OF、OE长度分别为rOA、rOB、rF、rE;OF、OE与Y轴夹角分别为θF、θE。根据几何关系可得:
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
2.2 外力功率的计算
构建出贴合实际的破坏模式后需计算满足该破坏模式下的外力功率、内能损耗率。本文外力功率做功主要为重力和支护压力所做功的功率。
2.2.1 重力功率的计算
对数螺旋线区域OBF的重度为γ,在重力作用下绕旋转中心O以恒定的角速度ω转动,由叠加法可知塌落体BAF在重力作用下所做的外力功率为:
WBAF=WOBF-WOAF-WOAB
(19)
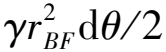
区域OBF内重力所做功率为:
(20)
区域OAF内重力所做功率为:
(21)
三角形区域OAB内重力所做功率为该区的塌落体重与该区重心速度的垂直分量乘积:
(22)
2.2.2 支护压力功率计算
假设在开挖面AB处的支护压力σt为均布形式,则支护压力做功为:
WT=-σtDrEωcos (π-θE)
(23)
所以,外力所做功率为:
W外=WOBF-WOAF-WOAB+WT
(24)
2.3 内能损耗率的计算
由图6可知,由于坐标轴原点建立在隧道拱顶位置,埋深为y=H,取地面位置的黏聚力为初始黏聚力cu0,根据式(4)可得在该坐标系下黏聚力空间非均质分布公式:
c=ρcosμ·x+ρsinμ×(H-y)+cu0
(25)
式中:cu0为初始黏聚力;μ为非均质方向角;ρ为非均质系数;H为埋深,y为某点距隧道顶面距离。
内部能量耗损发生在对数螺旋间断面AF与BF上,根据几何关系,由图6可知间断面AF与BF上的点在XAY坐标系中的坐标为:
xAF=rAFsinθ+X0
(26)
yAF=rAFcosθ+Y0
(27)
xBF=rBFsinθ+X0
(28)
yBF=rBFcosθ+Y0
(29)
将式(26)~式(29)代入式(25),得到间断面AF和BF上各点黏聚力随非均质方向变化的函数表达式为:
cAF=cu0+ρcosμ×(rAFsinθ+X0)
+ρsinμ×(H-rAFcosθ-Y0)
(30)
cBF=cu0+ρcosμ×(rBFsinθ+X0)
+ρsinμ×(H-rBFcosθ-Y0)
(31)
间断面AF上某微元的能量耗损率为该微元的微分面积rAFdθ/cosφ、黏聚力cAF、间断面的切向速度rAFωcosφ三者的乘积,间断面AF总的内部能量耗损可沿整个间断面进行积分:
(32)
同理,间断面BF耗损率为:
(33)
所以,双对数螺旋线破坏模式总的内部能量损耗功率为:
W内=WAF+WBF
(34)
2.4 极限支护压力上限解的求解
2.4.1 支护压力的上限解
根据上限定律中的虚功原理可知,构建的破坏模式需满足外力功率等于内能损耗率,则有:
W外=W内
(35)
将式(23)、式(24)、式(34)代入上式可得开挖面极限支护压力为:
(36)
根据前文的推导公式可知,WAF、WBF、WOBF、WOAF、WOAB、rE、θE均是X0、Y0的函数,所以支护压力σt也为X0、Y0的函数。
2.4.2 支护压力上限解的优化
本文中的破坏模式需满足的几何约束条件为:
rFcosθF+Y0≤H
(37)
通过MATLAB软件得到目标函数满足几何约束条件式(37)下的最优上限解。
3 工程实例验证与参数分析
3.1 工程实例验证
将空间非均质分布函数模型应用到广州地铁三号线大塘站到沥滘站区间发生地表塌陷事故(乔金丽,2009)分析,该区间采用土压平衡式盾构机施工,隧道直径为6m,盾构中心距地表为15m,如图7所示,该区间地层黏聚力沿深度方向减小。
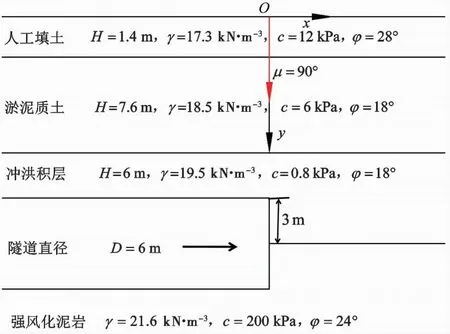
图7 地层剖面图
由图7可知,黏聚力非均质性沿竖直方向变化,即非均质方向角μ=90°,其余计算参数与梁桥等(2016)取相同的数据,ρ=-1kPa·m-1,cu0=12kPa,φ=18°,γ=18kN·m-3,H=12m,D=6m,得到计算结果如表1所示。

表1 开挖面支护压力比较
从表中可以看出,本文计算得到结果与梁桥等(2016)的计算结果几乎相等,两者计算误差小于1%; 从工程实例上验证了空间非均质分布函数的正确性和合理性,说明将空间非均质分布函数模型引入盾构穿越断层破碎带开挖面稳定性分析是可行的。
3.2 参数分析
根据式(7)断层破碎带与非均质方向角的关系可知,非均质方向角能够体现断层破碎带的倾斜性和非均质性对开挖面稳定性的影响。因此,分析过程中直接分析非均质方向角对开挖面稳定性的影响,实际工程中可以根据断层倾角与非均质方向角的关系进行换算得到断层破碎带对开挖面稳定性的影响。
参数选取区间:隧道埋深H=30m,盾构隧道直径D=8.5m,内摩擦角φ=15°~30°,γ=18kN·m-3,初始黏聚力cu0=5~20kPa,非均质系数ρ=-0.3~0.3kPa·m-1,非均质方向角μ=0°~90°。
3.2.1 非均质系数与非均质方向角对隧道开挖面极限支护压力的影响
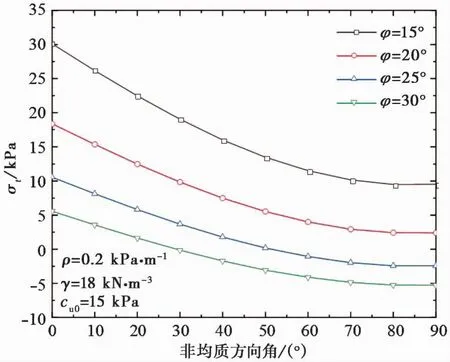
从图8中可以看出,开挖面支护压力在不同非均质系数ρ下随非均质方向角μ的变化曲线。非均质系数ρ=0,即非均质系数角α=90°时,非均质方向角μ的变化对隧道开挖面支护压力无影响,这是由于ρ=0时断层破碎带为均质材料,不论非均质方向角μ如何改变,开挖面前方破碎岩体性质均不变,盾构需提供的支护压力保持不变; 当非均质系数ρ<0,即非均质系数角90°<α<180°时,随非均质方向角μ的增大,开挖面支护压力增加,这是由于随着非均质方向角μ的增大,黏聚力由开始沿着水平方向减小慢慢变为沿埋深方向减小,降低了开挖面前方破碎岩体的黏聚力,破碎带的自稳能力减弱; 当非均质系数ρ>0,即非均质系数角0°<α<90°时,随非均质方向角μ的增大,开挖面支护压力减小,这是由于随着非均质方向角μ的增大,黏聚力由开始沿着水平方向增大慢慢变为沿埋深方向增大,提高了开挖面前方破碎岩体的黏聚力,破碎带的自稳能力增强。

图8 非均质方向角与非均质系数对支护压力的影响
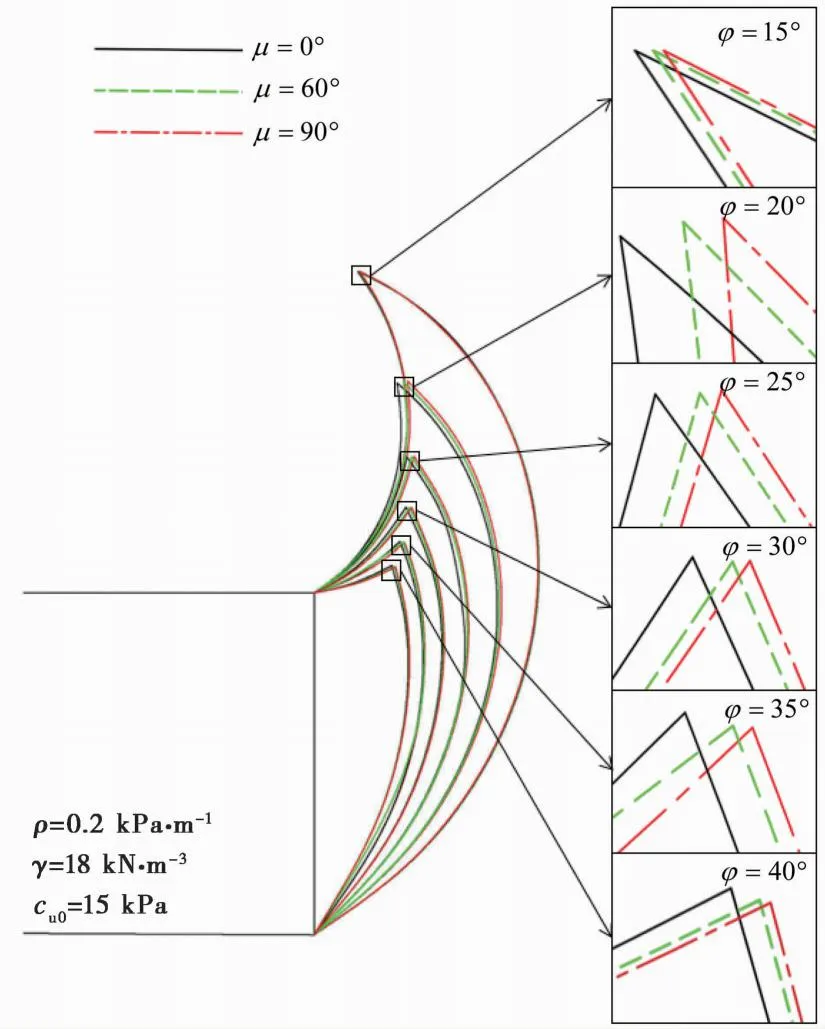
基于上述分析,可以发现非均质系数ρ≠0时,非均质方向角μ的变化会影响开挖面前方断层破碎带黏聚力的分布规律,进而影响开挖面的稳定性。当非均质方向角μ=0°时,断层破碎带黏聚力沿水平方向线性变化,如图9a所示,盾构刀盘顶部a处的黏聚力为ca,刀盘底部b处的黏聚力为cb,且ca=cb,刀盘上破碎岩体的黏聚力均匀分布。当非均质方向角增大到μ=40°时,断层破碎带黏聚力沿AG方向线性变化,黏聚力的非均质方向与x轴夹角为40°,如图9b所示,盾构刀盘顶部A处的黏聚力为cA,刀盘底部B处的黏聚力为cB,若非均质系数ρ>0,则cA 图9 非均质方向角对开挖面前方黏聚力分布规律的影响 3.2.2 内摩擦角与非均质方向角对隧道开挖面极限支护压力的影响 图10反应了开挖面支护压力在不同内摩擦角φ下随非均质方向角μ变化的趋势图。从图10可以看出,当其他参数恒定时,开挖面支护压力随着非均质方向角、内摩擦角的增加而减小,支护压力的减小趋势随着非均质方向角的增大而变缓,表明非均质方向角较大时,非均质方向角的变化对开挖面稳定性的影响较小; 破碎带内摩擦角越大,非均质方向角的变化对支护压力的影响程度趋向减弱,说明内摩擦角增大到一定程度后,非均质方向角的变化对开挖面稳定性的影响有限。 图10 非均质方向角与内摩擦角对支护压力的影响 3.2.3 黏聚力与非均质方向角对隧道开挖面极限支护压力的影响 图11展示了非均质方向角μ和初始黏聚力cu0对开挖面支护压力的影响规律。如图11所示,当其他参数恒定时,隧道开挖面的支护压力随着黏聚力增加而减小,随非均质方向角增大而减小,不同初始黏聚力的支护压力随着非均质方向角变化的趋势相同,不同曲线之间的间距不随非均质方向角变化而发生改变,表明开挖面支护压力的增量比例与黏聚力和非均质方向角的增量比例具有一致的规律性。 图11 非均质方向角与初始黏聚力对支护压力的影响 3.2.4 埋深比与非均质方向角对隧道开挖面极限支护压力的影响 图12给出了隧道开挖面极限支护压力在不同埋深比H/D下随非均质方向角μ的变化曲线。从图12可以看出,当其他参数恒定,埋深比相同时,隧道开挖面支护压力随着非均质方向角增加而减小; 埋深比越大,支护压力随着非均质方向角变化减小的趋势越大,说明埋深比的增加,非均质方向角的变化对隧道开挖面支护压力的影响程度增强。当非均质方向角μ=0°且H/D≥1时,黏聚力非均质分布沿水平方向变化,开挖面前方黏聚力大小不随埋深变化而改变,此时开挖面支护压力不受埋深比变化影响,如图9a所示。 图12 非均质方向角与埋深比对支护压力的影响 3.2.5 非均质方向角与内摩擦角对隧道开挖面破坏模式的影响 图13给出的隧道埋深H=30m,直径D=8.5m。其内摩擦角φ分别为15°、20°、25°、30°、35°、40°,非均质方向角μ分别为0°、60°、90°经过优化后的破坏模式。从图13可以看出,内摩擦角的变化对开挖面的破坏模式的区域大小和形状的都有较大影响。当内摩擦角较小的时候,破坏模式的形状为外形狭长的“牛角形”,随着内摩擦角的增大,破坏范围在横向和纵向上逐渐减小,存在远离开挖面的倾向。在内摩擦角比较小时,破坏范围随内摩擦角的增大明显减小,在内摩擦角增大的过程中,破坏模式的形状和范围受内摩擦角变化的敏感度逐渐降低。这说明内摩擦角较小时开挖面前方破碎带的稳定性较差,产生的失稳破坏区域较大; 内摩擦角较大时开挖面前方破碎带的稳定性较好,形成较为稳定的失稳破坏区。 图13 破坏模式随内摩擦角和非均质方向角变化 图13同时绘制了非均质方向角分别为0°、60°、90°开挖面的破坏模式。从图13可以看出,黏聚力的非均质方向会对破坏模式的形状产生影响,对开挖面破坏区域大小的影响小于内摩擦角的影响。当其他参数恒定,非均质方向角增加时,破坏区域逐渐前倾,向远离隧道面延伸。 整体而言,非均质方向角对破坏模式形状的影响大于对破坏范围的影响,内摩擦角对破坏模式的形状和范围均有较大影响。非均质方向角和内摩擦角的增大均使得开挖面前方的破坏模式由陡变为缓,开挖面前方塌落体由拱顶往下滑的趋势转变为由前方滑落。因此,对于非均质方向角和内摩擦角较大的破碎带,主要加强开挖面前方的加固支护,而对于非均质方向角和内摩擦角较小的破碎带,除了加强对开挖面前方的加固支护,更加要注意对拱顶的加固支护。 对断层野外露头的研究表明,断层破碎带由断面充填物和派生裂缝组成(Tauber et al.,2002; Holland et al.,2006; Mizoguchi et al.,2008)。李少华等(2014)将断层破碎带分为对称的完整断层破碎带结构(断层破碎带包含图14中abmn部分)、不对称的完整断层破碎带结构(断层破碎带仅包含图14中abef部分或femn部分)和不完整的破碎带结构形式(断层破碎带仅包含断面充填物或派生裂缝)。 图14 断层破碎带结构 对于不对称的完整断层破碎带结构和不完整的破碎带结构可以直接应用空间非均质分布函数模型对断层破碎带的黏聚力等相关计算和开挖面稳定性分析。对于对称的完整断层破碎带结构,断层破碎带对称轴两侧的非均质系数不同(ρaf≠ρfn),进行开挖面稳定性分析和黏聚力等相关计算时可以将断层破碎带沿着对称轴(即非均质系数分界线)分成两部分考虑,建立空间非均质分布分段函数模型。 非均质系数分界线的直线方程: x=-tan (π-μ)y+xf (38) 式中:xf为非均质系数分界线与x轴交点的横坐标。 结合式(38)建立空间非均质分布分段函数模型: (39) 如图14所示,断层倾角为90°时,非均质方向角μ=0°,代入式(39)可得: (40) 本文针对断层破碎带的工程特性和黏聚力沿深度线性变化模型的不足,提出了适用于断层破碎带的空间非均质分布函数模型,推导了断层破碎带中盾构隧道开挖面极限支护压力计算公式,重点分析了非均质方向角对开挖面稳定性的影响,主要结论如下: (1)非均质系数角0°<α<90°,即非均质系数ρ>0时,支护压力随非均质方向角增大而减小; 非均质系数角α=90°,即非均质系数ρ=0时,非均质方向角的变化对支护压力无影响; 非均质系数角90°<α<180°,即非均质系数ρ<0时,支护压力随非均质方向角的增大而增加。 (2)非均质方向角μ≠0°且非均质系数ρ>0时,开挖面支护压力随内摩擦角、黏聚力、埋深比、非均质系数的增加而减小。非均质方向角μ=0°且H/D≥1时,开挖面支护压力不受埋深比变化影响。 (3)非均质方向角对破坏模式形状的影响大于对破坏范围的影响,内摩擦角对破坏模式的形状和范围均有较大影响。非均质方向角和内摩擦角的增大使得开挖面前方的破坏模式由陡变为缓,开挖面前方塌落体由拱顶往下滑的趋势转变为由前方滑落。在实际工程中,针对不同非均质方向角和内摩擦角的断层破碎带的加固侧重点应有所不同。 (4)空间非均质分布函数模型体现了断层破碎带的倾斜性和非均质性,考虑了破碎带非均质性沿着任意方向变化,为简单有效地确定断层破碎带中盾构隧道开挖面极限支护压力计算提供了精确可靠的方法。


4 空间非均质分布函数模型在断层破碎带中应用的讨论

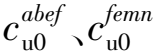
5 结 论
