滑坡堆积体反粒序现象的离散元数值分析*
2024-01-11杨小龙
杨小龙 王 刚
(①山地城镇建设与新技术教育部重点实验室,重庆 400045,中国)(②重庆大学,土木工程学院,重庆 400045,中国)
0 引 言
关于大型滑坡的反粒序堆积现象,最早是由Heim(1932)在对Goldau滑坡进行调查研究时提出的。所谓反粒序堆积现象,它是指滑坡体在移动过程中逐渐形成大粒径颗粒在上、小粒径颗粒在下的反粒序堆积结构的现象。在这种堆积结构中,位于滑坡堆积体上部的硬壳层主要以体积较大的块石、碎石等粗颗粒为主,细颗粒含量较少; 位于中部的主体层,其粒径分布范围极广,以厘米级以下的细颗粒为主,同时夹带少量的粗颗粒; 位于底部的基底层平均粒径最小。在Heim(1932)之后,学者们对国内外众多的大型滑坡进行了现场调查研究,发现了大量存在反粒序堆积现象的地质证据。1986年,Cruden et al.(1986)在对1903年发生于加拿大亚伯达省的Frank滑坡进行详细的现场调查研究后发现,Frank滑坡堆积体中普遍存在反粒序堆积现象,Cruden et al.(1986) 还通过滑坡堆积体的典型剖面对颗粒粒径进行了较为详细的统计分析,对反粒序堆积结构进行了定量分析。Boultbee et al.(2006)借助WipFrag图片分析方法,对2002年发生于加拿大不列颠哥伦比亚省的Zymoetz River滑坡堆积体中的反粒序堆积现象进行了定量描述。王玉峰等(2012)通过对文家沟滑坡、牛圈沟滑坡以及谢家店子滑坡这3个大型滑坡进行现场勘察,对这3个大型滑坡堆积体中的反粒序堆积结构进行了量化,并探讨了反粒序堆积结构的形成机理。此外,学者们还在大量的大型滑坡堆积中发现了反粒序堆积结构(Hewitt,1988; Luzio et al.,2004;Strom,2004; Evans et al.,2006; 郑光等,2019)。
反粒序是大型滑坡的一种典型堆积现象,但是到目前为止,对于大型滑坡堆积体中反粒序堆积现象的形成机理仍颇有争议。总结已有研究成果,反粒序堆积现象的形成原因主要有以下两种观点。
一是颗粒迁移。Bagnold(1954)将快速移动过程中呈离散流状态的滑坡体视为牛顿流体,针对滑坡堆积体的反粒序堆积现象提出了颗粒间离散应力的概念,认为颗粒在移动过程中的碰撞会产生离散应力,该离散应力的大小与颗粒粒径以及剪切应变速率有关,剪切应变速率越大或颗粒粒径越大,颗粒越容易向滑坡体上部移动,从而在滑坡堆积体中形成大粒径颗粒在上、小粒径颗粒在下的反粒序堆积结构。Savage et al.(1988)结合物理模型试验从定量化的角度比较合理的解释了在移动过程中呈密集流状态的滑坡体的颗粒分选过程,提出了“随机振动筛分”机制,该机制是一种重力作用下的、与颗粒粒径大小相关的孔隙填充机制。滑坡体内的小颗粒逐渐向下方随机产生的孔隙内转移,从而形成反粒序堆积结构。Zhang et al.(2011)通过对东河口大型滑坡进行现场调查,研究了滑坡体在滑动过程中颗粒流动的特征以及颗粒尺寸、密度等沿运动路径的变化,认为堆积体中形成反粒序堆积结构的原因是由于力学效应(挤压驱逐机制)和几何效应(随机振动筛分机制)的共同作用。
二是动力破碎。Strom(1994)通过对发生在帕米尔高原以及天山山脉的多处大型滑坡事件进行研究,对各滑坡堆积体中呈现的成层性现象进行了分析,认为滑坡堆积体的反粒序堆积现象是滑坡体在运动过程中的动力破碎造成的。此外,Strom还通过对高加索山脉Ardon河岸的3处高速滑坡堆积体中反粒序堆积结构进行研究,进一步证实了动力破碎对滑坡体在滑动过程中发生反粒序堆积现象的影响。Imre et al.(2010)探究了滑坡体在滑动过程中的动力破碎现象,认为滑坡体在移动过程中基本保持了初始滑坡体的层序关系,但由于滑坡体内不同深度处岩体受到的作用力不同,使得不同深度处岩体的动力破碎程度不同,从而使滑坡堆积体形成反粒序结构。申智好等(2021)基于颗粒离散元数值分析方法,通过调控滑体组成颗粒的级配分布实现对岩块碎屑化效应的表征,为辨识岩块破碎效应对碎屑流滑坡的运移规律及相关灾害防治提供了参考。
在对大型滑坡进行研究的早期,反粒序堆积被认为是贯穿整个滑坡堆积体厚度的现象,但近年来,一些学者在对滑坡堆积体进行更为系统的现场调查和粒径组成分析后,认为反粒序堆积现象仅发生在滑坡堆积体的上表面附近,而位于滑坡体下方的不同粒径的颗粒仍主要呈混合状态(Dunning,2004; Crosta et al.,2007; Dufresne et al.,2016)。本文基于颗粒流程序,探究滑坡体颗粒分形维数、滑坡体积以及加速区长度对滑坡堆积体中各粒径颗粒层序排列的影响规律,以此来探讨大型滑坡堆积体出现反粒序堆积现象的原因。
1 数值模型的建立和验证
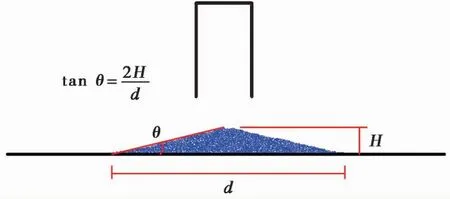
为了探究滑坡体在滑动过程中的颗粒分选过程,林小龙(2019)通过一系列物理模型试验研究了分形维数对反粒序堆积现象的影响,本文根据其试验装置建立的二维数值模型如图1所示。由图1可知,整个数值模型由倾斜滑动面、水平滑动面、初始滑坡体以及挡板构成,可将模型划分为物源区、加速运动区和减速堆积区3部分,坐标原点O设在倾斜滑动面与水平滑动面的交点处。物源区初始滑坡体的宽度为W0,高度为H0,滑动面倾角为θ,加速区长度为L0,滑坡堆积体前缘到坐标原点O的距离为L。
颗粒流程序由颗粒(Ball)与墙体(Wall)这两种最基本的实体构建模型,交替使用运动定律和力-位移定理来分别不断更新颗粒的位置和接触力来模拟散粒体的运动,非常适合模拟滑坡的运动过程(Lin et al.,2015; Feng et al.,2017; Borykov et al.,2019; 陈骎等,2020; 刘伦杰等,2020; 潘清等,2020; 李坤等,2021)。本文采用颗粒流计算程序PFC2D通过模拟图1所示的滑坡模型来探究滑坡体颗粒分形维数(Sammis et al.,1987; Tyler et al.,1992; Crosta et al.,2007)、滑坡体积以及加速区长度对滑坡堆积体中各粒径颗粒层序排列的影响规律。
由于是二维模型,构成滑坡堆积体的各颗粒实际上是具有单位厚度的半径为r的圆盘,因此这里所讲的堆积体的体积实际上是堆积体剖面的面积。数值模拟方案如表1所列,包含了实验尺度的数值模型方案(1~6mm)和现场尺度的数值模拟方案(2~12m),所有数值模拟方案的滑动面倾角均为40°。

表1 数值模拟计算方案
颗粒质量-粒径分布的分形模型由Tyler et al.(1992)提出,具体计算方法为:
(1)
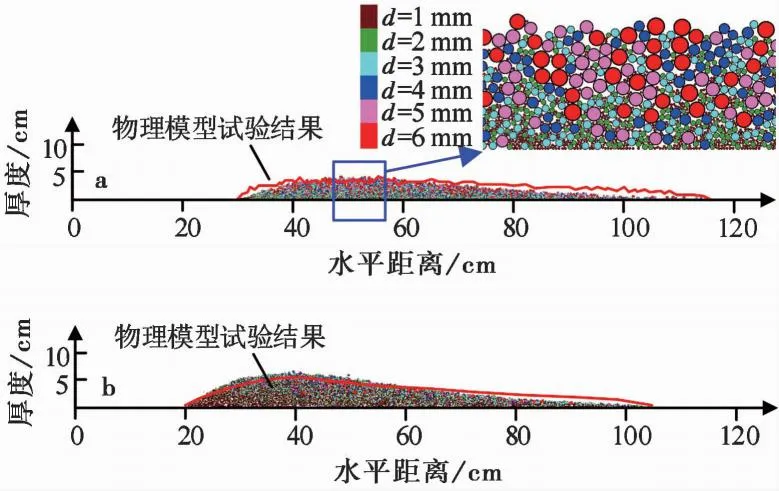
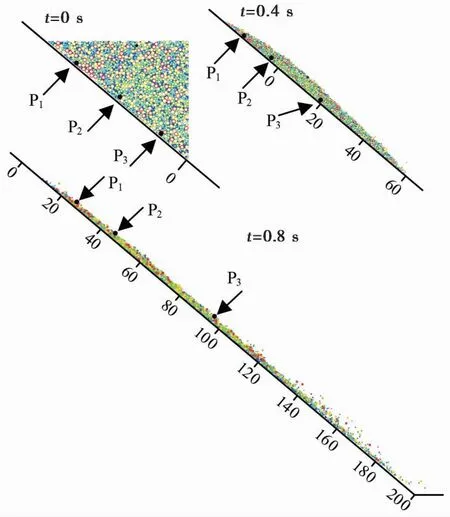
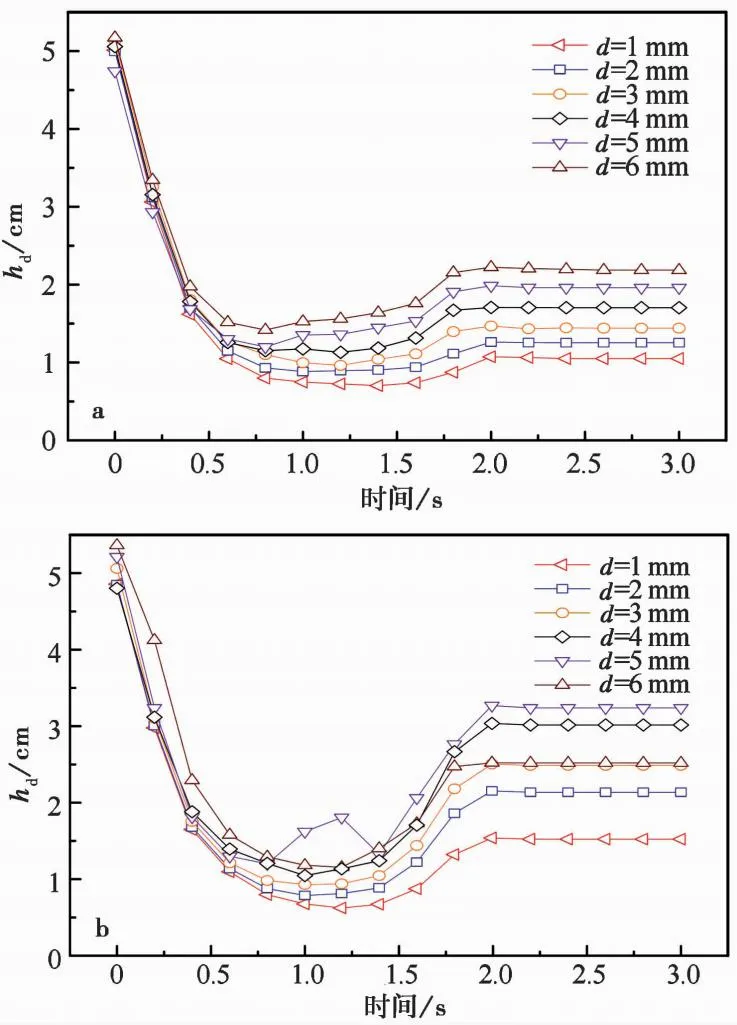
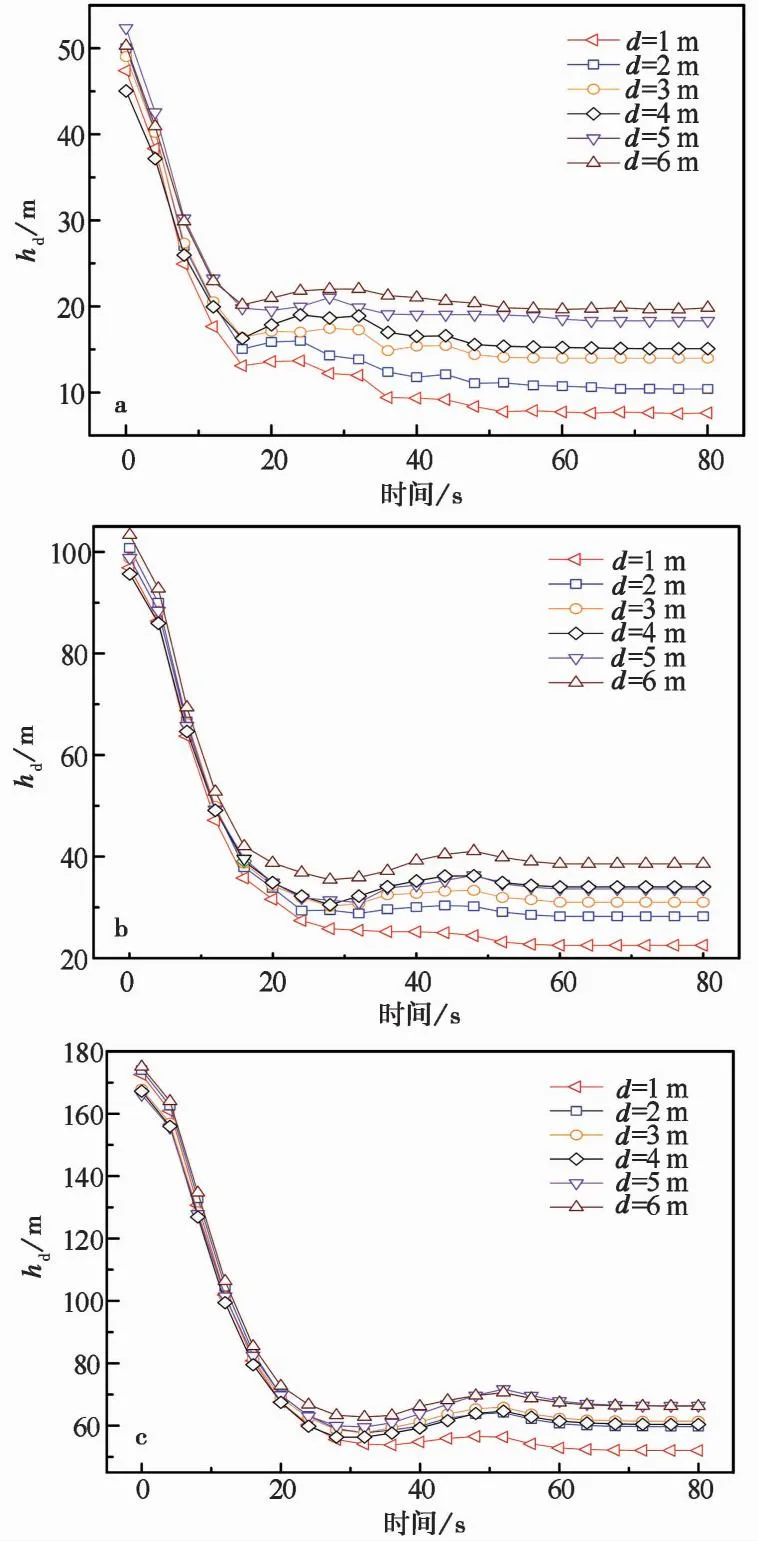
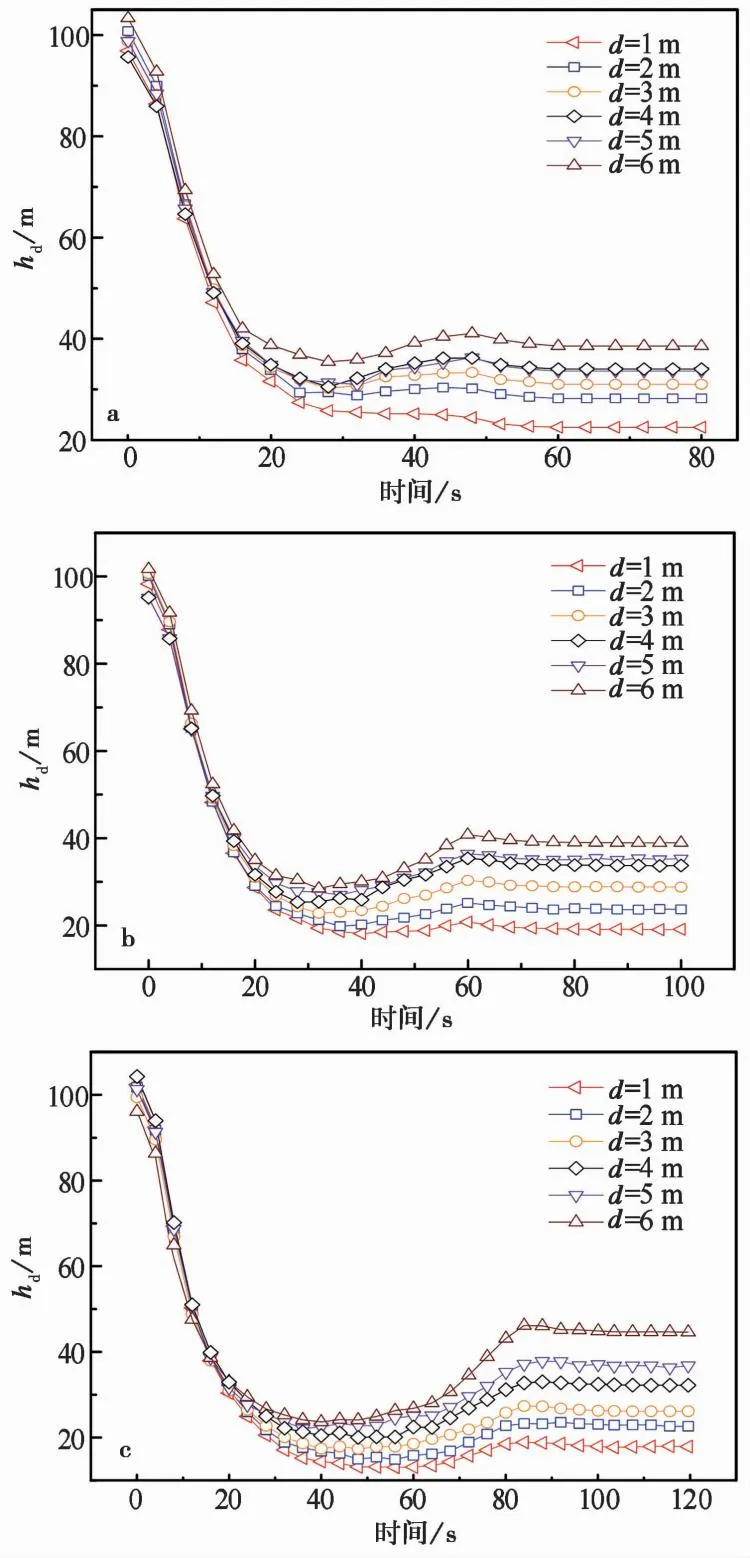
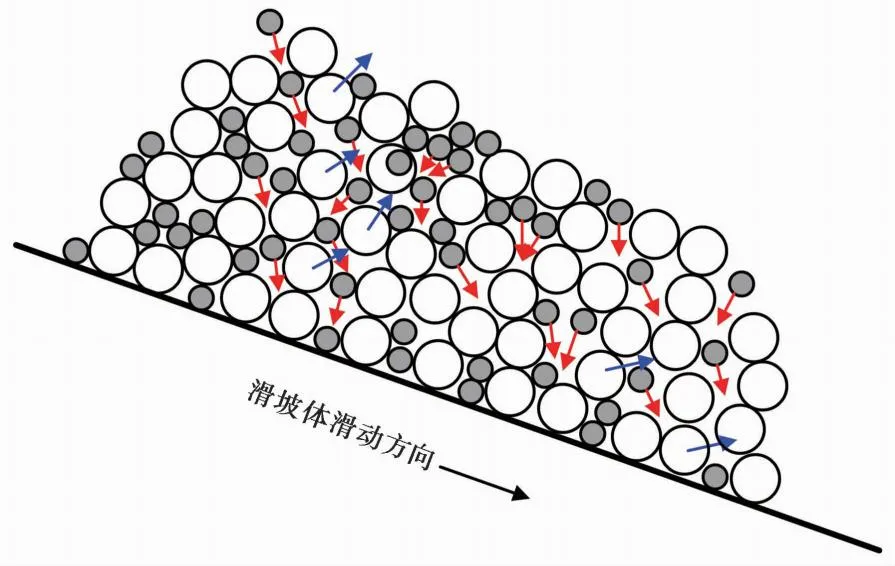
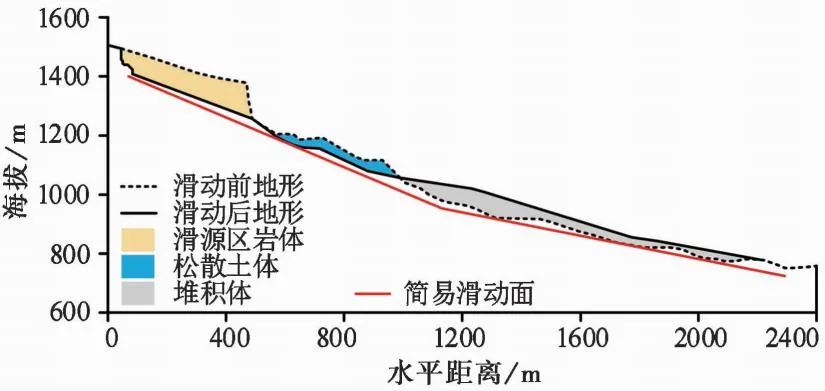
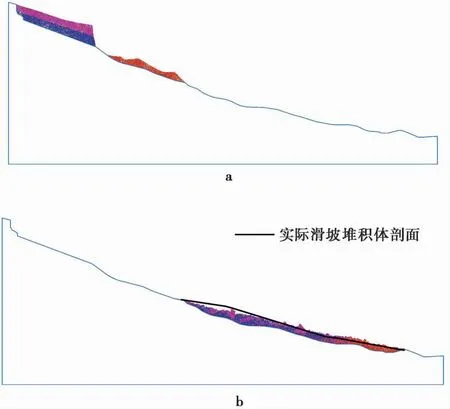
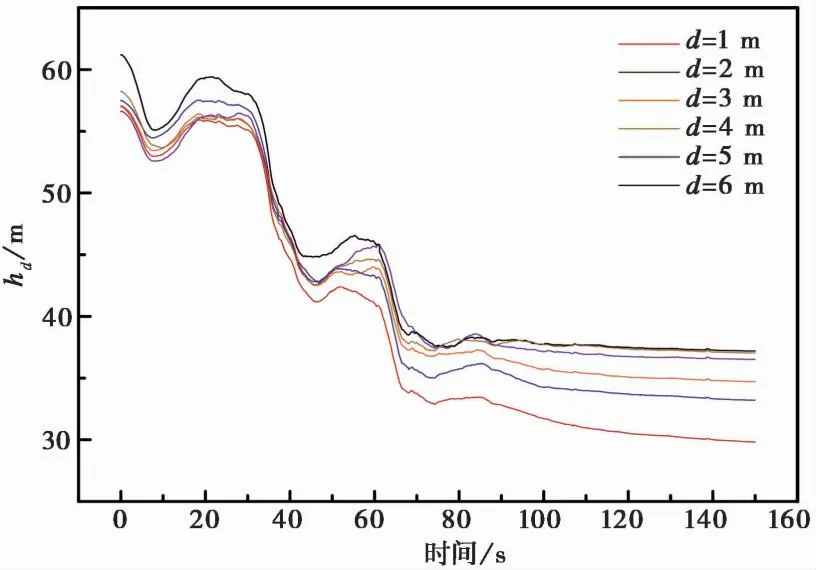
式中:M(r (2) 由上式可知,在双对数坐标下,如果ln(M(r 图2 不同分形维数模拟试样数据 由于物理模型试验(林小龙,2019)中采用的是无黏性颗粒材料,因此,在颗粒流程序中选用线性接触模型来模拟各单元之间的接触行为,并通过摩擦和阻尼来耗散数值模型中的能量,线性接触模型示意图如图1所示。由图可知,线性接触模型由法向和切向的线性弹簧(kn和ks)以及法向和切向的阻尼器(βn和βs)组成。切向接触力与法向接触力间的大小关系遵循库仑摩擦定律,颗粒间的摩擦系数为μc,颗粒与基底的摩擦系数为μw。各参数的大小通过参数标定得到,具体的标定过程为:通过不断调整颗粒摩擦系数、基底摩擦系数以及阻尼等参数,使得数值模型中颗粒堆积体的自然休止角与实际相等,如图3所示。最终得到材料的力学参数如表2所列。 表2 数值模型参数 图3 颗粒流程序参数标定 为了确保颗粒流数值模型的可靠性,首先对林小龙(2019)的物理模型试验进行模拟。林小龙(2019)以高速远程滑坡的分形维数分布特征为依据,通过自行设计的模型试验装置,研究了不同分形维数颗粒流堆积体的反粒序特征,结果表明:随着颗粒流分形维数的增大,细颗粒含量的增加,颗粒流运动过程中不同粒径颗粒的分选作用减弱,导致堆积体中反粒序的发育程度降低。图4为本文借助颗粒流程序得到的数值模拟结果与林小龙(2019)做的物理模型试验结果的对比图。由图可知,对于数值模拟与物理模型试验得到的堆积体,两者在前缘移动距离、堆积体长度以及堆积体最大高度等形体参数上都很接近。因此,可以证明本文的数值模型的计算结果是可靠的。 图4 数值模拟结果与物理模型试验结果对比 图5给出了3个大颗粒在滑坡体运动过程中移动示意图。由图可知,这3个大颗粒一开始位于初始滑坡体的底部,滑坡体开始滑动后,在t=0.4s时这3个大颗粒仍位于滑坡体的下方,但当t=0.8s时,这3个大颗粒已经移动到了滑坡体的表面,揭示了大颗粒在滑坡体滑动过程中向滑坡体上方移动的过程。 图5 颗粒移动示意图 图6给出了颗粒粒径分形维数对滑坡体滑动过程中各粒级颗粒平均高度的影响。各粒级颗粒平均高度通过下式进行计算: (3) 图6 分形维数D对各粒级颗粒平均高度的影响 式中:hd为某一粒级颗粒距滑动面的平均高度,在本文的数值模型中颗粒粒级从小到大分为d1到d6共6个粒级;hi为某一粒级第i个颗粒距滑动面的高度;n为该粒级颗粒的颗粒总个数。 由图6可得到以下结果。(1)D=1.5。当在t=0.2s时,d6粒级的颗粒就已经率先开始分离。当t=0.4s时,d1和d6粒级的颗粒已经分别从滑坡体内部移动到了滑坡体的最下方和最上方。当t=0.6时,d2粒级的颗粒已经完成分离; 同时,d3、d4和d5粒级的颗粒也开始分离。当t=1.0s时,d3、d4和d5粒级的颗粒完成分离,此时,整个滑坡体已经形成反粒序堆积结构。(2)D=3.5。当t<0.8s时,d6粒级的颗粒一直在滑坡体的最上方,而d1~d5粒级的颗粒在0.6s前仍处于混合状态。当t=0.8s时,d1~d3粒级的颗粒完成分离,移动到了滑坡体的下部区域。当t>0.8s时,d5粒级颗粒移动到了滑坡体的最上方,而d6粒级颗粒却开始从滑坡体最上方向滑坡体内部移动,最终与d3粒级颗粒混合在一起,滑坡体没能形成反粒序堆积结构。 图7给出了滑坡体积对滑坡体滑动过程中各粒级颗粒平均高度的影响。由图可知,当滑坡体的颗粒粒径分形维数D=1.5,加速区长度L0=1000m时,随着滑坡体积的增加,滑坡堆积体的反粒序堆积现象越来越不明显。(1)滑坡体积V=44388m3。当t=8.0s时,d1粒级的颗粒就已经率先开始分离,移动到滑坡体的最下方,并且d5和d6粒级颗粒一起移动到了滑坡体的最上方,但d5和d6粒级颗粒之间还未开始分离,d2、d3和d4粒级的颗粒之间也未分离。当t=12s时,d5和d6粒级颗粒之间开始分离,d2、d3和d4粒级的颗粒之间也开始分离。当t=20s时,所有粒级的颗粒完成分离,并且各粒级颗粒按照小粒径颗粒在下大粒径颗粒在上的顺序排列,已经形成反粒序堆积结构。(2)滑坡体积V=177553m3。当t=12s时,d1和d6粒级的颗粒就已经率先完成分离,分别移动到滑坡体的最下方和最上方。当t=32s时,d2粒级的颗粒完成分离,其平均高度只大于d1粒级颗粒。当t=36s时,d3粒级的颗粒完成分离,其平均高度只大于d1和d2粒级颗粒。但是,直到滑坡体完成整个堆积过程,d4和d5粒级的颗粒仍未分离,滑坡体只完成了部分粒级颗粒的分选过程,没能形成整个滑坡体的反粒序堆积结构。(3)滑坡体积V=537024m3。滑坡体中各粒级颗粒的分离程度显著降低,直到t=32s时,d1粒级颗粒才完成分离,移动到了整个滑坡体的最下方。但直到滑坡体完成整个堆积过程,滑坡体中d5和d6粒级颗粒之间以及d2、d3和d4粒级颗粒之间仍未分离,因此在堆积体中未能形成明显的反粒序堆积结构。计算结果表明滑坡体积越大,反粒序现象越不明显,这与Dufresne et al.(2016)通过现场调查得出的结论一致,即反粒序堆积现象仅发生在滑坡堆积体的上表面附近,而位于滑坡体下方的不同粒径的颗粒仍主要呈混合状态。 图7 滑坡体积V对各粒级颗粒平均高度的影响 图8给出了加速区长度L0对滑坡体滑动过程中各粒级颗粒平均高度的影响。由图可知,当滑坡体的颗粒粒径分形维数D=1.5、滑动面倾角θ=40°、滑坡体积V=177553m3时,随着加速区长度L0的增加,滑坡堆积体的反粒序堆积现象越来越明显。(1)加速区长度L0=1000m。当t=12s时,d1和d6粒级的颗粒就已经率先完成分离,分别移动到滑坡体的最下方和最上方。当t=32s时,d2粒级的颗粒完成分离,其平均高度只大于d1粒级颗粒。当t=36s时,d3粒级的颗粒完成分离,其平均高度只大于d1和d2粒级颗粒。但是,直到滑坡体完成整个堆积过程,d4和d5粒级的颗粒仍未分离。因此,滑坡体积V=177553m3的滑坡体只完成了部分粒级颗粒的颗粒分选,仍有d4和d5粒级的颗粒仍未分离,没能形成整个滑坡体的反粒序堆积结构。(2)加速区长度L0=2000m。当在t=8.0s时,d6粒级的颗粒就已经率先完成分离,移动到滑坡体的最上方。当t=56s时,所有粒级的颗粒均完成分离,并且各粒级颗粒按照小粒径颗粒在下大粒径颗粒在上的顺序排列,已经形成典型的反粒序堆积结构。但值得注意的是,d4和d5粒级颗粒的平均高度很接近,表明分离程度并不高。(3)加速区长度L0=4000m。当t=24s时,d1和d6粒级的颗粒就已经率先完成分离,分别移动到滑坡体的最下方和最上方。当t=48s时,所有粒级颗粒完成分离,形成小粒径颗粒在下、大粒径颗粒在上的典型反粒序堆积结构。 图8 加速区长度L对各粒级颗粒平均高度的影响 上述数值模拟结果表明,颗粒粒径分形维数、滑坡体积以及加速区长度对滑坡体在滑动过程中的颗粒分选程度均有较大影响。反粒序的形成主要通过筛分作用和剪切作用来完成,筛分作用使小颗粒向滑坡体下方移动,剪切作用使大颗粒向滑坡体上方移动。 由不同粒径大小颗粒组成的滑坡体在滑动过程中会发生剪切,使滑坡体发生膨胀,颗粒间将不断形成大大小小的孔隙,位于孔隙上方的小颗粒在筛分作用下不断地通过孔隙而向下移动,如图9所示。当滑坡体大颗粒粒径较大且含量较高(即分形维数较小)时,筛分作用更显著,反粒序现象也就越明显。筛分作用还与颗粒受到的上覆压力大小有关,当颗粒受到的上覆压力较大时,颗粒间的孔隙形成过程将会受到一定程度的抑制,从而使得反粒序程度减小。此外,这种筛分作用还与加速区长度有关,加速区长度越大,滑坡体就能得到越充分的“伸展”,从而使滑坡体底部颗粒受到的上覆压力减小,增强颗粒分选程度; 同时加速区长度越大,滑坡体也就有更多的时间来完成反粒序的分选过程。 图9 颗粒分选过程示意图 滑坡体在滑动过程中会发生剪切变形,滑坡体内的各颗粒会因为受到剪切作用而发生滚动,当大颗粒受到的剪力达到某一临界值后,大颗粒可以轻易地通过滚动越过位于其前方的小颗粒,向滑坡体上方移动,最终在滑坡体内形成大颗粒在上、小颗粒在下地反粒序堆积结构(Dasgupta et al.,2011),其示意图如图9所示。这种在剪切作用下的滚动过程也与颗粒受到的上覆压力大小有关,当颗粒受到的上覆压力较大时,该过程将会受到一定程度的抑制,从而使得反粒序程度减小。 2009年6月5日14:51,重庆市武隆县铁矿乡鸡尾山山体,体积约5×106m3的完整性很高的厚层二叠系茅口组灰岩山体经漫长的蠕滑后,由于山体前部“关键块体”被剪断而突然发生大规模崩滑破坏,滑坡体在跃下超过50m高的陡坎后,获得巨大的动能,与基岩发生碰撞并迅速解体,发生高速远程滑坡,滑坡体沿沟谷向下游运动,在沟道里形成平均厚约30m,纵向长度约2200m的堆积区(许强等,2009,2016),最终造成74人死亡。下面结合该滑坡实例进一步对滑坡堆积体的反粒序堆积现象进行分析。 图10给出了鸡尾山滑坡沿其滑动方向的剖面图。由图可知,(1)滑源区滑坡体的海拔最高点位于滑坡体的最左侧,海拔约为1500m,最低点海拔约为1257m; (2)位于滑源区右下方有一小部分松散土体,该部分土体在滑坡发生后将被滑源区滑坡体铲刮而沿滑动面向下移动; (3)滑坡体沿滑动面的水平移动距离约为1716m。 图10 鸡尾山滑坡剖面图(改自Yin et al.(2011)) 由于滑源区滑坡体的主要组成部分为栖霞组灰岩,其物理力学参数如表3所列(Zhang et al.,2019),为了便于计算,数值模型中滑源区滑坡体均采用灰岩。采用单轴压缩试验来对数值模型中滑坡体材料的细观参数进行标定,颗粒间的接触模型采用平行黏接模型。常用参数标定方法为试错法,即多次调整平行黏接模型的各参数大小,直到通过单轴压缩试验得到的试样的应力-应变曲线与实际一致。最终得到的细观参数如表4所列。滑源区滑坡体右下方的松散土体,由于不知道其物理力学参数,所以本文借鉴Zhang et al.(2019)计算时确定的细观参数。对松散土体采用接触黏结模型,颗粒的密度ρ=1500kg·m-3,法向刚度kn=1.0×107N·m-1和切向刚度ks=1.0×107N·m-1,法向黏接强度TF=0.4×106MPa,切向黏接强度SF=0.4×106MPa,摩擦系数μc=0.4。 表3 鸡尾山滑坡岩体力学参数 表4 颗粒流程序细观参数 图11给出了鸡尾山发生滑坡前后的对比图。由图可知,整个滑坡过程可以分为失稳、铲刮、堆积3个阶段,持续时间为150s。在滑坡体滑动过程中,滑源区岩体下方的松散土体被滑源区岩体铲刮并最终堆积在滑坡堆积体的最前方。模拟计算结果与实际结果一致。 图11 鸡尾山滑坡数值模型图 图12给出了各粒径小组的颗粒的平均高度在滑坡体滑动过程中的变化曲线,由图可知得到以下几点认识。(1)在滑坡体初始模型中,由于颗粒为随机生成,所以各粒径小组的颗粒处于混乱状态,此时各粒径小组颗粒的相对简易滑坡面的平均高度hd为:hd1=57.0m,hd2=57.5m,hd3=57.0m,hd4=58.2m,hd5=56.6m,hd6=61.2m。可以看到,d5小组的颗粒位于滑坡最下方; 其次是d1和d3小组,这两个小组的颗粒的平均高度恰好相等; 位于d1和d3小组上方的小组分别为d2、d4和d6小组,这3个小组按从下往上的顺序排列。在初始模型中,各小组颗粒除了d1和d3小组,其余小组颗粒间的平均高度差在0.5m以上,彼此间的分离程序较大。(2)在t=0~18s这段时间,d1小组颗粒的平均高度逐渐减小。当t=18s时,d1小组颗粒的平均高度比其余小组的都小,表明d1小组的颗粒已经在颗粒的分选过程中移动到了滑坡体的最下方,并且在此后的滑动过程中,d1小组的颗粒一直位于滑坡体的最下方。(3)在t=0~50s这段时间,d2~d5 这4个小组颗粒的平均高度差值逐渐减小。这是因为滑坡体在越过陡坎时会发生破碎,使各粒径小组颗粒间的相对位置发生变化,使其处于更加混乱的状态,导致各小组颗粒间的平均高度差值减小。(4)在t=50~58s这段时间,d2和d3两个小组的颗粒在颗粒分选过程中向滑坡体下方滑动,与d1小组颗粒按照小粒径颗粒在下、大粒径颗粒在上的反粒序堆积结构,且在此后的滑动过程中一直维持着反粒序堆积结构。(5)在t=58~88s这段时间,d4、d5和d6这3个小组颗粒继续在动力筛分作用和剪切作用的共同工作用下进行着颗粒分选过程,当t=88s时,d5小组的颗粒完成颗粒分选,与d4和d6小组的颗粒完成分离。但d4和d6小组的颗粒仍没有完成分离,以混合的状态位于滑坡体的最上方。(6)在t=88~150s这段时间,滑坡体逐渐堆积,在t=150s时完成堆积过程,d1、d2、d3和d5这4个小组的层序关系没有发生改变,一直维持着反粒序堆积结构。但是,直到滑坡体完成堆积,d4和d6小组的颗粒仍未完成分离。整个滑坡堆积体没能形成严格意义上的反粒序堆积结构,只形成了部分反粒序堆积结构。 图12 各粒径小组颗粒平均高度变化曲线 本文根据已有的物理模型试验,在颗粒流程序中建立数值模型,研究了滑坡体中颗粒粒径的分形维数、滑坡体积以及加速区长度对滑坡体在滑动过程中的颗粒分选程度的影响,以探究滑坡堆积体出现反粒序堆积现象的原因。可以得出以下初步结论: (1)滑坡体堆积体的反粒序堆积现象是动力破碎以及颗粒分选的结果,颗粒分选是在动力筛分作用和剪切作用的共同作用下完成的。滑坡体在滑动过程中因发生颗粒破碎而形成不同粒径大小的颗粒,动力筛分作用使小粒径颗粒通过大粒径颗粒间的孔隙向滑坡体下方移动,剪切作用使大颗粒越过小颗粒向上移动,最终使不同粒径的颗粒完成颗粒分选过程,形成反粒序堆积结构。 (2)颗粒粒径分形维数、滑坡体积以及加速区长度均对滑坡体内的颗粒分选程度有较大影响,颗粒分选程度随分形维数的减小而增强,随滑坡体积的增大而减弱,随加速区长度的增加而增强。 (3)数值模拟再现了鸡尾山滑坡堆积体中存在的反粒序堆积现象。滑源区岩体由于碰撞以及受到的拉力超过其抗拉强度等原因而发生破碎,形成粒径大小不一的颗粒,并在滑动过程中完成颗粒分选,形成大粒径颗粒在上、小粒径颗粒在下的反粒序堆积结构。

2 结果分析
2.1 分形维数的影响
2.2 滑坡体积的影响
2.3 加速区长度的影响
3 反粒序形成机制分析
4 鸡尾山滑坡模拟


5 结 论
