考虑渗滤效应的全风化花岗岩体脉动注浆扩散规律*

窦金熙 张贵金 蒋煌斌 匡楚丰 张 熙

(①长沙理工大学水利工程学院,长沙 410114,中国)(②水沙科学与水灾害防治湖南省重点实验室,长沙 410114,中国)(③国家电投集团五凌电力有限公司,长沙 410114,中国)

0 引 言

全风化花岗岩(土)体工程力学性状特殊( 李术才等,2013; 张聪等,2019a,2019b),作为建筑地基时,往往存在地基承载力不高,地基变形较大的问题; 作为防渗体时,多存在透水性好,防渗处理难度大,防渗标准难以满足工程要求的问题。脉动注浆工艺,是一种深厚覆盖多孔介质地层型地基处理的有效方法(张聪等,2019a),可有效解决稳压注浆孔底难以升压、浆液扩散不可控、防渗加固效果差等关键技术问题。虽然脉动注浆工艺,已经得到一定应用,但是,仍存在脉动压力控制作用下浆液扩散规律、渗滤效应不明等亟待研究的问题。

注浆浆液可分为溶液型和悬浮液型,无论是宾汉流体和幂律流体型皆属于悬浮浆液。悬浮颗粒浆液在多孔介质中最大穿透距离主要由两种不同的流动停止机制控制:流变阻滞机制和渗滤机制(Yoon et al.,2014)。对于流变阻滞机制,浆体的停止主要受压力梯度控制; 对于渗滤机制,颗粒浆液渗透的停止取决于浆液和土体的相对物理配置,即取决于浆液的颗粒粒径和土体孔隙大小等; 介质中随着浆液流动,颗粒发生渗滤,被渗滤的颗粒堵塞了流动路径,则可导致浆液流动停止(Herzig et al.,1970; Axelsson et al.,2009)。注浆过程中发生渗滤效应是多孔介质孔隙被充填普遍存在的现象和产生颗粒淤积的主要原因(Gustafson et al.,1996),因此颗粒的扩散受渗滤机理影响较大,在渗透注浆中起着非常重要的作用。脉动注浆周期压力下,悬浮颗粒浆液扩散的渗滤机理研究滞后于工程实践。

目前,针对脉动注浆,研究仍处于浆液扩散初步阶段,如张聪等(2018a,2018b)对幂律流体和宾汉流体的脉动注浆渗透扩散机制做了研究; 张贵金等(2016),对松软地层脉动注浆的止浆机制做了研究。且国内外学者就渗滤效应的研究成果都基于稳压注浆; 如李术才等(2015,2017)对砂土介质中考虑渗滤效应的注浆扩散规律,及渗滤效应下多孔介质渗透注浆的扩散规律做了研究,得出了砂土介质颗粒浆液的渗滤系数。冯啸等(2016)对深层渗滤效应下水泥浆动界面特征做了研究。朱光轩等(2017)对渗滤效应下沙层劈裂注浆的扩散规律做了算法研究。Bouchelaghem (2009)和Sangroya et al.(2017)对水泥悬浮浆液渗滤过程中细砂渗透演化进行了多尺度模拟,建立了膨润土浆液在颗粒土中恒通量渗透的渗滤模型;Yoon et al.(2015)做了基于渗滤模型的膨润土颗粒可灌性研究,并提出了一种用于评价膨润土浆液通过颗粒土的最大渗透距离的渗滤模型。虽然学者对灌浆渗滤效应研究取得了一定成果,但都基于稳压条件,且脉动压力作用条件下注浆扩散机制及其渗滤机理尚不明确。

鉴于此,本文基于脉动注浆压力周期变化特征,推导脉动注浆浆液扩散运移方程; 依托COMSOL 多物理场耦合平台,结合MATLAB开发考虑渗滤效应的脉动注浆扩散数值模拟程序; 设计一套脉动和稳压注浆模拟试验装置,研究脉动注浆与稳压注浆的浆液扩散差异; 并采用数值模拟构造随机孔隙率非均质模型,通过以上方法的相互验证,来揭示脉动注浆压力控制下全风化花岗岩(土)体中的扩散规律,以期为脉动注浆技术工艺的工程应用,提供科学的理论指导。

1 脉动注浆理论模型

脉动注浆的实现原理如图1所示,从图1中可以看出,脉动注浆不同于稳压注浆,稳压注浆过程中,无论是入口压力还是出口压力都是恒定的,但是脉动注浆的压力存在脉冲段和间歇段两部分。脉冲段的压力为脉冲泵正常注浆时间段,间歇段的压力为0,即压力泵停止泵送压力。

1.1 脉动注浆扩散解析方程

对于颗粒型的悬浮浆液,如高浓度的水泥和黏土浆液,通常具有屈服应力,在屈服应力以下,浆液表现出具有无限黏度的类似固体的行为。当施加的应力超过屈服应力时,浆液表现为液体状态,黏度随施加的剪切速率而变化。黏土浆液的这种流变行为可以用宾汉姆流体模型描述:

τ=τy+k′γn′

(1)

式中:τy为屈服应力(Pa);γ为剪切应变率(%);k′为流动特性指标;n′ 为流动行为指标。流动行为指标控制着流动的黏性阻力,假塑性流体(n′<1),膨胀流体(n′>1),宾汉流体(n′=1)。

根据学者已有研究表明(Gustafson et al.,1996),无论是基于压迫滤水论和流动沉积论,浆液穿透多孔介质的孔隙皆由颗粒粒径决定,粒径越小、多孔介质孔隙越大、穿透距离越大。同时,考虑浆液的屈服应力、土体参数和注入压力联系起来,以估计黏土和水泥悬浮液通过颗粒土的最大渗透距离,Greenwood (1991)提出了如下等式:

(2)

式中:S是穿透距离(cm); Δp(=P-u)为脉动压力P与孔隙水压力u之差(Pa);τy为屈服应力(Pa);α为最小粒径(mm)。

对于土体的参数,考虑孔隙率、土体密度和级配以及颗粒形状的变化,Jefferis (2003)提出了考虑这些因素的方程:

(3)

式中:n为土体孔隙率(%);f为考虑土体内部流道几何形状和弯曲度的因素(一般为0.3);D10为土体的有效粒径(mm)。

浆液流经脉冲泵时,在阀前后会产生压降Δp,一般采用单通道压降计算公式进行简化计算,压力和流量的关系表达式为:

(4)

式中:A为钻杆的流量面积(m2);Q为浆液的流量(m3·s-1);Cd为活塞阀的流量系数,在实际超过雷诺数时,一般取常数0.6～0.8;ρ为浆液密度(kg·m-3);Δp为浆液流经活塞阀产生的压降与孔隙水压力u之差(Pa)。

考虑土的比表面积的宾汉姆流体,在脉动压力下最大穿透距离的理论方程:

(5)

式中:ω为土体的比表面积(m2·m-3);U为土体不均匀系数(D60/D10)。

脉动压力下宾汉姆流体的扩散解析方程适用条件:①在假设浆液的扩散过程中为层流的基础上推导出,不适用于旋喷的紊流扩散。②对于纯水泥浆液(水灰比0.5～0.7)和黏土掺量在30%以上的水泥浆液型幂律流体不适用。

1.2 脉动注浆扩散渗滤模型

浆液扩散渗滤效应主要产生于脉动持续段,所以利用平流-离散方程来表述悬浮颗粒在多孔介质中的流动,通过对包括固相和液相在内的特征体积的空间平均,推导出控制方程。控制方程表示为:

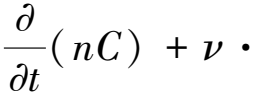
(6)

式中:n为孔隙率(%);C为溶质浓度(L2·T-1);V为实际流体速度(m·s-1);D为水动力弥散张量(L2·T-1维数);σ为初始单位孔隙体积沉积的浆液颗粒质量(M·L-3)。

假设颗粒间应力对颗粒沉积的抑制作用最小,忽略孔隙率的变化、浆液浓度变化、弥散度变化而得出的。则渗滤速率的动力模型表示为:

(7)

式中:λ为沉积系数(1/T)。为了实现式(6),做了以下假设:1)水动力弥散对水泥浆的稀释作用被忽略,渗流是颗粒浆液流动的主导作用(Raupach et al.,1982); 2)孔隙度变化不大(∂n/∂t≈0)。式(6)变为:

(8)

式中:V为实际流速(cm·s-1);V=v/n(v为平均流速(m·s-1);n为孔隙率(%)。

浆液需要一定时间来流经多孔介质,因此,浆液到达多孔介质中某一位置的时间沿其长度是不相同的。因此,在相同的相对时间尺度下,应比较土体中浆液的性质。保留时间函数表示为:

(9)

式中:ξ(x,t)为保留时间函数;x为元素在多孔介质中的位置;V为实际流速(cm·s-1);t为时间(s);x/V为浆液在多孔介质中达到x位置所需的时间。

通过引入保留时间的概念,将偏微分方程(式(9))简化为常微分方程。Reddi et al.(1997)提供的解决方案为:

(10)

式中:f1为边界条件的函数;f2为初始条件的函数;U为heaviside单位阶跃函数。使用以下初始条件和边界条件求解式(10):

C(x,0)=0=f2(x)=0,f1(t)=c(0,t)=C0

(11)

浆液的浓度由以下公式获得:

(12)

单位孔隙体积在孔隙空间中沉积的浆液颗粒量用表示:

(13)

对式(13)积分,得到初始单位孔隙体积在基质中保留的浆液颗粒量为:

(14)

根据Kim Y S et al.(2009)研究,提出的三维球面计算的逐级方法。克服了式(14)悬浮浆液孔隙率和恒定的颗粒沉积速率随时间变化的局限性。

砂柱被划分为高度无穷小的体块(每个体块在柱的横截面上延伸)Δh(=hi-hi-1)。影响浆液渗透的因素(如孔隙内流体速度、孔隙度和过滤系数)被认为在每个无穷小体积块内是恒定的。每个块上的注入时间由下式表达:

(15)

式中:下标i和j分别为空间节点和时间步长(i≤j); Δh为hj-1和hi之间的距离(5mm);nij为hj-1和hi时间增量j的孔隙率;kij为hj-1和hi时间增量j的透水率; (γg)ij为hj-1和hi浆液时间增量j的单位重量; (μg)ij为hj-1和hi时间增量j的浆液黏度;i′为水力坡降假设在注射过程中是恒定的。

由于渗滤过程的动态性(Bai et al.,1997),沉积系数(k)难以确定(Saada et al.,2005),因此要根据实验结果反分析得到(Bouchelaghem et al.,2001)。

Reddi et al.(1997)提出了一种基于粒子捕获概率方法的过滤速率的封闭表达式。提出集总参数θ概念,集总参数反应离子强度、pH值和流速的影响,θ值越大表明渗滤位越高。θ值用指数函数表示:

(16)

式中:θ为集总参数; 其中θ0为常数,视离子条件而定;vcr为无颗粒沉积时的临界流速(cm·s-1)。土体的vcr接近0.1cm·s-1(Santagata et al.,2003)。

将粒径分布曲线细分为平均粒径半径、Ri、权重分数、wi的粒径范围。在每个尺寸范围内,孔隙体积用已知宏观孔隙比下的等效单孔半径来表示,即孔隙半径(r)与颗粒半径(R)之间的关系。

(17)

式中:Ri为粒子半径(mm);ri为等效孔隙半径(mm);α*为表示流动方向有效孔隙长度的参数(假设为圆柱形),α*在淤泥和粗砂之间分别为3～15mm(粒子半径从10-3～1mm),α*砂值为9.11mm(Kim J S et al.,2009)。沉积系数取决于孔隙流体的速度,其表达式为:

(18)

式中:Vij为hj-1和hi时间增量j的孔隙速度;a为迁移颗粒半径;m和b分别为对数正态孔隙半径分布的均值和标准差;θ为集总参数。

在每个无限小体积块的中心可以计算出粒子的沉积:

(19)

然后计算为沉积量随时间的总和,利用密度关系,得到了块体处多孔介质的新孔隙率:

(20)

式中:nij为hj-1和hi时间增量j的新孔隙率;n0为多孔介质的初始孔隙率;σij为hj-1和hi时间增量j的每单位体积的多孔介质中渗滤粒子的质量;Gs为固体颗粒的比重;γw为水的单位重量。当孔隙率接近零(e≈0)时,浆液流动停止。

当孔隙率接近零(n≈0)时,浆液流动停止。基于Kozeny-Carman方程和水力半径模型(Reddi et al.,2000),内在透水率的变化公式如下:

(21)

由于前一个区块的颗粒损失,随着渗滤的进行,浆液浓度降低,影响了后一个区块的单位重量和浆液流动的表观黏度。计算了颗粒浓度、单位质量和表观黏度的变化:

Ci+1j=Cij-Δσij

(22)

(23)

(24)

式中:μw、μeq,0分别为水的黏度和浆液的初始黏度(mPa·s);γg为浆液的单位重量;φ0为浆液中初始的颗粒体积分数;φ为浆液中当前的颗粒体积分数。

由于注浆过程是连续的,应考虑体积块体之间的耦合。在计算每个块体的最大运行时间时,考虑耦合从而控制了任意给定时间步长j的注浆过程:

Δtj=max(Δt1j,Δt2j,Δt2j…Δtij)

(25)

在确定的时间内,利用式(20)～式(24)计算单元中部的渗滤量、固有渗透率的变化和相应的体积响应。然后计算注浆前沿的位置为:

h=(j-1)·Δh

(26)

1.3 脉动注浆“浆-土”耦合方程

1.3.1 脉动压力控制方程

采用三角形波函数,对脉动压力的浆液控制方程进行建模。方程如式:

(27)

式中:T为一个周期;A为脉冲最大压力;t为时间。

1.3.2 理查兹方程

浆液在多孔介质的扩散采用非饱和流理查兹方程,同时结合MATLAB二次开发得到考虑渗滤效应的脉动注浆平流-离散方程内嵌得到COMSOL Multiphysics平台的溶质运移模块进行耦合,来表述悬浮颗粒在多孔介质中的流动,理查兹方程如下所示:

(28)

式中:P为压力;ρ为流体的密度;为Hamilton算子;u为流体的流速;Qm为流体的质量源项;κ为渗透系数。

1.3.3 固体力学方程

多孔介质固体的应力和应变,根据固体力学理论,方程如下式:

0=·s+Fv

(29)

s=sad+C︰εel,εel=ε-εinel

(30)

εinel=ε0+εext+εth+εhs+εpl+εcr+εvp

(31)

sad=s0+sext+sq

(32)

(33)

C=C(Ε,ν)

(34)

式中:E为杨氏模量;ν为泊松比;为Hamilton算子;εinel为弹性应变量;u为流体速度;Sad为弹性体应变周长;ε0、εext、εth、εhs、εpl、εcr、εvp为应变分量;Fv为体积力。

1.4 算法计算流程

采用数值模拟多物理场耦合软件COMSOL MultiPhysics溶质运移模块,并结合MATLAB二次开发自定义PDE方程,通过预定义地层孔隙率随机分布函数和脉动压力周期函数(雷晓丹等,2020; 征西遥等,2020),考虑浆液黏度时变性与地层的非均值性(朱遥等,2020)。具体计算步骤如图2所示:

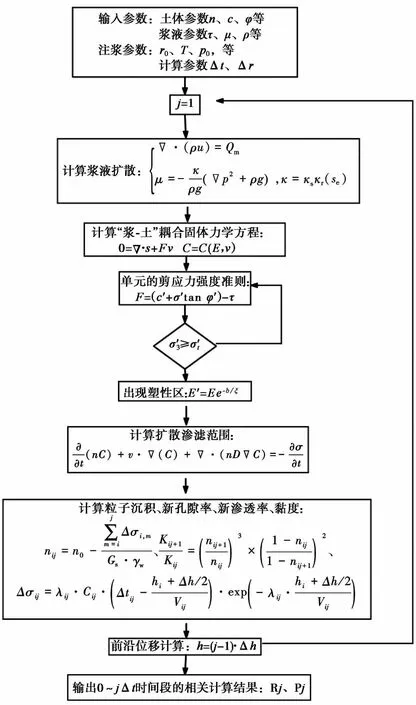
图2 注浆扩散过程算法流程图

2 脉动注浆扩散数值模拟

2.1 模型建立与参数设置

根据注浆模型试验设备,同时考虑数值模拟可以更方便数值试验,覆土深度增加为1m,左右扩散距离均设为1m,二维模型为2×2m的方形,注浆孔内径为模拟真实注浆管规格0.056m。注浆时间为20min,浆液流变特性如表1,网剖分和地质模型格如图3所示。脉动注浆数值模拟扩散做了如下假设:①浆液符合假设的宾汉姆流体模型,除了流变特性不发生其他变化。②注浆过程中无论是持续段和间隔段,脉动输出压力不考虑管路损失。全风化花岗岩体和浆液数值模拟参数由室内实验和原位实验得出,如表2所示。

表1 浆液流变方程

表2 数值计算基本参数

图3 网格剖分与初始随机孔隙率多孔介质模型

2.2 数值模拟结果分析

采用浆液在土体内饱和度对土体的加固防渗效果进行判定。认为浆液在土体内无论发生了劈裂、挤密、渗透等的扩散形式,都将会反映在土体的孔隙率和浆液的浓度变化,所以浆液在土体内的饱和度可以作为土体防渗加固的判定依据。

图4a～图4d为多孔介质脉动注浆浆液扩散饱和度随时间变化图,从图中数值模拟结果可以得出,脉动注浆压力控制下,地层模型中注浆孔处出现了>90%的饱和度加固圈,浆液扩散呈椭圆形与真实注浆浆泡类似; 且从图中还可以看出,浆液饱和度随着时间的推移,5～20min时段饱和度圈不断扩大,离注浆孔距离越近的位置饱和度越高; 饱和度>50%的加固圈由于渗滤效应的存在,浆液扩散范围更大,呈均匀分布扩散,没有出现劈裂的浆脉。说明在脉动压力控制下,渗滤效应让小颗粒穿过大孔隙运移到了更远的距离,大颗粒聚集于出浆口出现了挤密注浆; 同时也间接表明多孔介质孔隙率得到有效降低。

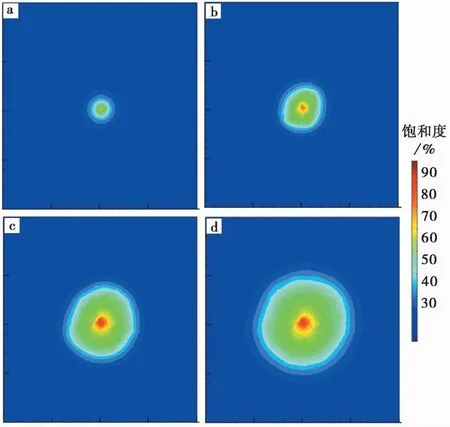
图4 脉动注浆浆液扩散饱和度随时间变化云图

图5a～图5d为多孔介质稳压注浆浆液扩散饱和度随时间变化图,从图中数值模拟结果可以得出,稳压注浆,浆液在地层中出现了明显的浆脉,5min时浆液扩散范围小,随注浆时间的延长10min时,注浆口附近浆液饱和度超过90%,开始出现浆脉,但是浆脉厚度小。当注浆时间延长至15min时,出现了明显的4条浆脉,20min时浆脉的厚度不断增大,部分浆脉开始出现分支。且渗滤范围小,饱和度>50%的扩散圈只存在于浆脉边缘。根据以上现象,表明在稳压控制下,浆液扩散不易控制,重复劈裂明显; 且浆液的渗滤扩散受阻滞,前期浆液扩散对多孔介质充孔隙率填充阻碍了后续颗粒进入,持续注浆已无效果。

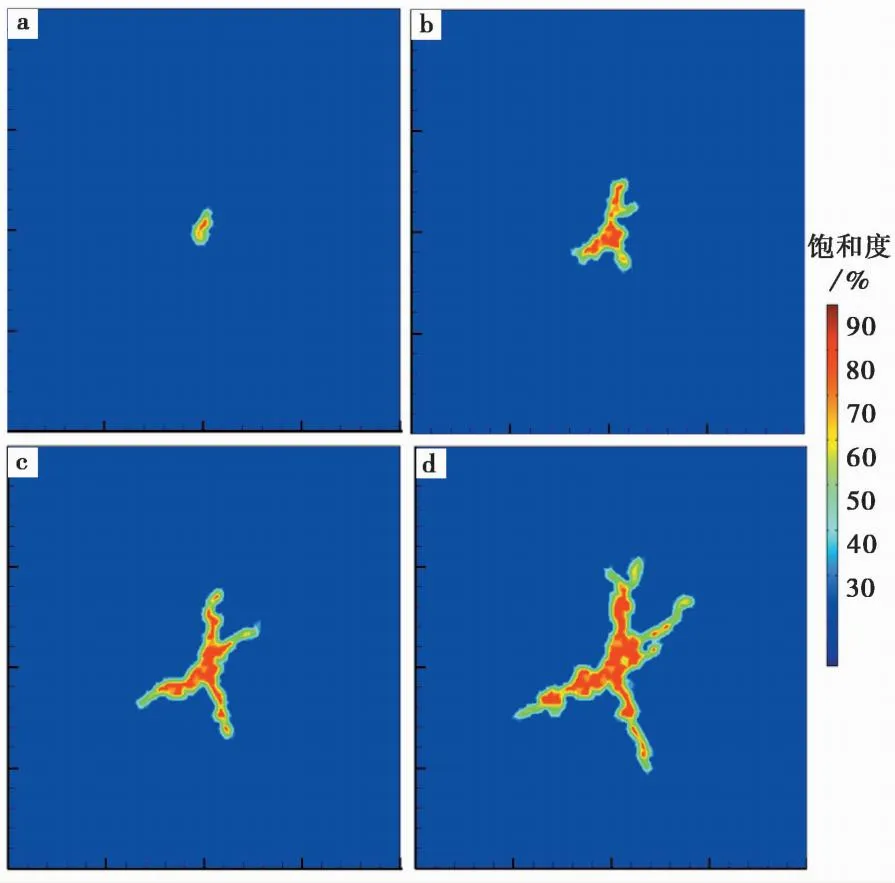
图5 稳压注浆浆液扩散饱和度随时间变化云图

图6为注浆管的出浆口处浆液应力变化,从图中可以看出在脉动周期压力控制下,出浆口处浆液的压力应力呈波浪变化,且随着时间的推移应力变小,说明随着时间的推移浆液内部应力,随着扩散距离的增加,应力逐渐变小,但是内部脉动应力没有改变。图7为模型左边界的应力随时间的变化,从图中可以看出模型边界的中间处应力最大。说明该受脉动周期压力的控制下,浆液的应力集中于出浆口,这有利于地层的抬动控制,减小劈裂注浆带来的无效扩散。

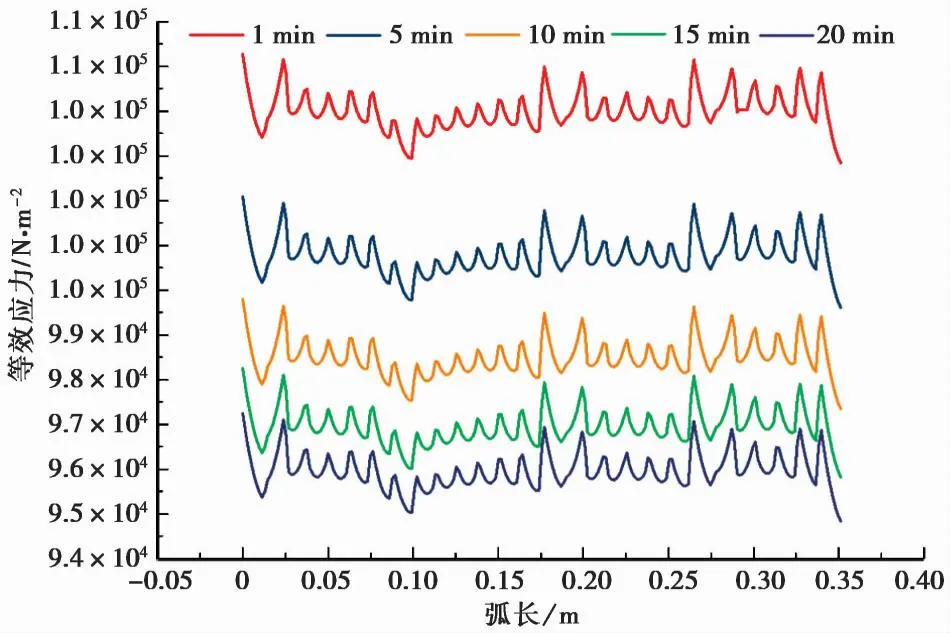
图6 模型出浆口应力随时间变化图

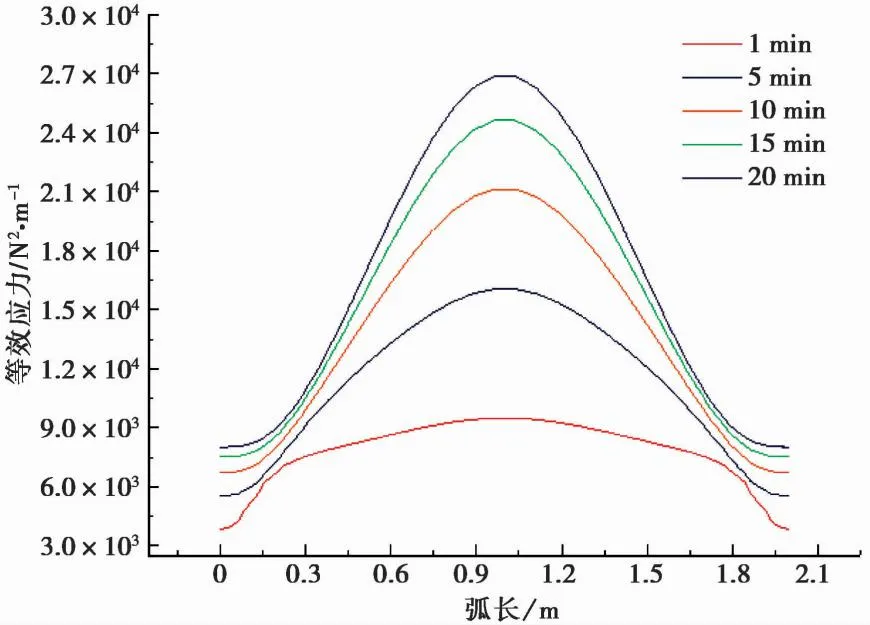
图7 模型边界应力随时间变化图

综上可知,脉动压力下宾汉流体悬浮液颗粒扩散、充填多孔介质孔隙相比稳压更充分,扩散更均匀; 同时,间接表明考虑渗滤效应的脉动注浆扩散,能有效反映浆液的扩散影响范围和分布区域。

3 脉动注浆扩散模拟试验

为了有效得出脉动注浆与稳压注浆扩散渗滤效应机理的差异,悬浮浆液的扩散机制,试验设计采用屏浆方式。根据水工建筑物水泥灌浆施工技术规范(DL/T5148-2012),拟通过封闭外部环境迫使浆液沿多孔介质路径扩散。

3.1 试验装置

采用团队自设计的试验装置开展体脉动注浆和稳压注浆渗滤扩散模拟试验。其中脉动试验装置采用YLSD-2型手摇注浆机,注浆流量为6～10L·min-1,最大工作压力4MPa。稳压灌浆装置采用DMAR-04型电动灌浆泵,灌浆量450L·h-1,灌浆压力:1.5～3MPa。受灌体容器:受灌体容器为高650mm,直径为450mm圆柱形钢罐。为了模拟稳压与脉动注浆渗滤效应机理,注浆时受注灌上部机械封闭,形成屏浆环境,具体试验装置如图8所示。

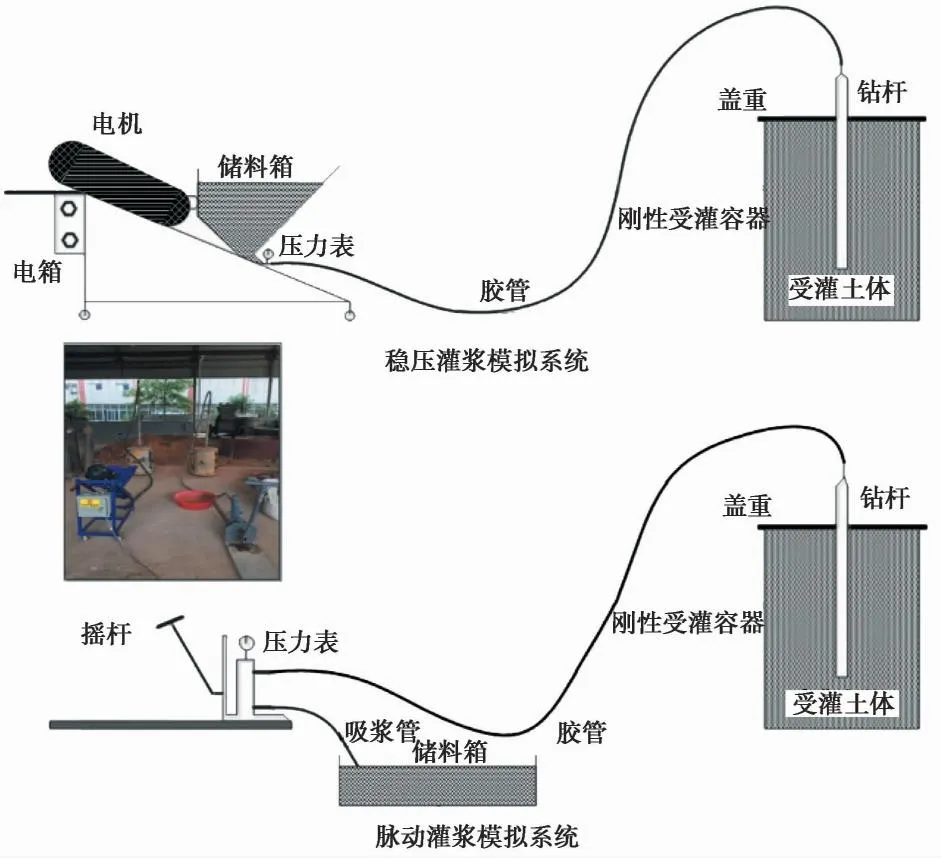
图8 脉动与稳压注浆试验装置

3.2 试验方案

3.2.1 试验材料

采用全风化花岗岩(土)体构造地层,试验地层的参数构造依据,来自云南红河州邦干水库坝肩,并根据现场试验获得。风化岩土体密度1650 kg·m-3。按照《岩土工程勘察规范》确定是属于中砂。

3.2.2 注浆材料

根据课题组之前研究(Zhang et al.,2017; Liu et al.,2019; Li et al.,2020),采用黏土-水泥作为注浆浆液。不同水固比的浆液性能参数见表3。本次试验采用的浆液配比为典型的宾汉姆流体浆液,水固比为0.8,其浆液的黏度时变模型符合表1中的公式(2)。

表3 不同水固比浆液性能参数

3.2.3 控制参数

试验通过控制压力不控制流量为原则,以注入时间为停注标准,对受注体上部加盖封死形成屏浆环境,有利于浆液渗滤效应的产生。稳压注浆和脉动注浆入口压力均设计为压力0.2MPa; 单次试验时间为20min,脉动持续时间为2s,脉动间歇时间为4s,依次类推其他脉动持续和间歇时间。

3.3 试验结果分析

注浆完成后,待浆液凝固7d后打开受灌体,并清理未胶结的土体。稳压注浆的浆液扩散形态如图9所示。从图9中可以看出浆液形成了一条或者两条主浆脉,并伴随着次浆脉,存在劈裂的与渗透、挤密并存的复合注浆。由于稳压注浆,浆液会在恒压的驱使下沿着单一薄弱裂隙面或小主应力面不断劈裂扩散,导致稳压注浆对于多孔介质浆液的扩散极不可控。也间接表明,稳压注浆对于地层的防渗加固存在明显的不可控现象,同时还存在浆液扩散距离扩大,导致了很多无效灌注的情况。

图9 稳压注浆试验浆液扩散形态

图10为脉动注浆参数下浆液扩散形态土。从图10中可以看出浆液形成了椭球状胶结体,浆液没有呈脉状扩散,与稳压注浆的扩散图差异较大。说明脉动注浆参数控制下,浆液的扩散在土体内没有沿着单一裂隙面持续灌入,扩散呈整体辐射较均匀。原因分析表明,频率输送压力导致浆液施加给土体颗粒的荷载不能形成骨架力链(窦金熙等,2021),荷载被均匀分布在砂质土的颗粒上,不容易形成劈裂浆脉的发生条件,从而浆液不会持续一直扩散,先进入的浆液会阻滞后进入的浆液,浆液的扩散在内部之间存在制约,从而能够形成浆泡。

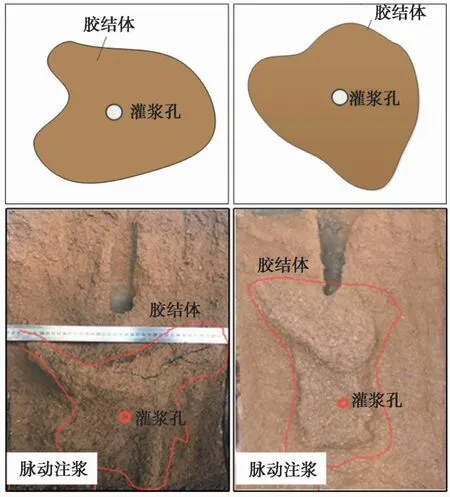
图10 脉动注浆试验浆液扩散形态

4 讨 论

根据解析方程理论计算,采用数值模拟和室内试验脉动注浆的扩散距离进行了验证,在砂质土中,注浆压力取0.2MPa时理论计算的距离为17.8cm,室内试验平均为16.4cm,数值模拟显示扩散距离为18.2cm,扩散范围区间的误差在8%之内,具体扩散距离如图11所示。

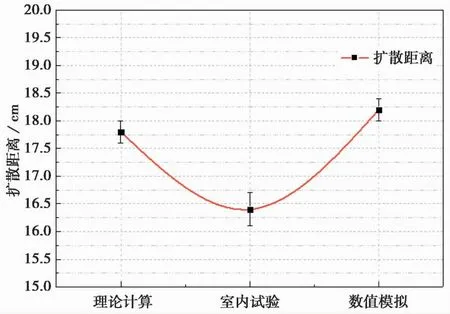
图11 理论计算、室内试验、数值模拟浆液扩散距离对比图

从图11中可以看出,理论计算与数值模拟得出的渗滤扩散距离相近,但是室内试验相比理论计算、数值模拟存在一定误差。脉动注浆的数值模拟扩散均匀度较高呈圆形和室内试验存在偏差,分析认为:1)理论计算、数值模拟属于理想计算,而室内试验,浆液注浆压力均为手动脉动泵输出压力,室内模拟试验出浆口到压力输入口存在管路压力的沿程损失; 2)脉动注浆过程中,脉动压力的停止泵送在数值模拟中可以实现净值为0,但在实验中存在残余压力; 3)室内模型试验的尺寸与存数值模拟和理论计算存在差异,导致边界条件和初始值不同,且注浆试验环境、试验操作等诸多因素有关,是一个十分复杂的过程,难以与理论完全一致。

5 结 论

(1)基于脉动注浆周期压力输出特性,考虑宾汉姆流体类浆液的屈服应力与黏度时变性,多孔介质渗滤效应,及地层参数的不确定性,依托COMSOL Multiphysics平台,结合MATLAB开发了适用于模拟脉动注浆扩散的程序; 基于脉冲泵注浆原理,在阀前后会产生压降,推导了适用于计算脉动注浆工艺工程应用的浆液运移扩散距离实用方程。

(2)根据脉动注浆周期压力输出原理,自制了一套试验室脉动注浆模拟试验装置,实现了渗滤效应下的脉动注浆扩散的模拟,得到了脉动周期压力和稳压施工参数下,浆液的渗滤扩散形态。结果表明,全风化花岗岩体中,稳压注浆存在明显的劈裂浆脉,浆液的扩散对土体的劈裂效应明显; 脉动注浆能够形成有效的加固圈与浆泡,且脉动注浆的扩散对于多孔介质充填率更高。

(3)理论分析、数值模拟与室内试验所得浆液扩散趋势一致、运移距离相近; 室内试验数据得出的浆液扩散形态与数值模拟计算的浆液扩散形态一致。研究结果表明,脉动压力控制下,浆液的扩散均匀,稳压注浆更易产生浆脉。研究结论为脉动注浆工艺进一步实现工程应用,提供了较强的理论指导。