偶变元严格几乎最优弹性布尔函数的High-Meets-Low 构造*

王飞鸿, 孙玉娟, 董雪雯, 张卫国

1.西安电子科技大学 空天地一体化综合业务网全国重点实验室, 西安710071

2.武汉船舶通信研究所, 武汉430200

1 引言

布尔函数在对称密码学中具有极为重要的作用, 如流密码中的伪随机数生成器、分组密码中的S 盒、Hash 函数等都可以通过适当的非线性布尔函数的组合来设计.布尔函数的安全性指标是衡量其密码学性质好坏的依据.在流密码设计中被广泛接受的布尔函数安全性指标主要有: 平衡性、适当阶数的相关免疫性、高非线性度、高代数次数、高代数免疫阶、高快速代数免疫阶等, 这些指标反映了密码抵抗各种类型攻击的能力.例如, 在流密码系统设计中, 为了抵抗最佳仿射逼近攻击[1], 布尔函数应具有高非线性度; 为了抵抗相关攻击[2], 布尔函数应具有适当阶数的相关免疫性[3].平衡性是设计用于密码场景的布尔函数时需满足的基本性质.同时具有平衡性和相关免疫性的布尔函数, 称之为弹性函数.平衡的t阶相关免疫函数, 称为t阶弹性函数.非线性度为Nf的n元t阶弹性布尔函数f, 在本文中简称为(n,t,Nf) 函数.

布尔函数的弹性阶和非线性度之间存在较强的制约关系, 较早指出存在这种制约关系的学者是Meier等人[4]与Ding[1].上世纪80 年代中期以来, 如何构造高非线性度的弹性布尔函数是一个重要的研究课题[5–21], 弹性布尔函数的非线性度的紧上界是尚未解决的公开难题.

本文给出了在偶数个变元情形下严格几乎最优弹性布尔函数的HML 构造方案, 并描述了两例参数分别为(22,4,221−210−29) 和(30,4,229−214−212) 的弹性函数的构造细节, 说明了由本文方法所得函数的参数可以优于文献[10] 中由GMM 构造法所得函数的参数.

本文其余部分安排如下: 第2 节介绍了布尔函数及HML 构造的相关知识; 第3 节给出偶变元严格几乎最优的弹性布尔函数的HML 构造方案;第4 节给出了(22,4,221−210−29)函数和(30,4,229−214−212)函数的构造细节, 并与文献[10] 中的结果进行比较; 第5 节总结全文.

2 预备知识

2.1 布尔函数

n元布尔函数定义为从Fn2到F2的一个映射.令Bn表示所有n元布尔函数构成的集合.用F2上的一个长为2n的向量

且形如式(1)的表示形式存在且唯一, 称该表示形式为f的代数正规型, 其中λI ∈F2,X=(x1,x2,···,xn)∈Fn2.f(X) 的代数次数是使得λI= 1 的最大|I| 值, 记为deg(f), 其中|I| 表示集合I的基数.若deg(f)≤1, 则称f是仿射函数.设ω= (ω1,ω2,···,ωn).将向量ω和X的内积记为:ω·X=ω1x1+ω2x2+···+ωnxn.显然,ω·X是常数项为0 的仿射函数.布尔函数f ∈Bn在ω点的Walsh 谱值定义为

则称f为严格几乎最优函数.

设n元布尔函数f(X) 中x1,x2,···,xn是 F2上均匀分布的独立随机变量, 若f(X) 与x1,x2,···,xn中任意t个变元统计独立, 则称f(X) 是t阶相关免疫函数.平衡的相关免疫函数称为弹性函数, 平衡布尔函数的相关免疫阶称为布尔函数的弹性阶.文献[22] 给出弹性函数的频谱特征, 这一结论被称为Xiao-Massey 定理.

引理1[22](Xiao-Massey 定理) 布尔函数f ∈Bn是t阶弹性函数当且仅当对任意ω ∈Fn2, 0≤wt(ω)≤t, 都有Wf(ω)=0.

下面介绍一种在HML 等构造法中需要使用到的重要工具: 残缺Walsh 变换.

定义2[15]设S是Fn2上的非空真子集,X ∈S.称函数fS:S →F2是S上的n元残缺布尔函数.fS在ω ∈Fn2点的残缺Walsh 变换定义为

若有序多重集WfS={FWfS(ω)|ω ∈Fn2}中元素是按ω的字典序排序的, 则称WfS为fS的残缺Walsh 谱.

残缺Walsh 谱有两条重要性质, 见引理2 和3.

则有

引理 3[15]设f和fSi是引理2 中定义的函数, 若对任意的ω ∈Fn2, 0≤wt(ω)≤t, 总有FWfSi(ω)=0,i=1,2,···,d成立, 则f是t阶弹性函数.

直和构造是一种基本的布尔函数构造方法, 由直和构造所得函数的弹性阶满足如下关系:

是s+m元t1+t2阶弹性函数.

证明: 设α ∈Fs2,β ∈Fm2.由公式(2)可知Wh(α,β)=Wc·X(α)·Wg(β).由wt(c)=t2,易知c·X是t2−1 阶弹性函数, 又g是t1阶弹性函数.注意到wt(α,β)=wt(α)+wt(β), 故当0≤wt(α,β)≤t1+t2时, 必有0≤wt(α)≤t2−1 或0≤wt(β)≤t1.由引理1, 有Wc·X(α) = 0 或Wg(β) = 0.从而Wh(α,β)=0, 即h(X,Y) 是一个s+m元t1+t2阶弹性函数.

2.2 HML 构造法描述

文献[15]中基于PW 函数(或KY 函数)给出奇数个变元的非线性度严格几乎最优弹性函数的HML构造方案.由于构造方案中需要在向量空间的不同划分上构造残缺布尔函数, 我们给出例1 便于读者理解这种“划分”.下面描述基于PW 函数的HML 构造法.

其中{U1,U2,U3,U4}是F152的一个划分.并统计Fu2×Uj中汉明重量不小于t+1 的向量个数, 其中j=1,2,3,u ≥0, 即

3 偶变元严格几乎最优弹性函数HML 构造的一般性结论

文献[11] 中给出的一种偶变元高非线性度1 阶弹性函数的构造方法, 这些函数的非线性度非常接近bent 函数的非线性度,这是1 阶弹性函数目前所能达到的最高非线性度.因此我们选取它作为偶数个变元的HML 构造中的初始函数, 并根据引理4 修改集合T1的取值范围为T1={η|wt(η)≥t −1,η ∈Fk2},实现了偶变元的严格几乎最优弹性函数的HML 构造, 下面给出该构造的一般性结论.

设g ∈Bm是由文献[11] 构造的m元1 阶弹性函数(m ≥8 且为偶数), 其Walsh 谱取值有

同时成立.从而可以分别建立从Ei到Ti的单射Φi, 其中i= 1,2,3,4.设X= (x1,x2,···,x2k)∈F2k2及Y ∈Fm2, 分别在Si上构造四个n元残缺布尔函数:

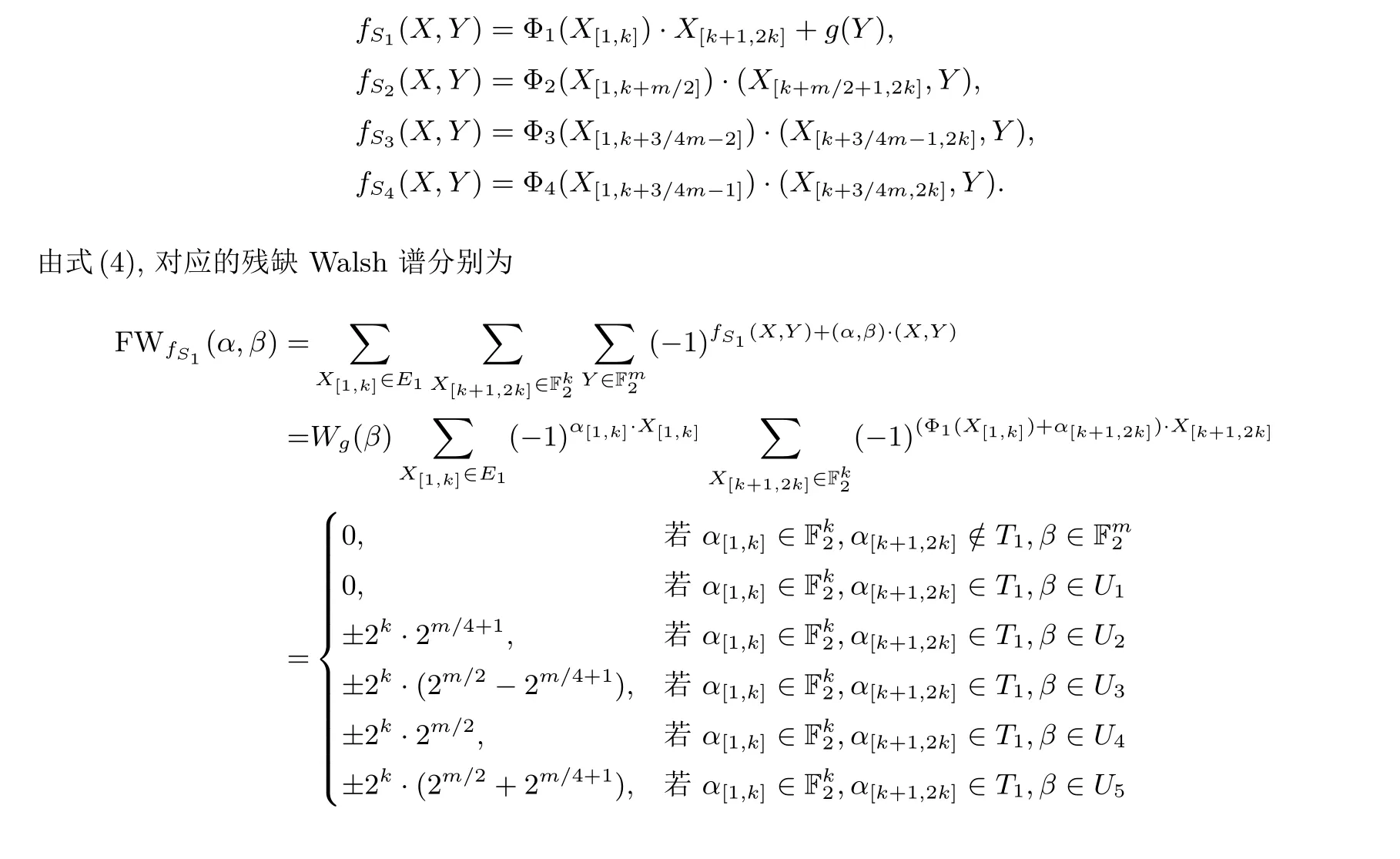
由引理3,f是t阶弹性函数.由式(5)得

成立, 则存在(n,t,2n−1−2n/2−1−2n/2−2) 严格几乎最优弹性函数.

定理2 对g ∈Bm, 在m ≥10 且m ≡2 mod 4 时, 有

证明: 与定理1 的证明相似.

4 两例高非线性度弹性布尔函数的具体构造

为了便于读者理解, 下面给出(22,4,221−210−29) 函数和(30,4,229−214−212) 函数的构造细节,并与文献[10] 中的结果进行比较.

4.1 (22,4,221 −210 −29) 函数的构造

首先选取一个文献[11] 中构造的1 阶弹性函数g1∈B8, 其真值表的16 进制表示为

注意到集合U4中向量对应的Walsh 谱振幅值与其它三个集合U1,U2,U3中向量对应的Walsh 谱振幅值间差值的二进制展开分别是: 24−0=24+23, 24−8=24, 24−16=23.这些差值中有两种2 的幂决定了F222被划分为三个集合S1,S2和S3.

第一步: 在S1上构造22 元残缺布尔函数fS1.

根据引理4, 由于所构造函数的弹性阶是4, 把F72中重量不小于3 的向量作成集合T1, 即

由引理4 及T1的定义有

第二步: 在S2上构造22 元残缺布尔函数fS2.

首先统计F82中使函数g1的Walsh 谱振幅值分别为0, 8 和16 时重量为τ的向量个数, 其中0≤τ ≤8, 即

表1 中列出了函数g1对应的Nj(τ) 值,j=1,2,3.

表1 函数g1 的Nj(τ) 值, j = 1,2,3Table 1 Nj(τ) for g1 function, j = 1,2,3

从而对任意u ≥0, 式(6)中Γj(u,t) 的数量为

由式(6),T2中的向量都不小于5.由式(15)得

第三步: 在S3上构造22 元残缺布尔函数fS3.

令

相应地, 由式(15)得

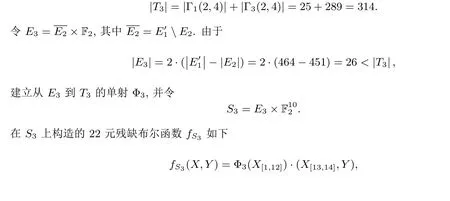
fS3的残缺Walsh 谱为

由定义1, 函数f为严格几乎最优函数.

与由文献[10] 中GMM 构造法得到的函数比较见表2.在非线性度相同的前提下, 本文中构造的22元严格几乎最优布尔函数的弹性阶更优.

表2 严格几乎最优布尔函数的弹性阶和非线性度比较Table 2 Resiliency and nonlinearity comparison of strictly almost optimal functions

通过该构造可以得到一个(22,4,221−210−29) 弹性函数, 其真值表见文献[23], 读者可自行验证其4 阶弹性和Walsh 谱分布的正确性.

4.2 (30,4,229 −214 −212) 函数的构造

通过文献[11] 构造的一个1 阶弹性函数g2∈B12, 其真值表见附录, 其Walsh 谱振幅值分布如下

其中U1∪U2∪U3∪U4∪U5=F122且Ui ∩Uj=∅对任意的1≤i ＜j ≤5 成立.由引理1 知, 其Walsh谱还满足

注意到集合U5中向量对应的Walsh 谱振幅值与其它四个集合U1,U2,U3,U4中向量对应的Walsh 谱振幅值间差值的二进制展开分别是: 80−0 = 26+24, 80−16 = 26, 80−48 = 25, 80−64 = 24.这些差值中有三种2 的幂决定了F302被划分为四个集合S1,S2,S3和S4.

相应地, 统计了F122中使函数g2的Walsh 谱振幅值分别为0, 16, 48 和64 时重量为τ的向量个数,其中0≤τ ≤12, 即

表3 中列出了函数g2对应的Nj(τ) 值,j=1,2,3,4.

表3 函数g2 的Nj(τ) 值, j = 1,2,3,4Table 3 Nj(τ) for g2 function, j = 1,2,3,4

从而对任意u ≥0, 式(6)中Γj(u,t) 的数量为

其中v=min{t,12},λ=min{u,t −τ}.分别令

与由文献[10] 中GMM 构造法得到的函数比较见表4.

表4 严格几乎最优布尔函数的弹性阶和非线性度比较Table 4 Resiliency and nonlinearity comparison of strictly almost optimal functions

在弹性阶相同的前提下, 本文中构造的30 元严格几乎最优布尔函数的非线性度更优.

5 结论

自上世纪80 年代中期, 如何构造高非线性度的弹性布尔函数一直是一个重要的研究课题, 文献[15]引入了“残缺布尔函数” 和“残缺Walsh 变换” 的概念, 提出HML 密码函数构造法, 首次使奇数个变元的弹性布尔函数的非线性度大幅提高到2n−1−2(n −1)/2+5·2(n−11)/2.本文推广该构造技术至偶数个变元的情形, 实现了偶变元严格几乎最优的弹性布尔函数的HML 构造方案, 构造出了非线性度为2n−1−2n/2−1−2n/2−m/4和2n−1−2n/2−1−2n/2−(m/2−1)/2(m ≥8 且为偶数) 的严格几乎最优弹性函数, 并给出两个具有目前已知最高非线性度的弹性函数的例子, 其参数分别为(22,4,221−210−29) 和(30,4,229−214−212).