基于可分性改进分组密码SM4 和FOX 的积分区分器*
2024-01-11毛永霞吴文玲
毛永霞, 吴文玲
1.中国科学院 软件研究所 可信计算与信息保障实验室, 北京100190
2.中国科学院大学, 北京100049
3.河南师范大学 数学与信息科学学院, 新乡453000
1 引言
积分分析是由Knudsen 等人[1]在FSE 2002 上提出来的.由于它首先被应用于分组密码Square[2],因此也被称为Square 攻击.它是当前评估分组密码算法安全性的基础分析方法之一, 已经在许多分组密码算法上得到了较好的攻击结果, 例如AES[3]等.可分性是积分分析的推广, 在EUROCRYPT 2015 上被Todo[4]首次提出.Todo 结合密码算法非线性部件的代数次数, 优化了积分性质, 使得积分特征能够用一种更精确的方式推导.一个显著的应用是第一次在理论上对全轮的MISTY1 进行了积分攻击[5].后来, Todo 等人[6]在FSE 2016 上又提出了更精细的比特级可分性(bit-based division property, BDP).在ASIACRYPT 2016 上, Xiang 等人[7]将基于混合整数线性规划(mixed integer linear programming,MILP) 建模的方法引入比特级可分性, 进一步提高了积分区分器可自动化搜索的密码算法的规模.2017年, Todo 等人[8]对上述MILP 模型进行了补充, 并将其应用于多个流密码算法的立方攻击, 得到了几个流密码当时最好的密钥恢复攻击.近几年, 对分组密码算法的积分区分器搜索的改进主要围绕改进非线性层[9,10]和线性层[11–15]的可分性传播模型来进行.
SM4[16]是由国家密码管理局于2006 年1 月发布的分组密码, 专为无线局域网标准设计, 2016 年被采纳为国家标准, 2021 年被纳入ISO/IEC 国际标准, 自发布以来一直是许多密码分析者攻击的目标.在积分分析方面, 2007 年, Liu 等人[17]利用特定的差分对和S 盒性质, 构造了SM4 的8 轮积分区分器.2012 年, Zhang 等人[18]对高阶积分分析的概念进行扩展, 并提出了一种由内而外搜索高阶积分区分器的方法, 构造了256 个Gen-SM4 结构的10 轮区分器.2015 年, Sun 等人[19]利用在特定条件下零相关线性壳与积分区分器的存在性之间具有某种关系, 构造了SM4 的12 轮积分区分器.2018 年, Eskandari 等人[20]利用可分性构造了12 轮的积分区分器.后来, 胡西超[21]提高了12 轮积分区分器的数据复杂度.
FOX[22]是一个分组密码算法族, 应MediaCrypt AG 公司的要求而设计, 在各种平台上使用时具有高灵活性和高实现性能的特点.它包含FOX64 和FOX128 两个密码算法, 分别具有64 比特和128 比特的分组长度: 每一个分组密码又支持不同的密钥长度, 具有不同的轮数.FOX 的整体结构是Lai-Massey结构, 轮函数是SPS 结构, 设计者证明了它对线性和差分分析是免疫的.2015 年, Qiao 等人[23]结合MILP 技术给出了更紧的差分活跃S 盒个数的下界.同年, 伊文坛等人[24]给出了FOX 的多维零相关线性分析.由于FOX 整体结构比较复杂, 目前已有的最长积分区分器是设计文档给出的三个FOX64 的3轮积分性质.设计文档声称4 轮FOX64/64、5 轮FOX64/128、6 轮FOX64/192、7 轮FOX64/256、5轮FOX128 对积分攻击免疫, 但是Wu 等人[25,26]结合碰撞技术和积分攻击改进了对FOX 的积分攻击结果, 发现4 轮FOX64/64、5 轮FOX64/128、6 轮FOX64/192、7 轮FOX64/256、5 轮FOX128/256对积分攻击均不免疫.
本文的贡献如下.分支异或压缩结构和非比特置换的线性变换是分组密码的两个基本部件.本文通过分析可分性在这两个部件上传播的特点, 分别提出了两个建模策略.策略一通过增加约束条件维持部分输入可分性经过首轮传播的状态, 使得这部分可分性在后续传播中更有优势; 策略二通过增加约束条件提高可分性经过线性变换传播时的模型精度, 提高可分性传播的效率.将两个建模策略分别应用于分组密码SM4 和FOX, 可以构造SM4 的13 轮积分区分器、FOX64 的3 轮积分区分器、FOX128 的3 轮积分区分器(表1 展示了与已有积分区分器的结果对比).这些区分器都优于相应密码算法已知的最好积分区分器.

表1 SM4 和FOX 已有积分区分器的结果对比Table 1 Integral distinguisher results for SM4 and FOX
本文剩余的内容安排如下: 第2 节为预备知识, 主要介绍符号约定、可分性相关定义和建模规则;第3 节介绍针对两种密码部件提出的自动化方法的建模策略; 第4 节介绍两个策略在分组密码SM4 和FOX 上的应用; 第5 节是本文总结.
2 预备知识
2.1 符号和定义
对于一个分组密码, 用下面的符号表示明文半字节和密文半字节的积分性质:
-C: 明文半字节的每一个比特都是常数;
-A: 明文半字节的每一个比特都是活跃的;
-B: 密文半字节的每个比特都是平衡的;
-U: 密文半字节的状态是未知的.

2.2 可分性和可分迹
定义1 (比特级可分性[6]) 设X 是一个取值于Fm2的多重集,k ∈Fm2.当多重集X 有可分性D1,mK时, 满足下面的条件:

2.3 结合自动化建模技术与比特级可分性搜索积分区分器
自动化搜索技术已经成为构造分组密码区分器的主要方法, 借助数学工具提高搜索能力和效果是目前最流行的方法之一.利用SAT (satisfiability modulo theories)、MILP (mixed integer linear programming) 等数学工具搜索可分性在分组密码上的传播是目前构造积分区分器最常用的方法.这两种数学工具的建模方式相似, 都是通过刻画可分性在密码基本部件上的传播, 设置合理的目标函数, 将可分性传播的搜索问题转化为一个SAT 或MILP 问题.然后借助合适的求解器如Cryptominisat 或Gurobi 对模型进行求解, 最后根据求解结果和可分性判断条件判断是否存在积分区分器.下面简要介绍基于MILP 的建模过程.

(1) 二元运算的建模规则
在基于比特的可分性传播中, 文献[4] 证明了可分性在5 种密码基本部件上的传播规则.本节介绍其中的两种, 即可分性传播在COPY 函数和XOR 函数(如图1–2) 上的MILP 建模规则.

图1 COPY 函数Figure 1 COPY

图2 XOR 函数Figure 2 XOR
(2) S 盒的建模规则

例1 设S 是一个3 比特S 盒, 如表2 所示, (u,v) 表示可分迹uS−→v, 可求得如下17条可分迹: (0,0,0,0,0,0), (0,0,1,0,0,1), (0,0,1,0,1,0), (0,0,1,1,0,0), (0,1,0,0,0,1), (0,1,0,0,1,0),(0,1,0,1,0,0), (0,1,1,0,1,1), (0,1,1,1,0,0), (1,0,0,0,0,1), (1,0,0,0,1,0), (1,0,0,1,0,0), (1,0,1,0,1,0),(1,0,1,1,0,1), (1,1,0,0,0,1), (1,1,0,1,1,0), (1,1,1,1,1,1).

表2 一个3 比特S 盒Table 2 A 3-bit S-box
Step 1 写出S 盒可分迹对应的真值表, 并将其导入Logic Friday;
Step 2 生成描述S 盒所有不可能可分迹对应点的析取范式并进行约简;
Step 3 转化成合取范式f=(u1+(v1+1)+(v0+1))(u0+(v1+1)+(v0+1))···;
Step 4 合取范式包含18 个因式,f为真当且仅当所有因式为真.因此每一个因式对应一个不等式.例如, 因式u1+(v1+1)+(v0+1) 对应不等式u1+(v1+1)+(v0+1)≥1.以此类推, 写出所有不等式.这18 个不等式就刻画了比特级可分性在S 盒上的传播.
3 自动化分析方法的两种有效建模策略
辅助数学工具的自动化分析方法的建模策略非常重要, 它会直接影响模型的中间状态和求解空间, 也决定着模型的精度, 因此经常会影响可分性的搜索结果.目前, 尽管基于自动化建模方法描述可分性传播的技术已经非常成熟, 但实际中往往会产生误报, 即输出可分性为单位向量的可分迹的存在性并不能确保该输出位置的积分区分器不存在.正如Derbez 等人所说[28], 可分性的核心是追踪单项式通过迭代函数的传播, 而误报是因为在追踪过程中没有恰当地处理异或操作导致的.例如, 设p和q是两个包含变量x的多项式,p=xp1⊕p2,q=xq1⊕q2.尽管p和q都依赖变量x, 但是p ⊕q是不清楚的.为了保持建模过程简单, 通常假设p ⊕q在定义1 的可分性下仍旧依赖变量x.显然, 这种假设有时候并不正确.在分组密码的轮函数中, 非比特置换的线性层部分通常包含最多的异或运算.为了降低异或运算因为建模方式带来的误差, 提高可分性传播模型的精度, 许多密码学者提出了针对线性层建模的改进方法[11–15].本节针对两种包含异或操作的密码部件: 分支异或压缩结构和非比特置换的线性变换, 分别提出了基于模型的中间状态和基于模型的精度进行改进的建模策略.
3.1 策略一: 针对分支异或压缩结构的建模
Feistel 结构一轮的扩散速度通常没有SP 结构一轮的扩散速度快, 因此需要更多的轮数保证相同水平的安全强度.为此, 密码设计者有时候将整体采用Feistel 结构的分组密码的输入分支经过异或压缩处理,例如Gen-SM4 结构(图3).类似地, 安全强度看起来更高的Lai-Massey 结构也包含分支异或压缩部件(例如图4).在传统构造积分区分器的方法中, 密码分析者通常将参与异或压缩的分支选择相同的明文结构, 从而确保经过一轮迭代之后, 压缩输出的分支是非活跃状态, 进而使得初始输入状态可以传播得更远,最终达到获得更优积分区分器的目的.受此启发, 我们对具有这类密码部件的分组密码建立可分性传播模型时, 采用深度优先的建模策略, 即为异或压缩的参与分支的输入可分性添加约束条件, 舍弃一部分有效可分迹, 只保留经过该结构之后输出活跃位置最少的可分性状态, 从而达到可分性具有更优传播效果的目的, 具体过程如策略一所述.

图3 SM4 的一轮变换Figure 3 Round function of SM4
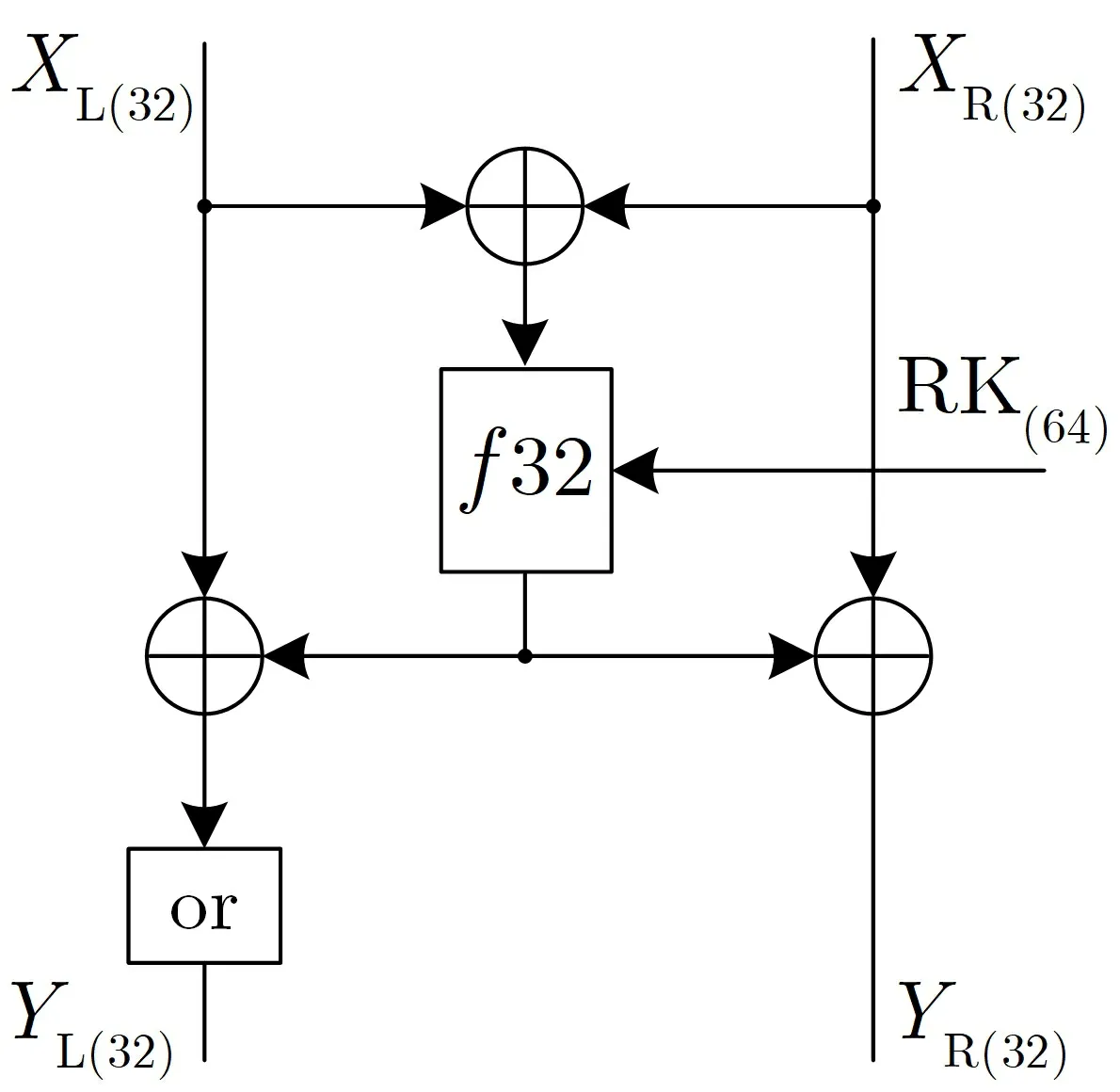
图4 FOX64 的一轮变换Figure 4 Round Function of FOX64

图5 FOX128 的一轮变换Figure 5 Round Function of FOX128
策略一: 设密码算法的轮函数包含t个输入分支参与异或压缩, 每个分支长度为n比特, 异或压缩函数F⊕: (Fn2)t →Fn2描述为(X1,X2,···,Xt)⊕−→Y.这t个分支第i比特对应的可分迹记为(a1i,a2i,···,ati)→bi, 0≤i ≤n −1.那么在第一轮的可分性传播模型中添加如下约束条件
基于自动化建模方法搜索积分区分器时, 需要对初始输入状态的活跃情况进行遍历, 以期找到可分性传播最优的情况.受到计算复杂度的制约, 这在实际中往往是不可行的.根据可分性的传播特点, 初始输入可分性汉明重量越大, 一般传播得也越远.为此, 许多攻击者通常将初始可分性设置为一比特是常数,其余比特均活跃, 以此寻找最长的积分区分器.例如, 文献[29] 提出了优化的积分区分器搜索算法: 先判断一比特常数下积分区分器的存在性, 再降低活跃比特数, 找到最优的积分区分器.对于包含分支异或压缩的密码结构来说, 这种策略或许并不是最优的(4.1 节证实了这种猜测).策略一根据密码算法的结构特点, 对初始输入可分性进行限制, 即异或压缩的输入分支之间的可分性是相互制约的, 它们满足关系a1i+a2i+···+ati= 0.并且, 这一约束条件保证了压缩输出的分支是不活跃的, 因为它对应的可分性bi= 0.换言之, 通过策略一删除经过异或压缩结构的部分可分迹, 使得被保留的可分迹满足条件: 当异或压缩输出分支作为中间状态的输入时, 中间状态可分性的汉明重量不会因为异或压缩结构而降低.
3.2 策略二: 针对非比特置换线性变换的建模
分组密码轮函数包含的非比特置换线性变换可以写成一个二元线性变换矩阵.那么, 利用COPY/XOR 函数建模规则可以对任意维数的线性变换矩阵直接建立可分性传播的约束模型.正如文献[30] 指出, 由于非独立活跃比特的影响, 这种建模方式得到的约束会产生冗余可分迹, 进而导致可分性传播提前终止.文献[30] 提出了一种减少冗余可分迹、提高模型精度的建模方法.该方法的核心思想是通过处理线性变换矩阵消除非独立活跃比特.

文献[30] 中的算法1 和算法2 描述了对矩阵建模的过程.其中, 算法1 对矩阵的行之间进行两两配对, 找到两行之间非独立可分性传播比特(输出结果记为result), 算法2 对矩阵M涉及的非独立可分性传播进行处理: 通过引入新的中间变量TN, 将矩阵拆分为独立建模的COPY 矩阵和XOR 矩阵.经过观察发现,TN在建模过程中作为一个整体参与COPY/XOR 运算, 因此没必要再拆分开单独建立约束, 只需要整体进行约束即可.为此, 我们给出文献[30] 中关于TN的等价约束条件, 即策略二.

根据传统COPY 函数和XOR 函数的建模规则, 策略二中非独立可分性传播部分建立的可分性约束条件为:

结合COPY 约束条件, 这与不等式(1)显然是等价的.
设j1,j2∈result, 根据文献[30] 中的算法2, 将这条非独立可分性传播转化为独立可分性传播需要在MILP 模型中添加对应如下约束的不等式条件
这意味着, 若TN在bj1的可分性取1, 那么在bj2必定取0; 若TN在bj1的可分性取0, 那么在bj2必定取1.这与不等式(1)显然也是等价的.
此外, 策略二的另一个优点是: 无需对矩阵M提前进行行配对, 以期找到最多的公共变量个数(文献[30] 的算法1), 只需要对任意包含非独立可分性传播的两行添加如不等式(1)的约束条件即可, 需要添加的不等式个数上界为m(m −1)/2.算法1 描述了利用策略二对M建模的过程.其中, 3–6 行对矩阵M涉及的非独立可分性传播进行处理, 第5 行的a=(a1,a2,···,an) 代表可分性向量.

算法1.构建线性变换的BDP 传播的新MILP 模型Input: 线性变换矩阵M Output: M 对应的BDP 传播模型M 1 建立空的MILP 模型M;2 生成输入/输出/中间变量M.var ←ai,bi,ui;3 for i ̸= j,(i,j) ∈(0,m)×(0,m),t ∈(0,n) do 4 l =(l0i ∧l0j,l1i ∧l1j,··· ,lni ∧lnj);5 M.con ←〈a,l〉 ≤1;6 end 7 for j ∈(0,n),i ∈(0,m) do 8 M.con ←aj = ∑n−1 k=0 uk ·M [i][j];9 end 10 for i ∈(0,m),j ∈(0,n) do 11 M.con ←bi = ∑n−1 k=0 uk ·M [i][j];12 end 13 return M.
4 应用于SM4 和FOX
4.1 应用于SM4
SM4 整体采用广义Feistel 结构, 分组长度和密钥长度均为128 比特, 加密轮数为32 轮.SM4 的一轮变换如图3 所示, 第i轮轮函数F定义为F(Xi,Xi+1,Xi+2,Xi+3,RKi) =Xi ⊕T(Xi+1⊕Xi+2⊕Xi+3⊕RKi), 0≤i ≤31.其中, 合成置换T是一个32 维的可逆变换, 由非线性变换τ和线性变换L复合而成, 即T(.)=L(τ(.)).非线性变换τ由4 个并置的8 比特S 盒构成, 线性变换L表示如下:
其中,B ∈Z322是输入,C ∈Z322是输出.明文经过32 轮加密之后, 最后再经过一个反序变换R输出密文.设Y0,Y1,Y2,Y3为输出, 那么(Y0,Y1,Y2,Y3)=R(X32,X33,X34,X35)=(X35,X34,X33,X32).
不考虑最后一个反序变换, 利用MILP 方法建模, 搜索SM4 的积分区分器.首先, 根据第2 节S 盒的建模规则, 利用Logic Friday 软件, 共得到191 个约束不等式描述可分性在SM4 的8 比特S 盒上的传播.由于线性变换比较简单, 可以根据二元运算的建模规则直接对其建立约束条件.然后, 设置初始输入的一比特为常数, 其余比特全活跃.最后, 借助Gurobi 求解器对模型进行求解.遍历输入的常数位置, 得到如下结果: 输入最低32 位任一位为常数, 其余位置全活跃, 12 轮传播之后存在32 个平衡比特(最高32位), 而13 轮之后无平衡位置.采用3.1 节的策略一, 增加首轮关于分支异或压缩结构的约束条件:
其中,a1i,a2i,a3i分别表示输入分支X1,X2,X3第i比特的可分性.这可以构造13 轮的积分区分器: 选择初始输入最低32 位任一位为常数, 其余位置全活跃, 13 轮传播之后存在32 个平衡比特.例如, 选取最后一比特为常数, 那么可以构建如下13 轮SM4 的积分区分器:
4.2 应用于FOX
FOX 支持两种分组长度: 64 比特和128 比特, 密钥k的长度满足0≤k ≤256, 且是8 的倍数, 轮数r随着密钥长度的改变而不同.FOX64 和FOX128 的一轮变换如图4–5 所示.下面介绍FOX64 的轮函数f32、FOX128 的轮函数f64、以及or 函数.
(1) 轮函数f32f32 是FOX64 的核心函数, 输入输出都为32 比特, 包含三个部分: 替换部分sigma4、扩散部分mu4 和轮密钥加部分,如图6 所示.设f32 的输入输出分别为X(32)和Y(32),64 比特的轮密钥为RK(64)=RK0(32)||RK1(32), 那么Y(32)=sigma4(mu4(sigma4(X(32)⊕RK0(32)))⊕RK1(32))⊕RK0(32).非线性变换sigma4 由4 个并置的8 比特S 盒组成, 线性变换mu4 可以写成GF(28)上的一个4×4 的变换矩阵.

图6 f32Figure 6 f32
(2) 轮函数f64f64 是FOX128 的核心函数, 类似于f32, 输入输出都为64 比特, 也包含三个部分: 替换部分sigma8、扩散部分mu8 和轮密钥加部分, 如图7 所示.设f64 的输入输出分别为X(64)和Y(64),128 比特的轮密钥为RK(128)= RK0(64)||RK1(64), 那么Y(64)= sigma8(mu8(sigma8(X(64)⊕RK0(64)))⊕RK1(64))⊕RK0(64).非线性变换sigma8 由8 个并置的8 比特S 盒组成(S 盒与f32 相同), 线性变换mu8 可以写成GF(28) 上的一个8×8 的变换矩阵.
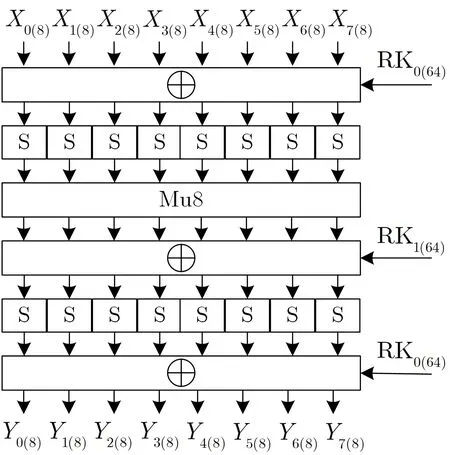
图7 f64Figure 7 f64
(3) or 函数or 函数是一轮Feistel 变换, 输入输出均为32 比特.设输入为X(32)=X0(16)||X1(16), 那么输出Y(32)=Y0(16)||Y1(16)=X1(16)||(X0(16)⊕X1(16)).FOX64 和FOX128 的最后一轮都不包含or函数, 即, 最后一轮的or 变换相当于一个恒等变换.
根据第2 节S 盒的建模规则, 利用Logic Friday 软件, 共得到614 个约束不等式描述可分性在FOX的8 比特S 盒上的传播.针对FOX64, 采用3.1 节的策略一, 增加首轮关于分支异或压缩的约束条件:

5 总结
本文针对分组密码的分支异或压缩结构和非比特置换的线性变换, 提出了两种自动化建模策略: 策略一对初始输入可分性进行约束, 从而保证经过首轮分支异或压缩结构的输出可分性为0, 使得可分性传播更有优势; 策略二通过对线性变换中的非独立可分性传播比特进行约束, 减少冗余可分迹, 提高模型的精度; 并且, 将两种策略分别应用于分组密码SM4 和FOX, 改进了二者关于积分区分器搜索的结果.因为这两种策略都是基于分组密码的结构提出的, 因此本文的建模策略不仅适用于基于MILP 技术搜索可分性, 也适用于基于SAT/SMT 等技术搜索可分性.
