基于地统计空间插值的三维辐射场重构研究
2024-01-11龙泽宇宋佩涛冯青靓李华韦加富刘瑞文牛瑨博
龙泽宇, 宋佩涛, 冯青靓, 李华, 韦加富, 刘瑞文, 牛瑨博
(1. 中国辐射防护研究院 辐射安全与防护山西省重点实验室, 太原, 030006;2. 中国辐射防护研究院 国家环境保护辐射环境与健康重点实验室, 太原, 030006;3. 中国辐射防护研究院 核与辐射前沿技术研究中心, 太原, 030006)
0 引言
在核设施退役工作中,工作人员通常需要直接进入到高剂量照射的辐射区域中进行作业,准确获取区域内的辐射场分布,不仅可以精准有效地指导工作方案的具体规划,还能通过辐射剂量可视化等手段,消除工作人员对辐射“看不见,摸不着”的恐慌心理,对工作人员的辐射防护最优化有现实意义。
通常,获取辐射场的方法可分为基于辐射源项的正演计算方法和基于辐射测量数据的插值计算方法两大类。正演计算是指根据放射源及场景信息,直接计算辐射场的剂量率分布[1];插值计算方法,则是在利用固定或移动式测量设备获取的离散辐射测量数据基础上,利用插值算法实现整个辐射区域剂量场的重构。基于辐射测量数据的插值计算方法仅依赖于实测的辐射剂量率数据,不需要掌握具体的辐射源项信息,适用性要优于正演计算方法。
中国工程物理研究院赛雪利用MQ径向基函数散乱数据插值法,实现了只有少量不规则分布的剂量数据下的辐射场重构及可视化[2],但其所建立的模型还较为简单,仅适用于两种简单情况下的辐射场重构。哈尔滨工程大学的李梦堃提出了一种核设施退役辐射场剂量分布仿真方法[3],该方法根据样本数据,先构建径向基神经网络模型,然后通过反距离权重法计算核设施退役剂量场中任意一点的剂量值,最后计算出辐射场的剂量率分布,但实验结果表明,只有对于均匀分布的数据,插值结果才较好。南华大学张敏提出了一种利用辐射剂量值占优构造还原算法对已知探测点的剂量进行外插和内推的方法[4],重新构造出了完整的平面辐射场,但是重构得到的辐射场的准确度主要取决于探测点的数量,当测点数量较少时,重构的准确度较低。
地统计插值技术起初是从研究矿产储量计算问题而产生并发展起来的,但凡是要研究空间分布数据的自相关性,并对这批数据进行最优无偏插值估计时,均可应用地统计插值。辐射场本质上由是放射源发出的射线产生的,同样具有空间自相关性,距离越近的点剂量率就越接近,因此将地统计插值用于辐射场重构是非常合适的。地统计空间插值尽管都以克里金方法为核心,但其种类繁多,考虑到辐射场还具有变化梯度大的特点,本文尝试将普通克里金方法与对数变换相结合,在离散测量点的基础上进行辐射场重构,并利用实测辐射场对其进行验证,为源项未知情况下的三维辐射场获取提供一种新方法。
1 方法原理
1.1 普通克里金方法
克里金法的实质是利用区域化变量的观测点数据,对插值点的数据进行无偏估计,其中应用最为广泛的为普通克里金方法[5-6]。在普通克里金方法中,对于一个插值点的数据采用观测点数据的线性组合来估计:
(1)
式中,Z*(x0)为插值点数据的估计值;Z(xi)为观测点的数据;λi为权重系数,表示各观测点对插值点估计值的贡献程度,其求解必须满足2个条件:线性无偏和使估计方差最小,分别见式(2)和式(3):
E[Z*(x0)-Z(x0)]=
(2)
(3)
式中,X=Z*(x0)-Z(x0)。
对于式(2),由于普通克里金方法假设空间任意点都有同样的期望,即E[Z(x)]=c,可得:
(4)
对于式(3),要使估计方差最小,根据拉格朗日乘数法,可得:
(5)
式中,μ为拉格朗日乘数;ri,j为半方差函数(见1.2节)。对式(4)和式(5)进行求解,获得权重系数λi,代入式(1),即可获得插值点数据的估计值。
1.2 半方差函数及对数变换
半方差函数ri,j反映了区域化变量的变异程度,其计算公式见式(6):
(6)
普通克里金方法假设ri,j与两点之间的距离di,j存在着函数关系,因此只需计算出观测数据集中各点间的距离di,j和半方差ri,j,再寻找一个半方差拟合模型来拟合出两者的关系,即可根据插值点和观测点间的距离,计算出式(5)中的ri,0。
常用半方差拟合模型包括Linear、Power、Gaussian、 Spherical、Exponential等5种,分别见式(7)、式(8)、式(9)、式(10)、式(11):
r(d)=sd+n
(7)
r(d)=sdω+n
(8)
(9)
(10)
(11)
用普通克里金方法进行插值估计时,一般要求数据服从正态分布。然而由于辐射剂量遵循平方反比定律,各点处的剂量率值会在远离源项的方向迅速下降,因此整个辐射场的剂量率值分布通常呈正偏态分布,直接使用普通克里金法来进行插值,结果的偏差可能会较大。
对此,本文在插值前先对观测点数据进行对数变换,以使其更接近正态分布:
Z′(xi)=lnZ(xi)
(12)
在对各观测点数据进行对数变换,并利用普通克里金方法进行插值后,将各点插值结果按式(13)再进行一次逆变换,作为最后的插值点估计值:
Z*(x0)=eZ*′(x0)
(13)
式中,Z*′(x0)为直接使用经对数变换处理的观测数据获得的插值点估计值;Z*(x0)为经过逆变换后最终的插值点估计值。
需要说明的是,考虑到辐射场具有各向同性的特点,因此本文不对各轴向进行拉伸处理。另外当测量点数量较多,且分布范围较大时,为了避免离插值点距离过远的观测点对插值结果产生不利影响,可只采用离插值点距离最近的部分观测点参与计算。
2 随机选点情况下的测试验证
2.1 测试验证一
为验证方法在三维辐射场重构上的有效性和可靠性,在某厂房中选取了一放置有废物桶的房间进行现场测量实验。使用全站仪以及长杆式剂量率仪对废物桶周围的辐射场进行测量,剂量率仪测量辐射场中某一点的剂量率值,全站仪记录该点对应的坐标,使坐标与剂量率值一一对应,得到相应的辐射场数据,总数为150个点,其三维建模如图1所示。

图1 测试验证一的三维建模图
对所有的已知点进行随机选取,选取数量分别为总数的15%(23个点)、20%(30个点)和25%(38个点),重复次数为5 000次,将选取到的点作为测量点,剩余的点作为辐射场重构的验证点,在不同半方差拟合模型下重构结果的平均偏差分别列于表1、表2、表3(此处的平均偏差为单次随机选点在各验证点处重构结果偏差的平均值,而表中的最大值、最小值、平均值为5 000次随机选点的平均偏差中的最大值、最小值、平均值,下同)。
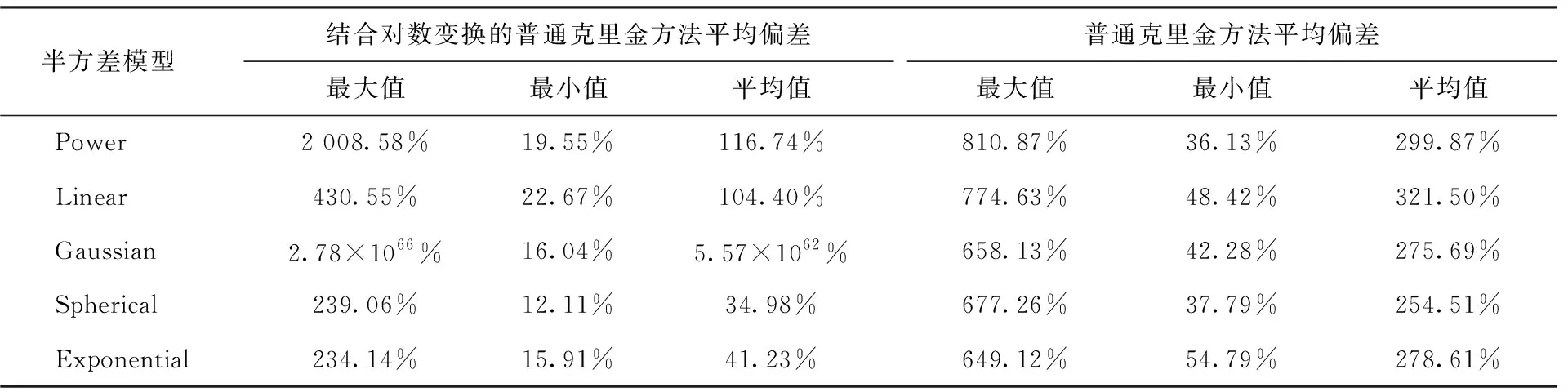
表1 测试验证一中测量点数量为23情况下的重构结果平均偏差
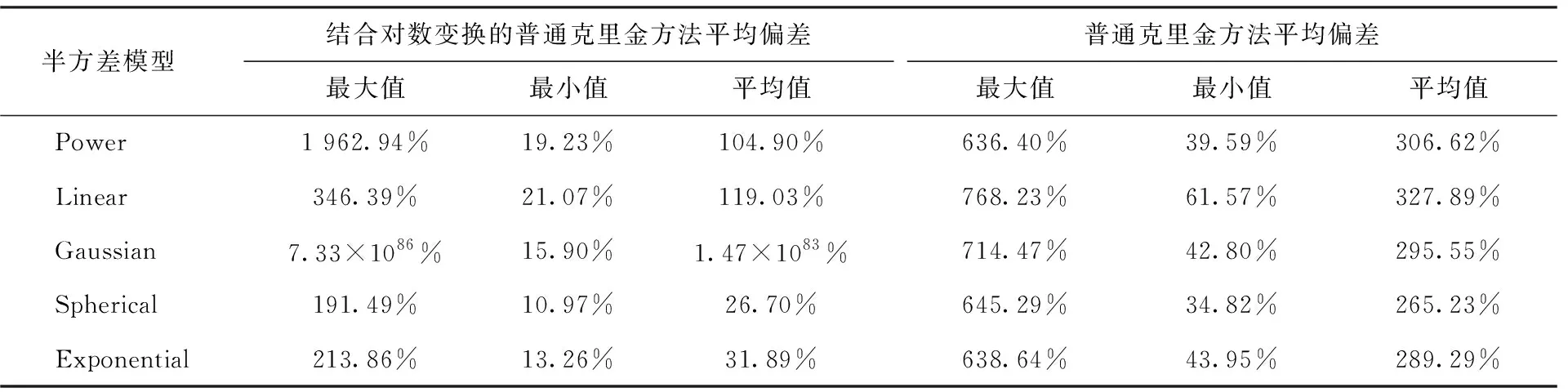
表2 测试验证一中测量点数量为30情况下的重构结果平均偏差
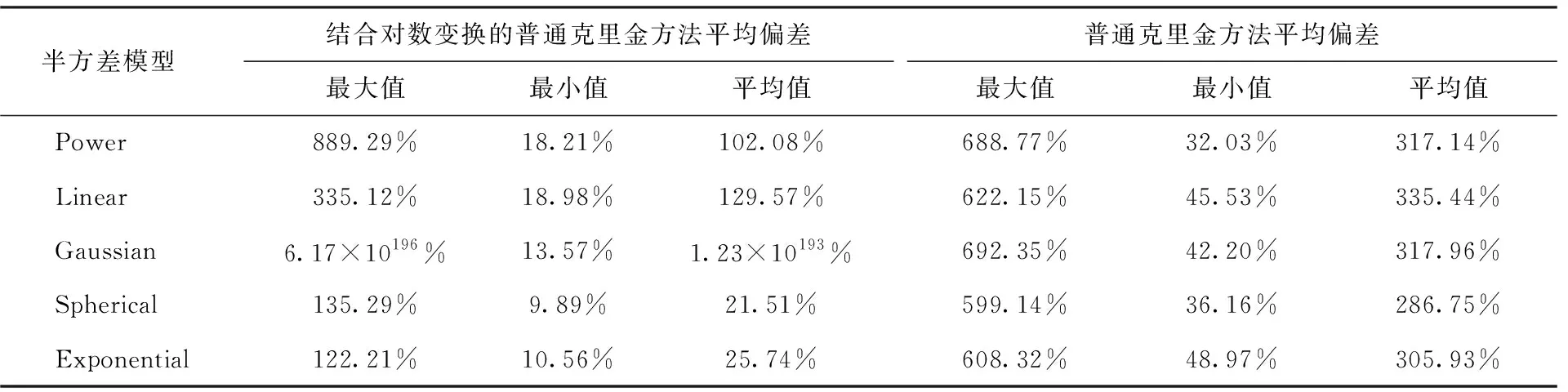
表3 测试验证一中测量点数量为38情况下的重构结果平均偏差
由表1、表2、表3可见,若以5 000次随机选点测试的重构结果平均偏差的平均值作为评判标准,普通克里金方法在结合对数变换后,在除Gaussian之外的模型上,重构结果的准确度均有较大提升。其中,Exponential模型和Spherical模型的准确度要相对更优,在测量点数量为23、30、38时,分别为41.23%、31.89%、25.74%和34.98%、26.70%、21.51%。
2.2 测试验证二
测试验证二的场景相对更为复杂,场景中存在某大型设施作为屏蔽物,剂量率已知点散布在该设施周围,总数为46个,其三维建模如图2所示。

图2 测试验证二的三维建模图
同样对所有的已知点进行随机选取,选取数量分别为总数的15%(7个点)、20%(10个点)和25%(12个点),重复次数为5 000次。将选取到的点作为测量点,剩余的点作为辐射场重构的验证点,在不同半方差拟合模型下重构结果的平均偏差分别如表4、表5、表6所示。

表4 测试验证二中测量点数量为7情况下的重构结果平均偏差
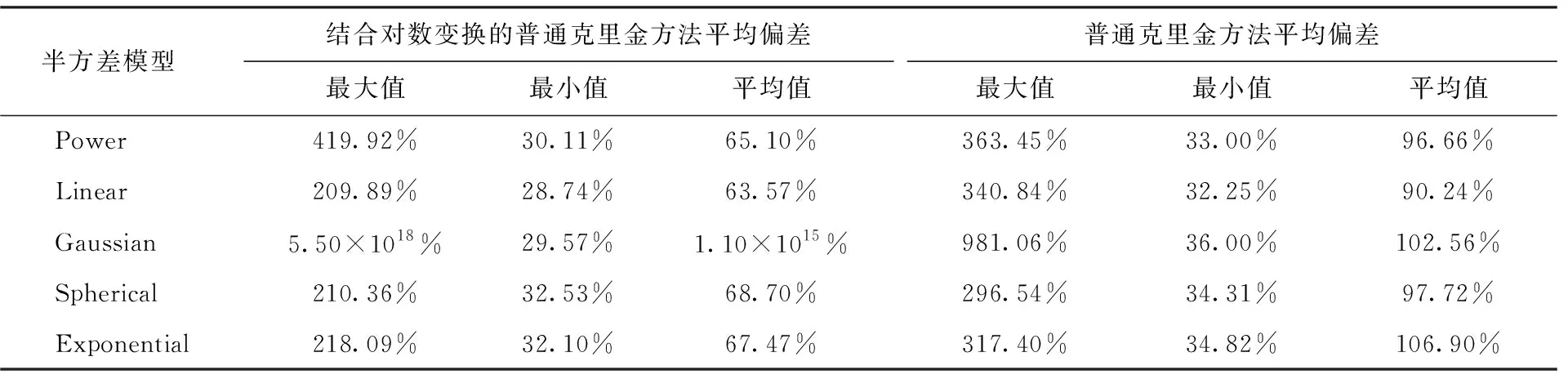
表5 测试验证二中测量点数量为10情况下的重构结果平均偏差
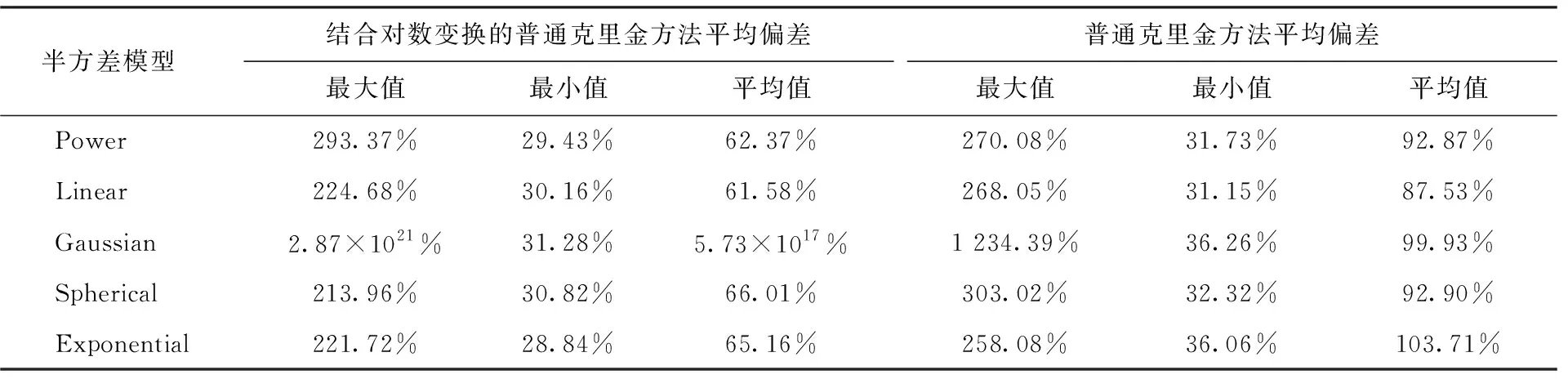
表6 测试验证二中测量点数量为12情况下的重构结果平均偏差
由表4、表5、表6可见,在测试验证二中,普通克里金方法在结合对数变换后,在除Gaussian外的模型上,重构结果的准确度同样均有提升。但与测试验证一不同的是,在测试验证二中除Gaussian外的4种模型的重构准确度都较为接近,在测量点数量为7时,平均偏差的平均值为70.07%~74.01%;在测点数量为10时,平均偏差的平均值为63.57%~68.70%;在测点数量为12时,平均偏差的平均值为61.58%~66.01%。
2.3 综合结果
综合测试验证一和测试验证二的结果,对于结合对数变换的普通克里金方法,半方差拟合模型可选用在测试验证一和测试验证二中都表现较好的Exponential模型或Spherical模型,在随机选点的情况下,其重构结果平均偏差的平均值范围为21.51%~74.01%。
此外,对于同样数量的测量点和同样的半方差拟合模型,重复选点测试中的最大平均偏差和最小平均偏差存在数量级的差异,说明测量点选取情况对重构结果准确度的影响较大。因此,为了给实际工程应用中的测量点选取工作提供指导,确保结合对数变换的普通克里金方法在辐射场重构上的准确性,还必须对测量点的较优选取方案进行研究。
3 测量点选取方案
考虑到克里金方法本身的空间插值特性,本文从测量点分布的均匀性出发,分析其和辐射场重构准确性之间的关系,从而确定出一种合适的测量点选取方案。为对测量点分布的均匀性进行量化,本文采用文献[7]中的公式对其进行计算:
(14)
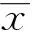
测量点数目越多,其均匀性的量化就越准确。本文选取测试一中测量点数目为38,且半方差拟合模型为Exponential和Spherical的实验数据为研究对象,按照式(14)进行计算,绘制的散点图如图3所示。
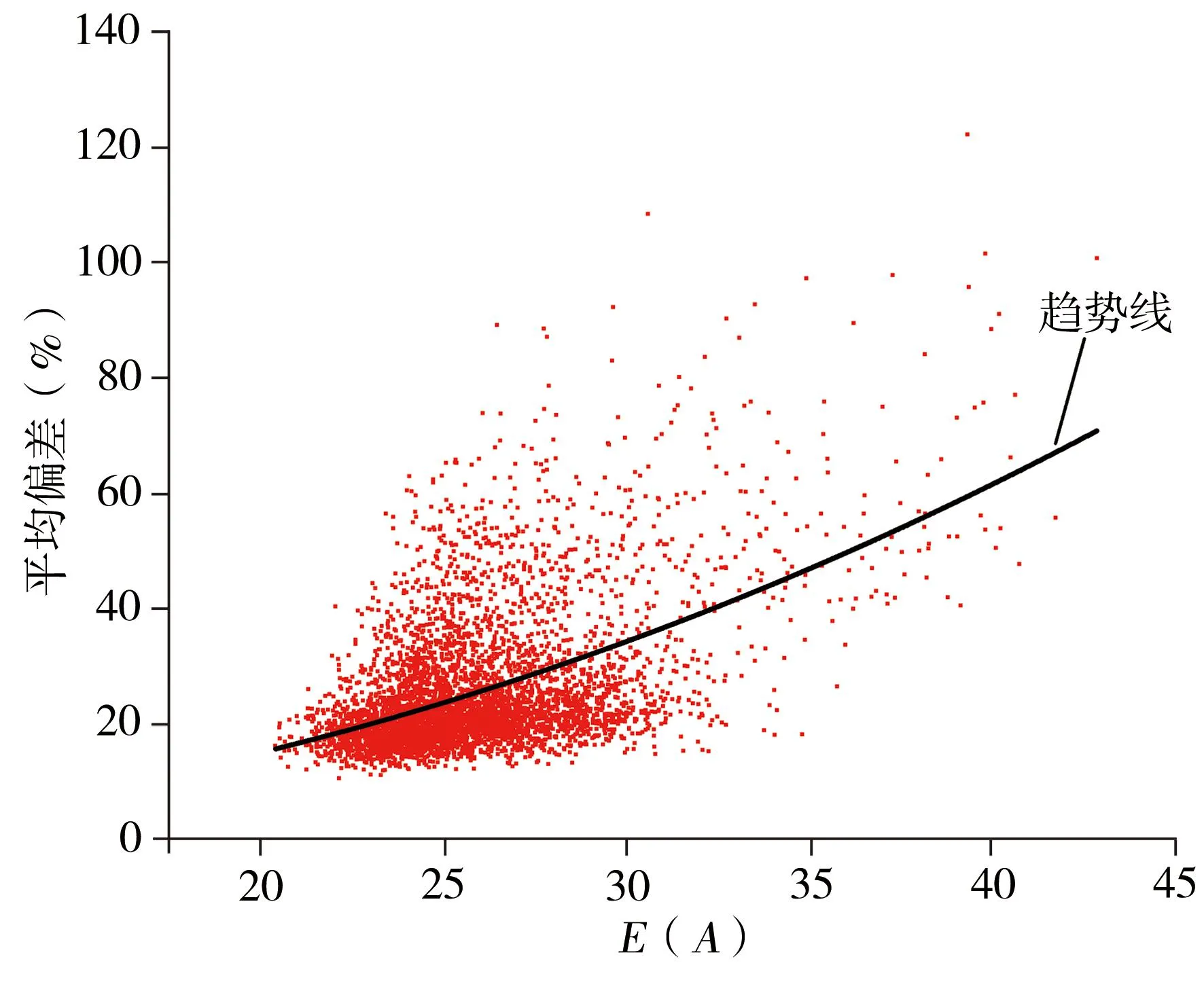
(a) Exponential模型
由图3可见,当采用结合对数变换的普通克里金方法进行三维辐射场重构时,无论是采用Exponential模型还是Spherical模型,测量点分布的均匀性都和辐射场重构的准确性存在一定的正相关性。因此为了确保辐射场重构的准确性,应用中测量点分布应尽可能的均匀。
4 结语
本文对地统计空间插值中结合对数变换的普通克里金方法进行了介绍,并通过2个实测的辐射场数据对该方法进行了测试验证。测试验证结果表明,该方法在选取Exponential模型和Spherical模型为半方差拟合模型,且测量点为随机选取的情况下,其重构结果平均偏差的平均值处于21.51%~74.01%的范围,显示出该方法在实际应用中具备一定的可行性。同时对测量点选取与重构准确性之间的关系进行了初步分析研究,确定了测量点分布应尽可能均匀的选取方案。
