基于FDS的真实火灾下钢管约束钢筋混凝土柱抗火性能

杨冬冬, 万鹏程, 王 琨, 王烨淳

(扬州大学建筑科学与工程学院, 江苏 扬州 225127)

钢管约束钢筋混凝土(steel tubed reinforced concrete, STRC)柱是一种新型高性能组合构件, 由薄壁钢管和钢筋混凝土组成, 具有承载力高、延性好、抗震性能优越和施工方便等优点[1], 被广泛应用于国内高层建筑和大跨场馆．由于STRC柱的钢管外露, 抗火性能是该类构件设计中的关键问题．已有学者对圆形、方形和矩形STRC柱在ISO 834系列标准火灾条件下的抗火性能展开了试验研究和理论分析[2-5], 提出了耐火极限和防火保护设计方法．真实火灾下, 结构的温度分布和力学性能与标准火灾场景存在较大差异[6-7], 基于标准火灾条件进行STRC柱的抗火设计可能不满足安全需求或过于保守, 因而, 开展真实火灾场景下STRC柱的抗火性能研究具有重要的现实意义．采用火灾动力学模拟(fire dynamics simulator, FDS)软件可获取不同真实火灾场景下的升温曲线进行柱构件的抗火性能研究．如段进涛等[8]采用FDS分析了真实火灾下钢结构的力学性能, 建议进行钢构件稳定分析时考虑热膨胀引起的温度内力; 樊华等[9]对比了ISO 834标准火灾条件与基于FDS的真实火灾条件下钢管混凝土柱的耐火性能, 结果表明真实火灾下构件耐火极限较大; 崔志强等[10]认为火灾升温速率越慢, 钢管混凝土组合柱在真实火灾中的抗火性能越好．

本文拟选取宿舍和教室作为火灾场景, 采用FDS获取相对真实的室内升温曲线, 通过Abaqus软件开展真实火灾场景下圆形STRC柱的温度场和耐火极限有限元分析, 揭示真实火灾对构件抗火性能的影响, 提出STRC柱的抗火设计建议．

1 基于FDS的真实火灾曲线

1.1 FDS模型构建

宿舍和教室均为人流密集、财物集中的公共场所, 防火安全设计格外重要．本文选取宿舍与教室两处典型场所, 采用FDS建立如图1所示的火灾场景模型．宿舍长宽高分别为6.6, 3.6, 3.0 m, 通风口为一扇门(2.4 m×0.9 m)和两扇窗(1.3 m×1.2 m), 燃烧物为四张上床下桌的组合书桌(长1.9 m, 宽0.9 m, 桌高0.8 m, 床高1.9 m)．教室长宽高分别为6.8, 6.0, 3.0 m, 通风口为两扇门(2.2 m×0.8 m)和四扇窗(1.2 m×1.1 m), 燃烧物包括讲台(1.3 m×0.4 m×1.3 m)和四排课桌椅(0.7 m×0.5 m×0.9 m)．参考文献[9,11]的数据, 燃烧物热释放速率取1 500 kW·m-2, 其他火灾参数取FDS数据库内的推荐数值．

图1 宿舍(a)和教室(b)火灾场景示意Fig.1 Illustration of dormitory(a) and classroom(b) fire scenarios

1.2 真实火灾曲线生成

宿舍和教室共设置6种工况和燃烧模式, 如表1所示．火灾场景设置27个热电偶, 平均分布于如图1所示的模型中高0.1, 1.5, 2.9 m的3个Oxy平面上, 分别命名为平面1～3．宿舍场景中热电偶沿x轴间距3.2 m、沿y轴间距1.7 m分布; 教室场景中热电偶沿x轴间距2.9 m、沿y轴间距3.4 m分布, 边缘距墙0.1 m．以平面1热电偶编号为例: 宿舍或教室场景中远离原点沿x方向依次为a1～c1, 近原点沿x方向依次为d1～f1, 中间沿x方向依次为g1～i1．

表1 火灾工况及其燃烧模式

采用FDS计算得到各火灾场景下不同平面处的温度-时间曲线, 以如图2所示的宿舍Ⅱ结果为例, 图2结果表明: 真实火灾下,不同平面处测点的温度均呈现较为复杂的发展趋势, 存在明显的上下浮动．火灾发生初期, 可燃物开始燃烧释放大量热量, 导致室内温度迅速升高; 火灾后期, 由于可燃物类型较为单一, 且数量相对有限, 热量释放进入相对稳定阶段,环境温度逐渐趋于平缓．由于室内热烟气整体向上流动, 平面1～3的温度分布规律明显不同, 平面高度越低,不同测点间的温度差异越显著．平面1中, 远离火源的f1测点平稳段温度最低, 仅约200 ℃, 而位于宿舍中心的h1测点的温度则高达700 ℃．对于离地最高的平面3, 各测点的平稳段温度较为均匀, 在450～650 ℃之间变化．

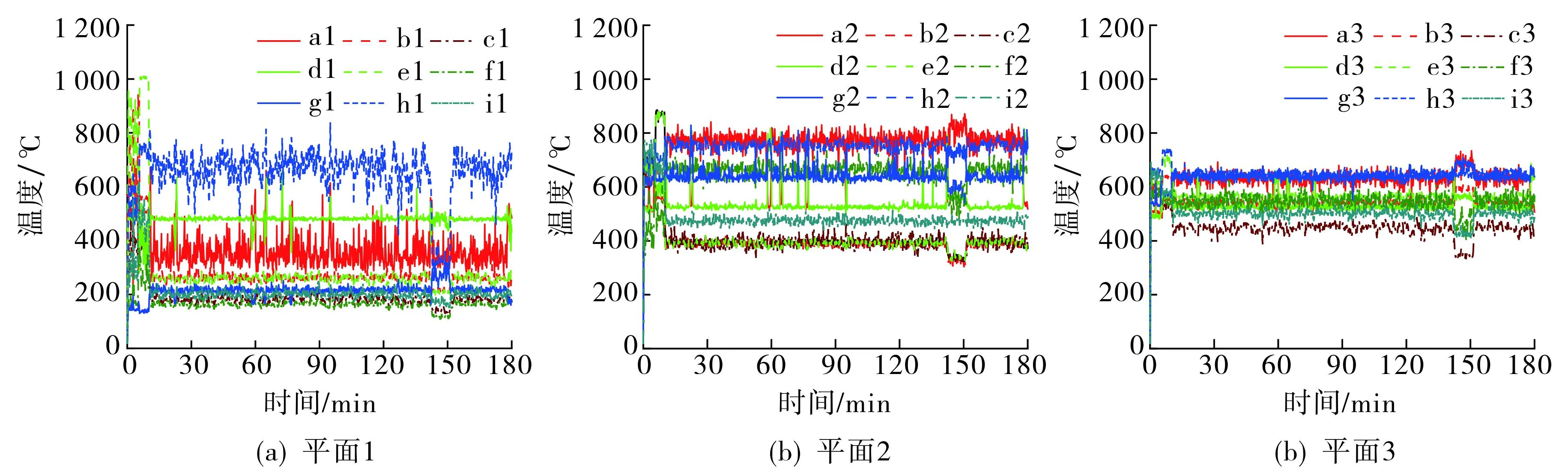
图2 宿舍Ⅱ工况下不同平面处的温度-时间曲线Fig.2 Temperature-time curves at different planes in Dormitory Ⅱ scenario

本文6种工况下的火灾温度最高测点分别为h2,a2,a2,b3,i1,i1, 以上测点的温度-时间曲线如图3所示．由图3可见, 由于真实火灾中可燃物数量和氧气含量等相对有限,在3 h的火灾全过程中, 其最高温度低于相同升温时刻ISO 834标准火灾的温度．除教室Ⅱ中选用的i1测点因距离起火位置较远,前期升温速率较低外, 真实火灾在初始阶段的升温速率和温度均高于标准火灾．由于教室Ⅰ场景选用的温度测点b3靠近燃烧物且位于离地最高的平面3,其在升温30 min内的温度基本都高于标准火灾,可能对耐火极限较小的STRC柱耐火性能的影响较大．

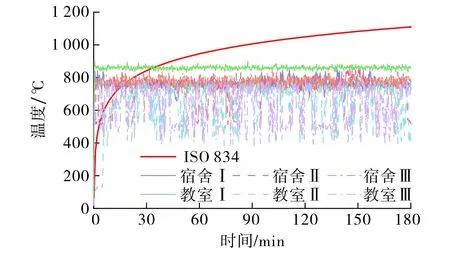
图3 真实火灾场景与ISO 834标准场景下的温度-时间曲线对比Fig.3 Comparison of temperature-time curves between real fire scenarios and ISO 834 fire condition

2 有限元模型建立及验证

采用Abaqus中顺序热力耦合方法建立STRC柱温度场和耐火极限模型, 二者网格划分一致, 由于几何结构和载荷等具有对称性, 故采用1/4模型进行分析．高温下混凝土的热工参数、热膨胀系数、应力-应变关系等参考文献[12]的取值, 钢管和钢筋的热膨胀系数和应力-应变本构则采用EC3模型[13]．温度场模型中钢管表面对流系数取25 W·(m2·K)-1, 综合辐射系数取0.7, 钢管与混凝土间的接触热阻取0.01 m2·K·W-1, 钢筋与相应位置混凝土节点绑定, 混凝土、钢管和钢筋分别采用DC3D8、DS4和DC1D2单元．耐火极限模型中混凝土与钢管采用面-面接触, 切向为库伦摩擦, 摩擦因数取0.3, 法向为硬接触, 钢筋内置于混凝土, 对称面设置对称边界, 柱顶混凝土设置为刚性面, 边界条件和轴向载荷施加在参考点, 仅允许单向转动和轴向平动, 采用1/1 000柱长的一阶屈曲模态作为初始缺陷．混凝土、钢管和钢筋的单元类型分别为C3D8R、S4R和T3D2．通过12个STRC柱的截面温度、轴向位移、侧向位移、破坏模式和耐火极限等试验数据对本文建立的模型进行了验证[2-5], 该模型可用于真实火灾下STRC柱的抗火性能分析．

3 抗火性能分析与讨论

选取直径200 mm、长细比30、配筋率3.56%、含钢率3.36%、混凝土强度等级C50、钢管牌号Q355、钢筋牌号HRB400的STRC柱为典型算例, 计算真实火灾下构件的温度分布、轴向位移、侧向位移和耐火极限, 然后分析各主要参数对真实火灾下STRC柱耐火极限的影响规律．对于真实火灾场景和标准火灾场景, 均取STRC柱的轴向变形达到0.01L(L为柱长, mm)或变形速率达到每分钟0.003L的升温时间为耐火极限[2-5]．

3.1 温度场分析

图4为不同火灾场景下钢管、钢筋以及混凝土表面的温度-时间曲线．由图4可见, 真实火灾下钢管温度的变化规律与环境温度曲线类似, 存在明显上下波动, 升温20 min内, 除宿舍Ⅱ和教室Ⅱ外, 真实火灾下的钢管温度较标准火灾结果高; 真实火灾下混凝土和钢筋的温度均随时间平稳升高, 且一般较标准火灾下升温更慢．

图4 真实火灾下钢管(a)、钢筋(b)和混凝土(c)的温度时间曲线Fig.4 Temperature-time curves of steel tube(a), rebar(b) and concrete(c) under real fire

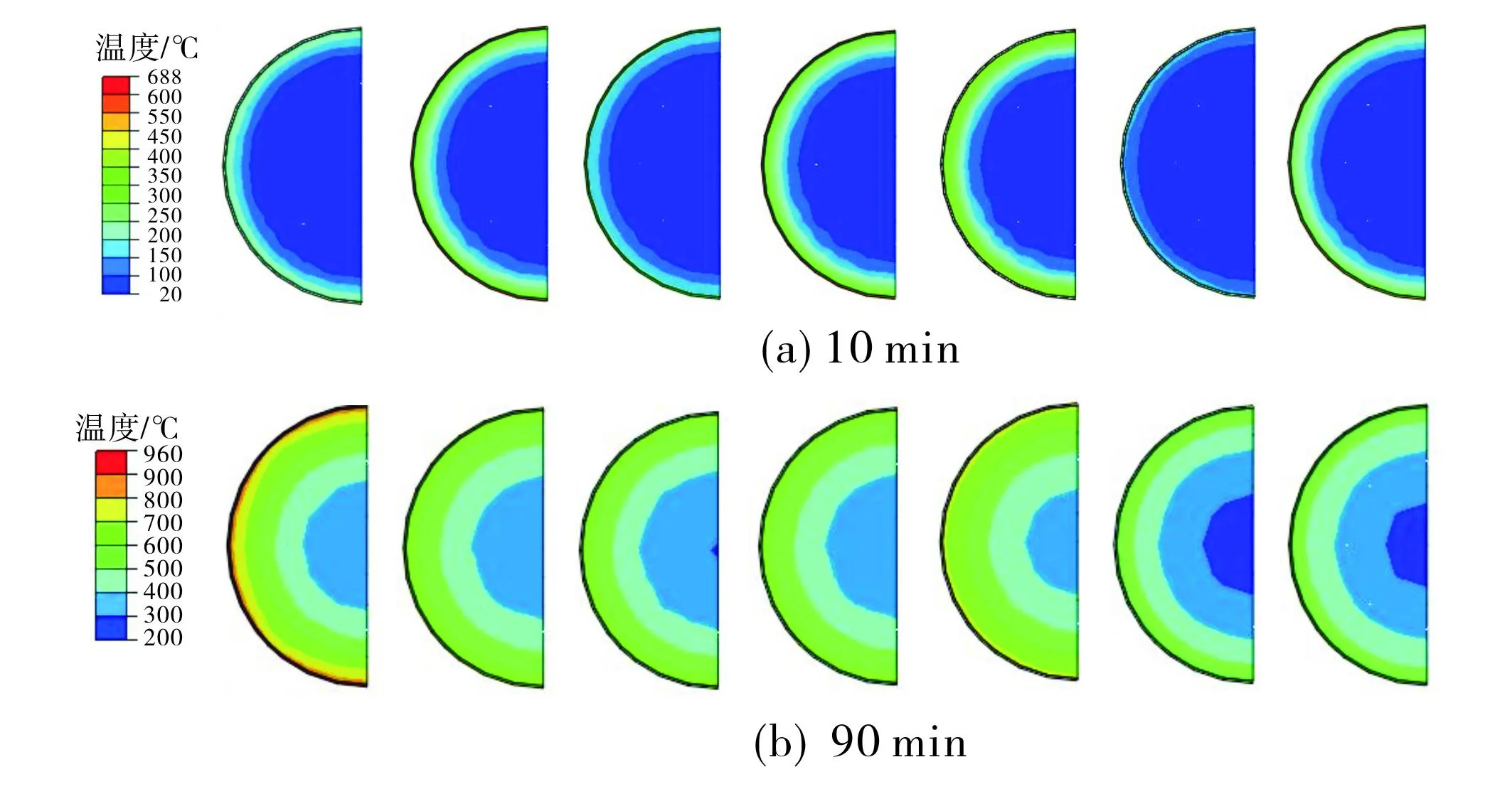
工况条件从左至右依次为ISO 834,宿舍Ⅰ,宿舍Ⅱ,宿舍Ⅲ,教室Ⅰ,教室Ⅱ,教室Ⅲ.图5 不同升温时刻构件截面温度分布Fig.5 Temperature distributions of STRC column section at different heating times

图5为升温10 min和90 min时不同火灾场景下构件的截面温度场．由图5可见: 真实火灾和标准火灾下构件截面温度分布规律类似, 升温初期, 整体温度均较低, 随时间增长, 内部低温区域占比逐渐减小．相同升温时刻, 不同火灾场景下构件截面温度及温度梯度存在显著差异．升温10 min时, 所有火灾场景中教室I的温度梯度最大且其外钢管温度最高, 达688 ℃(如图4(a)), 对应的钢管高温屈服强度折减系数为26%, 而宿舍Ⅱ和教室Ⅱ场景下的钢管温度均低于400 ℃,其屈服强度未发生折减; 升温90 min时, 真实火灾场景下的钢管温度与标准火灾的计算结果相比均更低, 但教室I场景下混凝土的最低温度为352 ℃, 高于标准火灾的相应结果326 ℃(如图4(c))．

3.2 变形行为分析

图6为各真实火灾场景下STRC柱的柱顶轴向位移-时间曲线和跨中侧向位移-时间曲线．图6中构件耐火极限设为STRC柱轴向变形速率超过4.5 mm·min-1时对应的升温时刻, 而柱构件一级耐火等级对应耐火极限为180 min, 故图6及后文中均仅给出构件破坏时间在180 min内的计算结果．由图6可见, 真实火灾下, 不同载荷比的STRC柱的破坏模式类似, 均因轴向变形速率超过规范限值而整体失稳．相同升温时间内, 柱顶轴向位移和跨中侧向位移及其相应的变化速率均随载荷比增大而明显增大．当载荷比为0.3和0.5时, 真实火灾下构件的轴向位移和侧向位移一般小于标准火灾的结果, 这是因为当升温时间相对较长时, 真实火灾下构件的截面温度一般较标准火灾场景低(如图4所示)．而当载荷比为0.7时, 除教室Ⅱ场景外,真实火灾下构件的高温变形均较标准火灾下的结果大, 这是因为此时构件破坏对应的升温时间较短, 小于20 min, 相同升温时刻真实火灾场景下构件的截面温度更高．

图6 真实火灾下轴向位移时间和侧向位移时间曲线Fig.6 Axial displacement-time and lateral displacement-time curves under real fire

图6数据显示, STRC柱的耐火极限随载荷比增大而减小, 这是因为火灾下构件的承载力随温度升高逐渐降低, 当其降低到与柱顶轴压载荷相等时, 构件达到耐火极限, 而载荷比越大, 施加在柱顶的轴向载荷越大, 构件越早失效破坏[3,4,14]．真实火灾的温度在升温30 min内一般高于标准火灾, 而在升温后期则均低于标准火灾(如图3所示)．载荷比为0.7的工况下, 构件破坏时对应升温时间较短, 因此真实火灾场景下的耐火极限一般较标准火灾结果更低; 而对于载荷比为0.3和0.5的工况, 构件破坏时的升温时间相对较长, 此时真实火灾下构件温度较低, 因此构件耐火极限较标准火灾场景更高．

3.3 关键参数影响分析

已有研究表明, 载荷比、长细比和截面尺寸是影响STRC柱抗火性能的主要参数[2,4,14], 故本文重点分析上述参数在真实火灾下对圆STRC柱耐火极限的影响．截面直径为200 mm, 长细比分别为30,45和60的构件在不同载荷比下的耐火极限如图7所示．由图7可见: 载荷比较大时, 真实火灾下与标准火灾下构件耐火极限相差较小; 而载荷比为0.3时, 除教室Ⅰ工况外, 真实火灾的耐火极限明显大于标准火灾．这是由于真实火灾温度在后期趋于平缓, 因此构件耐火极限随载荷比降低而增大的幅度较标准火灾工况更大．长细比为45时, 宿舍Ⅰ和标准火灾场景下, 载荷比由0.5减为0.3,耐火极限分别增大291%和206%．此外,教室I的空气温度在火灾工况中最高,且在升温30 min内均高于标准火灾, 因此该工况下耐火极限较低．图7还表明, 长细比越小, 真实火灾下构件的耐火极限相对较大, 载荷比对耐火极限的不利影响越显著．以教室Ⅲ场景为例, 长细比为60的工况下,载荷比由0.5增为0.7,耐火极限由25.4 min减小为2.4 min, 降低90.6%;而长细比为30时, 载荷比由0.5增为0.7, 耐火极限由150.1 min减小为3.4 min,降低97.8%．

图7 载荷比对真实火灾下STRC柱耐火极限影响Fig.7 Influences of load ratio on the fire resistance of STRC columns under real fire

图8为载荷比分别为0.3, 0.5, 0.7时长细比对STRC柱耐火极限的影响．图中未显示的数据点皆因其耐火极限超过180 min．由图8可见, 长细比越大, 耐火极限越小, 这是因为长细比越大, 二阶效应对构件抗火性能的不利影响越显著．以教室Ⅲ场景为例, 载荷比为0.5时, 长细比由30增大到45、60时,构件耐火极限由150 min分别降为72.4 min和27.9 min, 降幅分别为51.7%和81.4%．图8还表明, 载荷比越小, 长细比对耐火极限的不利影响越明显．以教室Ⅰ场景为例, 载荷比为0.3时, 长细比由30增大为60,构件耐火极限由113.5 min减小至36.8 min, 降低67.6%; 而当载荷比为0.7时,同等条件下耐火极限由1.67 min减为1.27 min,降低23.9%．

图8 长细比对真实火灾下STRC柱耐火极限影响Fig.8 Influences of slenderness ratio on the fire resistance of STRC columns under real fire

图9为载荷比不同时截面直径对STRC柱耐火极限的影响, 图中未显示载荷比为0.3及0.5时耐火极限超过180 min的计算结果．图9显示: 真实火灾下构件耐火极限随构件截面直径增大而增大, 这是因为构件截面直径越大, 混凝土的吸热效应越明显, 截面整体温度越低．载荷比越小, 增大截面直径对提高耐火极限的有利作用越明显．以教室Ⅰ场景为例, 载荷比为0.5时,截面直径由200 mm增大到1 000 mm, 构件耐火极限增大225%; 而载荷比为0.7时,耐火极限增幅仅为118%．

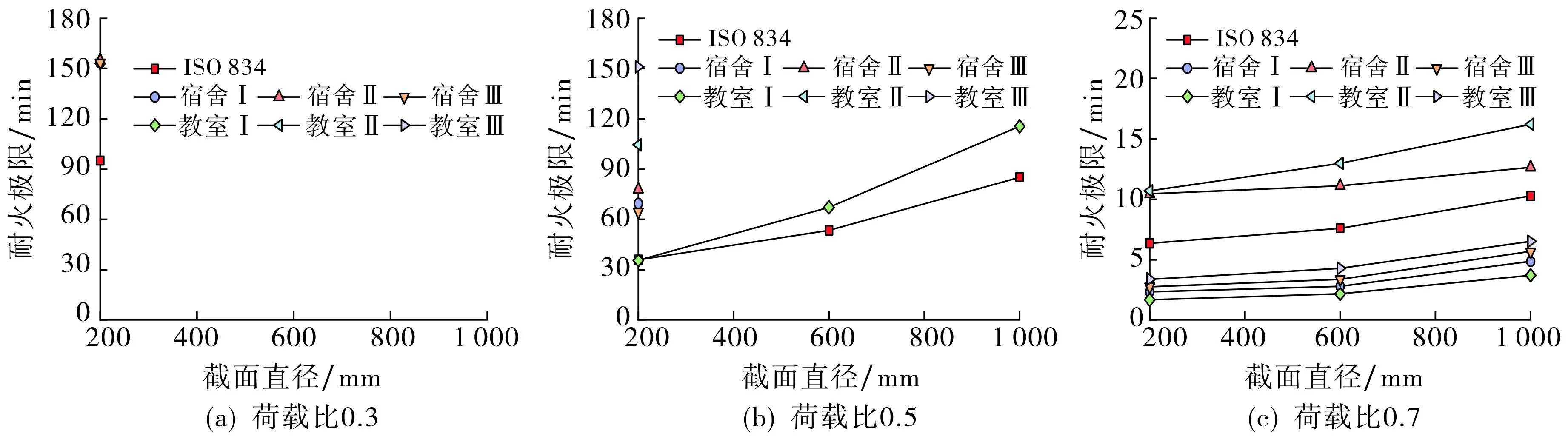
图9 截面直径对真实火灾下STRC柱耐火极限影响Fig.9 Influences of cross-sectional diameter on the fire resistance of STRC columns under real fire

3.4 耐火极限对比

对比图7～9中计算得到的真实火灾和标准火灾下构件的耐火极限可得, 6种火灾工况下的构件耐火极限与其标准火灾耐火极限的比值平均值分别为0.93, 1.42, 0.93, 0.69, 1.99, 1.66, 总比值平均值为1.23, 结果说明构件在真实火灾下具有更好的抗火性能．在真实火灾下构件耐火性能较差的少数情况发生在载荷较大、截面直径较小或长细比较大的工况中, 约占总算例数量的43.1%,此时构件耐火极限小于30 min, 真实火灾在相应升温时间内的温度较标准火灾更高(如图3所示)．而在工程范围内,如耐火极限超过60 min后, 真实火灾下构件耐火极限一般大于标准火灾的结果．因此,在本文选取的火灾工况和参数范围内,可出于安全考虑采用标准火灾进行STRC柱抗火设计．

为了进一步对比真实火灾和标准火灾条件下的耐火极限, 基于等效爆火时间的概念, 采用面积等效法[15], 将真实火灾下构件耐火极限转换为标准火灾下的等效耐火极限, 结果见表2．比较图7～9以及表2结果可知, 在真实火灾下计算耐火极限小于20 min的情况中(约占总算例的41.5%), 等效耐火极限较计算耐火极限大, 二者比值平均值为1.35; 在真实火灾的计算耐火极限大于20 min的情况中(约占总算例的58.5%), 等效耐火极限较计算耐火极限小, 二者比值平均值为0.79．为了进一步对比等效耐火极限与标准火灾耐火极限, 计算6种火灾工况下的等效耐火极限与其标准火灾耐火极限的比值平均值, 结果分别为0.91, 1.20, 0.92, 0.76, 1.29, 1.29,总比值平均值为1.05．耐火极限大于30 min时,等效耐火极限一般高于标准火灾耐火极限,可出于安全考虑按标准火灾基于等效爆火时间进行抗火设计,而耐火极限小于30 min时,真实火灾下的等效耐火极限更低,建议采用真实火灾进行结构抗火设计．

表2 真实火灾下STRC柱的等效耐火极限

4 结论

本文基于FDS获取了相对真实的火灾升温曲线, 开展了圆形STRC柱的抗火性能有限元分析, 得到以下结论: 1) 真实火灾在升温初期的升温速率和温度一般均高于ISO 834标准火灾, 但升温后期存在温度平缓段, 且温度低于标准火灾; 2) 真实火灾下圆形STRC柱的温度分布、变形行为和破坏失效等与标准火灾下结果类似, 构件耐火极限均与载荷比和长细比成反比, 与截面直径成正比; 3) 本文参数范围内, 单物体燃烧、引燃和共燃对应的6种真实火灾工况下, STRC柱的耐火极限与标准火灾下耐火极限的比值平均值分别为0.93,1.42,0.93,0.69,1.99,1.66, 而基于面积等效法得到的等效爆火时间与标准火灾耐火极限的比值平均值分别为0.91,1.20,0.92,0.76,1.29,1.29; 4) 不同真实火灾场景下构件的耐火极限存在较大差异, 工程实践中, 尤其是耐火极限小于30 min工况下, 建议采用真实火灾曲线进行STRC柱的抗火设计, 在工程常见耐火极限范围内, 当有可靠依据时, 可采用标准火灾曲线基于等效爆火时间进行构件抗火性能设计．

本文研究可为真实火灾工况下STRC结构的耐火验算、防火保护以及性能化抗火设计提供一定参考．今后还应建立不同火荷载、通风因子、墙面材料等参数下的真实火灾模型, 对真实火灾下STRC柱抗火性能进行系统深入分析．