基于自适应神经网络的异构多智能体系统一致性控制

李小萌, 刘心怡, 郑柏超

(南京信息工程大学自动化学院, 南京 210044)

近年来, 多智能体系统一致性问题广泛存在于无人机编队控制[1-2]和群集问题[3-4]等领域．多智能体一致性问题主要采用分布式控制协议, 其优点在于当某一个智能体出现故障时, 其余智能体可以在不影响整个系统运行的情况下继续完成任务, 同时各智能体间通过通信网络互相传递数据和共享信息, 最终完成整个控制系统的任务．

线性多智能体系统的结构简单, 其稳定性和鲁棒性易于分析, 这使得系统能实现精确控制, 但由于系统对外部条件的要求较高, 且绝大多数的实际工程问题都是非线性的或线性与非线性相结合的各类复杂问题, 故针对带有非线性的复杂多智能体系统控制方法的研究备受关注．Wang等[5]研究了有向相互作用拓扑下具有局部Lipschitz连续动力学的非线性多智能体系统编队问题, 基于满足局部Lipschitz连续条件的非线性动力学提出了3种滑模控制器来解决多智能体系统群体控制问题; Liu等[6]研究了具有Lipschitz非线性和未知扰动的奇异多智能体系统的一致性跟踪问题, 提出一种分布式控制协议, 在有向网络下分别得到了线性和Lipschitz非线性奇异多智能体系统一致性跟踪的充分条件．然而, 上述关于非线性系统的一致性控制结果都是基于非线性函数满足Lipschitz条件等性质已知的情况．对于给定系统, 通常难以获得未知非线性函数的性质[7]．径向基函数(radial basis function,RBF)神经网络可以在非线性函数性质未知的情况下有效地逼近非线性函数, 故可用于估计多智能体系统的非线性项[8]．Wen等[9]利用RBF神经网络逼近二阶多智能体系统中的非线性项, 通过选取较多的神经元数量和调节自适应参数获得理想的网络逼近精度; Zhang等[10]针对二阶非线性多智能体系统, 提出了基于RBF神经网络的一致性控制协议, 该方法避免了控制器的奇异性问题; Sharafian等[11]提出了一种基于RBF神经网络的滑模控制方法解决非线性多智能体系统的一致性问题, 利用RBF神经网络区分领导者和跟随者的不确定性, 并克服未建模的领导-跟随者的动力学问题．上述文献都是以二阶系统为主要研究对象, 而混合阶多智能体系统更符合实际的工程问题, 如一阶无人车与二阶无人机的组合等; 因此, 本文拟讨论含未知非线性的一阶/二阶异构多智能体系统的一致性问题, 并采用RBF神经网络对其二阶系统中的未知非线性项进行逼近处理, 再利用Lyapunov稳定性理论验证算法的有效性．

1 预备知识

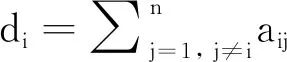
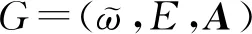
本文中λmin(D),λmax(D)分别为矩阵D的最小特征值和最大特征值; ‖·‖表示向量的2范数; ‖·‖F表示矩阵的F-范数．

2 问题描述

考虑由n个一阶线性智能体系统和m个二阶非线性智能体系统组成的异构多智能体系统．一阶线性多智能体系统

(1)

其中xi∈R,ui∈R分别为第i个智能体的位置状态和控制输入．二阶非线性多智能体系统

(2)

其中vi∈R为第i个智能体的速度状态,f(xi,vi)为未知非线性项．

假设1异构多智能体系统(1)(2)的通信拓扑图是无向连通图．

定义1[13]对于任意的初始位置xi(0)和初始速度vi(0), 若异构多智能体系统(1)(2)满足下列条件:

limt→∞‖xi(t)-xj(t)‖=0,i=1,2,…,n;

(3)

limt→∞‖vi(t)‖=0,i=n+1,n+2,…,n+m,

(4)

则系统(1)(2)可实现一致性．

3 RBF神经网络

对于任意光滑函数φ(z)∈R, 存在一个理想权值W*, 使得φ(z)=W*S(z)+ε(z), 其中S(z)=[s1(z),s2(z),…,sp(z)]T,ε(z)∈R为近似误差, 且满足条件‖ε(z)‖≤δ,δ为正常数．定义最优权值矩阵[14]为

4 控制协议设计

采用RBF神经网络对二阶多智能体系统(2)中的非线性函数f(xi,vi)进行近似估计,即

(5)

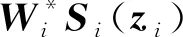
定义第i个智能体的位置一致性误差

(6)

其中aij为邻接矩阵A中第i行第j列中的通信系数．

基于神经网络近似式(5), 对异构多智能体系统(1)(2)设计自适应一致控制协议

(7)

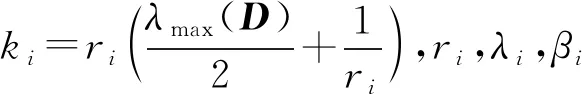
构造自适应律

(8)

其中γi,σi为正常数．

定理1对于异构多智能体系统(1)(2), 在一致性控制协议(7)和自适应律(8)的共同作用下, RBF神经网络可以逼近二阶多智能体系统(2)中的非线性项f(xi,vi), 同时异构多智能体系统能实现自适应一致．

证明 构造Lyapunov函数

(9)

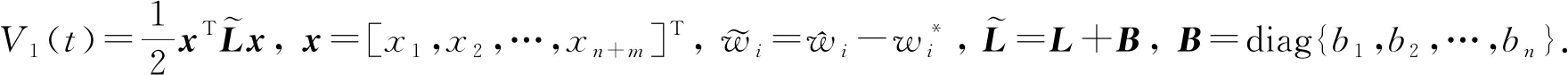
(10)

(11)

(12)

(13)

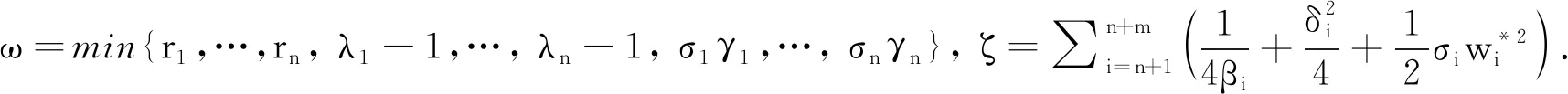
5 仿真分析

在MATLAB/Simulink环境下仿真验证本文所提异构多智能体系统的分布式自适应控制方法的有效性．选取4个智能体构建异构多智能体系统, 其中无人车1,2表示一阶线性智能体, 无人机3,4表示二阶非线性智能体, 智能体之间的通信拓扑结构如图1所示．

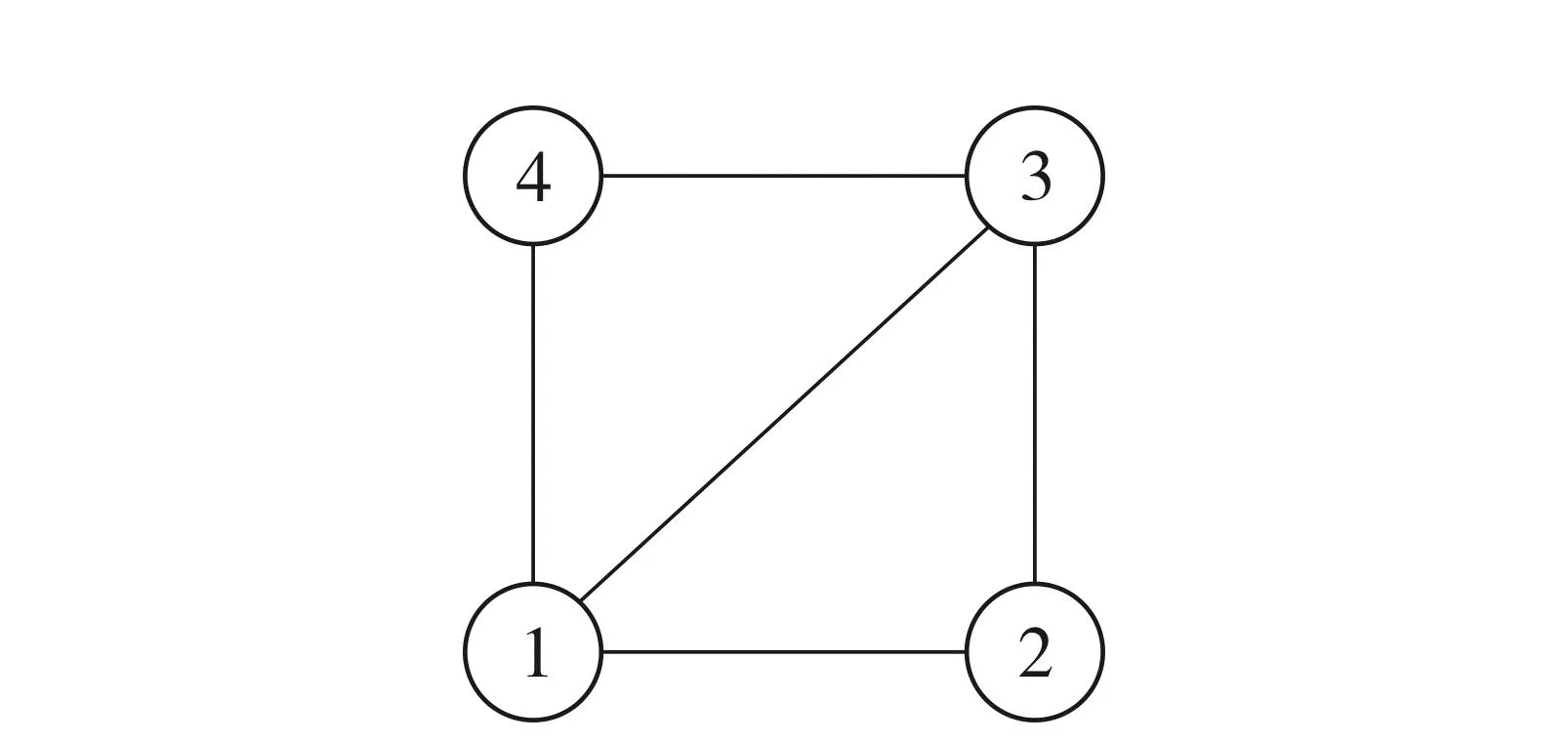
图1 系统的通信拓扑示意图Fig.1 Communication topology of the system

根据拉普拉斯矩阵可计算出最大特征值λmax(D)=2.561 6．RBF神经网络包含以μi为中心的36个节点, 全部节点在[1,1]×[1,1]范围内均匀间隔分配, 设置高斯函数的宽度bi=2．

二阶系统中的非线性项及其估计值如图2所示．由图2可见: 在本文控制协议的作用下, RBF神经网络能够逼近二阶系统中的非线性项．

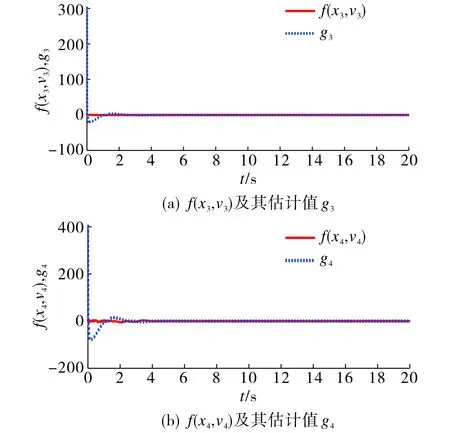
图2 系统的非线性项及其估计值Fig.2 The nonlinear term of the system and its estimated value

4个智能体的控制输入和一致性误差如图3所示．由图3可见: 误差变量可迅速收敛至0, 表明该控制协议是有效的．

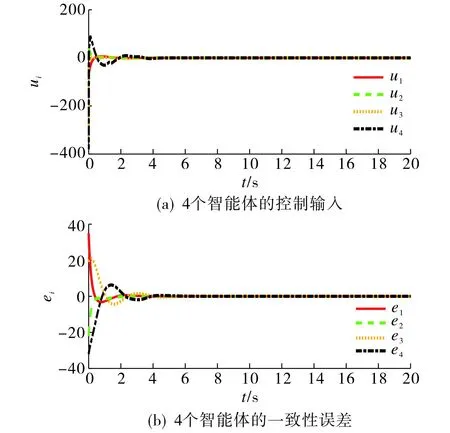
图3 系统的控制输入和一致性误差Fig.3 Control input and consistency error of the system

为了验证本文设计的RBF神经网络分布式控制协议的优越性, 现与传统的分布式控制协议[15]进行对比, 2种控制协议作用下系统状态达到稳定所需时间如表1所示, 系统中4个智能体的位置状态响应曲线和2个二阶智能体的速度状态响应曲线分别如图4～5所示．由表1可知: 相对于传统的分布式控制协议, 本文提出的自适应分布式控制方法在位置稳定时间和速度稳定时间上分别提升了2%和11%．由图4～5可知: 系统状态在本文设计的分布式控制协议下能快速收敛并实现一致性, 进一步验证了本文方法的有效性和优越性．

表1 不同控制协议下系统状态达到稳定所需时间

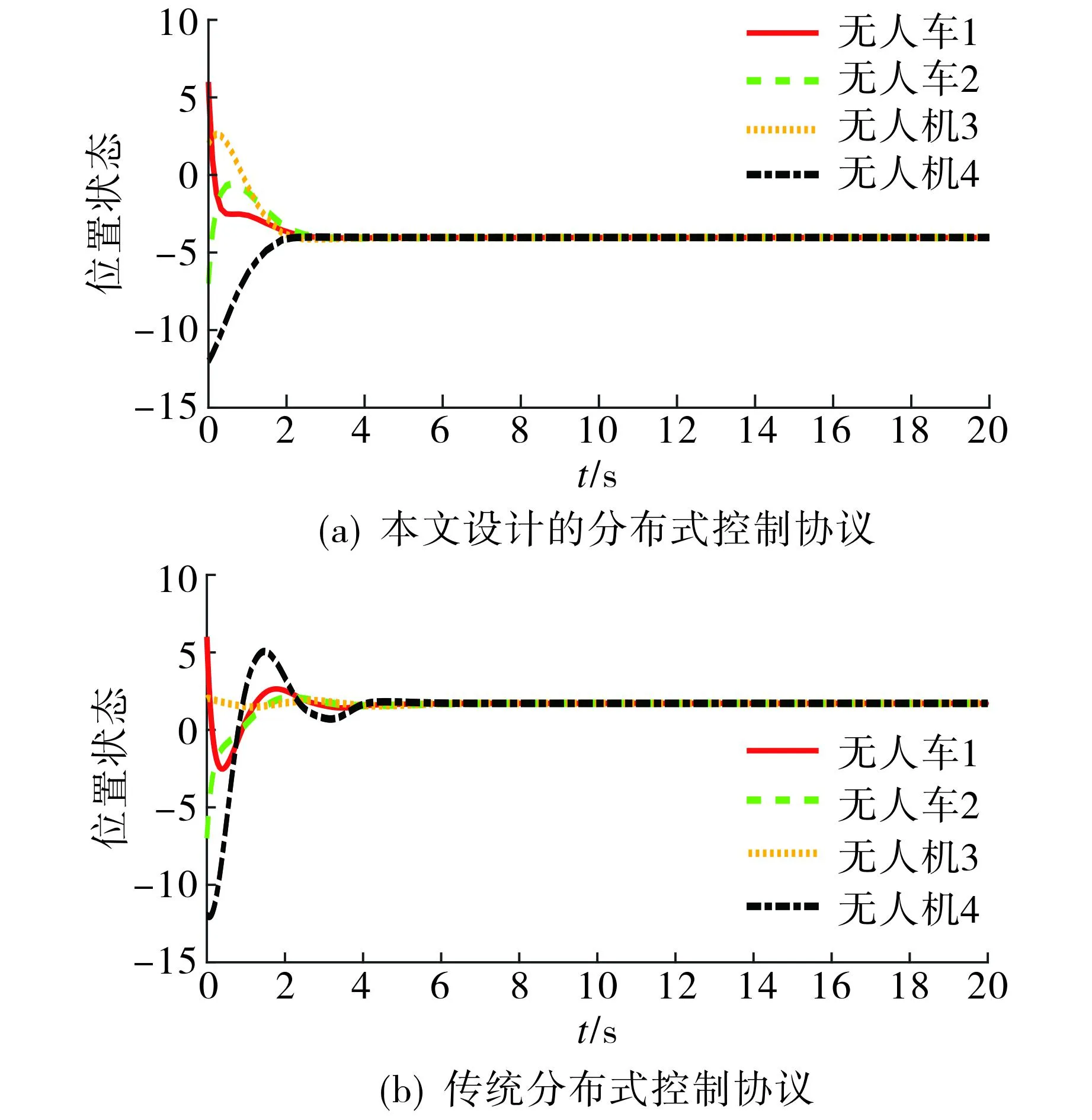
图4 系统位置状态响应曲线Fig.4 System position state response curves

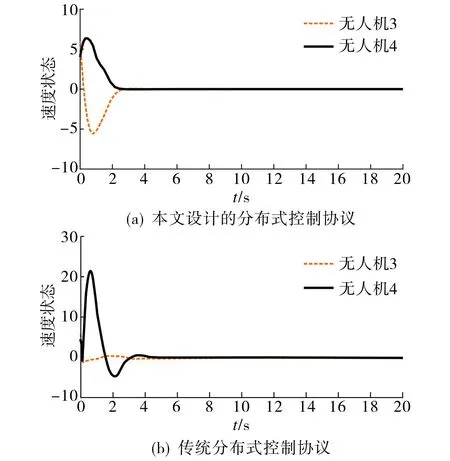
图5 系统速度状态响应曲线Fig.5 System velocity state response curve

6 结语

本文研究了由一阶线性智能体和二阶非线性智能体组成的异构多智能体系统, 针对二阶多智能体系统中的未知非线性项, 设计了一种利用RBF神经网络有效逼近未知非线性的自适应分布式控制协议．与现有的一致性方法相比, 自适应神经网络方法的在线计算量有所下降．通过Lyapunov稳定性理论证明了该自适应分布式控制协议能实现一阶/二阶异构多智能体系统的自适应一致性目标．MATLAB/Simulink仿真结果验证了该分布式控制协议的有效性．