直接互惠下量子囚徒困境的演化稳定分析

付子芮， 王新颖， 程 程， 张新立

（辽宁师范大学 数学学院，辽宁 大连 116029）

无论是自然界还是人类社会，合作现象都是普遍存在的，演化博弈理论为合作行为的研究提供了有效的理论框架。囚徒困境是博弈论中广泛使用的范例，很多学者利用该模型讨论合作演化的稳定性问题，其中以直接互惠来研究合作行为的演化稳定性最为常见。直接互惠的博弈论框架是迭代囚徒困境，Pacheco等[1]研究了动态结构种群中直接互惠下合作的演化，推导出演化稳定性的条件。Hilbe 等[2]以迭代囚徒困境为主要模型，讨论得出当种群数量大且关系稳定时，直接互惠促进合作的演变。Ohtsuki等[3]拓展了囚徒困境的标准框架，让参与人在合作、背叛和惩罚中做出选择，得出在直接互惠的背景下自然选择更倾向于合作。

上述文献虽然已经从完全理性发展到了有限理性分析框架，但在刻画参与人支付函数方面还是没有突破经典博弈论所建立的期望效用理论范式。直接互惠可能在这种理论前提假设下使个体之间形成一个合作演化均衡，但却很难解决合作系统内个体间争夺公共资源、为公共资源的有限性而发生冲突从而导致合作系统解体等问题。Eisert等[4]提出了量子策略的概念，构建了一个特定的量子策略去解决经典博弈构成的困境。孙庆文等[5]基于不完全信息假设，对演化博弈均衡进行稳定性分析，并给出定性行为的拓扑等价分类。Du等[6]将量子囚徒困境推广到玩家共享非最大纠缠态的情况，利用NMR实现了囚徒困境模型量子策略。

综上，运用量子纠缠分析参与者的理性程度可为理性的定量研究提供新思路，也对博弈结果产生影响。对于经典囚徒困境模型，使用EWL量子化方案可以改变经典策略所产生的困境，使用合作机制可以促进参与者选择合作。目前很多国内外学者将5种合作机制单独或者多种机制共同引入囚徒困境模型中，而在量子策略中，目前鲜少有学者进行量子囚徒困境模型在合作机制作用下的演化博弈分析的研究。因此，本文将直接互惠引入量子囚徒困境中，建立了直接互惠下的量子囚徒困境模型，并进行演化博弈分析，讨论出在这种策略下演化稳定性的条件。此理论不仅拓展了传统博弈模型支付函数的表达形式，而且可在直接互惠和纠缠统一框架下解决人类社会普遍存在的竞争和冲突等问题，具有重要的现实指导意义。

1 模型假设与构建

1.1 量子博弈模型的假设与建立

囚徒困境中，个体有合作(C)和背叛(D)两种选择。当C与C相遇时，C获得的收益是3；当C与D相遇时，C获得的收益是0，D 获得的收益是5；当D 与D 相遇时，D获得的收益是1，收益矩阵如表1所示。

由表1可知，（背叛，背叛）是唯一的纳什均衡。当双方均选择合作时集体收益最大，但每个参与人都从背叛中获得更高的个人利益，反映出个人理性与集体理性的矛盾。为解决这一困境，Li 等[7]提出了量子囚徒困境博弈，引入量子纠缠度γ到经典的囚徒困境中，得到了量子囚徒困境的收益矩阵。王龙等[8]论述了量子博弈的研究现状和最新进展，介绍了Eisert量子博弈模型。令2个主体的策略都是,即该博弈的状态为，通过量子门̂使得状态纠缠在一起形成初始状态，即2个主体的初始状态形成纠缠状态。2个主体A和B的策略分别为酉算子和，当进行一次博弈后，通过量子门Ĵ来解纠缠，得到最终状态。使用囚徒困境收益矩阵(表1)，定义A的收益矩阵为：$A= 3∗PCC+ 1∗PDD+ 5∗PDC+ 0∗PCD。在这种情况下，存在一个量子策略使得均衡(Q,Q)是一个新的Nash均衡，并且是一个Pareto最优，因此困境在量子策略下消失了。纠缠程度也是影响量子博弈的一个重要因素，本文用新的Nash 均衡策略Q替换经典合作策略C，得到了量子囚徒困境博弈的收益矩阵。

从表2 可以看出，当γ= 0 时，量子博弈将回到经典博弈，经典囚徒困境模型是量子囚徒困境模型的一种特殊形式；当γ=时，量子策略Q 是唯一的Nash均衡，并且是Pareto最优解；当)时，随着γ的增大，（背叛，合作）和（合作，背叛）的收益趋向于（合作，合作）的收益，（合作，合作）策略组合越来越稳定。因此，量子囚徒困境模型是经典囚徒困境模型的推广。

表2 量子囚徒困境的收益矩阵Table 2 Payoff matrix of quantum prisoner′s dilemma

1.2 直接互惠下量子囚徒困境模型的建立

直接互惠被认为是一个强大的合作机制，许多学者研究了直接互惠在迭代博弈中促进合作的演化。Nowak[9]通过研究“总是合作”和“总是背叛”的相互作用，推导出合作在迭代囚徒困境演化中的必要条件，得出囚徒困境在直接互惠下的收益矩阵。Rand等[10]基于迭代囚徒困境模型构建了直接互惠下的合作者和背叛者的收益矩阵。直接互惠基于“你帮助我”和“我帮助你”的概念，在每一轮博弈中，两名参与人必须选择合作或背叛。设ω为下一轮相遇的可能性，其中ω∈(0,1)，每一轮的平均数为，由此得到了直接互惠下的量子囚徒困境收益矩阵（表3）。

表3 直接互惠下的量子囚徒困境收益矩阵Table 3 Quantum Prisoner′s Dilemma payoff Matrix under direct reciprocity

2 两策略的演化稳定性分析

在博弈过程中，博弈方1和博弈方2选择合作的概率分别为x、y，选择背叛的概率分别为1 -x、1 -y，其中x∈[0,1],y∈[0,1]。博弈方1采取“Q策略”和“D策略”的期望收益和二者平均收益分别为：

由于博弈是对称的，博弈方2采取“Q策略”和“D策略”的期望收益和二者平均收益计算过程与博弈方1相同，因此博弈方1、2采取合作策略的复制子动态方程分别为

2.1 平衡点的局部稳定性分析

根据演化稳定策略的性质与微分方程的稳定性定理：若一个策略(x,y)是演化稳定策略，需要满足

2.1.1 （合作，合作）是演化稳定策略

2.1.2 （背叛，背叛）是演化稳定策略

2.1.3 （合作，背叛）和（背叛，合作）为演化稳定策略

2.2 直接互惠参数和量子纠缠对均衡点的影响分析

量子纳什均衡点D的局部稳定性与ω、γ密切相关，其中x0=y0=，在其余参数不变的情况下，仅改变ω、γ的数值会使局部稳定区域发生变化。由于x0、y0相同，下面利用多元函数微分学讨论参数ω、γ对x0的影响。

2.2.1ω对x0的影响

在参数γ不变的情况下，<0，x0为关于ω的减函数；当< sin2γ< 1,>0，x0为关于ω的增函数。综上可知当0 < sin2γ<时，合作行为与直接互惠呈负相关，直接互惠行为抑制合作；当< sin2γ< 1时，合作行为与直接互惠呈正相关，即直接互惠行为促进合作。

2.2.2γ对x0的影响

在参数ω不变的情况下因此当<ω< 1时，合作行为与纠缠呈正相关，纠缠促进合作的演化；当0 <ω<时，合作行为与纠缠呈负相关，即纠缠抑制合作的演化。

2.3 模拟数值仿真与分析

现在研究O、A、B、C、D均衡点演化策略的渐近稳定性。为进一步验证量子纠缠和直接互惠促进合作演化的问题，使结果更具直观性，本文利用Matlab对均衡点进行模拟仿真分析，结果如图1和图2所示。

图1 量子纠缠下ω对均衡点x0的影响Figure 1 The influence of ω on equilbrium point(x0) under quantum entanglement

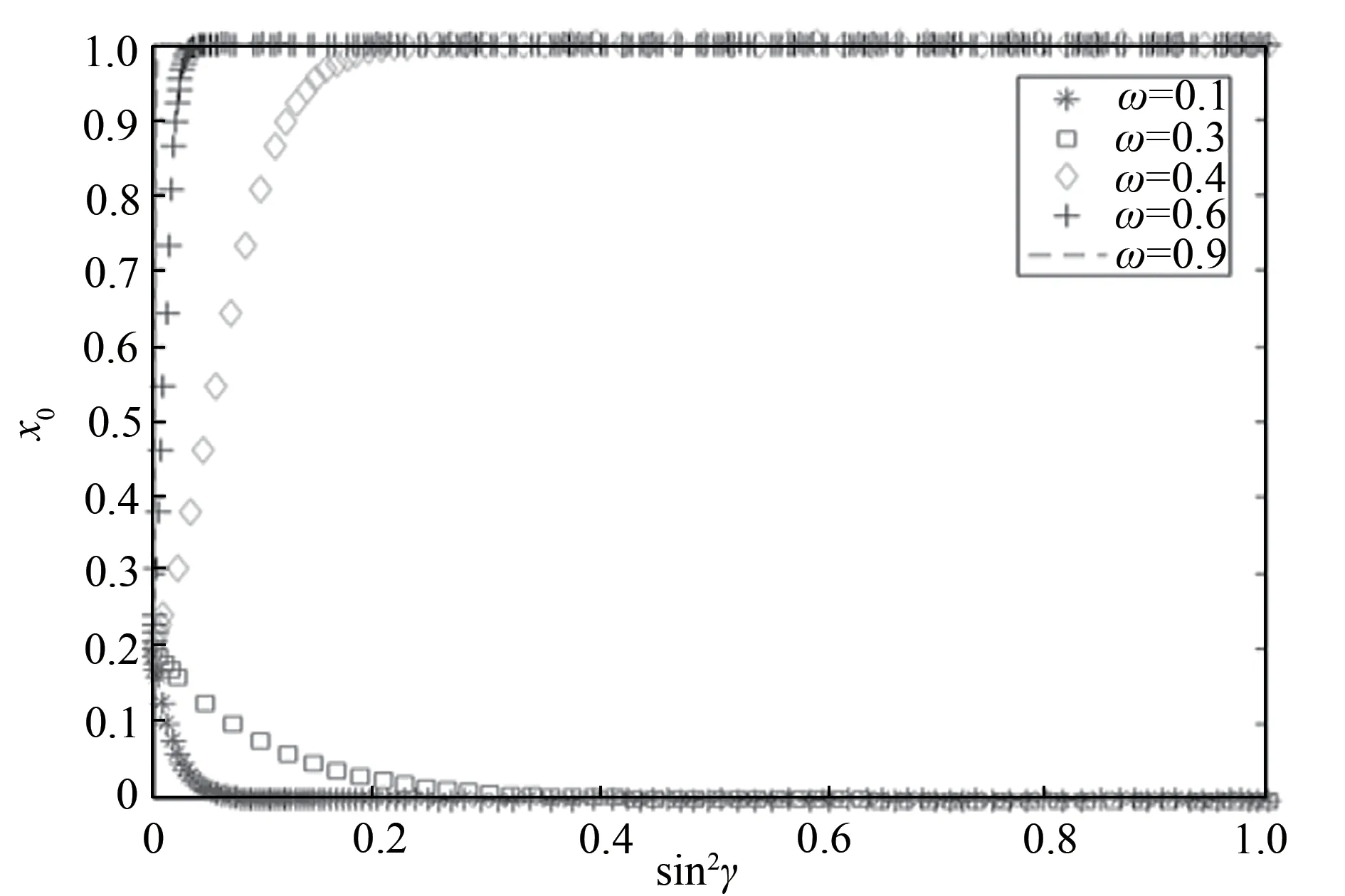
图2 直接互惠下sin2γ对均衡点x0的影响Figure 2 The influence of sin2γ on equilbrium point(x0)under direct reciprocity

从图1可知，当sin2γ> 0.2时，合作行为与直接互惠呈正相关，即直接互惠行为促进合作；sin2γ< 0.2时，合作行为与直接互惠呈负相关，即直接互惠行为抑制合作，且纠缠γ越大，演化速度越快。从图2可以看出，当ω>时，纠缠促进合作；当ω<时，纠缠抑制合作。数值仿真与本文理论内容符合。

3 结论

本文基于演化博弈理论建立直接互惠下量子囚徒困境模型，通过求解均衡点和对均衡点的稳定性分析，讨论合作策略和背叛策略为演化稳定策略的条件以及直接互惠参数和纠缠对均衡点的影响，得出结论：当直接互惠参数ω不变时，sin2γ> 0.2，直接互惠行为促进合作；当纠缠γ不变时，ω>，纠缠促进合作的演化。量子策略给博弈论提供了新的视角和思路，量子演化稳定策略的分析也为博弈均衡提供了新的途径。