模型意识在求解三角形最值(范围)问题中的应用

林厚栋

(福清融城中学,福建 福州 350300)

解三角形中的最值(范围)问题往往与平面解析几何、三角函数、导数、基本不等式等相关知识加以交汇与融合,充分体现了新课标中“在知识的交汇处命题”的指导思想.此类问题较全面地考查学生的识别模型的能力、化归与转化能力以及运算求解能力等.破解此类问题的关键是要基于问题情境,依托图形特征或目标问题导向,树立模型意识,并以模型为导向,结合正余弦定理实施合理转化,进而构建出具体的模型实现问题的求解.

1 策略剖析

解三角形本质上是在三角形内蕴方程(三角形的正弦定理、余弦定理、三角形内角和定理以及三角形两边之和大于第三边)的基础上,把试题设定的条件(方程)与内蕴方程建立起联系,从而得到三角形的全部或者部分度量关系.而度量关系的形成,就需要对已知条件进行深度加工或对图形中隐藏的内蕴特征进行挖掘,把情境问题模型化,以利于顺利求解问题.解三角形中有关的最值(范围)问题常见的解题路径是: 直观感知(直观数式和直观几何图形特征)、识别模式(建立已知和未知之间的联系)、引入变量(边或角)、建立模型、问题求解.

解三角形中的最值(范围)问题,最根本的落脚点是树立模型化思想,模型化思想的内涵包含函数模型的建立或者隐形的轨迹方程模型的确认,轨迹模型常有圆、椭圆、双曲线等.在运用动点的轨迹方程模型中,首先要通过观察发现三角形的边与边之间的数量关系,进而借助平面几何的相关知识以及图形的直观意识,利用数形结合思想,直观感知其轨迹方程中的图形特征,借助化归转化等思想快速地实现问题的求解.

2 应用赏析

(1)写出函数解析式S(x);

(2)求S(x)的最小值.

(2)由(1)知,

评注本题中以角为变量,利用正弦定理以及三角形的面积公式建立目标函数S(x)模型,通过三角恒等变换,求得函数S(x)的最值,并注意结合具体的图形特征限制变量的取值范围.

解法1设BC=x,则AC=2x,由面积公式得

①

根据余弦定理得

将其代入①式得

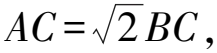
化简可得(x-3)2+y2=8.

故点C的轨迹是一个圆(x-3)2+y2=8(y≠0).

图1 解法2图

解析由题知,sinB=-cosC>0.

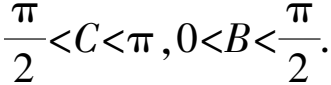
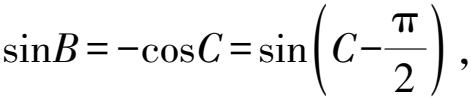
解析设CD=2BD=2x>0,在△ABD中,AB2=BD2+AD2-2BD·ADcos∠ADB=x2+4+2x,

同理AC2=4x2+4-4x,

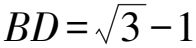
评注例3涉及的最值问题求解是基于构建以角为变量的函数模型,依托二倍角公式,并结合正弦定理的转化,巧妙而简明地利用基本不等式来确定对应的最值问题,回归解三角形本质,使问题的求解变得自然顺畅.例4问题中呈现的三角形给出了一条边上一个三等分点到顶点的长度和一个特殊角,但这些条件是无法确定原三角形的大小和形状的.因此就要求在理解三角形变化的过程中,依托已知条件CD=2BD,并结合问题目标,选取边BD作为基本变量,以两个三角形为载体,运用余弦定理,把问题转化成函数的最值问题.

正如波利亚在《怎样解题》中所提到的:没有任何一道题是彻底完成了的,总会有些事情可以做[1].只有将立足模型与立意思想两者交相融合,才能使问题的解决和素养的发展齐头并进,才能将数学问题解答得更加“挥洒自如、甄于完美”,使学生对数学问题的本质理解得更加透彻,对问题中所蕴含的数学思想领悟得更加深刻,学生的思维品质亦能得到更好的发展,基础知识得以进一步夯实,关键能力从中也得到显著提高,最终促使学生数学核心素养真正落地.