一道与线段比有关的向量问题解法探索
2024-01-10唐宜钟
唐宜钟
(汉中市龙岗学校,陕西 汉中 723100)
向量兼具代数和几何的双重特性,同时有着现实的物理意义.因此,在遇到有关问题时,我们可以从代数、几何和物理模型三个方面进行解答.而不同的解答方式,会从不同角度去阐释问题,并分析其之间的内在联系性[1].
1 解法探索


图1 题目图











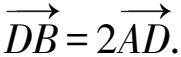

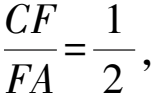






图2 建系法
从而(m-xD,n-yD)=2(xD-3,yD).












图3 平行线法
过点F作FK∥AE,交BC于点K,则



图4 面积法
不妨设SA=2,则SB=1,SC=4.




图5 梅涅劳斯定理





杠杆原理杠杆原理亦称杠杆平衡条件, 即要使杠杆平衡, 作用在杠杆上的两个力矩 (力与力臂的乘积) 大小必须相等,即:动力×动力臂=阻力×阻力臂 (F1·L1=F2·L2).具体解释如下:对于线段AB,将其视为轻质杠杆,O为支点.如果在AB的端点处分别放置质量为m1,m2的两个质点,使杠杆平衡,则有m1·AO=m2·BO,或AO∶BO=m2∶m1.此时,支点O处所承受的质量为mO=m1+m2.



图6 杠杆法
由杠杆法,各支点质量为
mD=mA+mB=3,mE=mB+mC=5,mF=mC+mA=6.





2 解法关联

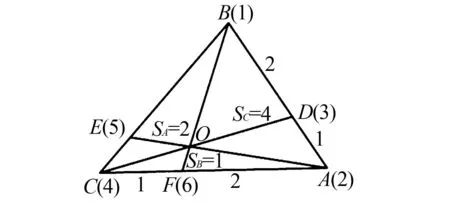
图7 两种解法关联

图8 各种解法关联
3 变式训练

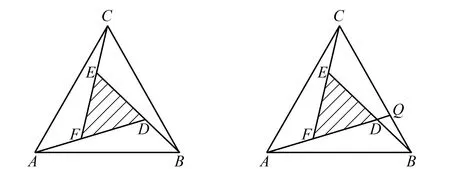
图9 变式1示意图图10 变式1解析图
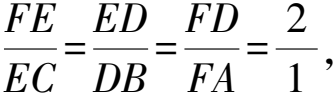
进而mB=6,mD=mE+mB=9.
如图10,延长FD交BC于点Q,则
mQ=mD-mF=8.












解法2(解三角法)设BD=x,AD=y,则CD=2x.
在△ABC中,由余弦定理,有
9x2=b2+c2-bc.
①
在△ABD和△ACD中,由余弦定理,有
又∠ADB+∠ADC=π,
所以cos∠ADB=-cos∠ADC.

整理,得6x2+3y2=2c2+b2.
②
由①②,得9y2=b2+4c2+2bc.



图11 变式2建系法





图12 变式2平面几何法





解法5(解析法) 以BC为x轴,BC中垂线为y轴,建立坐标系,不妨设BC=6.则B(-3,0),C(3,0),则D(-1,0).

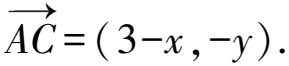


4 几点感悟
4.1 注重一题多解、多解归一和优解选择
一题多解和多解归一缘于数学的多元表征性.所谓表征,是指可反复指代某一事物的任何符号或符号集.通常把事物的不同表征形式叫做该事物的多元表征.如果问题信息可以转化为多种表征方式,且不同表征之间存在着实质性的联系,那么我们就可以多角度地分析理解问题,从而达到一题多解和多解归一.在本文中,向量可以从代数、平面几何、解析几何、物理意义等多个角度进行切入,切入后通过转化,发现其本质的同一性,进而可以实现思维角度的多解归一.当然,不同的解法书写表达、思维难度、运算复杂度各不相同,在具体做题过程中,要做到合理选择.如本文所述问题出现在选择填空题中,杠杆法无疑是最快捷的方法[3].
4.2 在解题中逐渐提升知识关联的认知
郑毓信先生提倡教学时,不是求全,重要的是求“联”,这里的“联”就是联系、关联.认知关联包括知识关联、研究路径关联、研究方法关联.在解题过程中,教师需着眼认知关联教学,将研究内容与已有认知经验关联,引导学生在发现与建立关联中规划研究路径“延伸线”,在揭示与确认关联中激活研究方法“衔接点”,在内化与完善关联中形成数学知识“生长链”,从而提升学生的思维品质,发展学生的思维能力.在本文中,从基底法出发,到向量的参数方程法,实现了解题路径的延伸.而面积法、定理法、杠杆法、奔驰定理法既实现了向量代数和几何性质的衔接,又完成了知识的生长[4].
4.3 适当积累高位知识
所谓高位知识,是指在学生知识体系之外,高于学生认知的知识,其包括高等数学的弱化、初等数学的升华、跨学科的融合等.高位知识并非深不可测,它只需学生在现有知识体系内,往前迈出一小步.如本文中的梅涅劳斯定理和塞瓦定理,只需要初中平面几何知识就可理解.适当地积累高位知识,就能站在更高角度寻找路径,贯穿各种“形似”“神似”的想法,发现某些数学必然的本质.如站在“面积法”的角度,就可以展望到本文中杠杆法和奔驰定理法,也可延伸到(梅涅劳斯、塞瓦)定理法,而定理法又可解释平行线法和面积法.
