再谈抽象函数对称问题的求解与拓展

侯有岐

(陕西省汉中市四○五学校,陕西 汉中 723312)

抽象函数是指没有给出具体的函数解析式或图象,只给出一些函数符号及其满足条件的函数,如函数的定义域、解析递推式、特定点的函数值、特定的运算性质等.它是高中函数部分的难点,也是大学高等数学函数部分的一个衔接点.

下面笔者以2022年高考数学全国卷中的三道抽象函数为例,先探究试题背景,然后对相关试题进行对比研究,整理出抽象函数对称性、奇偶性、周期性问题的一般化性质,以期抛砖引玉.

1 试题呈现

C.f(-1)=f(4) D.g(-1)=g(2)

A. -21 B. -22 C. -23 D.-24

A. -3 B. -2 C. 0 D.1

这三道试题都是涉及抽象函数及其导函数之间的对称性(轴对称、中心对称)和周期性的综合题.这类问题主要考查学生数学语言的转化能力、推理运算能力以及抽象思维能力.解决这类问题的关键就是要把隐蔽在抽象函数中的对称性和周期性挖掘出来并应用于解题过程中[1].

下面我们先来研究有关抽象函数的一般性质,为解决相关问题探寻更有效的策略.

2 性质探究

2.1 抽象函数对称性的几个重要结论

事实上,根据函数图象的概念及对称图形的定义,不难证明以下结论.

推论1 若函数y=f(x)定义域为R,且满足条件:f(a+x)=f(a-x),则函数y=f(x)的图象关于直线x=a对称.

推论2 若函数y=f(x)定义域为R,且满足条件:f(x)=f(2a-x)),则函数y=f(x)的图象关于直线x=a对称.

可以看出,函数f(x)满足的条件中x的系数一个为1,另一个为-1,相应解析式的自变量相加除以2,可得y=f(x)图象的对称轴方程.

推论3 若函数y=f(x)定义域为R,且满足条件:f(a+x)=f(a-x), 又若方程f(x)=0有n个根,则此n个根的和为na.

推论2若函数y=f(x)定义域为R,且满足条件:f(a+x)+f(a-x)=0(a为常数),则函数y=f(x)的图象关于点(a,0)对称.

可以看出,上面的f(x)满足的条件中x的系数一个为1,另一个为-1时,函数f(x)图象存在对称中心.

推论1 函数y=f(x-a)与函数y=f(a-x)的图象关于直线x=a对称.

推论2 函数y=f(a+x)与函数y=f(a-x)的图象关于直线x=0对称.

上述常用结论中四个性质的本质完全不同.性质1是探讨一个函数的图象本身关于某条直线的对称问题,即自身轴对称问题;性质2是探讨一个函数的图象本身关于某点的对称问题,即自身中心对称问题;性质3是探讨两个函数的图象关于某条直线的对称问题,即相互轴对称问题;性质4是探讨两个函数的图象关于某点的对称问题,即相互中心对称问题.解题时要注意它们的区别.

进一步拓展问题,不难证明上述四个性质的更一般形式:

2.2 抽象函数周期性的几个重要结论

在以下各式中,x取其定义域内的任意值,且a,b,T为非零常数,a≠b,则不难证明如下结论:

性质9若f(x±T)=f(x),则y=f(x)的周期为T,kT(k∈Z,k≠0)也是函数的周期.

性质10若f(x+a)=f(x+b),则y=f(x)的周期为|b-a|.

性质11若f(x+a)=-f(x),则y=f(x)的周期为2|a|.

推论4若f(x+a)+f(x)=c,则y=f(x)的周期为2|a|.

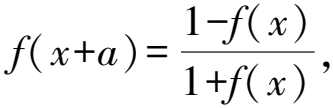
性质15若f(x+2a)=f(x+a)-f(x),则y=f(x)的周期为6|a|.

2.3 抽象函数的周期性与双对称性间的关系

类比正弦函数y=sinx和余弦函数y=cosx的图象及周期,可以猜想并证明如下结论:

性质16 (两线对称型)设f(x)是定义在R上的函数,其图象关于直线x=a和x=b(b>a)对称,则函数y=f(x)的周期为2(b-a).

性质17 (两点对称型)设f(x)是定义在R上的函数,其图象关于点(a,0)和点(b,0)(b>a)对称,则函数y=f(x)的周期为2(b-a).

性质18(一线一点对称型)设f(x)是定义在R上的函数,其图象关于直线x=a和点(b,0)(b>a)对称,则函数y=f(x)的周期为4(b-a).

2.4 抽象函数与导函数之间的对称性和周期性

性质19已知函数f(x)及其导函数f′(x)的定义域为R.

(1)若f(x)关于直线x=a对称,则f′(x)关于点(a,0)对称.

(2)若f(x)关于点(a,t)对称,则f′(x)关于直线x=a对称．

证明(1)若f(x)关于直线x=a对称,则f(a+x)=f(a-x).求导得f′(a+x)=-f′(a-x).

所以f′(x)关于点(a,0)对称．

(2)若f(x)关于点(a,t)对称,则f(a+x)+f(a-x)=2t.求导得f′(a+x)=f′(a-x).

即f′(x)关于直线x=a对称.

在性质1中,当a=0,t=0时,有如下结论:

推论已知函数f(x)及其导函数f′(x)的定义域为R．

(1)若f(x)关于直线x=0即y轴对称,则导函数f′(x)关于原点(0,0)对称.

也就是:若f(x)是偶函数,则其导函数f′(x)是奇函数.

(2)若f(x)关于原点(0,0)对称,则导函数f′(x)关于直线x=0即y轴对称.

也就是:若f(x)是奇函数,则其导函数f′(x)是偶函数.

性质20已知函数f(x)及其导函数f′(x)的定义域为R.若导函数f′(x)关于直线x=a对称,则函数f(x)关于点(a,t)对称.

证明若f′(x)关于直线x=a对称,则f′(a+x)=f′(a-x).有f(a+x)+f(a-x)=2t.

即函数f(x)关于点(a,t)对称.

注意若f′(x)关于点(a,t)对称,则f(a+x)+f(a-x)=2t,得f(a+x)-f(a-x)=2m,并非f(a+x)=f(a-x),即函数f(x)不一定关于直线x=a对称.

性质21已知函数f(x)及其导函数f′(x)的定义域为R.若函数f(x)是周期为T的函数,则其导函数f′(x)也是周期为T的函数.

证明若函数f(x)是周期为T的函数,则f(x+T)=f(x),求导得f′(x+T)=f′(x).即导函数f′(x)也是周期为T的函数.

注意若导函数f′(x)是周期为T的函数,则f′(x+T)=f′(x),得f(x+T)=f(x)+m.故函数f(x)不一定是周期为T的函数.

例如,函数f(x)=sinx+x,f′(x)=cosx+1,导函数f′(x)是周期函数,但f(x)不是周期函数.

2.5 复合函数的奇偶性

定义1若对于定义域内的任一变量x,均有f[g(-x)]=f[g(x)],则复数函数y=f[g(x)]为偶函数.

定义2若对于定义域内的任一变量x,均有f[g(-x)]=-f[g(x)],则复合函数y=f[g(x)]为奇函数.

说明(1)复合函数y=f[g(x)]为偶函数,则f[g(-x)]=f[g(x)],而不是f[-g(x)]=f[g(x)];复合函数y=f[g(x)]为奇函数,则f[g(-x)]=-f[g(x)],而不是f[-g(x)]=-f[g(x)].

(2)两个特例:若y=f(x+a)为偶函数,则f(x+a)=f(-x+a);若y=f(x+a)为奇函数,则f(-x+a)=-f(x+a).

(3)y=f(x+a)为偶(或奇)函数,等价于单层的函数y=f(x)的图象关于直线x=a轴对称(或关于点(a,0)中心对称).

3 试题解答

根据上述结论,不难得到上述三道试题的具体解答过程如下:

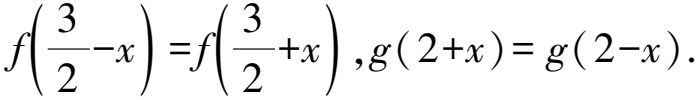
所以f(3-x)=f(x),g(4-x)=g(x).

则f(-1)=f(4),故C正确.

所以g(4-x)=g(x)=-g(3-x).

所以g(x+2)=-g(x+1)=g(x).

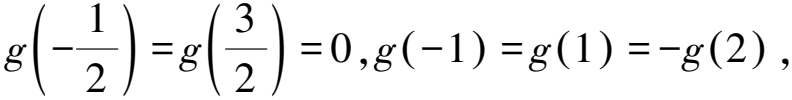
若函数f(x)满足题设条件,则函数f(x)+C(C为常数)也满足题设条件,所以无法确定f(x)的函数值,故A错误.故选BC.

点评解决本题的关键是转化题干条件为抽象函数的性质,准确把握原函数与导函数图象间的关系,准确把握函数的性质(必要时结合图象)即可得解.

题2解析因为y=g(x)的图象关于直线x=2对称,所以g(2-x)=g(x+2).

因为g(x)-f(x-4)=7,

所以g(x+2)-f(x-2)=7.

即g(x+2)=7+f(x-2).

因为f(x)+g(2-x)=5,所以f(x)+g(x+2)=5.

代入得f(x)+[7+f(x-2)]=5.

即f(x)+f(x-2)=-2.

所以f(3)+f(5)+…+f(21)=(-2)×5=-10,

f(4)+f(6)+…+f(22)=(-2)×5=-10.

因为f(x)+g(2-x)=5,所以f(0)+g(2)=5,即f(0)=1,所以f(2)=-2-f(0)=-3.

因为g(x)-f(x-4)=7,所以g(x+4)-f(x)=7.

又因为f(x)+g(2-x)=5,联立,得

g(2-x)+g(x+4)=12.

所以y=g(x)的图象关于点(3,6)中心对称.因为函数g(x)的定义域为R,所以g(3)=6,因为f(x)+g(x+2)=5,所以f(1)=5-g(3)=-1.

点评含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当转化,然后得到所需的一些数值或关系式从而解题.

题3解析因为f(x+y)+f(x-y)=f(x)f(y),令x=1,y=0可得,2f(1)=f(1)f(0),所以f(0)=2.

令x=0可得,f(y)+f(-y)=2f(y).

即f(y)=f(-y).

所以函数f(x)为偶函数.

令y=1,得f(x+1)+f(x-1)=f(x)f(1)=f(x).

即有f(x+2)+f(x)=f(x+1).

从而可知f(x+2)=-f(x-1),

f(x-1)=-f(x-4).

故f(x+2)=f(x-4).

即f(x)=f(x+6).

所以函数f(x)的一个周期为6．

因为f(2)=f(1)-f(0)=1-2=-1,f(3)=f(2)-f(1)=-1-1=-2,f(4)=f(-2)=f(2)=-1,f(5)=f(-1)=f(1)=1,f(6)=f(0)=2,所以一个周期内的f(1)+f(2)+…+f(6)=0．

点评首先对题目给出的抽象函数的性质进行理解,然后通过变量赋值,把抽象函数问题转化为具体的数学问题,从而问题得解,这是解决抽象函数问题常用的方法之一.

高考试题对高考复习教学具有很强的导向作用.本文通过对2022年高考数学全国卷中三道抽象函数问题的研究,对抽象函数的一般性质作了系统的归纳整理,从而使学生对本部分知识有了进一步的理解.只有研究高考试题的不同解法及其相关性质,并从中挖掘高考试题的导向功能,才能更好地把握复习备考的方向,提高复习斜率.