基于WOA优化Elman神经网络的露天矿边坡位移预测

2024-01-10戚鑫鑫杨逸飞高彩云

河南城建学院学报 2023年6期

高宁，戚鑫鑫，杨逸飞，高彩云

（1.河南城建学院测绘与城市空间信息学院，河南平顶山467036；2.安徽理工大学空间信息与测绘工程学院，安徽淮南 232001；3.高分辨率对地观测系统河南数据与应用中心平顶山分中心，河南平顶山 467036；4.白俄罗斯国立经济大学，白俄罗斯明斯克 220071）

露天开采是我国矿产资源开发的主要形式，在开采过程中形成了大量的矿边坡工程。随着开采深度、堆排高度和边坡角度不断增大，边坡稳定性变差，由此引发的露天矿安全风险日益突出，制约了区域经济和社会的可持续发展［1］。为降低露天矿安全风险，迫切需要建立准确的边坡变形预测模型，及时掌握边坡变形发展趋势，实现提前预测、预报和预警。

露天矿边坡始终处于复杂的动态开挖、回采过程，且影响因素复杂多变［2］，因此具有明显的“动态”特征。目前，学界关于边坡变形预测的方法主要有时间分析、小波分析、灰色系统理论、神经网络等［3］。其中，神经网络因其具有较强的非线性映射能力、自主学习能力优等特点，被广泛用于边坡工程变形预测。如林国平［4］采用BP神经网络对降雨条件下的边坡变形演化发展进行了较为准确的预测；欧阳斌等［5］利用优化后的BP神经网络对安家岭露天煤矿1270平盘边坡位移开展预测，预测结果与实测值较为吻合；刘利君等［6］应用RBF神经网络对白音华二号露天矿南帮边坡位移进行了预测；韩亮等［7］提出了基于RBF神经网络的露天矿边坡稳定系数预测模型。虽然BP、RBF神经网络能够用于露天矿边坡位移预测，但其建模原理都是将动态时序问题转变为适合算法本身的静态问题，而这与露天矿边坡工程数据的动态特性不匹配，会影响预测结果的合理性、正确性。

基于此，本文引入具有动态反馈功能的Elman神经网络，并通过鲸鱼算法（Whale Optimization Algorithm，WOA）获取最佳权值和阈值，构建露天矿边坡WOA－Elman预测模型，为露天矿边坡变形预测提供一种有效途径。

1 模型算法原理

1.1 Elman原理及特点

1990年，Jeffery.L.Elman针对语音处理问题提出了Elman神经网络。它的输入包括有延迟的输入或输出数据的反馈，被视为一种反馈动力学系统［8－10］。

Elman神经网络的拓扑结构主要包含输入层、隐含层、承接层和输出层（见图1）。输入层的主要作用是传输信号；隐含层的主要作用是连接输出层和承接层的反馈，根据权值的调整影响输入的数据；承接层作为一步延时算子，能够使系统对历史状态的数据具有较强的敏感性，以达到记忆目的，增强网络本身处理动态信息的能力，实现动态建模；输出层的主要作用是线性加权输出。

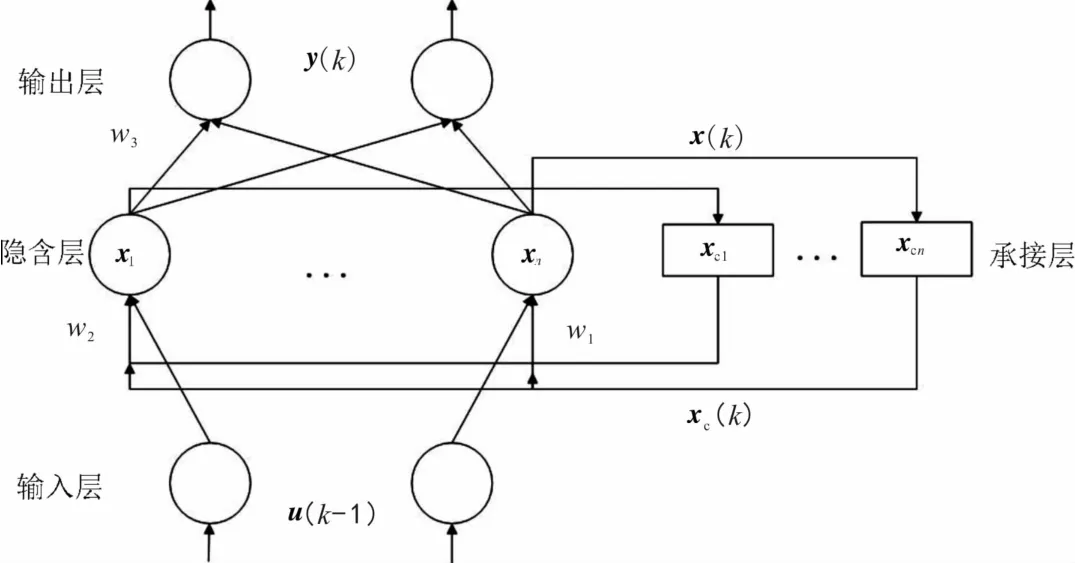
图1 Elman神经网络拓扑结构

Elman神经网络的非线性状态空间表达式为

式中：x为n维隐含层的节点单元向量；f（*）为隐含层神经元的传递函数；w1为承接层与隐含层的连接权值；w2为输入层与隐含层的连接权值；w3为隐含层与输出层的连接权值；xc为n维反馈状态向量；u为r维输入向量；y为m维输出节点向量；g（*）为输出神经元的传递函数，是隐含层输出的线性组合。

Elman神经网络采用传统的BP神经网络修正权值。误差函数的表达式为

式中di（k）为k时刻第i个输出节点的期望输出。

1.2 WOA优化Elman神经网络

WOA是一种元启发式优化算法，他源于对自然界中座头鲸群体狩猎行为的模拟，如鲸鱼群体搜索、包围、追捕和攻击猎物等过程实现优化搜索目的。相较于其他优化算法，WOA具有机制简单、参数少、寻优能力强等优点［11－12］。

传统的Elman神经网络初始权值和阈值一般通过随机赋值方式确定，缺乏全局搜索优化能力。本文采用WOA优化Elman神经网络的权值和阈值，增强Elman网络的训练速度及全局寻优能力。WOA优化Elman神经网络（WOA－Elman）算法流程如图2所示。

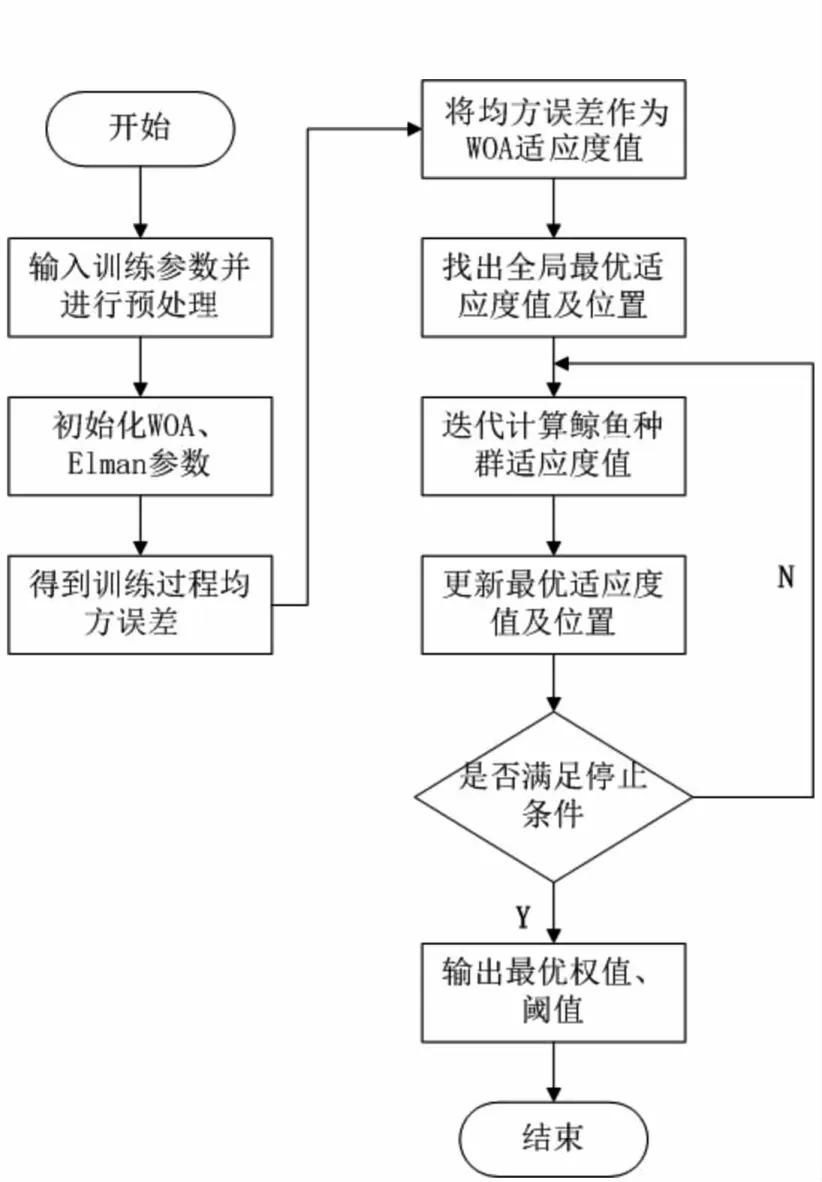
图2 WOA优化Elman神经网络算法流程

Step1：初始化Elman神经网络所需的参数。

Step2：初始化鲸鱼数量、最大迭代次数以及参数的上下限等WOA参数。

Step3：WOA通过包围猎物、螺旋式更新位置和搜索猎物，迭代优化Elman神经网络，直到迭代结束，形成最佳个体，包括权值和阈值。

Step4：分析最佳个体，利用分析的权重和阈值对Elman神经网络进行训练，并进行预测。

2 实例建模与验证

抚顺西露天煤矿位于辽宁省抚顺市，是我国第一大露天煤矿。该矿南帮边坡岩体破损、风化严重。本文以2016年1月至3月采用雷达系统监测的该矿南帮边坡位移80期数据［13］为例建立边坡位移预测模型。

2.1 构建WOA－Elman边坡位移预测模型

（1）数据预处理。

随着露天矿边坡演变阶段的不同，数据的变化差异较为明显。采用Elman神经网络预测时，各输入数据之间的量级差异偏大或者偏小均会影响预测结果。为了消除数量级与量纲方面的影响，防止出现神经元输出饱和现象，本文对所有原始数据进行归一化处理，使其均落在［0，1］区间。归一化公式为

反归一化公式为

式中：xmax为输入样本数据的最大值；xmin为样本数据的最小值；xi、yi分别为输入样本归一化前后的值。

（2）确定输入层节点数。

Elman神经网络输入层节点数对预测时效影响较大。若输入层节点数太大，Elman神经网络的训练时间长、结构冗余；若输入层节点数太小，会导致Elman神经网络不收敛。为此，本文采用滚动预测模式确定输入层节点数。所谓滚动预测即对每一周期的训练数据进行同步更新［14］。

以训练样本为例，抽取x1～xN组成第一个样本，其中（x1，x2，…，xN－1）为自变量，xN为目标函数值，以此类推，形成训练矩阵

本例中，分别选取3，4，5，…，20作为输入层节点数进行实时滚动。因输出为边坡预测值，故输出节点取1。不同的输入层节点数所对应的均方误差如图3所示。当N取值为3时，神经网络的均方误差最小，因此，选择3作为输入层节点数。

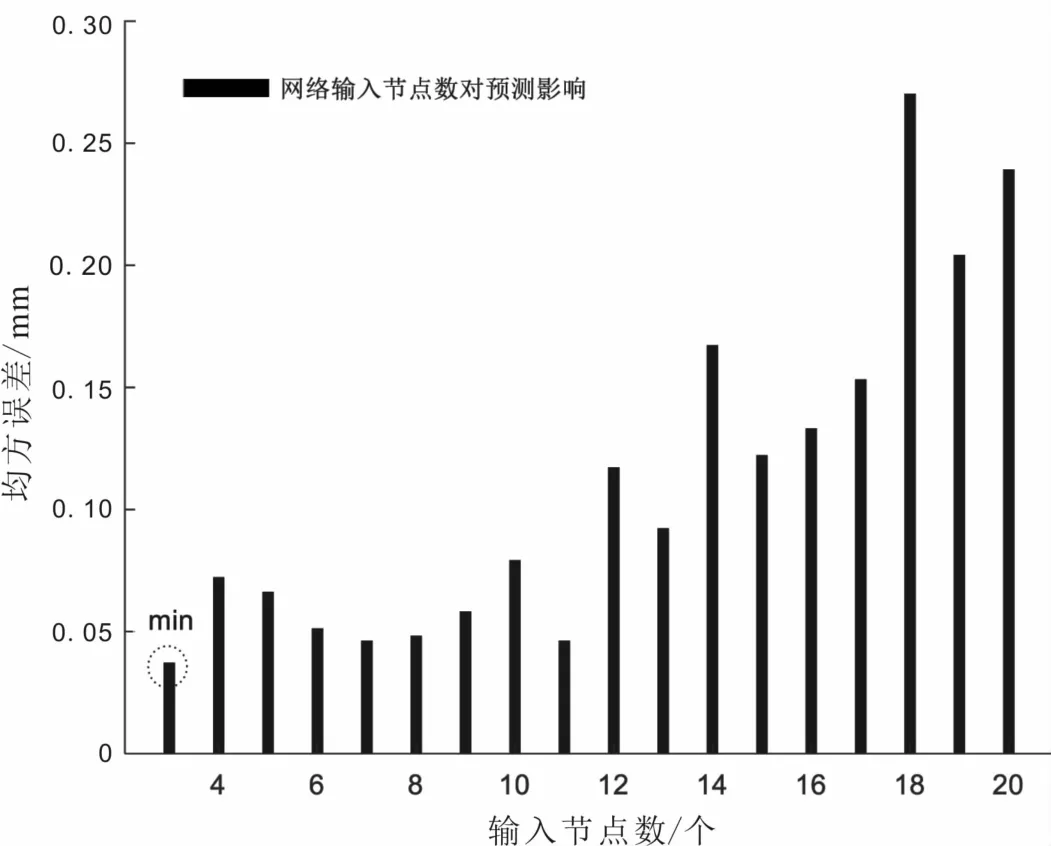
图3 本文输入层节点数与神经网络均方误差的关系

（3）选取激活函数。

选取常用的激活函数（purelin型、logsig型及tansig型）进行两两组合，求出不同组合下预测结果的均方误差（见表1）。

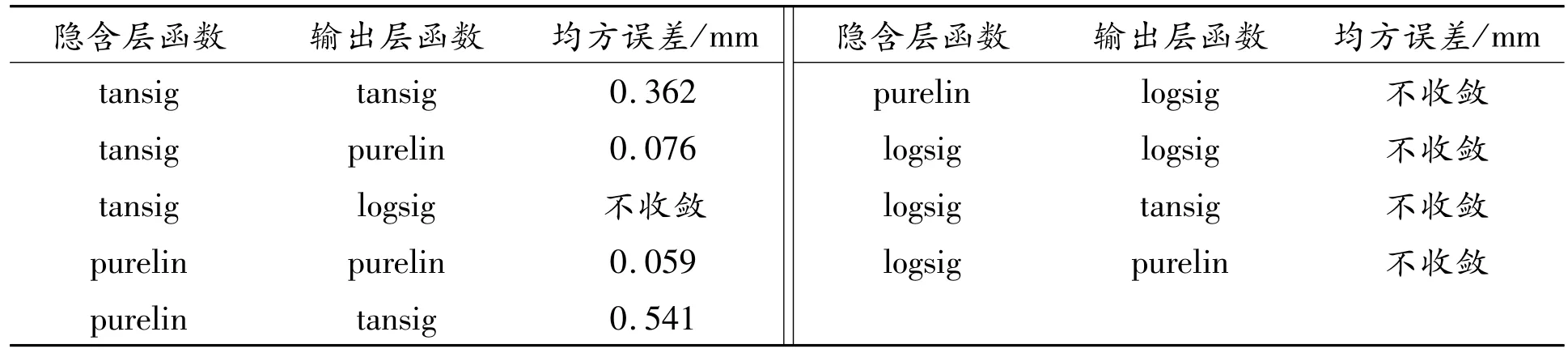
表1 不同激活函数组合预测结果的均方误差

由表1可知，当隐含层函数选取purelin、输出层函数选取purelin时，均方误差最低。因此，本文选其作激活函数组合。

（4）确定隐含层节点数。

隐含层节点数直接影响Elman神经网络的泛化能力。若隐含层节点数太大，则网络训练时间过长，会导致过学习现象，进而降低工作效率；若隐含层节点数太小，则难以建立复杂的映射关系，会导致逼近能力差。

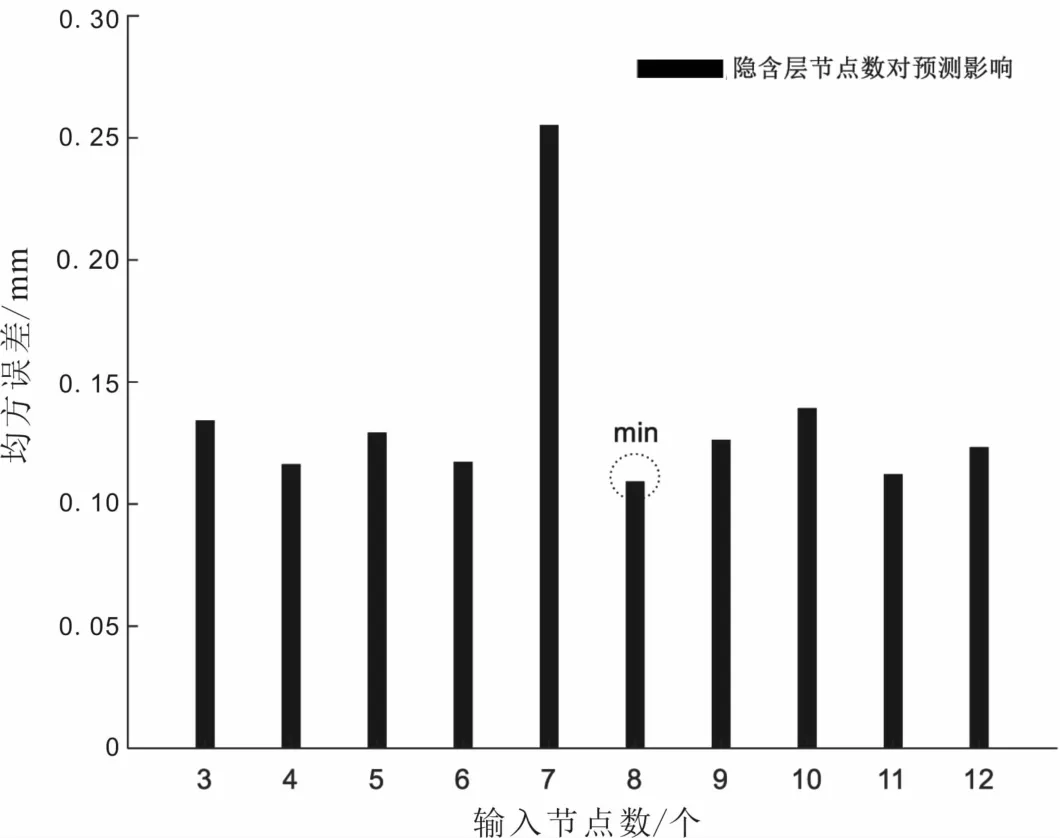
图4 本文隐含层节点数与神经网络均方误差的关系

2.2 3种模型的建模与预测性能对比分析

（1）3种模型建模。

分别采用3种神经网络对本文实例进行建模预测。将第1～58期数据作为训练样本，将第59～80期数据作为测试样本。

模型1（BP神经网络）。输入节点设为3，输出节点设为1，单隐含层，隐含层节点数设为6，隐含层、输出层的激活函数以及训练函数分别设为tansig、purelin、trainlm，学习速率设为0.01，目标误差设为0.000 1 mm，最大收敛次数设为2 000。

模型2（Elman神经网络）。输入节点数设为3，输出节点数设为1，单承接层、单隐含层、隐含层节点数均设为8，隐含层、输出层的激活函数均为purelin，训练函数设为traingdx，学习速率设为0.01，动量因子设为0.01，目标误差设为0.000 1 mm，最大收敛次数设为2 000。

模型3（WOA－Elman神经网络）。采用WOA获取Elman神经网络的最佳权值和阈值。初始化Elman神经网络所需的参数以及WOA参数（如鲸鱼数量、最大迭代次数以及参数的上下限等），再通过WOA包围猎物、螺旋式更新位置和搜索猎物操作，不断迭代寻找最优个体（包括权值w1、w2、w3和阈值b1、b2）。WOA的维数设为105，则存放最优个体的矩阵为1×105的权值矩阵。输入层到隐含层是8×3的权值矩阵，共24个权值。隐含层到承接层是8×8的权值矩阵，共64个权值。隐含层的阈值矩阵为8×1矩阵，共8个阈值。隐含层到输出层是1×8的权值矩阵，共8个权值。输出层的阈值矩阵为1×1的矩阵，共1个阈值。使用WOA得到的WOA－Elman神经网络最优初始权值和阈值如表2所示。

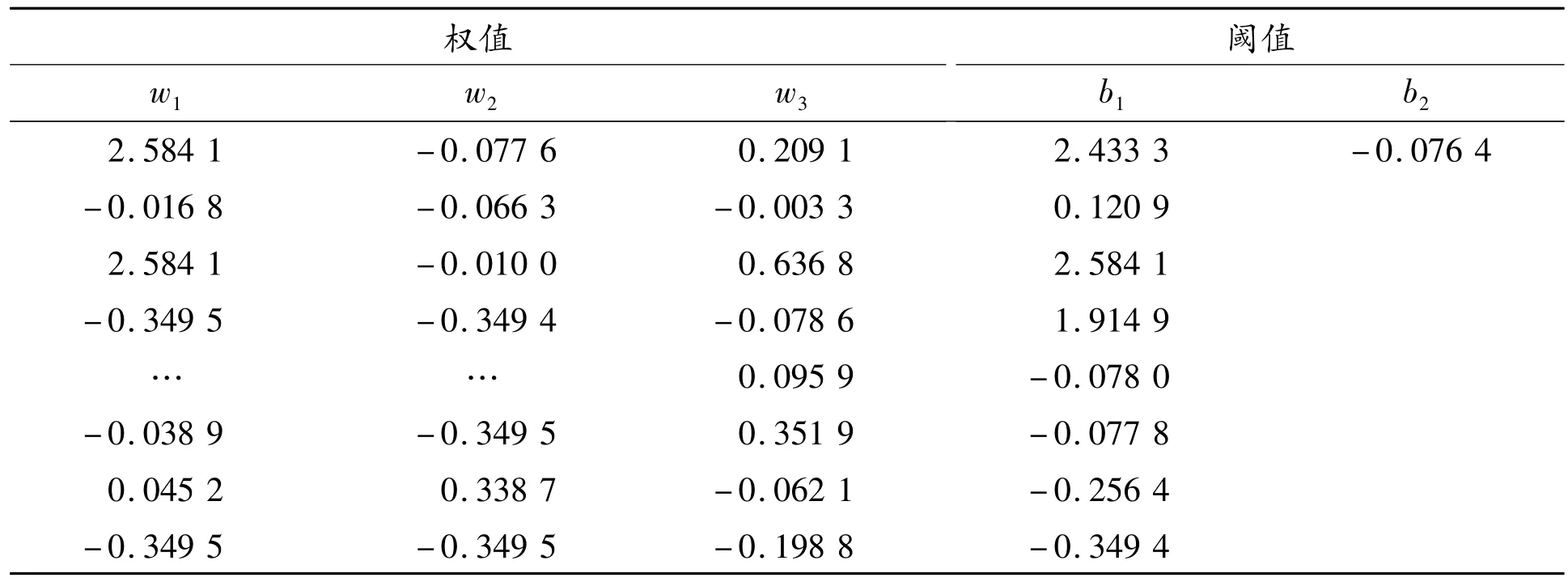
表2 WOA－Elman神经网络最优初始权值与阈值

（2）3种模型的预测性能对比分析。

采用3种神经网络对本文实例建模时，迭代次数越少，收敛速度越快。为了验证WOA－Elman神经网络的收敛性，在相同的训练样本下，比较WOA－Elman神经网络与Elman神经网络的收敛速度（此处不再讨论BP神经网络的收敛性）。WOA－Elman神经网络的进化曲线如图5所示。迭代过程可分为3个阶段：第0～10次进化迭代时，均方误差急剧减小；第10～23次进化迭代时，均方误差变化率逐渐减弱；第38次进化迭代后，进化曲线趋于平缓，并最终获得最优值。

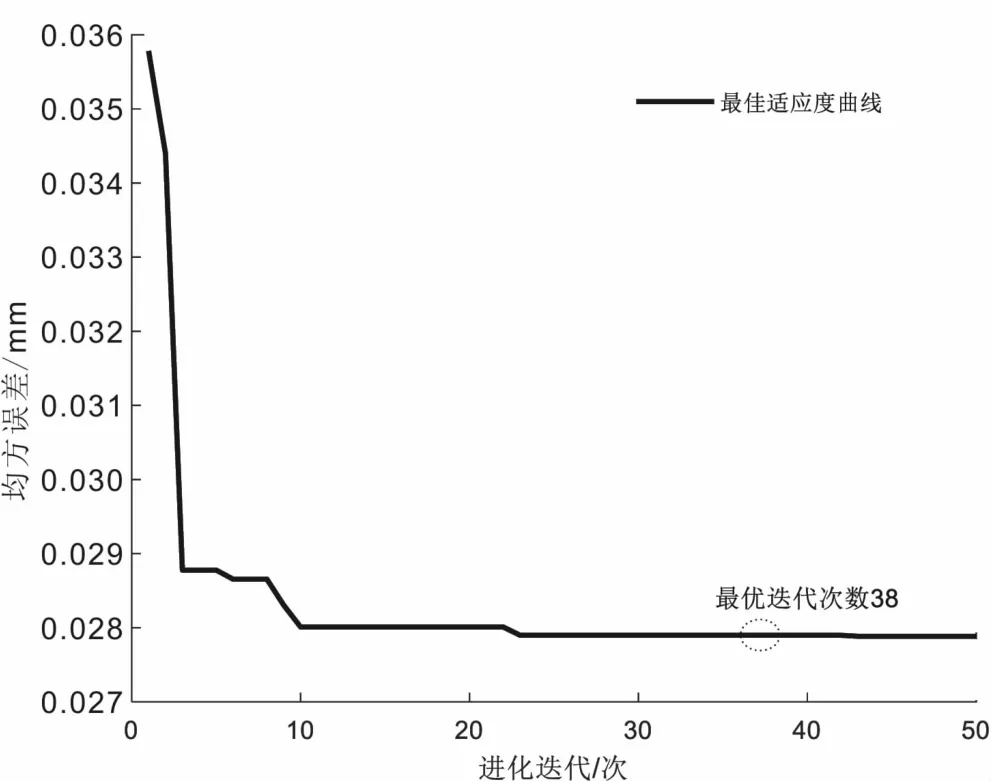
图5 WOA－Elman模型的进化曲线

样本相同时，Elman神经网络在迭代108次时才达到收敛，而WOA－Elman神经网络仅迭代38次，就达到了收敛，说明WOA－Elman神经网络收敛速度快。3种模型对测试样本的模拟测试结果及残差值如表3所示。

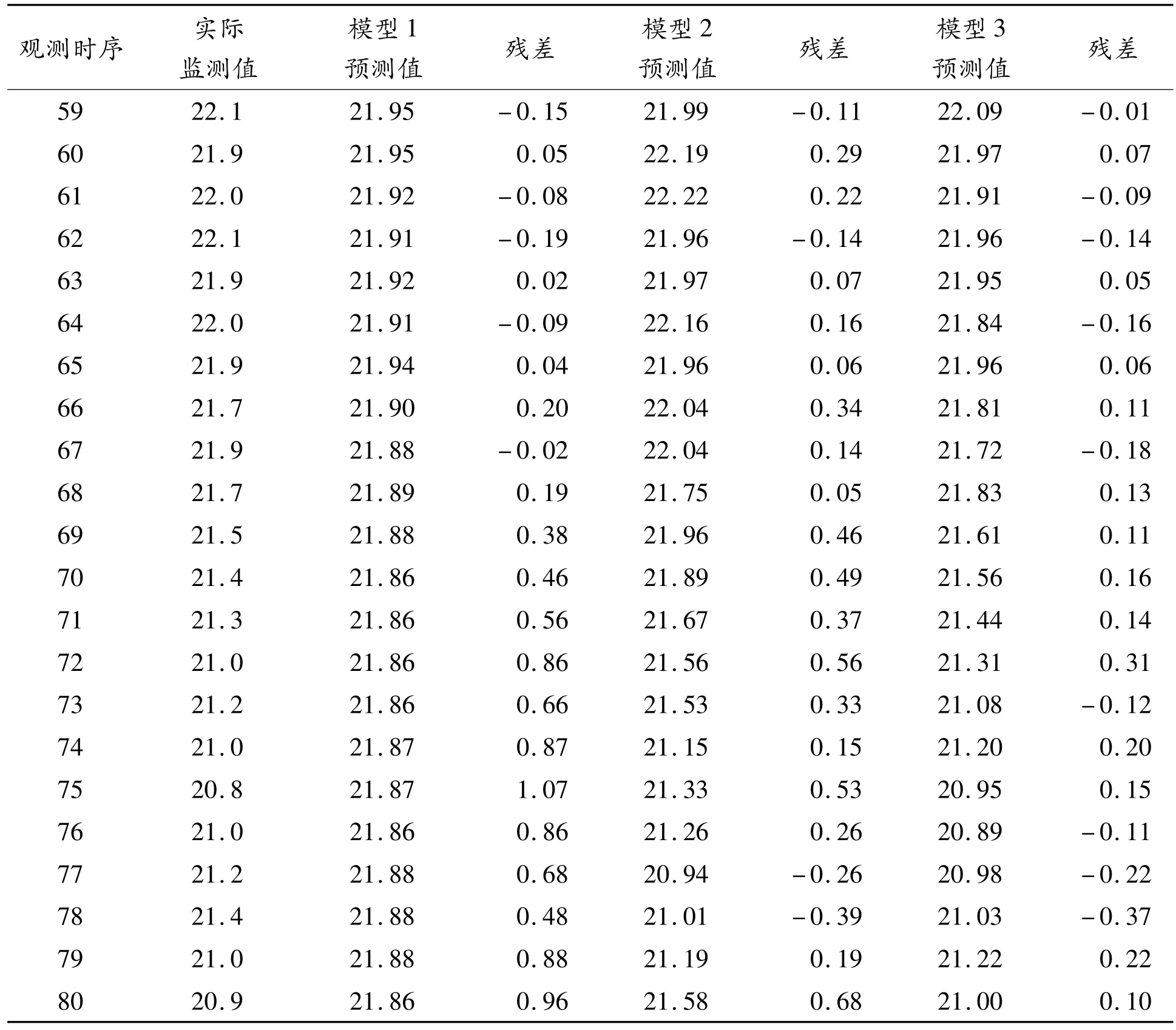
表3 3种模型对抚顺西露天矿位移的模拟测试结果mm

由表3可知，模型1的残差绝对值最大为1.07、最小为0.02；模型2的残差绝对值最大为0.68、最小为0.05；模型3的残差绝对值最大为0.37、最小为0.01。这说明模型3的测试结果较稳定，波动性小。选取均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）等指标评价各模型，评价结果如表4所示。

表4 3种模型对抚顺西露天矿位移预测的测试结果精度

由表4可知，模型3的MAE、RMSE和MAPE分别为0.146 mm、0.167 mm及0.685%，与其他两种模型的预测结果相比，具有较小的预测误差，与模型2的MAE、RMSE、MAPE相比，分别降低了0.137 mm、0.165 mm、0.647%。因此，模型3的稳定性更好，预测精度更高，泛化能力更强。