作动器故障下的无人机容错控制方法

崔玉伟，孙 雪

（1.航空工业西安飞行自动控制研究所飞行控制系统部，陕西西安 710000；2.飞行控制航空科技重点实验室，陕西西安 710065）

0 引言

美军曾提出1种面向无人机集群作战体系设计的一体化框架，构建无人机集群“使命—战术—行动—算法—数据”5层任务框架[1-2]，集群作战能够形成单一作战平台所不具有的独特作战优势而被广泛研究[3-6]。近几年随着无人系统在有人/无人协同、集群两大技术领域的应用推进[7-10]，无人系统不再是低廉、高风险的代名词，反而越来越强调2个方面的技术要求：一是低成本，二是高容错。无人机执行任务过程中，其传感器、作动器可能出现故障，无法正常飞行。为保障飞行过程中的安全性[11-12]，容错控制成为国内外研究学者的重点研究方向之一[13]。

针对飞控系统传感器、舵机的故障诊断与容错控制方法有很多，而对于无人机飞控系统传感器的故障，可以采用基于模型的故障检测、隔离和调节方法进行低余度/无余度信号的重构，以解析余度的方式解决传感器信号的容错问题[14]。

与传感器故障不同，针对舵机的故障，基于模型的故障检测与隔离方法，不能解决伺服驱动的问题，必须通过飞机其他舵面的控制补偿进行重构，以达到容错控制的目标。当前有很多学者提出自适应控制算法，以解决舵面故障情况下的各种自适应控制问题[15]，达到飞行控制目标。然而，这些算法的实时性普遍受到质疑，而且大部分算法需要精确的数学模型。因此，目前针对舵机故障的容错控制问题，工程上更多的还是基于故障检测的结果。首先，进行故障舵机的隔离，避免其故障蔓延；其次，通过重新调整控制器的参数，或者改变控制器的结构，保证故障后系统的稳定性和控制性能。但是这种方式必须是离线计算出多种故障下所需的控制律参数，并将这些参数提前存储在飞控计算机中。在飞行过程中，根据故障检测得到的故障信息，选择匹配的控制律参数，得到对各种故障模式下的重构飞行控制律。由于重新调整的控制律参数是离线设计好的，重构飞行控制律只对事先考虑到的故障模式具有容错能力，这就限制了这种方法的扩展性[16]。

目前，对于中小型无人机，基本上都是采用电动舵机作为驱动机构；而对于大型无人机，随着大功率电动舵机的不断成熟，替代液压舵机的趋势也在不断加快。电动舵机的故障模式主要有2 种：多种原因或故障导致的舵机回中和输出卡死。从舵面控制的角度来说：第1种回中的情况影响较小，重要的是实现故障检测，能够做到快速发现故障；而第2种输出卡死的情况更加复杂，因为它会带来附加的操纵力矩，在飞行控制中需要优先平衡附加操纵力矩。

综上，针对无人机舵机的多种故障模式，本文提出反步法控制结合基于线性规划方法的控制分配策略，不需要重新调整控制律参数，只需根据故障情况，改变其控制分配矩阵，即可实现无人机舵机故障的容错控制。

1 系统方程

某型无人机采用常规布局，可独立操纵的舵面包括左全动平尾、右全动平尾、副翼和V 型方向舵。由于左、右全动平尾可以独立控制，也就是说除了可以同向偏转产生俯仰力矩外，还可以差动偏转产生滚转力矩，这就在横侧向提供了额外的控制力矩。同时，V型方向舵也产生了额外的俯仰力矩。因此，该布局无人机的多操纵面特性为舵面故障后的补偿控制提供了条件。

在机体轴坐标系下的飞机姿态动力学方程如下：

式（1）中：α、β、μ分别为迎角、侧滑角和滚转角；p、q、r分别为俯仰角速率、偏航角速率和滚转角速率。

式（2）～（7）中：m为质量；V为速度；γ为航迹角；T为发动机推力；D、L、Y分别为阻力、升力和侧向力。

式（8）～（10）中：S为机翼面积；qˉ为飞行动压；cd、cl、cy分别为阻力系数、升力系数和侧向力系数。

2 容错控制器设计

2.1 反步法最优控制器设计

现有二阶非线性系统为：

针对上述系统，设计其反步法控制器步骤如下。

步骤1 针对式（11）中x1子系统，以x2为控制输入，设计虚拟控制律。选择如下的控制律形式：

构建Lyapunov函数：

则当x2=时，其微分为W=(ϕ(x1)-ψ(x1))x1，当满足(ϕ(x1)-ψ(x1))x1＜0 时，可以保证其负定。

步骤2 引入误差变量：

系统（11）就变换为：

构建控制Lyapunov函数：

式（16）中，F(x1)是x1子系统任意一个有效的控制Lyapunov函数，也就意味着，当x2=时：

式（17）中，U(x1)为正定的。

选择F′(x1)=-ψ′(x1)(ϕ(x1)-ψ(x1))，F( 0)=0 可以使得第二项中含x1的项目彼此抵消。

将F′(x1)代入到式（17）中，可得：

当满足ψ′(x1)＞0 时，可以保证其正定。

此时的系统Lyapunov函数为：

为了使得V负定，可以选择控制律：

当满足k ＞ψ′(x1)时，可以保证V=-U(x1)-(k-ψ′(x1))负定。

之后，再确定满足它的最优价值函数，对比式（15）所示的误差系统与式（11）所示的二阶系统，可以得到：

而且，

因此，代入式（18）（19）就可以得到控制律式（22）所能达到的最优控制性能参数：

为了使得Q(x)为正定，代价函数为有意义的最优性能，必须保证：

因此，结合式（19）（21）（27），可以得到：当满足0＜k1＜k2＜2k1时，可以使得系统原点具有全局渐近稳定性。并且使得如下的最优价值函数最小：

考虑由式（1）的动力学方程，引入如下坐标变换：

对应的动力学方程就变为：

因此，以坐标变换后的角加速度为控制输入，可以得到三轴的解耦二阶非线性系统如下。μ通道模型：

α通道模型：

β通道模型：

可以发现式（31）～（33）和式（11）的结构完全一致，因此，得到三通道的反步法最优控制器。

μ通道控制器：

同时可以使得如下的最优价值函数式（34）最小：

α通道控制器：

同时可以使得如下的最优价值函数最小：

β通道控制器：

同时可以使得如下的最优价值函数最小：

2.2 基于控制分配的容错控制器设计

随着无人机在空中作战体系中的作用越来越重要，它所承担的任务也越来越复杂，需要承受一定的故障影响，具备良好的容错能力。对于飞控系统而言，由于无人机具有多操纵面特性，特别是多冗余特性的操纵面的引入，为无人机舵机故障后的重构控制提供了先决条件。

当故障检测模块发现电动舵机出现回中或者位置卡死的故障模式时，控制分配模块将由正常模态切换到故障模态，此时控制分配模块接收控制律模块后解算得到的舵机控制指令将体现故障模式的影响。对于非线性系统，设其运动方程为：

式（40）中，f:ℝ×ℝk↦ℝn，g:ℝn×ℝm↦ℝk均为非线性环节，且k ＜m。

式（40）可以写为以下形式：

式（41）中，Bv∈ℝn×k，f和g具有以上相同的映射形式。引入虚拟控制量：

式（42）中，v∈ℝk，则系统的状态方程可重写为：

这样式（41）就可以转化为式（42）（43）的形式。也可以利用控制分配问题的标准形式来进行研究，这就是针对非线性系统的非线性控制分配问题。可以看出，与线性控制分配问题所不同的是，映射g为非线性形式g(x,u)。

在飞控制系统中，控制分配是要求实时解算的，而对于v=g(x,u)这一类的非线性控制分配问题尚无法实现实时解算。因此，解决这一问题的方法之一是利用局部逼近映射的方法，用线性映射来近似非线性映射。通过局部泰勒形式展开g(x,u)，在u0点处进行线性化可以得到：

这样，引入线性映射B(x)=(x,u0)，也称为控制效率矩阵，就把非线性控制分配问题（42）归结为线性控制分配问题：

转化为线性控制分配问题后，它的求解有很多方式。基于线性规划的优化算法，凭借其较低的运算成本和单纯形法解法，在控制分配问题的求解过程中，有着广泛的研究[17]。根据前期的研究成果[18]，这里直接应用基于线性规划的分配算法。

结合式（45）（46），给出控制分配问题的描述。

因此，线性规划问题可以用下面的矩阵来定义：

优化目标为：

δ0可以选择为上一采样时间的控制输入u(t-T)。如果考虑到控制效率矩阵选取的局部性特点，当控制效率参数不是单调变化时，可能在某些点处出现B中某一列为0的状况，使得不能满足矩阵满秩的条件，无法求得控制分配解。因此，选择在某一个固定点处展开，比如δ0=0 处。

步骤2 计算泰勒线性展开修正后的虚拟控制输入：

步骤3 利用式（47）的控制分配方法求解公式得到式（49）（50）的控制分配问题的解。

下文将针对前文所述的电动舵机可能出现的回中或者位置卡死的2 种故障模式，依据上述的控制分配设计方法，进行容错控制方案的描述。

如式（51）所示，其为正常情况下飞机的非线性系统方程描述。

式（51）中，g(x,u)表示各舵面对系统的控制效率，当舵机导致舵面发生故障时会发生变化，给出了故障情况下飞机的非线性系统方程描述：

式（52）中：gf(x,uf)为故障情况下系统的控制矩阵，uf∈ℝn为故障时的控制输入。针对不同的故障模式，式（52）对应不同的函数形式。

根据重构控制要求，控制分配需要实现的是g(x,uf)=gf(x,uf)。

对于正常情况下的控制分配问题，其分配目标是：

线性化处理后：

对于故障情况下的控制分配问题，其分配目标是：

同样进行线性化处理：

2.3 故障模式

2.3.1 故障模式1：舵机位置卡死

位置卡死是指由于电机堵转或其他机械原因导致的舵机处于某一个固定位置的故障模式，它可以由故障检测模块来实现。在这种故障模式下，与舵机相连的舵面也会卡在某一位置。这样的话，它的偏转不但不能产生预期的控制效果，而且还会产生不希望的额外的附加力和附加力矩。因此，必须在控制分配中抵消卡死的舵机产生的影响。

当舵机卡死时，飞机的运动方程并没有改变，飞机方程如式（52）。其中，非线性控制环节满足gf(x,u)=g(x,u)。因此，经过线性化后控制效率矩阵满足Bf(x)=B(x)。

根据式（58）控制分配对重构控制的求解可得：

式（59）中：假设无人机拥有m个舵面，=(δ1,δ2,…,δj,…,δm-1)∈ℝm-1；为Bf中除去卡死的舵面后剩余的控制效率矩阵；bj为该卡死的舵面的控制效率系数；δf为故障舵面的卡死位置。

进一步推导得到：

式（60）中：第一项将原来舵面需要分配的转矩重新分配到剩余的有效舵面上；第二项用来抵消卡死的舵面造成的附加影响，这样就得到卡死时舵面的实际输出为：

2.3.2 故障模式2：舵机回中

舵机回中指由于各种故障导致离合器切断电流控制输出，进而使得舵机没有输出力的故障模式，它可以由故障检测模块来实现。在这种故障模式下，与舵机相连的舵面也会处于松浮状态，也就是该舵面的控制效率为0。此时，可以假设松浮的舵面并不会对飞机产生任何气动力和气动力矩，也就是操纵面对飞机的控制输入产生的作用为0。

与故障模式1 相似，舵机回中时飞机的状态方程没有发生变化，即故障前后控制效率矩阵Bf(x)=B(x)，仅仅是松浮的舵面的控制输入为0，引起的控制能力损失需要由剩余的有效操纵面来补偿。

式（62）中：假设无人机拥有m个舵面，=(δ1,δ2,…,δj,…,δm-1)∈ℝm-1；为Bf中除去松浮舵面后剩余的控制效率矩阵；bj为该松浮舵面的控制效率系数；δf为松浮舵面对应的控制输入。与卡死舵面不同之处在于，松浮的舵面只是随着飞机的飞行成漂浮状态，认为控制输入δf=0。

进一步推导得到：

这样就得到舵机回中时的舵面实际输出：

3 仿真验证

综合2.1 和2.2，对该无人机模型进行数值仿真。其中，该无人机4个舵面，即副翼、左升降舵、右升降舵和方向舵的特性限制如下。

偏转位置限制：

偏转速率限制均为：

第2章中所述的最优控制器的参数为：kα=3.65、kq=5.46、kβ=3.5、kr=4.7、kμ=5.32、kp=7.63。

针对舵机的2 种故障情况（卡死在5°、回中在0°）下的三轴机动运动的容错控制的数值仿真。在仿真中，反步法最优控制律的形式和参数都不改变，需要改变的仅仅是控制分配中的分配算法切换。

同样考虑三轴机动运动，给定指令输入：

仿真图1～4 给出了方向舵的舵机位置卡死在5°和回中2种故障模式下的仿真结果。

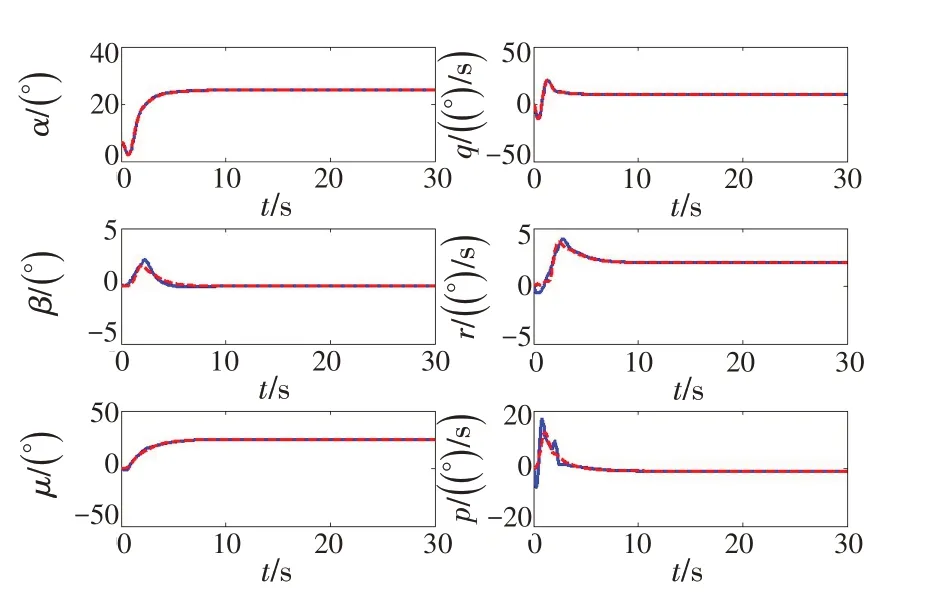
图1 方向舵卡死后容错控制响应对比Fig.1 Comparison of fault-tolerant control response after rudder stuck

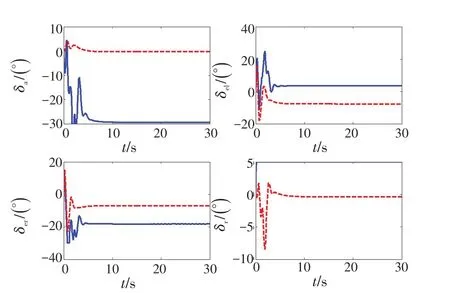
图2 方向舵卡死后操纵面偏转对比Fig.2 Comparison of steering surface deflection after rudder stuck

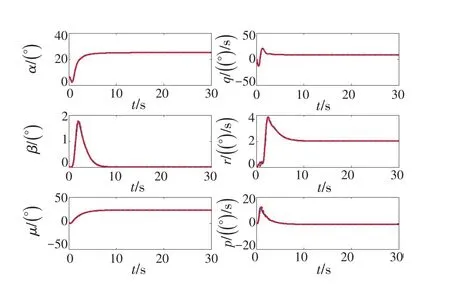
图3 方向舵松浮后容错控制响应对比Fig.3 Comparison of fault-tolerant control response after rudder loosening

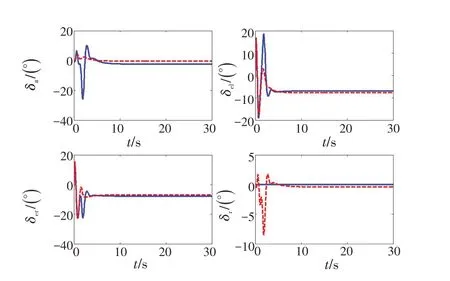
图4 方向舵松浮后操纵面偏转对比Fig.4 Comparison of steering surface deflection after rudder loosening

可以看出，当出现这2种典型的舵机故障时，利用控制分配方法进行重构设计后，剩余舵面很好地补偿了故障舵机所连接的舵面的控制影响，迎角和滚转角快速地跟踪响应，且稳定性能好，基本没有侧滑角，各个操纵面均处于约束范围内，控制分配的设计很好地完成了重构控制的任务，获得了良好的控制效果，达到了容错控制的目标。

4 结论

本文针对常规布局无人机的舵机故障：首先，进行故障分类和建模；其次，设计1种反步法和控制分配结合的容错控制器；最后，在无故障和舵机有故障的情况下进行仿真验证。无故障情况下，本文所设计的反步法最优控制器和基于线性规划方法的控制分配策略能在5 s内控制无人机系统稳定。舵机有故障情况下，分别在舵机卡死和回中的模式下进行仿真，所设计的容错控制器利用控制分配方法进行重构控制，取得了良好控制效果，实现了容错控制目标。