航空发动机风扇盘破裂试验中心拉杆预紧力分析
2024-01-10刘引峰范潘潘高小新庄周柱
刘引峰,范潘潘,高小新,庄周柱,袁 胜
(中国航发湖南动力机械研究所,湖南 株洲 412002)
1 引言
轮盘是航空发动机的重要部件,其性能直接影响发动机的可靠性和安全性。根据国家军用标准[1],轮盘必须进行破裂试验。轮盘破裂试验一般在立式轮盘试验器上进行,但是由于轮盘无法与立式轮盘试验器驱动装置直接连接,故需设计专用工装。专用工装的设计应尽可能模拟轮盘在发动机的连接形式,且不能对轮盘有明显的加强和削弱作用。对于空心且两端均有定心结构的轮盘,其破裂试验专用工装宜采用中心拉杆预紧的连接结构形式。为保证轮盘破裂试验中各零件连接稳定、可靠,需在装配时对中心拉杆施加合适的预紧力。预紧力过小,零件之间出现松动,连接不可靠;预紧力过大,零件的强度储备不足。因此,中心拉杆预紧力是否合理,是这类轮盘破裂试验是否成功的一个关键因素。
一些学者对转子的轴向预紧力或松弛力进行过有益的探索与研究。如尹泽勇等[2-4]以端齿连接转子为研究对象,利用弹性力学、壳体理论、有限元素法及多变量函数插值技术等手段,给出了离心力、气动力、热载荷及机动载荷等在各端齿接触面处引起的轴向松弛力或压紧力的计算公式。郭飞跃等[5]采用MSC/MARC 分析软件,确定了某涡轴发动机组合压气机转子中心拉杆和小拉杆的轴向预紧力。范潘潘等[6]采用分段圆筒的简化思路,对带止口定心传扭结构高速转子轴向预紧力进行了估算。张春雷[7]、李辉光[8]等对拉杆转子的轴向预紧力进行了分析。总结前人的研究发现,对于航空发动机中心拉杆预紧连接形式的轮盘破裂试验,其中心拉杆预紧力的理论确定还没有公开的研究报道。
本文针对某航空发动机风扇盘破裂试验中心拉杆预紧力进行理论研究。采用分段圆筒的简化方法,利用材料力学和弹塑性力学理论,推导了中心拉杆预紧力的计算公式,并与ANSYS Workbench 有限元分析软件计算出的中心拉杆预紧力进行对比,分析了产生误差的原因,提出了提高解析法计算精度的措施。其研究成果可为同类型航空发动机轮盘强度试验中心拉杆的结构尺寸优化和中心拉杆预紧力的确定提供参考依据。
2 风扇盘破裂试验专用工装结构设计
风扇盘破裂试验专用工装是连接风扇盘和立式轮盘试验器的转接结构,其设计应考虑风扇盘在发动机上的连接形式以及立式轮盘试验器驱动装置接口尺寸,并且需要有可靠的定心。由于风扇盘为空心结构,且两端均有定心圆柱面,所以采用中心拉杆预紧连接形式的专用工装,其结构示意图见图1。图中,风扇盘与压块、风扇盘与轴均采用圆柱面过盈连接定心,轴与中心拉杆、中心拉杆与螺母均采用螺纹连接,压块与中心拉杆为小间隙配合。

图1 专用工装结构示意图Fig.1 Structural diagram of special tooling
3 风扇盘破裂试验的试验工况
由于风扇盘实际工作状态下的平均温度约为80℃,而这一温度对风扇盘材料力学性能影响较小,故破裂试验选择在室温下进行。室温下的风扇盘破裂试验等效转速根据试验状态与实际工作状态子午截面破裂转速裕度相当的原则[9]得到。本文中心拉杆预紧力的分析只考虑离心载荷的影响。
4 中心拉杆预紧力解析分析
4.1 模型简化
由于风扇盘不是对称结构,为简化计算,在保证风扇盘的质量、质心位置和相对轴向的转动惯量等惯量参数相同的前提下,将风扇盘简化为风扇模拟盘。采用分段圆筒简化方法,按半径变化进行分段,保证各圆筒的质量和相对于轴向的转动惯量与对应部分一致。简化后的模型见图2。

图2 简化计算模型Fig.2 Simplified calculation model
在静止装配状态下,压块和风扇盘被压缩,中心拉杆被拉伸。为便于阐述变形过程,被压缩部分简称A 部件,见图2 中蓝色虚线框部分。A 部件从左往右共有9 个圆筒,根据线性叠加原理,A 部件在离心载荷作用下轴向长度的变化量等于各圆筒轴向长度变化量的叠加。被拉伸部分简称B 圆筒,见图2 中红色虚线框部分。
4.2 模型材料性能参数
风扇盘材料采用钛合金,密度4 480 kg/m3,弹性模量123 GPa,泊松比0.33。专用工装各零件材料均采用高温合金,密度8 240 kg/m3,弹性模量204 GPa,泊松比0.30。
4.3 离心载荷作用下的轴向变形量
假设圆筒(如图3 所示)内径为 ar,外径为 br,长度为l,且以等角速度ω旋转。由弹性力学公式[10]可知,圆筒中半径r处的径向应力σr、周向应力σθ分别为:
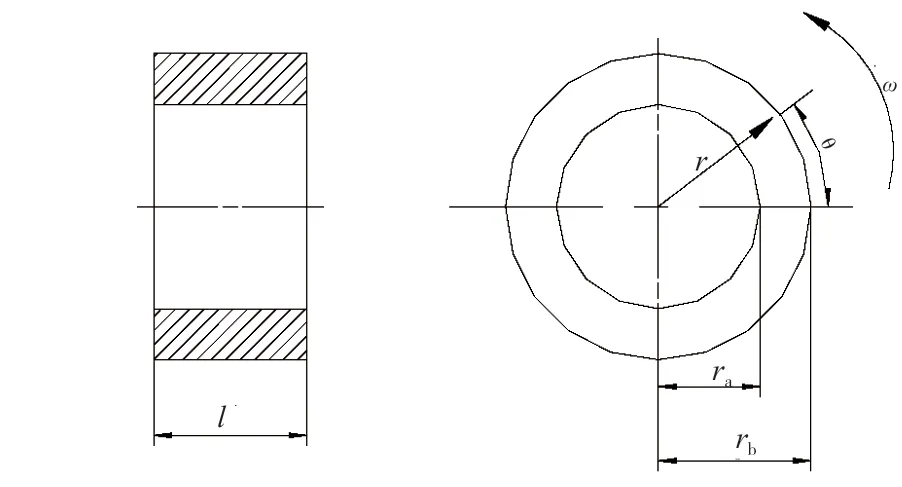
图3 圆筒结构示意图Fig.3 Structural diagram of cylinder structure
式中:ν为泊松比。
根据弹性本构方程[10],轴向应变εz为:
假设应力不超过比例极限,则圆筒轴向长度变化量Δl为:
根据公式(1)、(2)、(4)和线性叠加原理,可得A 部件轴向长度的缩短量lA为:
式中:ΔlAi表示第i个圆筒轴向长度缩短量;σri表示第i个圆筒在半径r处的径向应力;σθi表示第i个圆筒在半径r处的周向应力;rAai、rAbi、lAi、rAi、Ei、νi分别表示第i个圆筒的内径,外径,轴向长度,半径,弹性模量和泊松比,且取。
4.4 离心载荷作用下风扇盘及专用工装的变形协调过程
在弹性范围内受多种载荷作用的零件变形,其最终变形状态与施加载荷历程无关,因此,将变形过程分解,每一步施加一种载荷。变形协调过程见图4。

图4 变形协调示意图Fig.4 Diagram of deformation compatibility
变形分析过程如下:
(1) 各零件在静止装配状态下,由于受中心拉杆预紧力作用,A 部件被压缩,B 圆筒被拉伸,变形后的位置为P11Q。
(2) 各零件受离心载荷作用时,径向长度伸长,轴向长度缩短,且A 部件的轴向长度缩短量lA大于B 圆筒轴向长度缩短量lB,变形后的位置为P2Q2。
(3) 为了达到变形协调,A 部件在步骤(2)的基础上轴向长度伸长,伸长量为ΔlA,B 圆筒在步骤(2)的基础上轴向长度缩短,缩短量为ΔlB,此时轴向力的减小量为ΔF(即中心拉杆的松弛力),最终变形后的位置为P33Q。
根据变形协调过程,满足以下变形协调方程:
4.5 风扇盘破裂试验中心拉杆预紧力计算公式
根据胡克定律和线性叠加原理,可得A 部件轴向长度的伸长量ΔlA为:
式中:AAi表示第i个圆筒的横截面面积。
同理可得,B 圆筒缩短量ΔlB为:
式中:lB、AB分别表示B 圆筒的轴向长度和横截面面积,EB表示B 圆筒材料的弹性模量。
为了保证工作时各连接面不脱开,要求中心拉杆预紧力大于工作时的最大松弛力,并留有一定裕度。中心拉杆预紧力 0F应满足:
式中:N表示紧度储备系数。
根据式(5)~(9),可得风扇盘破裂试验中心拉杆预紧力的计算公式:
4.6 中心拉杆静强度校核
中心拉杆为满足静强度要求,屈服强度储备系数KS和极限强度储备系数Kb应满足:
式中:σ0.2为材料屈服强度,σb为材料极限强度。
σmax取中心拉杆最小工作截面的平均拉伸应力。根据中国航空材料手册[11],中心拉杆材料的屈服极限为1 030 MPa,极限强度为1 280 MPa。将数据代入式(11)和(12)可得,中心拉杆预紧力需满足公式:
式中:rz为中心拉杆最小截面处的半径。
5 中心拉杆预紧力有限元分析
利用ANSYS Workbench 有限元分析软件,计算某航空发动机风扇盘破裂试验中心拉杆的预紧力。
5.1 计算模型
除风扇盘叶片外,风扇盘体与专用工装均为轴对称结构,为了节省求解时间,选用二维分析。风扇盘体、中心拉杆、压块、螺母、轴采用轴对称单元,风扇盘叶片采用带厚度平面应力单元。建立的二维计算模型如图5 所示。用八节点四边形单元划分网格,划分网格后的计算模型包括23 700 单元,73 123 个节点。

图5 二维计算模型Fig.5 2D calculation model
5.2 计算参数
风扇盘和专用工装各零件的材料性能参数见4.2 节。
5.3 边界条件
根据风扇盘与专用工装各零件之间的配合关系设置边界条件:①约束中心拉杆左端面的轴向位移;②中心拉杆与螺母、中心拉杆与轴之间定义轴向耦合;③风扇盘与压块、风扇盘与轴配合面处的圆柱面定义过盈连接,过盈量与风扇盘在发动机中的过盈量一致;④风扇盘与压块、风扇盘与轴设置轴向接触。
5.4 载荷施加
试验中只受离心载荷作用。载荷施加方式为:①离心力以转速形式施加;②中心拉杆预紧力通过压块和螺母的轴向接触面定义轴向过盈,过盈量选为0.257 mm。
5.5 中心拉杆预紧力有限元计算步骤
中心拉杆预紧力由工作时中心拉杆的松弛力求得。中心拉杆的松弛力分2 步求解:第1 步,在静止装配状态下,在压块与螺母的轴向接触面处施加轴向过盈(过盈量根据轮盘的变形情况确定),计算得到压块与螺母之间的轴向力 1F;第2 步,在第1 步的基础上,施加离心载荷,计算得到压块与螺母接触面之间的轴向力 2F,1F与 2F之间的差值即为中心拉杆松弛力ΔF。
6 解析法与有限元法计算结果对比分析
解析法:将专用工装各零件的相关数据、材料参数、紧度储备系数(N取1.25)以及室温下风扇盘破裂试验等效转速代入式(10),可得到中心拉杆预紧力为16 584.2 N。
有限元法:在静止装配状态下,计算得到压块与螺母之间的轴向力为41 397 N;施加离心载荷后,得到压块与螺母之间的轴向力为28 639 N,中心拉杆的松弛力为12 758 N。N取1.25,计算得到中心拉杆预紧力为15 947.5 N。
解析法与有限元法计算结果对比见表1。从表中得出,解析法与有限元法的计算误差为3.84%。产生误差的主要原因是:第一,解析法将结构复杂的风扇盘离散成各个圆筒的组合,与风扇盘的实际结构有区别;第二,解析法中风扇盘轴向长度的变化量等效为各个对应圆筒内外径平均值处轴向长度变化量的叠加,与风扇盘在工作状态下的实际轴向长度变形有区别。
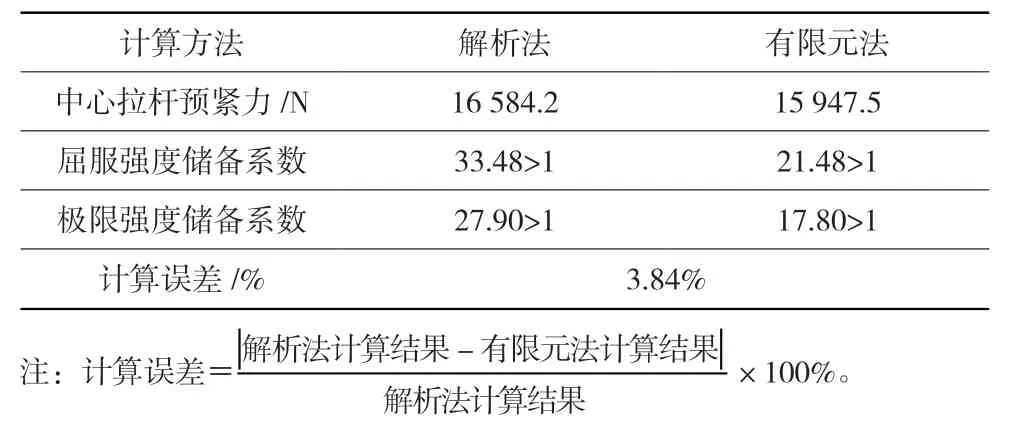
表1 解析法与有限元法计算结果对比Table 1 Comparison between calculation results by analytical method and infinite element method
为提高解析法的计算精度,可采取如下措施:将风扇盘沿半径变化简化成尽可能多数量的圆筒,不断修正计算模型,进一步还原风扇盘的结构形状,减小因模型简化带来的计算误差。
7 结论
分别采用解析法和有限元法,对涡扇发动机风扇盘破裂试验中心拉杆的预紧力进行了理论分析,主要结论为:
(1) 基于弹性力学和材料力学理论,推导出了航空发动机风扇盘破裂试验中心拉杆预紧力与风扇盘和专用工装结构尺寸、风扇盘破裂试验等效转速之间的关系。
(2) 采用有限元法,利用ANSYS Workbench 软件计算了风扇盘破裂试验中心拉杆预紧力,并通过对比解析法和有限元法计算结果,分析了产生误差的主要原因,提出了提高解析法计算精度的方法。
(3) 解析法能够清晰地分析出中心拉杆预紧力与风扇盘破裂试验等效转速、中心拉杆尺寸等相关参数之间的关系,对于中心拉杆结构优化和尺寸调整具有重要的理论参考价值。
(4) 有限元法能够更精确地考虑复杂结构,适合于定量计算分析。
