小管径顺排管束单元换热特性实验研究

覃扬佳，闻 洁，亓少帅

(1.北京航空航天大学 能源与动力工程学院，北京 100191；2.北京航空航天大学 航空发动机气动热力国防科技重点实验室，北京 100191；3.北京航空航天大学 杭州创新研究院(余杭)，杭州 311100；4.北京航空航天大学 航空发动机研究院，北京 100191；5.中国航天科技集团有限公司中国航天空气动力技术研究院，北京 100074)

1 引言

航空发动机性能提升主要通过提高涡轮前温度与压气机增压比来实现，而提高涡轮前温度会加重涡轮叶片等热端部件的热负荷，提升对引出冷却空气的品质要求。另外，提高压气机增压比会导致引出冷却空气的冷却品质下降。针对这一矛盾，Bruening 等[1]提出了CCA(Cooled Cooling Air)技术，并表明CCA 技术将会对发动机的整体性能产生积极影响。影响CCA 技术可行性的关键因素在于换热器的研制，目前管束式换热器因其自身可靠性高、热力性能优良等优点在航空发动机上被广泛应用。

换热器的性能受其热阻影响很大，而其热阻主要分为管内对流传热热阻、管壁导热热阻和管外对流传热热阻三部分。对于航空领域常用的管束式空油换热器，其管外(即空气侧)对流传热热阻要远大于管内(即油侧)对流传热热阻和管壁导热热阻之和。因此，研究并掌握管束式换热器管外流动换热规律，进而减小管外对流传热热阻，对减小换热器总热阻具有重要意义。其中，管壁导热热阻主要涉及固体导热问题，目前已有成熟的解析解，且由于管束壁厚很薄，管壁导热热阻一般可以忽略。针对管内对流传热热阻，国内外很多学者已开展了大量的探索和研究工作并得到了诸多成果，如针对管内层流对流换热的齐德-泰特公式[2]，针对管内湍流强制对流换热的迪图斯-贝尔特(Dittus-Boelter)公式[3]，基于这些公式的计算结果已经足够准确。而相对于管内，管外的几何结构和流动特征复杂多变，很难通过解析的方法对其对流传热热阻进行计算，因此针对管束管外流动换热特性开展实验研究，获取管束管外流动换热规律，对于管外对流传热热阻的准确计算具有重要意义。

光管管束是管束式换热器的基本换热单元，其布置形式有顺排和叉排两种，换热特性主要受来流速度、管束管径、管束横向管间距比、管束纵向管间距比和流向排数等参数影响。许多学者开展了大量工作来研究上述参数对管束管外流动换热特性的影响[4]，其中Grimson[5]和Žukauskas[6]对管束管外流动换热研究的影响最广。前者较早地总结出气体横掠10 排以上管束的平均表面传热系数的实验关联式，而后者总结出的茹卡乌斯卡斯经验关系式现今仍被广泛应用于换热器设计以及管束管外换热研究[7-9]。然而，以上经典研究成果涉及到的管束管径较大，而应用于航空发动机的换热器一般为紧凑换热器，要求管束管径较小[10-12]。同时，一直从事紧凑换热器研究的Bachellar[13-14]也指出，用于验证的实验数据大部分来自19 世纪80 年代之前，相关实验所用管束管径较大。而小管径管束具有紧凑度高、对流换热系数大等优点，且目前对与管径小于5.0 mm 的管束式换热器相关的换热流阻经验关系式的研究较少，因此，对管径小于5.0 mm 的管束进行针对性研究极有必要。除实验研究，Bachellar 还采用数值方法，研究归纳出管径范围为0.5～5.0 mm 的叉排光管管束的管外换热流阻经验关系式，且与实验数据吻合较好，但缺点是公式的形式较为复杂，实用性不高。

本文探究了雷诺数、管束横向管间距比和流向管排数等变量对小管径顺排光管管束管外换热特性的影响，归纳拟合出适用于小管径的管外换热公式，为未来应用于航空航天领域的高效紧凑换热器的设计奠定了基础。

2 实验方法

2.1 实验系统

实验系统如图1 所示。空气经风机增压后通过流量调节阀，而后流经流量计测量通道，再依次进入发展段、测试段。在测试段进口，分别设置有测量来流温度、压力的T 型热电偶和压力传感器，以及测量流经实验段气流温差的温差热电偶。在测试段出口，设置有测量流经实验段气流压差的差压传感器。测试段通道中，管束壁温由红外热像测温系统测得。测试段通过导线连接至加热电源，实现对测试段通道中管束的恒电压加热，升温后的管束再对流经的空气进行加热。由于气流通过测试段后温升较小，不会对周围的实验人员或实验设备造成影响，由扩张型出口段直排大气。

图1 实验系统Fig.1 Experimental system

实验过程中，给管束施加恒定电压进行加热，空气流经升温后的管束也被加热，在保温良好的条件下，当管束温度稳定后，认为管束与空气之间的换热量等于消耗的电功，由此推导出管外对流换热系数，并最终得到管外换热努塞尔数与流动雷诺数之间的关系。相关参数定义如下：

(1) 努塞尔数(Nu)

(2) 雷诺数(Re)

(3) 管束最小截面速度(Vmax)

(4) 空气定性温度(Tf)

以上几式中：h为对流传热系数，D为管束管径，λ为空气导热系数，Q为换热功率，A为管束换热面积，Tw为管束壁温，ρ为空气密度，μ为空气动力黏度，S1/D为管束横向管间距比，Vin为来流速度，Tin为来流温度，Tout为测试段出流温度，ΔT为测试段进出口气流温差。

实验涉及到的空气物性由空气定性温度确定，然后查阅NIST(美国国家标准与技术研究院)提供的REFPROP 数据库[15]获取。

2.2 实验段

实验段主要由主体通道、可拆卸的侧面盖板、实验管束和管束底座构成，如图2 所示。主体通道由3 mm 厚的不锈钢板加工而成，其中内部空气可流通通道尺寸为54 mm×100 mm(宽×高)。装配时，先将装成一体的实验管束和管束底座从侧面置入，管束底座由通道内的卡槽和台阶进行定位与固定。之后，用侧面盖板封住通道左右两侧，通过螺栓和垫片分别进行连接和密封。侧面盖板上还安装有定制的电路板，电路板上面焊接有接线端子，用于连接通道内外电路。实验管束部分如图3、图4 所示。

图2 实验段Fig.2 Experimental section

图3 实验管束Fig.3 Experimental tube bundle

图4 实验管束截面示意图Fig.4 Section diagram of experimental tube bundle

实验过程中，固定纵向管束间距比(S2/D)，通过改变横向管束间距比(S1/D)、流向管排数(N)和流动雷诺数，探究上述参数对管束平均管外换热努塞尔数的影响规律。实验参数范围如表1 所示。

表1 实验参数Table 1 Experiment parameters

3 实验不确定度

实验所用测量仪器设备以及对应的型号和精度如表2 所示。具体的不确定计算过程所用方法见参考文献[16-17]。经过系统的不确定度计算，本实验得到的管束管外换热努塞尔数不确定度为3.4%。

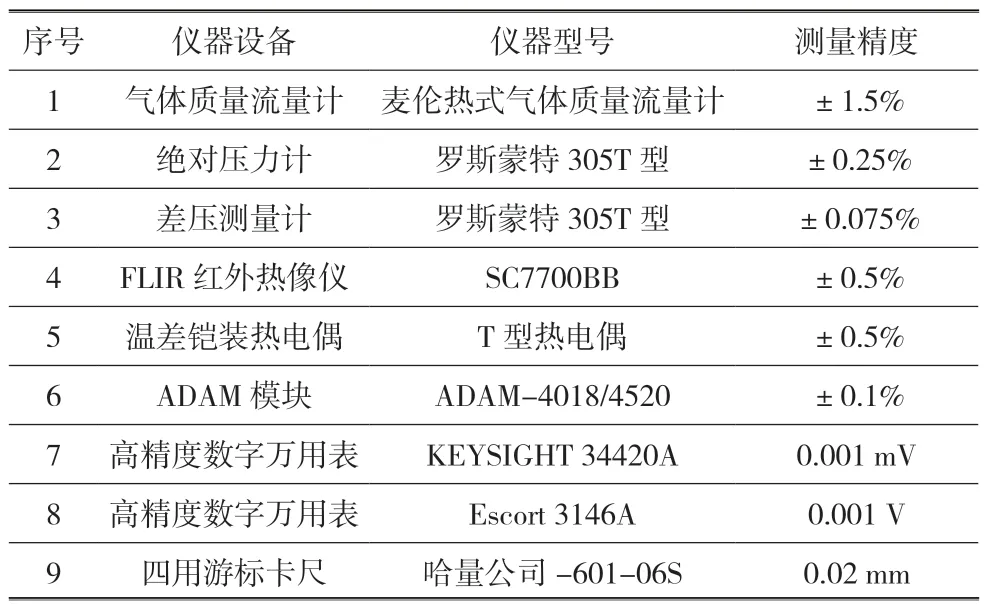
表2 测量仪器设备精度Table 2 Accuracy of measuring instruments

4 实验结果

4.1 横向管间距比对努塞尔数的影响

流向管排数为11 时，不同S1/D下管外平均换热Nu随Re的变化规律以及与常用经验关系式的对比如图5(a)所示。可以看到，不同S1/D下，随着Re的增加，顺排光管管束的管外换热Nu均随之增大，但当S1/D由3 变为2 时，Nu随Re的增长趋势有所改变。这种趋势上的变化在对数坐标下可以更直观地显示出来，如图5(b)所示。

图5 流向管排数为11 时不同横向管间距比下管外平均换热努塞尔数随雷诺数的变化Fig.5 Variation of Nu with Re at different S1/D (logarithmic scale) when N=11

茹氏经验关系式没有考虑S1/D和S2/D对Nu的影响，而当S1/D<1.5 或S2/D>2 时文献[18]中给出的经验关系式也认为管束间距比对Nu没有影响。因此，在对数坐标系下两个经验关系式的预测线斜率为定值，即形如公式(5)中指数m为定值。

在本实验中，当S1/D=3 时，换热Nu随Re增加的趋势线斜率近似为定值；而当S1/D=2 时，换热Nu随Re增加的趋势线斜率随Re的增加而减小。这表明S1/D对换热Nu存在一定的影响。其原因是，在小管径条件下，小横向管间距比意味着绝对管间距较小，流动空间小，低Re下对流动的扰动足够，紊流形成、发展较快，为此低Re下Nu随Re增加较快；而流动空间小也意味着局部流动受到了限制，在高Re下流动紊流强度的进一步增强受到限制，高Re下Nu随Re增加的速率减慢。

预测精度方面，茹氏公式预测值较实验结果偏大，平均偏差6.3%，最大偏差11.0%；文献[18]中给出的经验关系式的预测值较实验结果偏小，平均偏差-6.4%，最大偏差-10.5%。可以看到，流动Re在1 500～6 000 范围内时，常用的换热经验关系式的预测精度基本在10%的相对误差范围内。

4.2 流向管排数对换热努塞尔数的影响

不同流向管排数下管束平均管外换热Nu随流动Re的变化规律如图6 所示。可以看到，S1/D=3 和S1/D=2下，换热Nu均随着流向管排数的增加而增加，且逐渐趋于定值。这是因为随着管排数的增加，相对稳定的来流经过管束的扰动，逐渐发展成脉动强度较大的湍流，对管束换热起到强化作用，因此Nu迅速增大；经过多排管束后，流动得到充分发展并趋于稳定，流体与管束之间的换热也进入稳定状态，因此随着管排数的进一步增加，Nu增大的幅度越来越小并趋于稳定值。图中10 排和11 排的管束平均换热Nu曲线几乎重合，这说明管排数增加到10 排左右管束流动换热就已经得到充分发展。

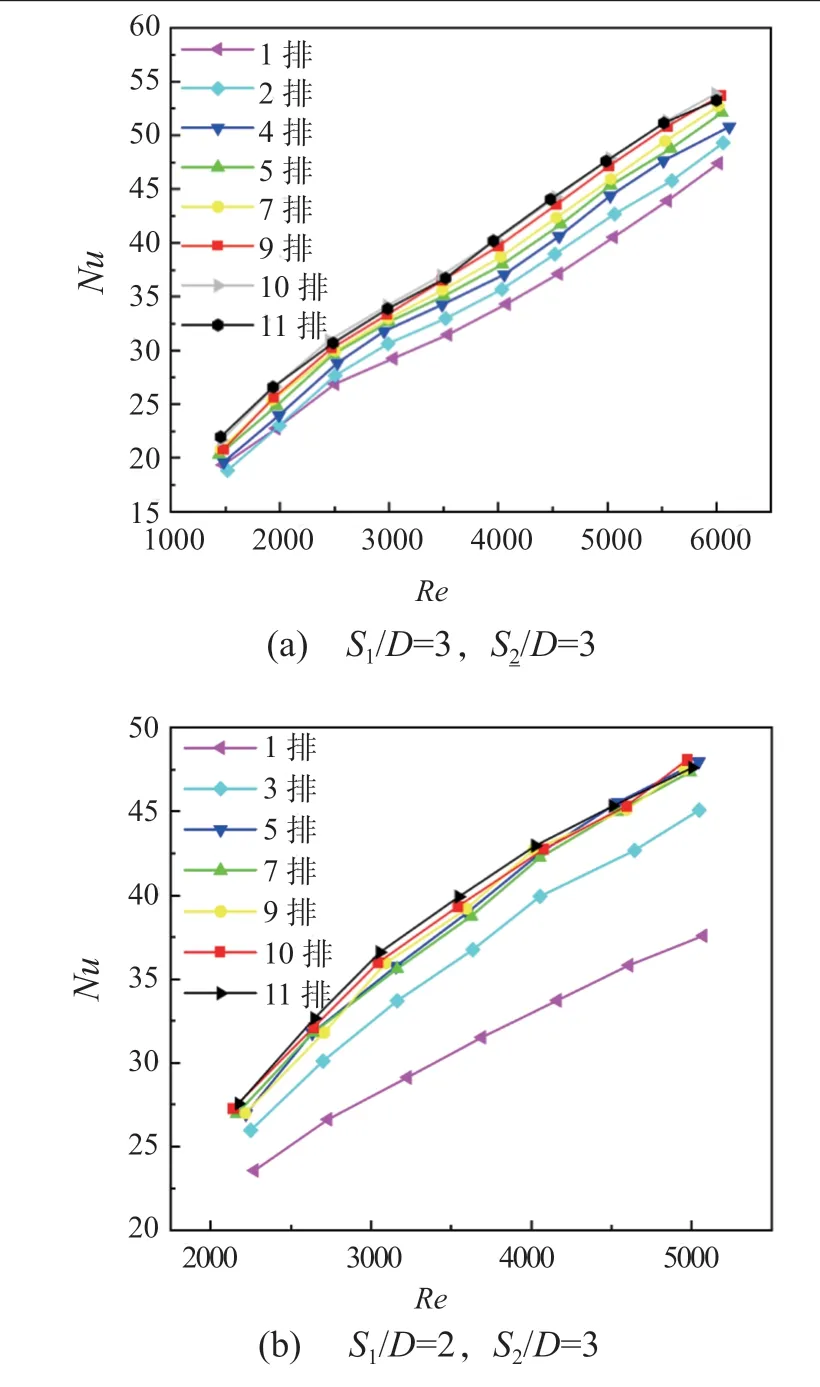
图6 不同管排数下管束平均管外换热努塞尔数随雷诺数的变化Fig.6 Variation of Nu with Re at different tube row numbers

值得注意的是，不同S1/D下流动在管束间的发展过程并不相同。S1/D=3 时，管排数增加至7 排时Nu就不再明显增大；而S1/D=2 时，管排数增加至5 排时Nu就不再明显增大。这说明横向间距比越小，流体被扰动得越快，紊流越先发展至充分状态。

特别地，流向管排数只有1 排时管束换热Nu最小，这是因为来流没有经过管排的扰动，流体脉动强度较弱，与管束的换热较弱，形式上类似于横掠单管的流动换热。图7 给出了单排管束换热Nu实验结果与经验关系式的比较，可见两者结果相近。

图7 单排管束换热努塞尔数实验结果与经验关系式对比Fig.7 Comparison of experimental Nu with prediction by empirical correlation when tube row number N=1

4.3 小管径顺排管束管外努塞尔数关系式拟合

为方便小管径管束式换热器设计，可将上述实验数据拟合为形如公式(6)所示的Nu-Re经验关系式。由于研究范围限于空气且温度变化不大，因此公式拟合中忽略了物性变化带来的影响，不引入普朗特数项。公式拟合数据为流动充分发展的11 排管束数据，1～10排的管束换热Nu通过管排修正系数来确定。最终拟合所得小管径顺排光管管束管外换热Nu经验关系式如公式(6)所示。图8 为拟合结果、实验数据和经验关系式的对比，可见拟合效果较好，拟合关系式结果介于茹氏公式和文献[18]所给公式之间。

图8 努塞尔数拟合关系式及其与实验数据和常用关系式的对比Fig.8 Nu fitting formula and its comparison with experimental data and empirical correlation

5 结论

通过对管直径为2 mm 的小管径顺排光管管束进行换热特性实验研究，探究了换热努塞尔数与横向管间距比、流向管排数和流动雷诺数的关系规律，主要得到以下结论：

(1) 茹氏公式等经典换热经验关系式对小管径管束管外换热努塞尔数的预测偏差基本上在10%以内，属于可接受的误差范围。

(2) 管束的横向管间距比影响管外努塞尔数随雷诺数的增长速率。横向管间距比等于3 时，努塞尔数随雷诺数增长平稳；横向管间距比等于2 时，努塞尔数随雷诺数增长速率先快后慢。

(3) 管束的平均管外换热努塞尔数随流向管排数的增加而增大，且这种趋势在小横向管间距比时更为明显。综合来看，努塞尔数在管排数大于10排时趋于稳定值。