直接加温条件下燃烧室燃烧效率计算方法研究

张 杰，王 军，蒙正猛，姜明宏，邓胜军，宋 平

(1.中国航发四川燃气涡轮研究院，四川 绵阳 621010；2.四川大学 a.化工学院；b.空天动力燃烧与冷却教育部工程研究中心，成都 610065)

符号表

hi燃气成分的摩尔比焓，i=H、O、N、N2、CO、O2、H2O、CO2、Ar、UHC、NO、NO2、OH、H2

Hf2燃烧室燃料的绝对燃烧焓

Mf2燃烧室燃料的摩尔质量

p燃烧室内压力

Tf1直接加温器燃料温度

Tf2燃烧室燃料温度

Tg1直接加温器出口温度(燃气分析法)

Tg2燃烧室出口温度(燃气分析法)

Wa1直接加温器的空气质量流量

Wf1直接加温器的燃料质量流量

Wf2燃烧室的燃料质量流量

x未燃碳氢化合物中碳原子数

y未燃碳氢化合物中氧原子数

α直接加温器和燃烧室总余气系数(流量法)

α1直接加温器余气系数(流量法)

α2燃烧室余气系数(流量法)

αT直接加温器和燃烧室总余气系数(燃气分析法)

αT1直接加温器余气系数(燃气分析法)

αT2燃烧室余气系数(燃气分析法)

η1直接加温器燃烧效率(燃气分析法)

η2燃烧室燃烧效率(燃气分析法)

φi直接加温器出口燃气各成分的体积分数，i=N2、CO、O2、H2O、CO2、Ar、UHC、NO、NO2

1 引言

随着航空发动机推重比的提高，燃烧室出口燃气温度越来越高。特别是先进战斗机发动机的燃烧室出口热点温度，已超过热电偶的测量极限。当燃气温度较高时，水冷热电偶测温的换热和辐射误差较大。为此，需要寻求其他方法来测量燃烧室出口高温燃气温度[1-2]。随着燃气分析技术的发展、工程实践应用的深入和燃气分析仪器配置(CO2、CO、NOx、UHC(未燃碳氢化合物，分子式用CxHy表示)、O2、H2O 等分析仪)的完备，目前国内外研究机构已具备采用全成分分析法推演余气系数、燃烧效率和燃气温度的条件[3]，燃气分析技术已成为高温燃气测试及计算不可或缺的手段。

燃烧室全成分分析法已成熟应用于多型燃烧室性能评估[4-7]，但该方法仅适用于间接加温(电或天然气加温器等)的纯净空气燃烧模型。受加温设备功率和燃烧室进口温度等因素的限制，进口空气直接加温的方式能够突破加温能力的限制，但燃烧过程存在不完全燃烧，燃烧产物会影响燃烧效率的准确性。基于上述原因，沿用燃烧室全成分法将导致计算的带直接加温器的燃烧室燃烧效率存在较大偏差，影响试验结果评判，但全成分分析法的计算思路，仍然适用于带直接加温器的燃烧室燃烧效率的评估。

为了满足带直接加温器的燃烧室燃烧效率的测试需求，本文根据带直接加温器的燃烧室的工作原理建立了数学模型，利用全成分分析法的理论，推导了直接加温的燃烧室燃烧效率的算法，描述了全成分分析法的数学模型、基本假设和推导过程。

2 燃气分析系统

燃气分析法是通过取样探针测量具有代表性的燃烧室出口燃气成分，利用全成分分析法和焓值守恒法，推算油气比、燃烧效率、燃气温度和排放指数等参数的一种方法。燃气分析系统由取样探针、预处理系统、分析仪器和测控系统等组成。其中，气体分析仪器用于测量UHC、CO、CO2、NOx浓度——UHC 采用火焰离子检测器原理测量，CO、CO2采用非分光红外原理测量，NOx采用化学发光法原理测量[8]。

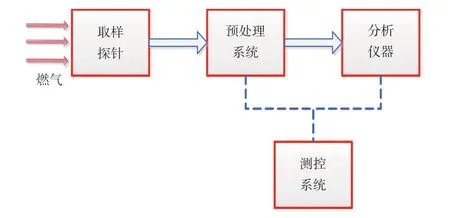
图1 燃气分析系统原理图Fig.1 Schematic diagram of gas analysis system

3 数学模型与基本假设

3.1 数学模型

带直接加温器的燃烧室数学模型如图2 所示。试验系统包括直接加温器和燃烧室两个燃烧系统。直接加温器和燃烧室既可采用相同类型的燃料(如RP3)，也可采用不同类型的燃料(如直接加温器采用酒精、燃烧室采用RP3)。

图2 带直接加温器的燃烧室数学模型Fig.2 Mathematical model of combustor with direct heater

针对带直接加温器的燃烧室的工作特性，在直接加温器和燃烧室出口位置分别测量其燃气成分，其计算思路如下：

(1) 直接加温器工作、燃烧室不工作时，测量直接加温器出口截面燃气成分(UHC、CO、NO、NO2、CO2)的体积分数，推算燃烧室进口截面各成分的体积分数；

(2) 将燃烧室进口成分视为燃烧室反应过程的氧化剂，在燃烧室稳定工作过程中，对燃烧室出口截面进行燃气取样，测量燃烧室出口截面燃气成分(UHC、CO、NO、NO2、CO2)的体积分数；

(3) 根据燃烧室进、出口截面的燃气成分，计算直接加温进气条件下燃烧室的燃烧效率。

确定各成分的含量时，部分来自在线测量，部分来自计算。目前，根据燃气分析仪器的发展和在常规燃烧室性能试验中的使用情况，能在线测量的成分通常有CO2、CO、NO、NO2、UHC 等，其他的成分含量需通过计算确定，计算依据的基础是反应中的质量守恒定律。

3.2 基本假设

(1) 直接加温器采用液态碳氢燃料燃烧时，假设其通用分子式为CmlHnlOllNkl(m1、n1、l1、k1 分别为1 个直接加温器燃料分子中C，H，O，N 原子的个数)；燃烧室采用液态碳氢燃料燃烧时，假设其通用化学分子式为Cm2Hn2Ol2Nk2(m2、n2、l2、k2 分别为1 个燃烧室燃料分子中C，H，O，N 原子的个数)[9]。

(2) 忽略燃烧室出口高温燃气中的C 和N。

(3) 燃烧室进口截面温度低于1 650 K，假设燃料和氧化剂之间反应可认为是单步不可逆反应，燃气成分不考虑热离解，含有N2、CO2、Ar、H2O、O2、NO、NO2、CO、UHC 共9 种成分。

(4) 燃烧室出口截面温度高于1 650 K，假设燃料和氧化剂之间反应可能存在单步可逆反应，燃气成分应考虑热解离效应，包括CO2、CO、UHC、H2O、NO、NO2、Ar、O2、N2、O、H2、H、OH 共13 种成分。

(5) 分别测量直接加温器出口截面和燃烧室出口截面的CO2、NO、NO2、CO、UHC 等成分，其余成分采用质量守恒方程和化学平衡方程导出。

(6) 假设直接加温器和燃烧室组成的燃烧系统在燃烧过程中散热损失小，2 个燃烧系统均为定压绝热燃烧系统。

(7) 已知燃料的成分、温度、低热值和燃烧空气的温度、压力、含湿量，或同时被测量。

4 计算过程

4.1 直接加温器反应过程

已知干空气中N2、O2、CO2和Ar 的体积浓度分别为A=0.780 881，B=0.209 495，C=0.000 3，D=0.009 324，空气中H2O 的摩尔含湿量d=0.018，直接加温器出口截面燃气成分测量值φi(i=UHC、CO、CO2、NO、NO2)。以1 mol 燃料为计算基础，在空气实际燃烧的试验条件下，燃料与空气在直接加温器中不完全燃烧反应的关系式为：

式中：P0为空气的摩尔数，P1～P9分别为1 mol直接加温器燃料燃烧对应生成物N2、O2、CO2、CO、UHC、H2O、NO、NO2、Ar 的摩尔数(Pi)。

根据C、H、O、N、Ar 元素守恒和直接加温器出口截面燃气成分测量值，共有生成物总摩尔数Pg、P0～P9、φ(O2) 共12 个未知数，由此可以求解出1 mol 燃料参与直接加温器反应过程所消耗的P0、Pg、P1～P9和φ(O2)。

4.2 燃烧室进口截面参数

根据4.1 节计算结果，在直接加温器燃烧过程中，1 mol 燃料不完全燃烧，得到反应后总摩尔数和9 种生成物摩尔数，两者相比可得9 种生成物体积分数，即燃烧室进口截面氧化剂的体积分数。

已知直接加温器反应后总摩尔数、9 种生成物摩 尔 数，令A2、B2、C2、D2、E2、F2、G2、J2、R2分别为1 mol 燃烧室反应物蕴含N2、O2、CO2、CO、UHC、H2O、NO、NO2、Ar 的体积分数，则：

4.3 燃烧室化学反应过程

根据4.2 节得到的燃烧室进口的氧化剂，采用考虑燃烧室中热解离效应的模型，燃烧室供应的燃料为碳氢燃料。已知燃烧室进口的氧化剂体积分数，燃烧室出口测量值(φ(UHC)*、φ(CO)*、φ(CO2)*φ(NO)*、φ(NO2)*)，则1 mol 碳氢燃料与燃烧室进口的氧化剂燃烧的化学反应方程式为：

式中：P0*为燃烧室进口氧化剂的摩尔数，P1*～P13*分别为1 mol 燃烧室燃料燃烧对应生成物CO2、CO、H2O、N2、O2、UHC、NO、NO2、Ar、O、H、OH、H2的摩尔数(Pi*)。

根据C、H、O、N、Ar 元素守恒和燃烧室出口截面燃气成分测量值，共6 个方程，无法求解出11 个未知数，故需考虑H2O、H2、O2三种成分的热离解反应。

根据水的解离反应2H2O=2H2+O2有：

根据水的解离反应H2O=H+OH 有：

根据H2的解离反应H2=H+H 有：

根据O2的解离反应O2=O+O 有：

Kp只决定于该化学反应进行的温度，可按(-E/RTg2) 确定。其中，A和n为反应决定的系数；E为活化能，单位为J/mol。

根据热力学第一定律，燃烧反应前后物质的绝对焓相等，即

式中：上标2 表示燃烧室进口反应物所处状态。由于KPi、Hi只与燃烧室出口温度有关，因而求解上述11 个方程，共有11 个未知数，可得到唯一的解。

由于(12)～(15)的解离方程是Tg2的函数，而为非线性函数，引入解离方程后，方程组变成非线性方程组，Tg2本身成为未知数，需将非线性方程组转化为线性方程组求解。三变量迭代法是基于范作民提出的双变量迭代法(N2和O2)的基础上增加一个T作为迭代变量参与计算，该方法的优点是算法编程简单，计算速度快且收敛性很好。

在三变量迭代法中，首先设定燃气温度、燃气中氧气浓度、氮气浓度的初值，根据燃气温度可得到各化学平衡常数；然后利用化学平衡方程，依次求解得到各成分浓度，根据式(16)可得到燃气温度。如此反复迭代，即可获得方程组的解。

为了加快迭代计算的收敛速度，以不考虑离解时计算得到的N2、O2、CO2、H2O、CO、NO、NO2、Ar、UHC 的浓度和、、Tg2作为上述各量的初值，H2、H、OH、O 等成分浓度的初值取10-10，作为方程组的近似解。

4.4 燃烧效率计算

4.4.1 余气系数计算

燃烧室组织燃烧时，实际消耗的氧化剂流量与供入的燃料理论完全燃烧所消耗的氧化剂流量的比值称为余气系数。由于燃烧室进口的氧化剂中含有UHC 和CO，这两种成分在组织燃烧过程中会消耗氧化剂中的氧气，故计算余气系数时应扣除氧化剂中UHC 和CO 所消耗的氧气量，不然会导致余气系数偏大。余气系数的计算式为：

4.4.2 燃烧效率计算

燃烧室组织燃烧时，燃料燃烧后实际放出的热量和燃料完全燃烧后放出的热量的比值称为燃烧效率。设燃烧室供给的燃油热量和氧化剂中UHC、CO 所蕴含的热量为反应前总的热量，为Q1，燃烧室出口高温燃气中不完全反应生成的CO、UHC、H2、OH、O、H 所蕴含的热量为Q2，有

则燃烧室燃烧效率计算公式为：

式中：Qi为已知摩尔反应的焓变，单位为J/mol。

5 应用实例

在某带直接加温器的燃烧室试验中，分别在直接加温器出口、燃烧室出口安装取样探针，利用燃气分析系统[10]，测量直接加温器出口和燃烧室出口样气成分，并计算带直接加温器的燃烧室的燃烧效率。

5.1 直接加温器试验结果

对直接加温器出口燃气进行取样和分析，直接加温器出口截面UHC、CO2、CO、NO、NO2体积浓度的测量与计算结果如表1 所示。

表1 直接加温器出口截面浓度测量与计算结果Table 1 Concentration measurement and calculation results in outlet section of direct heater

根据SAE RP1533B[11]规定，在慢车(小功率)状态下余气系数的偏差在15.0%以内，在大功率状态下余气系数的偏差在10.0%以内，效验计算方法的数据有效性。直接加温器流量法的余气系数分布在3.83～3.85，燃气分析法的余气系数分布在3.73～3.78，偏差最大值为1.8%，远小于10.0%，说明燃气取样结果合理。同时，直接加温器的燃烧效率约为0.996 5，表明直接加温器在该状态下燃烧稳定。取表中测量结果的平均值，可计算得到燃烧室进口截面的氧化剂组成。

5.2 燃烧室试验结果

5.2.1 燃烧室测试结果

保持直接加温器试验工况不变，在燃烧室出口对5 个不同试验工况进行燃气取样，获取燃烧室出口成分。燃烧室出口成分测量结果如表2 所示。直接加温器和燃烧室总燃烧系统的余气系数(流量法)分布在1.14～2.56，燃气分析法的余气系数分布在1.19～2.60，偏差分布在1.4%～4.2%，远小于10.0%，说明燃气取样结果具有代表性。

表2 燃烧室出口截面测量与计算结果Table 2 Concentration measurement and calculation results in outlet section of combustor

5.2.2 燃烧室计算结果

基于VB 高级语言，对第3 节的计算方法进行编译，计算软件的计算结果如图3 所示。利用5.1节直接加温器试验数据和5.2.1 节燃烧室出口测量数据，通过计算软件，计算得到如表3 所示的燃烧室出口截面参数。表中，为基于总温探针的燃烧室出口温度测试结果。

表3 燃烧室出口截面计算结果Table 3 Calculation results of outlet section of combustor

图3 计算软件的计算结果Fig.3 Results of calculation software

由表3 可知，随着余气系数的减小，燃烧效率先增加后减小，表明该燃烧室存在最佳的燃油组织方式。当余气系数小于2.8 时，燃烧室内O2消耗增加，导致CO2生成的同时CO 的量迅速增加，燃烧效率随之下降。另外，随着余气系数的减小，燃烧室出口温度增加。当燃烧室出口温度小于2 100 K 时，热电偶所测温度高于燃气分析法所计算温度，其原因在于燃气分析法扣除了燃烧室出口UHC 和CO 等未完全反应物所蕴含的热量，以及同时考虑了高温热离解反应所吸收的热量。

6 结论

以主燃烧室全成分法为基础，结合带直接加温器和燃烧室的工作原理和物理模型，建立了数学模型，利用全成分分析法的基础理论，推导了直接加温进气条件下燃烧室燃烧效率的计算方法，并进行了实例验证。该算法有效继承和拓宽了主燃烧室全成分法，并通过在直接加温器出口和燃烧室出口上进行取样试验，证明了计算方法的合理性。该算法可用于带直接加温器或非纯净高温加热的主燃烧室或涡轮模态的超级燃烧室的燃烧效率计算，拓宽了燃气分析技术的工程应用领域。