一道导数零点差试题的命制历程
2024-01-09卢依婷董泉发
卢依婷, 董泉发
(杭州第二中学钱江学校,浙江 杭州 311215)
函数是高中数学阶段的一个重要内容,我们常用导数研究其单调性、极值点、最值等问题.函数的零点问题是高考的热点之一.其中,在有明显凹凸变化趋势的一些超越函数中衍生出了一类试题——零点差问题.
下面笔者展示浙江省杭州第二中学学术节命题比赛中命制的一系列函数与导数试题及其探究历程.
1 试题与分析



(提示:e-0.2≈0.818 73.)
此题主要考查导数的计算、应用、几何意义,以及利用导数探讨函数单调区间和极值的方法,考查灵活应用导数工具分析、解决零点之间的相互关系的迁移能力,考查利用切线或曲线放缩对问题进行简化的化归与转化思想,考查数学运算、逻辑推理、直观想象等核心素养,体现了综合性、应用性与创新性.
函数g(x)的图象如图1所示,由
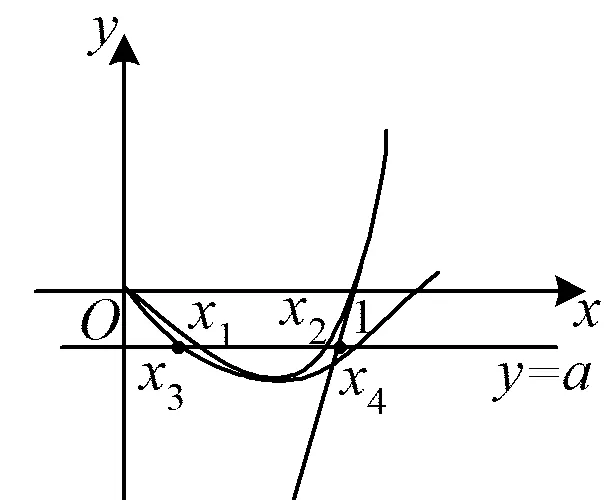
图1
知,可通过二次曲线缩小左侧零点x1、切线放大右侧零点x2得到新零点x3,x4.




下证x4>x2.令h(x)=g(x)-m(x),则


即
g(x)>m(x),
故
g(x2)>m(x2).
又
g(x2)=m(x4),
则
m(x4)>m(x2),
由m(x)单调递增可知x4>x2.

其与y=a的交点横坐标记为
同理构造函数t(x)=g(x)-n(x),则
t′(x)=g′(x)-n′(x)
由t‴(x)在(0,1)上恒大于0,知t″(x)在(0,1)上单调递增,且
从而t″(x)在(0,1)上存在唯一零点x0,且x0∈(0.5,0.8),满足

又函数y=ex0-1(4x0+1)+2x0在(0.5,0.8)上单调递增,可知
故t′(x)有正有负,令t′(a1)=0(其中0.5 t(1)=t(0)=0, 故在区间(0,1)上,t(x)>0.即 g(x)>n(x), 故 g(x1)>n(x1). 又 g(x1)=n(x3), 则 n(x1)>n(x3), 由n(x)在(0,1)上单调递减可知x1>x3. 在上述试题的命题过程中,笔者经历了“构思—模仿—创新”的心路历程,目标明确,过程曲折,终得定稿. 一方面,源于教材.在人教A版《普通高中教科书·数学》(以下统称“教材”)(选修第二册)“导数的概念及其几何意义”中,提到切线的其中一个应用“以直代曲”.此外,在教材“导数的运算”一节的探究与发现中,拓展了牛顿法求解方程的近似解.实际上,估计零点距离的本质就是用简单的函数拟合复杂的函数对象,将难以求出的零点可视化. 另一方面,源于实际.近期,数次联考(如宁波市九校高三联考、三湘名校高三联考等)都考查了零点差.2023年3月,萧山中学开展的学术节也选取了该内容作为交流主题.该内容有较强的综合性,且有较大的可塑性,适合作为考点. 在试题命制的过程中,笔者主要考虑两个问题:如何选择函数,以及如何设置问题. 2.2.1 构造函数 在函数的选择方面,需借助几何画板软件构造函数,追求函数结构的简洁美,且具有明显的凹凸性.首先,从零点差问题中常见的幂函数、对数函数、指数函数这3类入手.虽然从图象上看,3类函数的凹凸性很明显,但是选择用幂函数和指数型函数构造,能够降低在代数运算上的困难.其次,笔者设想构造的函数零点最简化,即为0,1.零点需幂函数部分控制,即(x2-x),因此初次构造的函数为g(x)=ex+1(x2-x).但在研究这个函数的过程中,发现极值点带根号,于是再次尝试优化函数的形态. 为得到零点和极值点双美的函数,笔者化零点两定为一定一动,将幂函数部分改成一般函数ax2+bx,同时将g(x)变成eax+b(ax2+bx),其导函数为 eax+b[ax2+(2a+b)x+b]. 由于只关注(0,+∞)上的极值点,因此只需满足 2.2.2 设置问题 文献[1]提出,命题可从提问方式、题设条件、综合程度上调整难度. 设置的问题需入口宽,能控制平均分在4分左右(满分12分),即大多数学生可得到基础分;设置的问题须有梯度,能选拔人才,即所提的问题是递进的,彼此间存在层次上的联系;此外,须紧扣数学核心素养,综合考查多种数学思想、方法和数学能力. 第1)小题分析:根据以上命题原则,就函数的图象特征可提出关于单调性、极值、零点、切线的问题,如①讨论函数g(x)的单调区间;②讨论函数g(x)的极值;③若函数g(x)=m有两个解,求m的取值范围;④求函数g(x)在x0处的切线方程.上述问题均可作为试题的第1)小题,不仅考查了利用导数研究函数单调性、极值,而且可为第2)小题研究函数的零点差做铺垫. 第2)小题分析:考查目标明确,零点差问题有切线、割线、二次曲线放缩3种模式.实际上,该类问题的解答步骤是程序化的:第1步,在得到使得函数与直线有两个零点的参数范围后,观察函数的单调性和凹凸性;第2步,判断用切割线方程或者二次曲线方程放缩;第3步,构造函数并根据其单调性判断出切割线或二次曲线与函数之间的位置关系;第4步,将函数的零点放缩为切割线或二次曲线对应的零点[2]. 目前,该类命题通常选择某一种模式放缩两边零点(见图2~4),弊端是学生容易形成思维定式,按部就班.笔者思考:能否反套路,采用不同放缩形式估计零点差,但又不那么刻意. 图2 图5 基于该命题思路,笔者改变了目标结构和提问方式得到2个变式. 方向1“零点差”→“零点商”. 变式1已知函数g(x)=ex+1(x2-x). 1)讨论g(x)的单调区间; 将零点差问题变成零点商问题,难度更上一层楼.若学生有较强的迁移能力,则能够发现零点商的本质也是零点的放缩,拨开云雾见月明.既可以直接将零点x2放大,x1缩小,也可以将两边取对数化成 化归为零点差的问题. 方向2“零点差”→“零点和”. 此处,笔者借鉴了2021年全国数学新高考Ⅰ卷函数压轴题的命题思路,看似是零点和,考查极值点偏移,实际上右侧不等式也可用切割线放缩处理. 例2已知函数f(x)=x(1-lnx). 1)讨论f(x)的单调性; (2021年全国数学新高考Ⅰ卷第22题) 方向3造台阶. (提示:e-0.2≈0.818 73.) 原题难度较大,若增设一问,证明二次函数处于曲线下方,则能够给学生搭建台阶,提醒学生可向二次曲线放缩方面思考,从而降低思维难度. 命题不仅要追求题目的简洁美,还要尽可能保证关键要素的简洁美,目标函数可以在考点确定后再调整.成熟的考点未必没有创新之处可开发,突破思维定式、拒绝套路有利于学生思维的发展.在教学时,我们要重视学生基本的运算能力和概念的掌握,多引导学生亲身经历一类问题的解决过程,渗透问题解决时所用的思想方法与本质,必要时可借助几何画板软件等工具进行辅助,同时也要善于总结和反思,提高效率.
2 设想与命题
2.1 命题溯源
2.2 命题思路

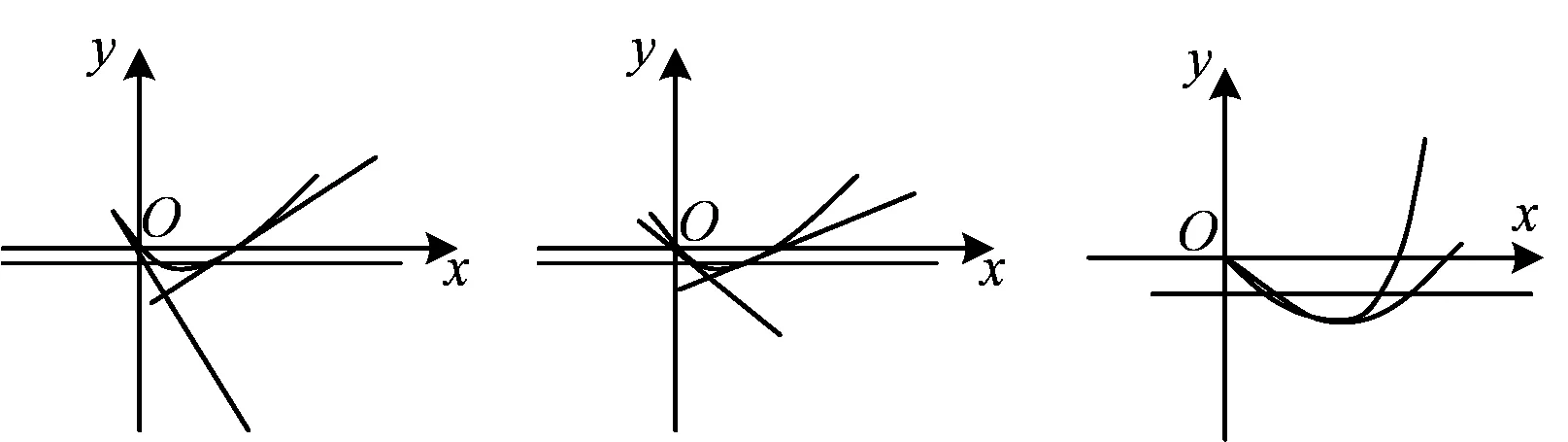

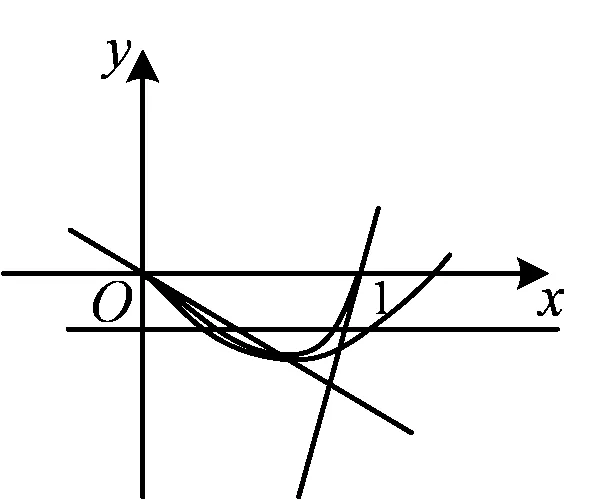
2.3 命题反思






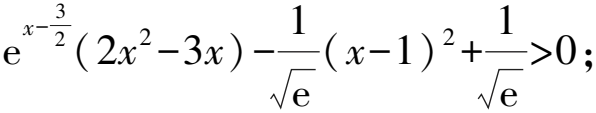

3 命题感悟
