基于主成分分析和深度森林算法的S700K转辙机故障诊断

胡小晨， 郭 宁， 沈 拓， 董德存

（1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804）

在铁路第六次提速和道岔系统日益复杂的情况下，S700K 转辙机作为铁路信号的重要设备面临严峻的挑战。目前，转辙机的故障诊断主要通过人工观察微机监测系统所采集的电流或功率曲线实现，现场人员必须具备全面分析信息的能力和快速维护的经验。因此，对转辙机的智能化诊断显得尤为重要。

国内外学者对转辙机故障诊断方法进行了大量的研究。黄世泽等［1］采用费雷歇距离定义的相似函数进行故障诊断。许庆阳等［2］采用Fisher 准则函数和主成分分析（PCA）进行特征提取，通过建立不同故障分类下的隐马尔科夫模型（HMM）进行故障诊断。孔令刚等［3］通过概率神经网络（PNN）提取功率曲线多域特征数据实现故障诊断。Ou等［4］采用主成分分析和线性判别分析进行特征约简，并使用支持向量机（SVM）对故障进行分类。池毅等［5］将一维卷积神经网络应用于转辙机故障诊断。王瑞峰等［6］将灰色关联理论与神经网络相结合，实现转辙机故障识别。Ou 等［7］基于不平衡监测数据，提出了一种基于贝叶斯估计的道岔在线故障诊断方法，在高准确率的前提下减少了训练时间。赵盼等［8］采用贝叶斯元学习方法，无须额外扩充小样本数据集，实现对多种型号的转辙机故障诊断。

作为机器学习方法，集成学习的主要思想是通过特定的规则整合各种学习结果，从而获得比单一学习者更好的学习性能。在综合学习和深度学习的基础上，Zhou 等［9］提出了深度森林（gcForest）模型，并将其引入级联框架，生成具有更丰富学习能力的深度森林模型。目前深度森林算法已经广泛用于图像处理、时间序列预测等领域。Liu等［10］将深度森林算法应用于水轮机故障诊断。结果表明，此方法的诊断精度优于现有方法，对噪声具有较好的鲁棒性，并且不受训练数据量的限制。Qin 等［11］将XGBoost（extreme gradient boosting）和 LightGBM（light gradient boosting machine）替代级联森林的原有分类器，对滚动轴承进行故障诊断。结果表明，该方法能准确识别出不同类型故障，同时具有非常少的超参数和非常低的计算机硬件要求。Zhang 等［12］采用改进深度森林算法和案件推理对ZYJ7 道岔进行故障诊断。由于一些故障集具有相似的特征，因此基于案件推理能更好地区分故障。实验结果表明，在数据有限时精度优于现有方法。

采用主成分分析对S700K转辙机的三段电流曲线进行特征提取，然后将简约特征嵌入功率曲线深度森林模型中进行故障诊断。经过现场实际数据验证，该方法可有效提高故障诊断的精度与效率。

1 S700K转辙机动作过程分析

S700K转辙机是高速铁路和提速段常用的交流式转辙机。不同类型转辙机的输出功率规律相似，S700K转辙机具有一定的代表性。

1.1 S700K转辙机正常工作状态

S700K 转辙机正常运行时的电流、功率曲线如图1所示。S700K转辙机运行包括3个阶段，依次为启动、转换、指示。第一阶段是开关机启动，道岔开锁需要克服较大阻力；第二阶段是开关轨道移动到另一个基本轨道的过程以及道岔锁紧；第三阶段是使用低功耗指示电路指示转换。

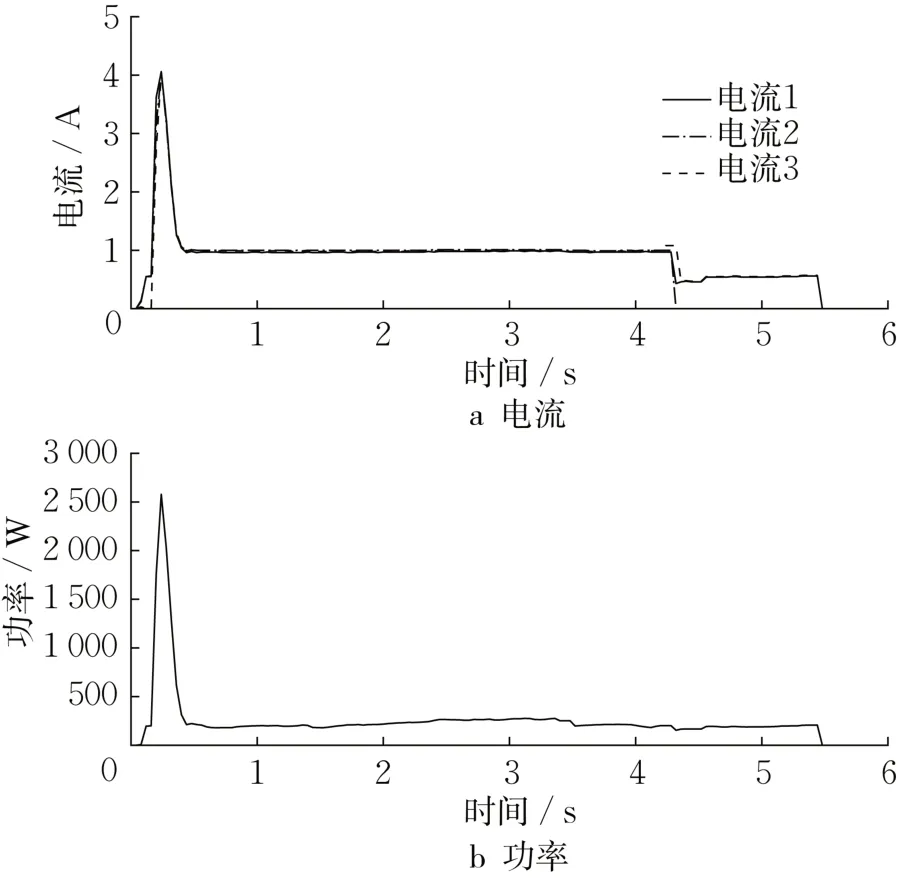
图1 S700K转辙机正常运行时的电流、功率曲线Fig.1 Normal current and power curves of S700K switch machine

1.2 S700K转辙机故障工作状态

S700K转辙机具有复杂的机电结构，长时间暴露在户外环境中并需要频繁拉动，根据前期研究［13］再结合现场数据，S700K转辙机的常见故障如表1所示。

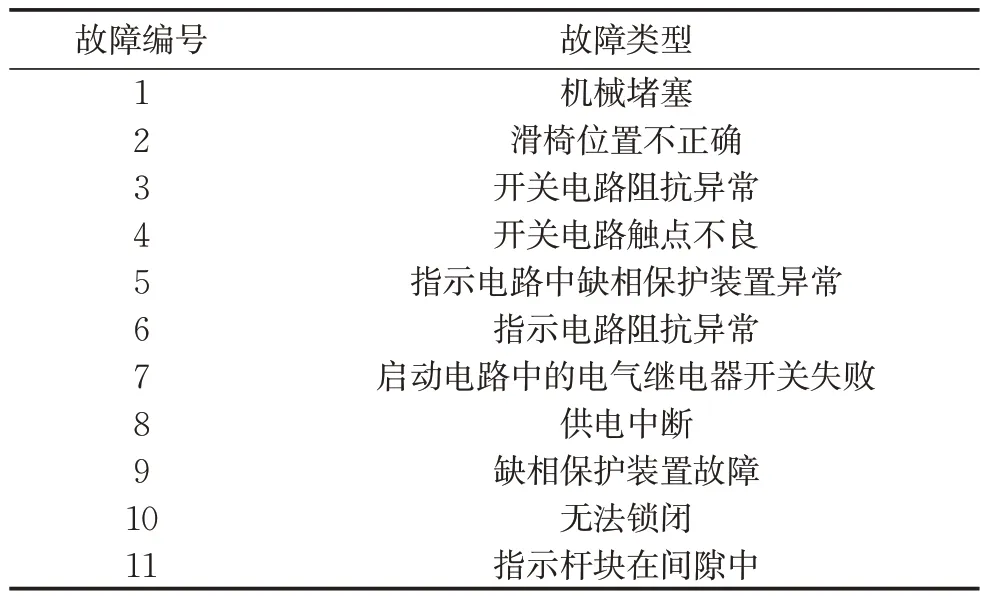
表1 S700K转辙机故障类型Tab.1 S700K switch machine fault types

2 基于主成分分析的特征参数提取

主成分分析［14］是一种常见的数据分析方法，常用于高维数据的降维，以提取数据的主要特征分量。该方法在信号处理、模式识别、数字图像处理、故障诊断等领域已经得到了广泛应用。

主成分分析通过线性转换将现有特征转化为新特征。新特征根据数据集的方差进行排序，这意味着具有最高表示能力的特征被选择用于分类。

假设矩阵X中包含m个样本和n维特征，则主成分分析基本步骤如下：

第1 步将X中心化，即分别求出每个特征的平均值，计算式如下所示：

式中：μi为第i维特征在m个样本上的平均值；xji为第j个样本的第i维特征值。对于所有的样例都减去对应的均值，得到中心化后的矩阵X0，计算式如下所示：

第2步计算中心化后的矩阵X0的协方差矩阵

第3 步用奇异值分解（SVD）求出协方差矩阵的特征值及其对应的特征向量，如下所示：

式中：U是一个m×n的方阵，由于内部向量是正交的，因此又称为左奇异矩阵；Σ是一个m×n的实对角矩阵，由于对角线上的元素为奇异值，因此又称为奇异值矩阵，；V是一个n×n的矩阵，由于内部向量也是正交的，因此又称为右奇异矩阵。

第4步将特征值从大到小排序，选择其中最大的kp个，然后将其对应的特征向量分别作为行向量组成特征向量矩阵Xe。

第5 步将原始数据转换到kp个特征向量构建的新空间中，经主成分分析处理后得到具有kp维特征的矩阵Xnew，表达式如下所示：

在上述原理下，绘制降维后各成分的方差和随主成分个数的变化而变化的曲线，选取最优主成分个数。原始数据包含360 维特征，计算不同降维维度kp下的投影误差，得到如图2 所示的曲线。可以看出，当方差和约为95%时，即降维后的特征值保留了原始特征值95%的信息，kp的取值约为10，这样就完成了特征数据的最优主成分个数选取。

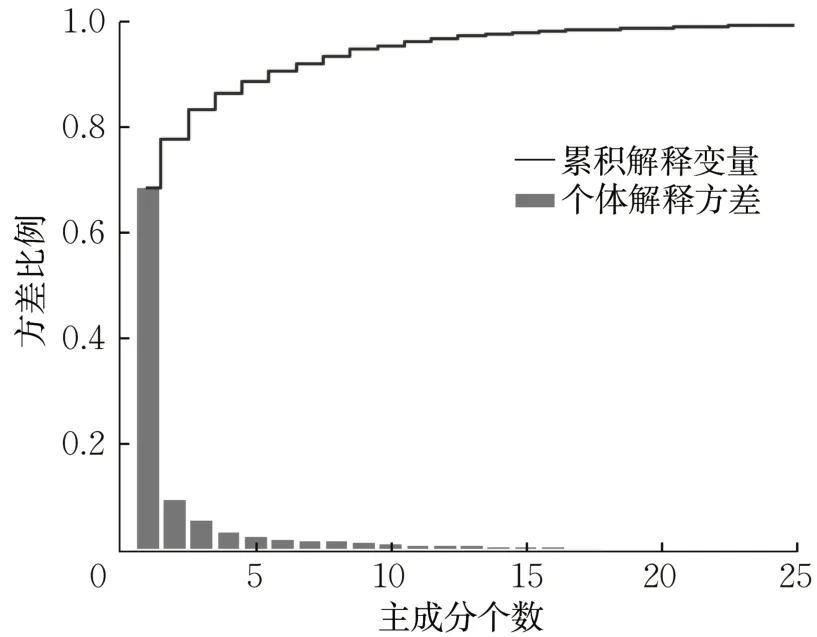
图2 主成分分析的最优主成分个数Fig.2 Number of PCA optimal principal components

3 基于主成分分析的改进深度森林算法

3.1 多粒度扫描

多粒度扫描过程中采用不同大小的滑动窗口对原始输入特征进行提取，可以产生多个不同维度的特征，从而增强样本多样性。与原始输入特征相对应的特征实例经由一个完全随机森林和一个随机森林训练产生类概率向量，最后通过拼接得到转换特征向量。

如图3 所示，多粒度扫描阶段分为特征扫描和特征转换2个过程。假设输入一个n维原始特征，滑动窗口大小为q维，滑动步长为k，滑动窗口扫描原始输入特征以提取特征信息，从而生成N个q维特征实例，计算式如下所示：

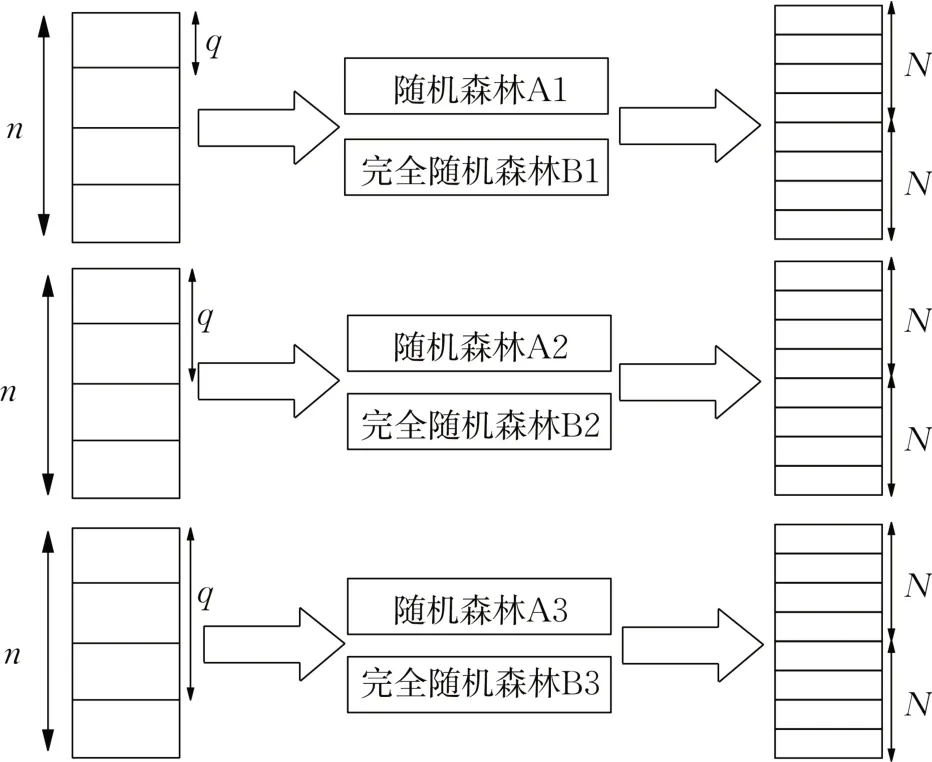
图3 多粒度扫描Fig.3 Multi-grain scanning

经过随机森林和完全随机森林训练后，每个森林输出s维类概率向量，然后将所有类概率向量连接为L维转换特征向量，L的计算式如下所示：

通过多粒度扫描得到的转换特征向量规模高于原始输入特征，可以提取更多的特征信息。

3.2 级联森林

级联森林逐层训练可以增强特征信息的表征能力，每一层采用不同的分类器对深度森林算法集成学习十分重要。因此，级联森林的每层结构包含完全随机森林和随机森林2 种不同的基础森林分类器。不同类型的森林分类器结合可以充分学习输入特征向量的特征信息，从而提高模型的整体性能。 图4为级联森林过程。

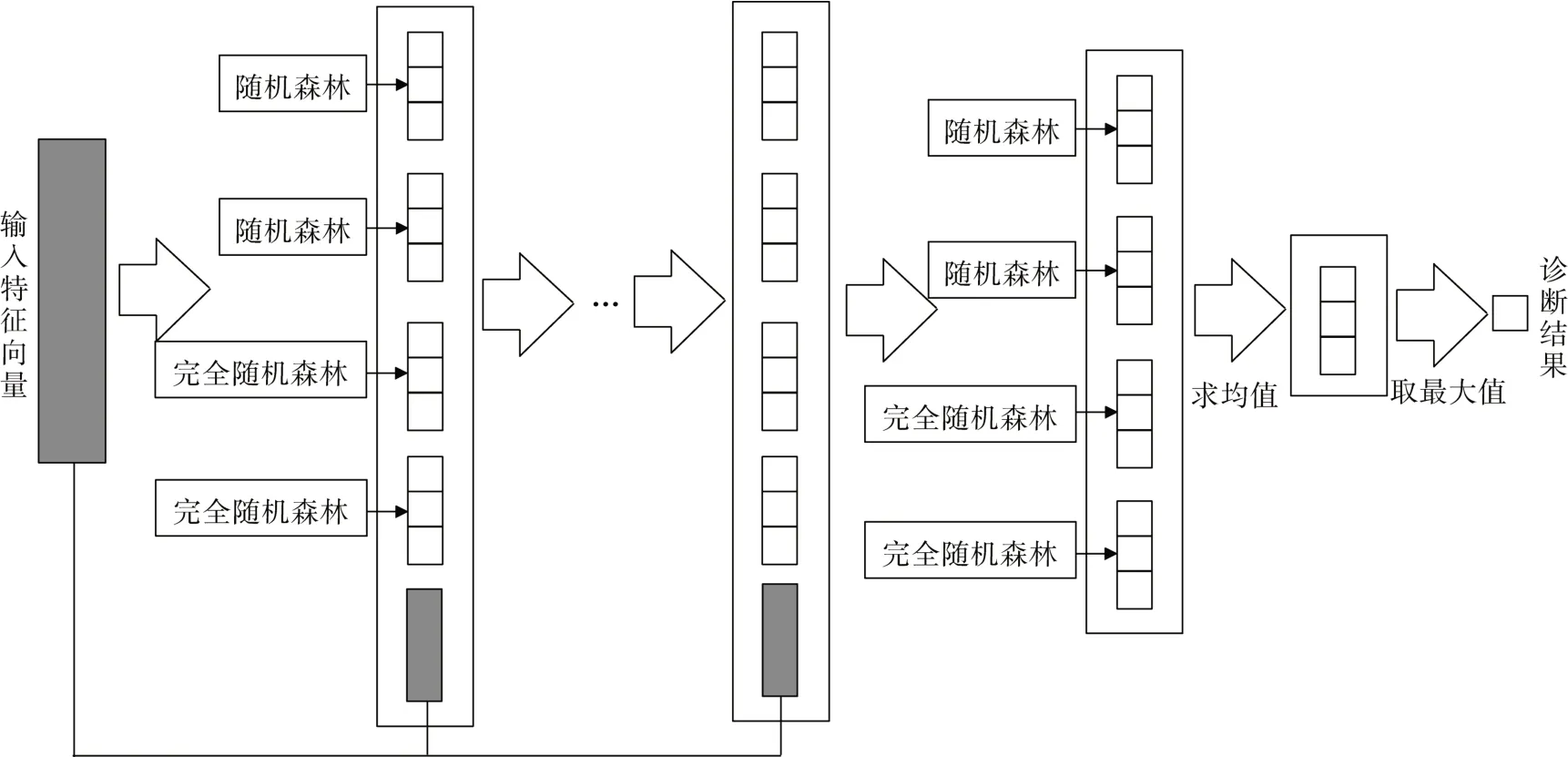
图4 级联森林Fig.4 Cascade forest

级联森林的输入特征向量是多粒度扫描阶段最终产生的特征向量，然后在级联层学习并训练，输出的类概率向量在逻辑回归前都没有合并，最终产生的类概率向量和原始特征向量拼接作为下一层的输入。逐层训练后，最后一层级联森林产生的所有类概率向量通过逻辑回归产生最终类概率向量，从中取最大值，得到原始输入特征向量的最终分类。

为了避免级联森林训练产生过拟合现象，每个完全随机森林和随机森林的训练都通过K折交叉验证后产生类概率向量。由于模型的级联层数可以自适应确定，因此每个级联层生成的类概率向量是动态更新的。如果模型在连续3层训练中没有明显的性能改进，级联过程就自动终止。此过程可以提高故障诊断准确率和减少训练时间。

3.3 改进深度森林模型原理

级联森林每一层级的特征变化太小，一些重要的特征可能会被削弱，而且训练也需要大量的级联层［15］。为了解决该问题，将主成分分析后的电流特征值嵌入模型并融合到传统深度森林算法生成的变换特征中以提高模型性能。

传统深度森林模型使用功率特征值数据进行故障诊断，改进的深度森林模型通过主成分分析将三段电流特征值作为一个独立输入并与其他向量拼接，以此作为级联森林输入，避免了传统深度森林的削弱。

主成分分析可以有效地减少电流故障特征值的特征个数，可以很好地解决深度森林算法在处理具有长特性单样本数据时的特征冗余、算法运行效率低等问题。改进的深度森林模型如图5所示。

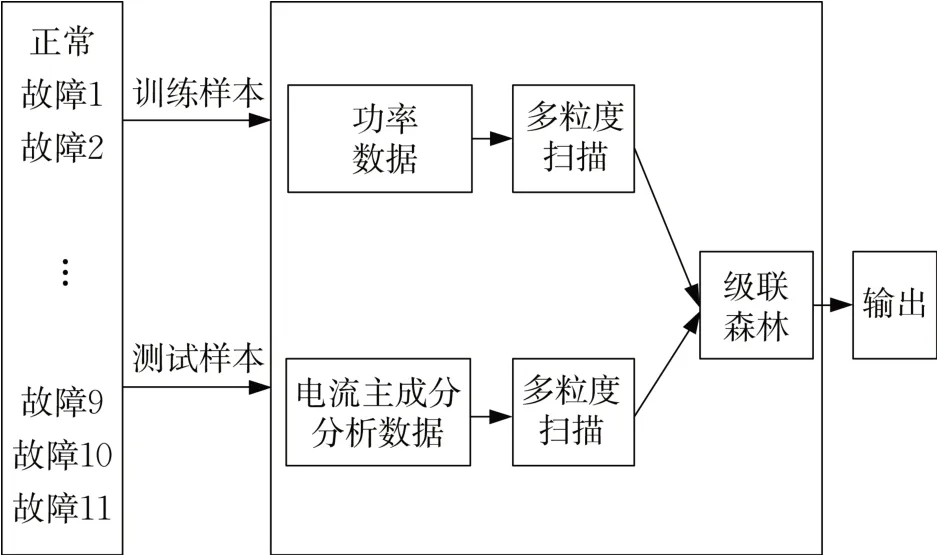
图5 改进深度森林模型Fig.5 Structure of improved gcForest model

3.4 性能指标

通过分类精度（Eaccuracy）、查准率（Eprecision）、查全率（Erecall）和F1对故障诊断进行评价。其中，F1为查准率和查全率的均值。Eaccuracy、Eprecision、Erecall和F1的计算式如下所示：

式中：ETP、ETN、EFP、EFN分别为真正例、真负例、假正例、假负例。

4 实验

为了验证该算法的有效性，以2016年—2018年广州铁路多个站点储存的S700K 转辙机电流、功率曲线为实验数据，原始数据集由正常样本和11种故障类型样本组成。数据集共1 200个样本，即每种故障100个样本，每个样本长为360。

在改进深度森林算法中，首先需要确定如表2所示的5个参数，分别是训练样本大小、多粒度扫描时级联森林的决策树数量、多粒度扫描时扫描窗口大小、数据切片步长、每个级联森林中包含的决策树数量。调整步长是有意义的，因为它直接决定了森林层数和训练时间，从而影响模型的准确性。在S700K转辙机动作功率曲线的局部特征中，5个样本点是最小识别粒度，所以实验中步长设为5。此外，对于3 个窗口的多粒度扫描，即40、90、120，在窗口的大小为40和120时模型可以识别锁阶段和转换阶段的特点，与窗口的大小为90 时呈现完全不同的特性［12］。

表2 参数选择Tab.2 Parameter selection

为了保证实验的准确性，交叉验证时采用取平均值的方法，每个案例运行10次。当训练数据占总数据的10%、20%、30%、40%时，验证12 类数据的诊断效果，得到的结果如图6所示。

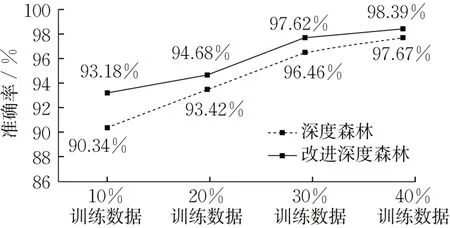
图6 10%～40%训练数据下S700K转辙机故障诊断精度对比Fig.6 Comparison of fault diagnosis accuracy for S700K switch machine between 10%～40%training data

图7 和图8 是2 种故障诊断方法在30%训练数据下的混淆矩阵。图7中，0代表正常情况，1～11分别代表11 种故障类型。改进深度森林算法的故障诊断精度为97.98%，深度森林算法的故障诊断精度为94.88%。可以看出，改进深度森林算法的诊断性能更优。

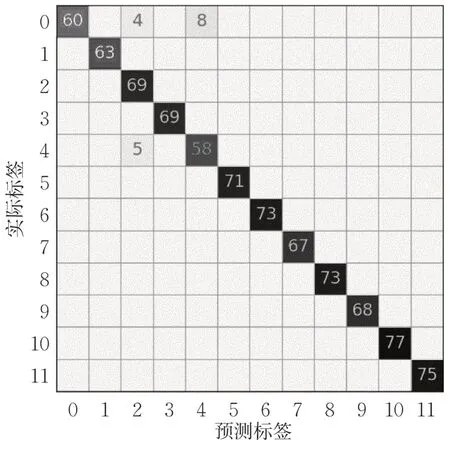
图7 30%训练数据下基于改进深度森林算法的S700K 转辙机故障诊断方法的混淆矩阵Fig.7 Confusion matrix of S700K switch machine fault diagnosis method based on improved gcForest algorithm at 30% training data

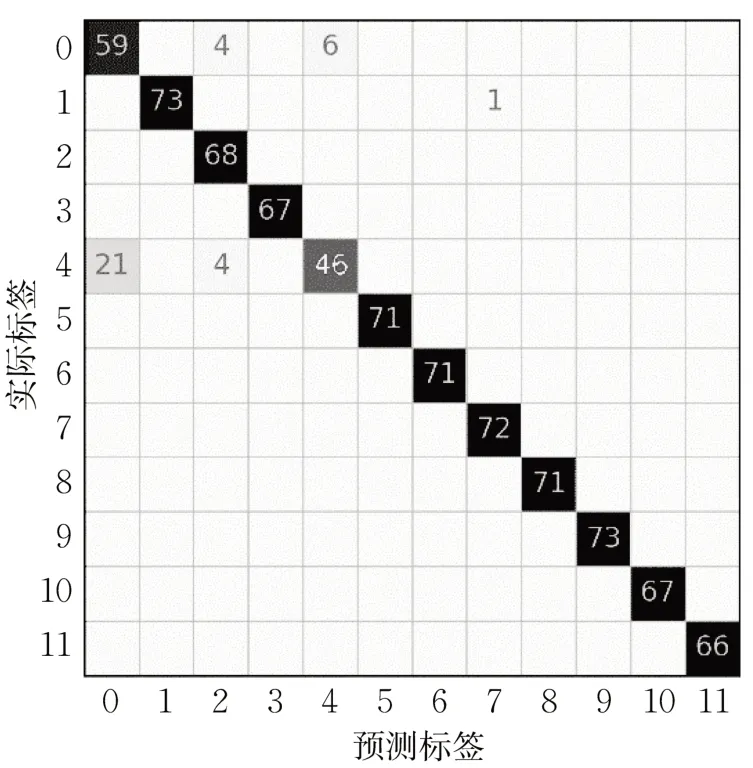
图8 30%训练数据下基于深度森林算法的S700K 转辙机故障诊断方法的混淆矩阵Fig.8 Confusion matrix of S700K switch machine fault diagnosis method based on gcForest algorithm at 30% training data

综上所述，基于改进深度森林算法的S700K 转辙机故障诊断方法相比基于深度森林算法的S700K转辙机故障诊断方法在各比例训练数据、各健康状态下都有更高的诊断精度。

为了验证所提模型的有效性，将所提模型与现有常用模型进行对比。表3为4种模型进行10次训练后得到的测试结果均值，分别为模型的精度和时间。与其他模型相比改进深度森林算法的故障诊断精度最高，达到了97.62%，并且在时间上也更短。

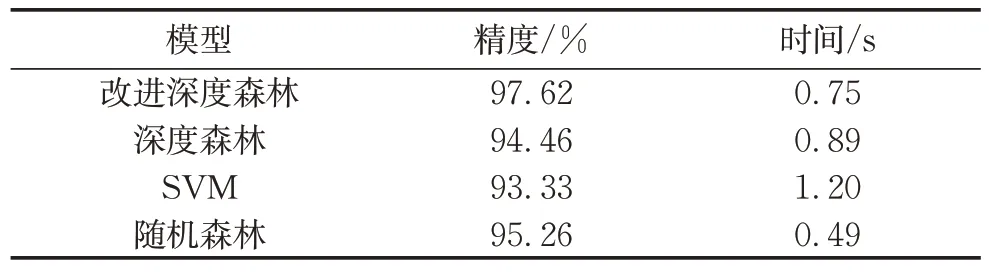
表3 改进深度森林模型故障诊断精度和其他模型对比Tab.3 Comparison of fault diagnosis accuracy between improved gcForest model and other models

5 结语

针对高速铁路S700K 转辙机的故障诊断问题，提出了一种基于主成分分析的改进深度森林故障诊断方法。首先使用主成分分析对电流数据进行特征简约，然后把简约后的特征值嵌入基于功率数据的深度森林模型。实验结果表明，与直接使用功率数据的深度森林故障诊断方法相比，提出的诊断方法具有更高的诊断精度，诊断精度达到97.62%。此外，还可以收集更多的数据以覆盖更多的故障类型，从而实现适用于现场环境的智能诊断方法，提高转辙机的维修效率。

作者贡献声明：

胡小晨：算法仿真与实验，论文写作。

郭 宁：思路梳理。

沈 拓：论文修改。

董德存：提出研究思路，参与研究方法。