高速铁路区间完全中断场景双向到发线运用优化

高博文， 欧冬秀， 董德存

（1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804）

随着铁路智能化进程的不断推进，越来越多的国家如中国、瑞士、荷兰、日本等相继提出了一系列调度辅助决策系统［1］。各类突发事件下的列车智能调整方法是近年来铁路运输组织领域研究的重点问题之一。铁路系统作为一个开环系统，列车运行过程不可避免地受到各类干扰因素的影响，从而产生列车延误。在这种情况下，调度员需要根据历史经验对延误列车的作业计划进行及时调整，但很难应对大范围的延误干扰。国内外学者运用各类数学模型模拟列车运行作业过程，并尝试利用计算机算法求解列车运行调整方案。Cacchiani 等［2］总结了列车运行实时调整的模型和算法。目前，对于小干扰事件的列车运行调整研究已经十分成熟，但缺乏对大干扰事件如中断事件的研究。

区间中断场景下，一旦中断事件发生，在中断事件恢复前列车将不被允许通过中断路段。Ghaemi等［3］引入浴缸模型来描述交通水平在中断事件下的变化。现有研究给出了解决列车运行调整问题的基本模型，按照模型类型大致可分为宏观和微观2 类。宏观模型侧重于整个运输网络，应用“事件-活动”网络重构列车时刻表，未考虑信号、列车速度和道岔切换等微观特征，而是将列车运行过程抽象为各个列车在各个车站到达和出发的事件集合以及连接任意2 个事件的活动集合［4-6］。宏观模型具有较低的计算复杂度，能够更有效地解决大范围列车运行调整问题。与此相反，微观模型关注运输网络的局部路段，需要获取列车和线路的详细信息，将运输网络抽象为一系列离散的行车资源，并通过构建等效的路网替代图来描述列车的运行过程［7-9］。微观模型着重描述列车的微观行为，更适用于解决局部路网中的列车运行调整问题。

无论采用宏观模型还是微观模型，选择合适的调度策略至关重要。科学合理的调度策略能显著减少中断事件对时空的影响，缩短列车恢复到正常运行的时间。城市轨道交通领域已有多种适用于中断场景的调度策略，包括灵活停站［10］、临时折返变更交路［10-11］、单线双向运行［12］、渡线反向行车［13］等。然而，由于旅客席位的预先预定，因此目前铁路领域的研究主要关注以下2 种策略：第1种，针对单线铁路和双线高速铁路，在完全中断场景下将列车依次扣停在中断事件上游车站的策略［14-15］；第2 种，针对区间部分中断场景，利用区间正常轨道列车交替通过中断区间的策略［16］。相比之下，铁路领域中可选择的调度策略十分有限，因此铁路领域中的调度策略设计和优化需要得到更多的关注。

针对高速铁路区间完全中断场景，提出了双向到发线运用优化策略。对于高速铁路小干扰［17-18］和中断场景［14-16］下的到发线运用研究均视双方向列车在车站内的作业相对独立，即每个列车仅使用车站内的正线和同侧到发线进行作业。考虑到大部分车站内的到发线具备双向作业条件，在文献［6］的基础上，运用“事件-活动”网络对区间完全中断场景下的列车运行调整问题和到发线运用策略进行建模，以列车作业间隔、车站到发线数量、调度调整策略等为约束，构建混合整数线性规划（MILP）模型。最后，通过实际案例展示双向到发线运用优化策略在列车运行调整方案中的优化效果。

1 问题描述

1.1 问题定义

我国高速铁路均为双线铁路，列车运行方向分为上行和下行方向。通常情况下，上、下行列车在区间和车站的运行相对独立，互不干扰。然而，若发生区间完全中断事件，则双向列车均无法通过中断区间，需在上游车站内等候修复。此时，调度员需根据列车的运行特征和位置，在中断事件期间为各列车分配停靠站点；待事件修复后，需合理安排列车发车次序，缩短作业时间，促使各列车尽快恢复正点运行。

图1a展示了一个区间完全中断场景下的列车运行调整案例，该线路共有6个车站（s1、s2，…，s6），每个车站到发线布置方式相同且共有4条到发线供列车作业使用。图1b展示了6个车站内的到发线布置情况。在正常情况下，2个方向上的列车数量相近。为避免交叉作业的影响，任意运行方向的列车仅使用车站内的正线及外侧到发线，即如图1b实线所示的2条列车作业径路。图1a中实线表示实际运行时刻表，虚线表示计划时刻表。中断发生后，已经进入中断区间的列车可以继续行驶，如列车g1；其余列车需要根据作业特征，由调度员按照经验扣停在中断区间上游车站，如列车g7、g9扣停在车站s2，列车g3、g5扣停在车站s3。

图1 区间完全中断情况下列车运行调整示例Fig.1 Example of timetable rescheduling in case of a complete blockage

目前针对我国高速铁路区间中断场景的列车运行调整，均是将车站内的上、下行列车分开作业，每个方向上的列车只能使用图1b 中的实线径路。实际上，每个车站的进、出站咽喉区具备多类渡线，使得一个方向上的列车能够利用对向到发线进行车站作业（如图1b 中对应的虚线径路）。由图1a 的调整结果可见，若列车能够更多地停靠在靠近中断区间的车站，则可以有效减缓事件影响向上游车站的传播速度。同时，由于在中断持续阶段受影响的列车（如列车g2、g4、g6、g8）无法通过中断区间，因此中断区间的下游车站（如车站s1、s2、s3）有大量到发线空闲。若这部分的到发线被合理利用起来，供对向受中断影响的列车（列车g3、g5、g7、g9）停靠或者通过作业，将有效减少中断事件引发的列车延误。

在区间中断事件发生后，考虑在中断区间2 个运行方向上的上游车站内，将对向到发线使用权限开放给受中断影响的列车使用。由于使用对向到发线有可能造成2个方向上的列车在到发线上的交叉运行，从而引发新的延误事件，因此需要对区间中断场景下双向到发线运用方式进行优化。提出了3个前提条件（参见3 节），在确保列车总延误不增加的情况下，令受影响的列车优先使用本运行方向的到发线；若本方向到发线均被占满，则根据列车总延误情况，酌情利用对向到发线进行作业。

1.2 问题假设

区间中断场景下的列车运行调整问题相对复杂，为简化模型，明确应用场景，作出如下假设：

（1）所有车站内的到发线均为配有乘降站台的双向到发线，并支持列车在任意到发线进行作业。

（2）所有区间均为双线区间，上、下行列车在区间内的作业相互独立、互不干扰。

（3）中断事件前，列车按计划时刻表准点运行。发生中断后，已进入中断区间的列车可正常通过，未进入中断区间的列车需在上游车站停车等待，称为“中断列车”。

（4）由于当日车次席位已售完，调整过程仅涉及作业次序和时间的变更，不考虑取消列车运行计划。

2 列车运行调整模型构建

2.1 问题抽象与参数定义

为了模拟列车在高速线路上的运行过程，从宏观角度将高速铁路网络抽象为由事件和活动构成的网络N=(E，A)。每个列车的运行过程被抽象为列车在各个车站si的到达事件d∈Earr，si和出发事件f∈Edep，si的集合；活动a∈A连接网络中的任意2个事件e1、e2，记录着事件间状态变化的时间间隔。按照2 个事件发生的列车主体te1、te2的不同，将活动集合A划分为单车运行活动集合Atrain和多车间隔活动集合Aheadway，集合Atrain表示同一列车主体在任意 车 站Atrain，si或任 意 区 间Atrain，ci的 运 行 活 动 集 合，集合Aheadway表示相邻的不同列车主体发生的事件间隔活动集合。集合S、C、G分别表示选定线路上的车站集合、区间集合和列车集合，si∈S，ci∈C表示下行列车依次经过的第i个车站与第i个区间。对于任意事件e，se、ge和re分别表示对应的作业车站、列车主体和运行方向。模型的输入参数和决策变量如表1 所示。

表1 参数定义Tab.1 Parameter definitions

2.2 基本模型

中断发生后，双向列车均无法通过中断区间，调度员需逐一扣停在线运行的列车。事件结束后，调度员需迅速安排扣停的列车发车，并采用压缩区间运行时间、车站作业时间以及变更越行关系等手段，使列车尽快恢复计划时刻。为减缓突发事件对列车运行的影响，优化目标主要为最小化列车到发事件与原定计划的时间偏移量。基于2.1 节定义的符号，得到不考虑事件影响的列车运行调整基本模型，如下所示：

目标函数式（1）表示最小化列车事件的调整时刻与计划时刻的偏差。式（2）表示各列车事件调整时间不得早于其计划时间；式（3）表示在突发事件发生前，各列车按照计划时刻表准点运行。式（4）和式（5）约束了计划时刻表中列车的作业类型。若计划中列车需要停站，则pgd，si等于1；若计划中列车不需要停站，则pgd，si根据调整情况取0 或1。式（5）表示列车在车站作业需要满足的最小停站时间约束。式（6）表示列车在区间作业时需要满足的最小运行时间约束（为避免列车在区间长时间运行，将区间纯运行时间最大值设置为各列车计划时刻表中的纯运行时间Tci，plan）。式（7）和式（8）共同约束了同一车站同一运行方向上的任意两列车的到达/出发事件间的最小间隔时间Tarr，arr/Tdep，dep；式（9）和式（10）共同约束了同一车站同一运行方向上同一到发线作业的任意两列车的出发事件和到达事件的最小间隔时间Tdep，arr。式（11）表示当列车到达事件d′发生时，车站至少存在一条空闲到发线可供列车使用，即车站容量约束。式（12）表示区间列车越行约束，车站si，rd表示车站si在运行方向rd的下一站。式（13）给出了各决策变量的取值范围。

2.3 调度策略建模

各方向上的列车在中断期间需依次扣停在车站，当且仅当中断事件恢复后才可发出。为实现这一控制策略，引入事件时序变量φe，h来记录事件e是否在某一时刻h前发生，其与xe的关系如下所示：

由事件时序变量φe，h可得区间完全中断场景下的列车调度策略约束，如下所示：

式（16）表示2 个运行方向上的列车无法在中断期间通过中断区间（车站sck，rf表示中断区间ck在运行方向rf的入口站）。式（17）中，Sck，r表示区间ck在运行方向r上的上游车站集合，si，r表示车站si在运行方向r的下一个车站。(∑φf，Hend-∑φd，Hend)表示中断期间车站si向下一站发出的且还未到站的列车数量，(∑φd′，Hend-∑φf′，Hend)表示中断期间在下一站扣留的列车数量。由于中断期间需要根据车站内的到发线数量进行扣车作业，因此(∑φf，Hend-∑φd，Hend)和(∑φd′，Hend-∑φf′，Hend)要小于等于下一站的到发线数量。

3 双向到发线运用优化建模

所提出的双向到发线运用优化策略允许在中断事件发生后的一定时间内，各方向受到影响的中断列车可以借助对向到发线进行扣车或通过作业。为避免对向到发线的使用给对向列车带来过多的延误影响，列车只有在本方向到发线均被占用且对向车站到发线有空余时，才可使用对向到发线进行作业。因此，使用对向到发线的列车到达事件d需要满足以下3个前提条件：

（1）事件d的发生时刻在规定的可以使用对向到发线的时间范围内。

（2）在事件d的发生时刻，车站内供本方向列车作业的到发线均被占用。

（3）在事件d的发生时刻，车站内供对向列车作业的到发线至少有一个可供使用。

为方便表述，假设车站si上运行方向为r的列车可以使用对向到发线，将另一个运行方向表示为r′。

3.1 新的活动间隔约束

需要增加的活动间隔约束主要由2类构成。第1 类，2 个运行方向r、r′上的列车有可能在对向到发线上交替作业，需要增加同一车站不同运行方向上列车到达、出发事件间的活动间隔约束；第2 类，运行方向r上的部分列车可能使用对向到发线，需要增加使用对向到发线的列车与其同运行方向使用本方向到发线的列车到达、出发事件间的活动间隔约束。新增的活动间隔约束如下所示：

式中：gê为ge1和ge2中的可能在对向到发线作业的列车主体；μgê，si为事件到发线0-1变量。

对于第1类活动间隔约束（re1≠re2），若2个事件e1、e2均为到达事件或者出发事件，则式（18）和式（19）共同约束了双向列车的到达间隔（T′e1，e2=T′arr，arr）和出发间隔（T′e1，e2=T′dep，dep）。当列车gê不在车站对向到发线作业时，为使λ′e1，e2或λ′e2，e1都等于零，需要增加约束，如下所示：

若2 个事件分别为到达事件和出发事件，则式（18）和式（19）共同约束了双向列车的到、发间隔或发、到间隔。当列车gê不在对向到发线作业时，为使λ′e1，e2或λ′e2，e1都等于零，需要增加约束，如下所示：

对于第2 类活动间隔约束（re1=re2），增加约束的方式与第1 类活动间隔约束相同，主要的区别是将运行方向为r′的列车主体替换成运行方向为r的列车主体，gê列车主体保持不变。

3.2 前提条件约束

为满足设定的3 个前提条件，需要对列车停站作业进行限制。首先，对于任意一个可以使用对向到发线的列车到达事件d，需要满足前提条件（1）。式（23）约束了当事件d发生在Hopen后，即对向到发线不再开放给列车使用时，μgd，si为零。

其次，为满足前提条件（2）和前提条件（3），需要对事件d发生时刻xd时车站内2 个运行方向r、r′上的车站到发线使用情况进行统计。2.2 节基础模型中的车站容量约束式（11）被替换为：

式中：m为时刻xd停在车站si内运行方向为r的列车数量；n为时刻xd停在车站si内运行方向为r′的列车数量；p为时刻xd停在车站si对向到发线上的运行方向为r的列车数量。式（24）、（25）约束了任意运行方向r上的到达事件d的车站容量。当μgd，si为0 时，即列车停在车站本方向到发线，(Gsi，r-(m-p))大于等于1，确保有到发线空闲；当μgd，si为1时，即列车停在车站的对向到发线，(Gsi，r-(m-p))等于0，(Gsi，r′-(p+n))大于等于1，确保前提条件（2）、（3）成立。式（26）共同约束了任意运行方向r′上的到达事件d′的车站作业。m′、p′的计算方法如下所示：

式中：m′表示时刻xd′停在车站si内运行方向为r′的列车数量；p′表示时刻xd′停在车站si内对向到发线上的运行方向为r的列车数量。为保证车站容量约束，当事件d′发生时，车站si内供给运行方向r′的到发线 应 至少 有一 个 空闲，即(Gsi，r′-m′-p′)大于等于1。

3.3 调度策略约束替换

由于开放了对向到发线作业的权限，部分列车gd可以停在下一站si，r的对向到发线，因此本站si可以发送更多的列车。2.3 节中的式（17）需要进行调整。为了统计中断列车在中断期间是否停靠在车站si，r的对向到发线，引入0-1 变量γgd，si。γgd，si与μgd，si、φd，Hend、φf，Hend的约束关系如下所示：

式（27）、（28）共同约束了当且仅当μgd，si为1、(φd，Hend-φf，Hend)为1（表示列车gd在中断期间未从车站si发出）时，γgd，si取1。根据变量γgd，si，式（17）需修改为

式（29）与式（17）的区别在于，若车站si发出的列车即将停靠在车站si，r内的对向到发线，或车站si，r中的中断列车已经停靠在对向到发线上，则不计入车站si的发车数量。

4 模型求解方法与有效不等式

构建的高速铁路列车运行调整模型属于混合整数线性规划模型的范畴并属于NP-hard问题。目前对于此类问题的求解，商业求解软件如Gurobi、Cplex 等可在短时间内提供有效的解决方案。考虑到优化软件Gurobi可以利用多核处理器进行并行计算，采用Gurobi求解器对构建的模型进行求解。

利用求解器求解需要消耗一些时间（假设为HGurobi），这使得在时段[Hstart，Hstart+HGurobi)内无法提供可行列车调整方案。为贴合现场实时性的需求，利用自编算法对2 个方向上的在线列车按照计划时刻表中的作业次序依次进行扣停作业（耗时在几毫秒内），输出的调整方案将供该时段使用，构建的列车运行调整模型仅对(Hstart+HGurobi)时刻后的列车作业进行调整。

为了进一步加快列车运行调整模型的求解速度，在求解过程中添加了一些有效不等式，这些不等式均是由同一列车的到达、出发事件的有序性而产生的。添加的有效不等式如下所示：

5 算例分析

5.1 场景描述

算例数据来源于2019 年广珠城际高速铁路深湛线部分路段的运行图数据。整个线路从新会站至茂名站，沿线经过13 个车站、12 个区间。计划时刻表中包含29 对上、下行列车数据，列车速度等级相同。各车站到发线数量配置如表2 所示，其中(a，b)表示该站正常情况下供上行列车作业的到发线数为a，供下行列车作业的到发线数为b。

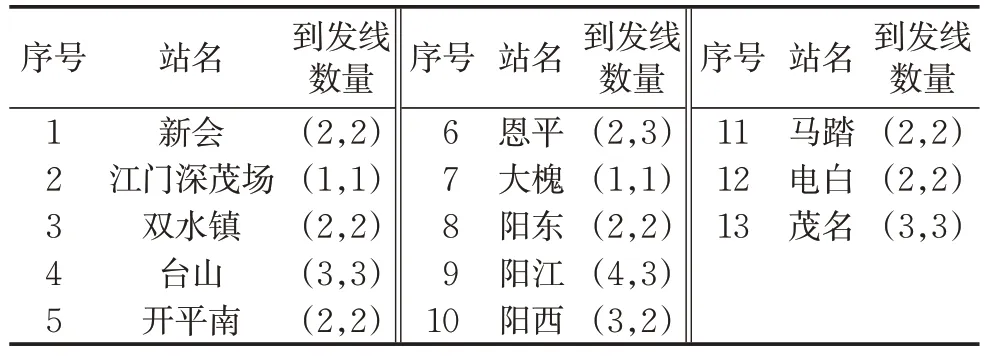
表2 车站到发线数量Tab.2 Number of station tracks

各区间最小纯运行时间如表3 所示，其中(a，b)依次表示上、下行的最小纯运行时间，单位为min。

表3 区间最小纯运行时间Tab.3 Pure running time of segments

结合线路不同时段内列车开行密度的特征，通过设定中断事件的发生区间ck和开始时间Hstart，构建了3个中断场景；每个中断场景下，通过调整中断事件持续时间又衍生了3个中断案例。详细的场景信息如表4 所示。其中，中断场景(a，b，c)表示中断事件发生在a区间、b时刻，共持续cmin。

表4 完全中断场景信息Tab.4 Information of complete blockage scenarios

参照文献［15-16］，同方向列车作业间隔Tarr，arr、Tdep，dep、Tdep，arr分别设置为3、2、3 min。停靠在对向到发线的列车与其同运行方向的其他列车的额外间隔时间与同向列车间隔时间设置相同。停靠在对向到发线的列车与其对向列车间的作业间隔T′arr，arr、T′dep，dep、T′dep，arr设置为0、0、3 min。列车最小停站时间Tsi设置为2 min，列车启、停附加时间Δacce、Δdece均设置为1 min。对向到发线使用权限开放时间默认设为[Hstart，Hend+60 min]，参数M取1 440 min。

所有算例均在CPU 为Inter（R） Core（TM） i7-12700K、内存为32 GB、操作系统为Windows11 的64 位台式机上运用Python 平台构建列车运行调整模型，并调用Gurobi 9.5.1 求解（最大求解时间HGurobi取5 min）。

5.2 到发线运用优化前后结果对比

为了比较双向到发线运用优化前后的结果，针对每个中断案例构建了2类列车运行调整模型。第1类列车运行调整模型中不添加3节中的优化约束，每列车仅使用本运行方向到发线进行作业；第2 类列车运行调整模型在中断事件发生后使用双向到发线运用优化策略。表5 展示了9 个中断案例的调整结果。

表5 不同中断案例下的列车运行调整结果Tab.5 Results for different blockage cases

表5 中每个中断案例下2 类模型的求解Gap 均小于等于0.03，说明所提出的模型均可在5 min内快速获得较优甚至最优的列车运行调整方案。对比2类模型的求解结果，除了中断场景（9，16，60）外，其余案例均通过使用对向到发线减少了列车总延误时间。随着中断事件影响的增大，列车对于对向到发线的使用次数也逐渐增加，并且列车每使用一次对向到发线对总延误的优化效果也随之变得显著。在这8 个案例中，平均每使用一次对向到发线将有效减少219.4 min 的列车延误。在案例（9，16，60）中，中断事件的影响相对较小，仅使用本方向到发线便可以很好地控制延误的传播，因此2 类模型输出了同一种列车运行调整方案。为了更形象地显示2类模型输出的列车运行调整方案的差异，图2a和图2b（圆点表示对向到发线作业上的到达事件和出发事件）展示了案例（9，16，180）的2类模型输出结果。

图2 中断场景（9，16，180）的列车运行调整方案Fig.2 Final timetable for blockage scenario (9,16,180)

由图2a 可知，中断事件的影响在下行和上行方向已经传播到了序号为6 和13 的车站。从图2b 来看，由于开放了对向到发线，中断事件的影响在下行和上行方向仅传播到了序号为9和11的车站。综合求解时间和求解方案的优劣，9个案例的测试结果反映出所提出的双向到发线运用优化策略可以根据中断事件的影响范围，在必要时充分利用对向到发线为中断列车提供更多的作业选择，在不影响对向列车作业的前提下，极大程度地减少中断事件造成的列车延误影响。

5.3 对向到发线开放时长灵敏度分析

在前文案例中，默认将对向到发线开放的时长设定为60 min。为了研究对向到发线开放时长对最终结果的影响，保持其他模型参数不变，将对向到发线的开放时长分别修改为0、30、90 min，获得的最终列车延误结果如图3 所示。图3 中，以开放时长0 min下的调整结果为基线，展示了各个案例其他开放时长下的调整结果与该基线的差值。

图3 不同对向到发线开放时长下的目标函数值Fig.3 Objective function values for different opening times

随着开放时长由Hend逐渐增加至Hend+60 min，案例2、3、9的列车延误数值有小幅下降，但延误改善效果并不明显。当开放时长继续增加至Hend+90 min时，案例3、6、9的列车总延误数值有所上升。3个案例均是3个中断场景中影响范围最大的，延长对向到发线的开放时间造成解空间的进一步扩大，加上将最大求解时间设置为5 min，有限的算力使得求解器求得了一个较差的解。综合测试结果可知，在小范围中断事件中可适度延长开放时间，而在大范围中断事件中宜缩短开放时间，以确保算力充足。

6 结语

提出了双向到发线运用优化策略，允许中断列车在部分车站使用对向到发线，以最小化列车总延误时间为目标构建混合整数线性规划模型。以广珠城际高速铁路为例，构建了9 个中断案例。结果表明，基于双向到发线运用优化策略的模型输出的调整方案受中断影响范围更小，列车总延误时间更少。中断列车每使用一次对向到发线，平均减少219.4 min的列车延误。

作者贡献声明：

高博文：模型设计与程序实现，最终版本修订。

欧冬秀：提出双向到发线运用优化方案。

董德存：区间中断场景下列车运行调整方案可行性验证。