巧用定义求解高中数学圆锥曲线方程
2024-01-09王曦
王 曦
(吉林省长春市一三七中学,吉林 长春 130052)
高中数学是一门逻辑性和抽象性很强的学科.学生在求解圆锥曲线难题时,往往找不到解题的思路和方法,不仅耗费了较多的解题时间,还导致解题的准确率也不高.如何提高高中学生求解圆锥曲线题目的准确率和解题效率呢?求解圆锥曲线难题的关键在于核心知识点的理解、掌握,以及根据题目要求合理地运用相关知识点.
圆锥曲线的核心知识点中,圆锥曲线的定义是推导轨迹方程和几何性质的基础,也是重要的解题工具.本文重点阐述了运用定义求解圆锥曲线轨迹方程的技巧.
1 圆锥曲线思维导图
运用定义求解圆锥曲线难题,首先需要理解和掌握圆锥曲线的定义.本文以人教A版高中数学选修第三章《圆锥曲线的方程》“圆锥曲线”为例,借助思维导图,以更加直观、形象的方式导入圆锥曲线知识框架.

图1 圆锥曲线思维导图
椭圆和双曲线都有两种定义.一是根据平面内某个动点与两个定点的距离之和,或者之差与定长的关系进行定义.例如,椭圆的定义:若一个动点P到平面内2个定点M和N的距离等于定长L,则该点所在的轨迹为椭圆.表达式为PM+PN=L(L>MN).再如双曲线的定义:若一个动点P到平面内2个定点M和N的距离之差等于定长L,则该点所在的轨迹为双曲线.表达式为PM-PN=L(0 二是根据平面内某个动点到定点的距离与该动点到定直线距离的比值进行定义.例如,椭圆、双曲线的定义:一个动点P到平面内定点M的距离与到定直线的距离L之比为一个常数e.若该常数e的取值范围为0 抛物线只有一种定义.若一个动点P到平面内定点M的距离与到定直线的距离L之比为一个常数e.若该常数e的取值范围为e=1,则该动点所在的轨迹为抛物线.表达式为PM/L=e(e=1)[1]. 若一个动点到平面内2个定点的距离等于定长,则该动点所在的轨迹为椭圆.运用定义巧解椭圆轨迹方程如例1所示. 例1如果点P在圆O上,圆O的方程为x2+y2=25,点F的坐标为(2,0),线段FP的垂直平分线与线段OP相交于点M.那么,动点M所在轨迹的方程是什么? 分析根据题意“线段FP的垂直平分线与线段OP相交于点M”,如图1所示,以及MP=MF,MF+MO=OP=3=2a,可以变换为“点M(x,y)到点P的距离与到点F(2,0)的距离之和等于定长3”.然后,根据椭圆的定义,可以确认点F、点O为椭圆的焦点,2c=2,c=1. 求解:按照椭圆的定义,以及MF=MP,点M(x,y)到点O(0,0)的距离MO与到点F(2,0)的距离MF之和MO+MF等于定长OP”,OP为圆O的半径3,2a=5. 小结根据平面内某个动点到2个定点的距离之和与定长的线段长度之间的关系进行转换,若转换为相等关系,则该动点在平面内的轨迹为椭圆[2]. 若一个动点到平面内定点距离与到定直线的距离相等,则该动点所在的轨迹为抛物线.运用定义巧解抛物线轨迹方程,具体如例2所述. 图2 点M的轨迹 图3 点A的轨迹 例2如果点A到直线x=3的距离与点A到点(-2,0)的距离大1,那么,动点A所在的轨迹的方程是什么? 根据抛物线的标准方程y2=-2px,求得抛物线的方程为y2=-8x. 若一个动点到平面内2个定点的距离之差等于定长,则该动点所在的轨迹为双曲线.运用双曲线的定义,巧解其轨迹方程,具体如例3、例4所述. 图3 动圆与定圆的相切关系 图4 双曲线C 例3已知动圆P与两个定圆(圆F1和圆F2)之间的关系都相切,并且,圆F1和圆F2之间的关系为相离,距离为8,以及半径分别为3和1.求解动点P的轨迹? 求解:令动圆P的半径为R,两个定圆(圆F1和圆F2)的半径分别为r1、r2.根据题意,将动圆P与两个定圆(圆F1和圆F2)之间的相切关系,分为两种情况: 一是动圆P与两个定圆(圆F1和圆F2)之间外切的情形.如图3-1所示,根据动圆的半径R与定圆的半径r1、r2之间的差值为r1-r2,可以判断动圆的圆心P与两个定圆的圆心F1和F2之间的距离之差为定长,并且,小于两个定圆圆心之间的距离|F1F2|,如以下公式所述. |PF1|-|PF2|=(R+r1)-(R+r2)=r1-r2<|F1F2|,得出动点P的轨迹为靠近焦点F2的一支双曲线. r1-r2=2a=4,求得a=2.结合2c=8,求得c=4.进而求得b2=12. 二是动圆P与两个定圆(圆F1和圆F2)之间内切的情形.如图3-2所示,根据动圆的半径R与定圆的半径r1、r2之间的差值为r1-r2,可以判断动圆的圆心P与两个定圆的圆心F1和F2之间的距离之差为定长,并且小于两个定圆圆心之间的距离|F1F2|,如以下公式所述. |PF1|-|PF2|=(R+r1)-(R+r2)=r1-r2<|F1F2|,得出动点P的轨迹为靠近焦点F1的一支双曲线. r1-r2=2a=4,求得a=2.结合2c=8,求得c=4.进而求得,b2=12. 化简后,得到c2-a2=5. 运用定义法求解圆锥曲线难题,可以提高高中学生求解圆锥曲线题目的准确率和解题效率.通过定义法确定了动点轨迹为椭圆、抛物线和双曲线等圆锥曲线,然后,分别根据椭圆、抛物线和双曲线等圆锥曲线的定义和几何性质求解椭圆、抛物线和双曲线等圆锥曲线轨迹的标准方程.2 巧用定义求解圆锥曲线方程
2.1 巧用定义求解椭圆方程
2.2 巧用定义求解抛物线方程

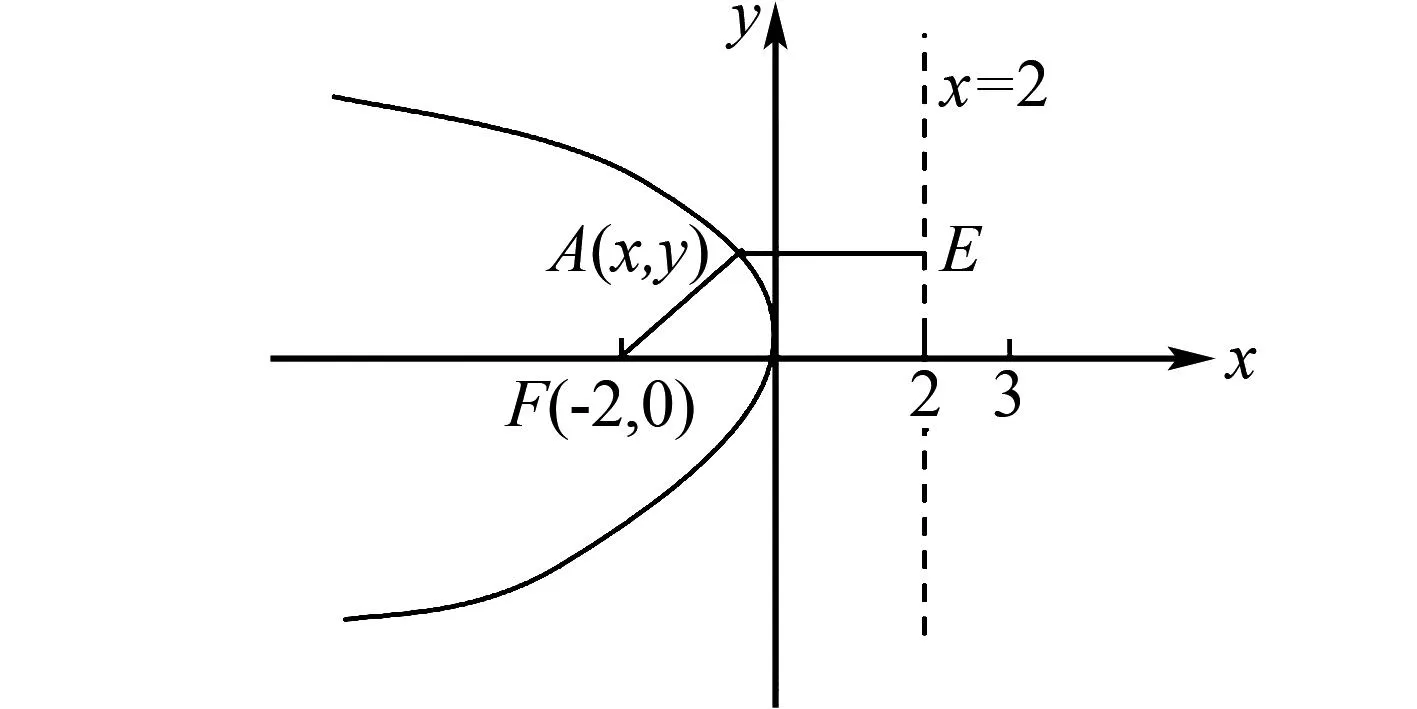

2.3 巧用定义求解双曲线方程