一类考虑未垂直传播新生儿的预防接种及人均病床数的SIVS乙肝传染病模型分析
2024-01-09高汝林
王 琪,傅 霞,高汝林
(陕西工业职业技术学院,陕西 咸阳 712000)
经典的SIR、SIS传染病模型通常根据康复类人群分为不同研究方向[1-2],而文献[3]基于实际情形中疫苗具有接种效率,在传统SIS模型三类人群基础上考虑加入一类暂时免疫的接种者仓室V。学者对这类模型进行研究发现,当考虑疫苗接种效率时,模型可能发生后向分支[4-7]。本研究主要基于乙型肝炎病毒传播机制在文献[8]的基础上研究易感者、接种者新生儿及未发生垂直传播新生儿的预防接种及存在一定疫苗接种效率时对乙肝病毒传播的影响。模型考虑引入文献[9]定义的饱和治疗函数,该函数与医疗资源人均病床数有关:
其中,μ0,μ1分别为最小和最大的疾病恢复率,此时疾病会发生各类分支,可有效调节医疗资源数量,控制疾病流行。
基于乙肝病毒传播机制建立一类考虑新生儿的预防接种、接种效率及人均病床数量的SIVS传染病模型,在文献[8]的基础上对加入未垂直传播新生儿预防接种因素的乙肝传染病模型进行研究。
1 模型建立
若某一地区共具有三类人群仓室,即易感者、染病者及接种者仓室,作出如下假设:
①该地区不发生人口迁入、迁出及因病死亡。②该传染病的发生采用双线性发生率。③该地区人口的出生率相等自然死亡率。
由于该地区总人口恒定,设S(t)、I(t)、V(t)分别表示在t时刻该地区易感者、染病者及接种者占总人口的比例。由于乙肝染病概率与年龄结构有关,将疫苗接种分为对易感者、接种者、未发生垂直传播新生儿的疫苗接种及对易感者的接种,相应接种比例分别表示为m、m′。由于疫苗接种具有一定效率,接种后的人群与染病者接触后仍可能染病,将疫苗接种效率记为σ,σ∈(0,1),当σ=0时,疫苗接种完全有效,当σ=1时,疫苗接种完全失效。将疾病垂直传播率记为q,染病者与易感者及接种者的有效接触率记为β,该地区人口的出生率及死亡率分别记为b、d,则b=d。μ为治疗函数,与人均病床数量δ有关。θ表示疫苗接种的失效比例。
传播流程机制如图1。
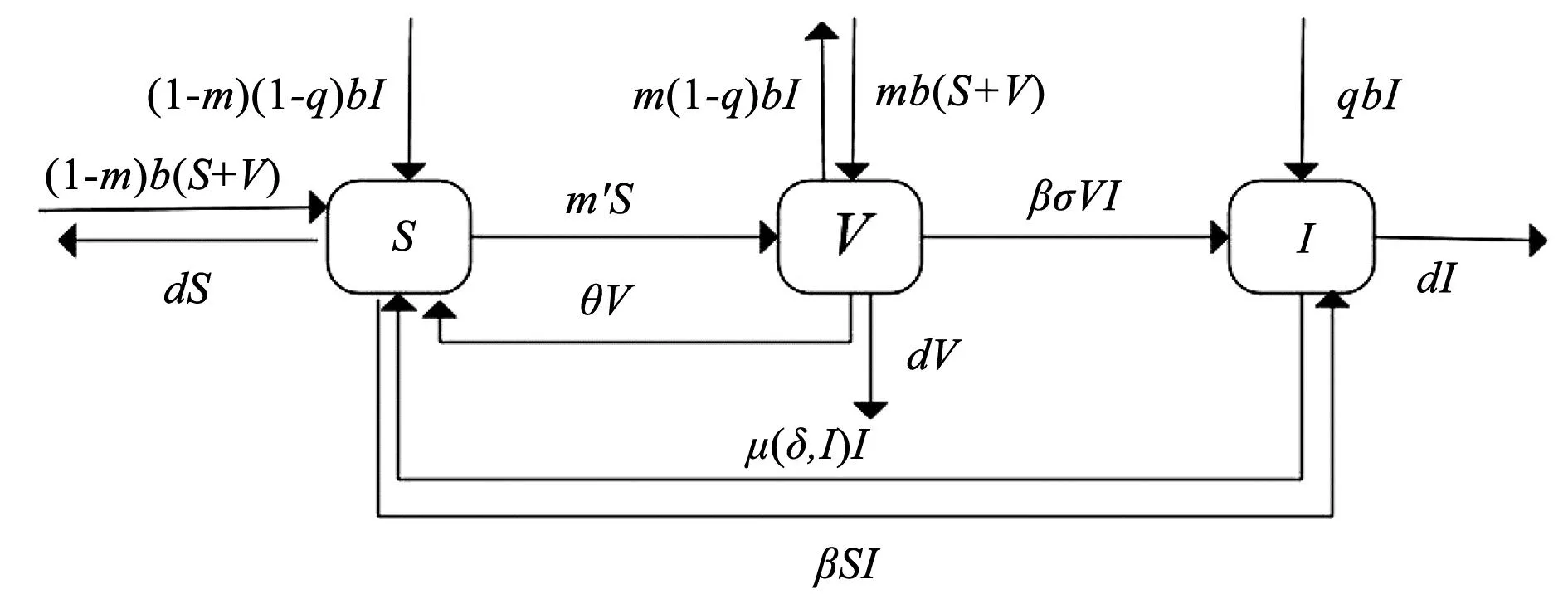
图1 传染病传播机制Fig.1 Infectious disease transmission mechanism
根据乙肝病毒传播过程,建立如下模型:
(1)
由于S=1-I-V,对上述模型(1)进行降维,得到模型(2):
(2)
2 主要结果
2.1 基本再生数

现将根据第二代生成矩阵法计算基本再生数R0,则:
通过矩阵F,V在无病平衡点E0处的Jacobi矩阵,计算得出疾病的基本再生数表达式:
(3)
由于上述模型中各参数均取值(0,1),则有b>(1-σ)mb,则R0>0一定成立。
2.2 平衡点的存在性
根据无病平衡点计算结果,无病平衡点E0始终存在。对于地方病平衡点的存在性展开讨论:
H(I)=β2σI3+h1I2+h2I+h3=0
(4)
其中:
h1=β[m′+θ+b+(σ-1)(mb+m′)+(σ-1)(1-q)mb]+βσ[μ0+(1-q)b]+β2σ(δ-1)
h2=β(1-σ)(1-δ)(mb+m′)-β(1-δ)(m′+θ+b)-β2σδ+[μ0+(1-q)b](m′+θ+b)+βσδμ1+β(1-q)bδ[m+σ(1-m)]
h3=δ(m′+θ+b)[μ1+(1-q)b](1-R0)
由于上述三次方程求根过程较为复杂,利用几何法探究地方病平衡点的存在性。
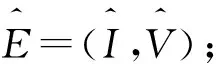
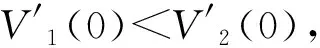

学术论文摘要是一种独立的语篇,用词规范,描述客观,使用语法和词汇衔接手段构成连贯的语篇。但由于英汉民族的思维方式的不同,由此导致了两种语言在摘要语篇衔接使用上的差异。英文摘要多用显性连接,使用照应和连接衔接方式;而中文摘要多用名词隐性连接,利用重复来表示照应关系。翻译时,需先分析句子的功能意义,才能确定句子的结构形式。
证明:由于V关于I的函数满足V1(I)=V2(I),其中:

探究V1(I)与V2(I)的单调性及凹凸性。
由上述判断可知,V1(I)在[0,1]上单调递减且为凹函数,V2(I)是在[0,1]的凸函数。又由于:
则V1(0)>V2(0)⟺R0<1;V1(0)=V2(0)⟺R0=1;V1(0)
综上,得到地方病平衡点存在3种情形:
情形①:若R0>1,且V1(0)

图2 V1(I)和V2(I)的函数关系Fig.2 Functional relationship of V1(I)和V2(I)

成立时,V1(I)与V2(I)在[0,1]内有且仅有一个交点,否则不存在交点[如图2(b)]。


2.3 平衡点稳定性
定理2:模型(2)无病平衡点稳定性结论如下:
当R0<1时,模型(2)的无病平衡点E0在D内局部渐近稳定;当R0>1时,E0不稳定;当R0=1时,E0为鞍结点,其中当C>0时,E0为右鞍左结点,当C<0时,E0为左鞍右结点。
证明:模型(2)的Jacobi矩阵为:
则在E0点处的Jacobi矩阵为:
若R0-1<0,即R0<1时,J(E0)存在两个负实部特征根,此时E0在D内局部渐近稳定;若R0-1>0,即R0>1时,J(E0)存在两个异号特征根,此时E0为鞍点不稳定。若R0-1=0,J(E0)分别存在一个零实部和负实部特征根,属于临界情形下无病平衡点稳定性分析。现根据Liapunov-Schmidt更替法,按照文献[10]思路展开分析。
(5)
2)利用二元函数麦克劳林展式将方程右端函数展开,得到模型(6):
(6)

3)令模型(6)右端函数为0,当|x|≪1时,可通过待定系数得到V′关于I′的函数。令V′(I′)=a1I′+a2I′2+O(I′3),则:
得到:
则V′与I′的关系可表示为:
代回模型(6)第一式中,得到一个一维系统:
+O(I′3)
它的一个普适开折拓扑等价于:
根据其轨线的拓扑分类,在R0=1时,无病平衡点E0为鞍结点。
令:
具体地,当C>0时,E0为右鞍左结点;当C<0时,E0为左鞍右结点。

2)若R0<1,在定理2[3)]条件下模型存在两个地方病平衡点,其中E1=(I1,V1)为鞍点始终不稳定,E2=(I2,V2)是非鞍点,在D>0时局部渐近稳定。
该矩阵特征方程为:
其中:
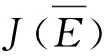
2.4 后向分支
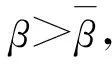


根据文献[11]中定理计算A,B,将模型(6)线性部分构成的矩阵记为Y,设其在零特征根处的非负左、右特征向量分别为υ,ω。
其中:
得到相应的左右特征向量分别为:

其余分量的二阶求导均为0。则:


在R0=1时,若A>0,B>0,系统会出现后向分支。由于B>0恒成立,只需寻找A>0条件。即:
则有:
β(1-σ)δ(mbq+m′)(m′+θ+b)+β2σ(1-σ)δ(mb+m′)-βδ(m′+θ+b)2>(μ0-μ1)(m′+θ+b)2
(7)
由式(7)看出,若满足:
(1-σ)(m′+θ+b)(mbq+m′)+βσ(1-σ)(mb+m′)>(m′+θ+b)2
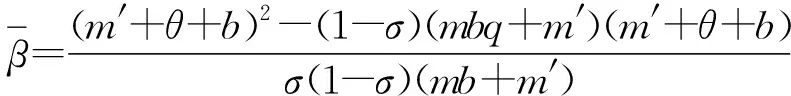
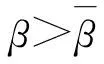

β(m′+θ+b)2-β(1-σ)(mbq+m′)(m′+θ
即:
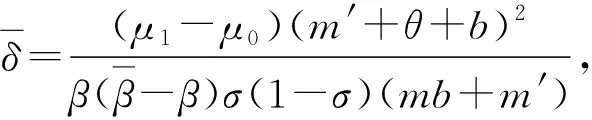
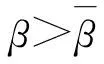
3 数值模拟
3.1 平衡点存在性及稳定性数值模拟结果


图3 模型在δ=0.1恒定时轨迹Fig.3 Constant trajectories of the model at δ=0.1
固定参数μ0=0.1,μ1=0.6,θ=0.1,m′=0.4,m=0.6,σ=0.2,b=0.06,q=0.06,保持β=0.7恒定,绘制δ不同取值时模型(2)轨迹。取δ=0.05,模型具有一个局部稳定的无病平衡点E0,见图4(a);取δ=0.002,模型具有一个鞍点E1、一个稳定结点E2及一个稳定的无病平衡点E0,见图4(b)。

图4 模型在β=0.7恒定时轨迹Fig.4 Constant trajectories of the model at β=0.7
3.2 后向分支数值模拟结果
固定参数σ=0.65,m′=0.4,θ=0.7,m=0.6,b=0.2,q=0.2,μ0=0.2,μ1=0.6。取β=1.2,δ=0.3,模型(2)产生后向分支,见图5(a),当R0<1时,模型同时具有局部稳定的无病平衡点和两个地方病平衡点,其中不稳定的鞍点会随R0的增大而逐渐消无,稳定的平衡点始终存在。取β=0.3,δ=0.3,模型产生前向分支,见图5(b),当R0<1时,只存在一个稳定的无病平衡点,R0>1时,存在唯一稳定的地方病平衡点。

图5 模型后向分支和前向分支Fig.5 Models backward and forward branch
4 结论
基于文献[8]建立的模型,本研究基于乙型肝炎传染病传播机制考虑加入对未垂直传播新生儿进行预防接种因素,在具有一定疫苗接种效率的实际情况下建立了一类对两类新生儿接种、易感者接种及人均病床数的SIVS乙肝传染病模型。通过分析模型得到了对乙肝传染病防治工作有效的理论指导,包括以下结论:
当R0>1时,染病者比例随时间变化逐渐保持稳定;当R0<1且人均病床数大于某一定值时,染病者比例随时间变化逐渐消亡。
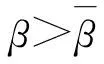
通过比较文献[8]与本模型后向分支产生条件:
文献[8]中发生后向分支的范围为:
本模型发生后向分支的范围为:

通过尽可能减少染病者与易感者、接种者之间的有效接触,合理增加医疗资源,可以避免模型发生后向分支,达到有效防治疾病的效果。提高对易感者与接种者新生儿及对未发生垂直传播新生儿的疫苗接种比例及持续研究疫苗增加接种效率可有效控制乙肝流行。
