基于最小二乘法的某型号程控电阻箱示数校正算法研究

2024-01-09张晓勇

黑龙江科学 2023年24期

张晓勇

(鹤壁职业技术学院,河南鹤壁 458030)

0 引言

程控电阻箱是电学测量的重要精密仪器之一,在工业机器人、数控机床、机器视觉、智能汽车、芯片生产等智能制造领域的元器件生产中发挥着重要作用。在工程科学领域,由于测量要素(如仪器仪表、计算方法、环境变化等)不能达到最高标准,往往导致测量对象的真值与测量结果之间存在一定的偏差,在计算数学中统称为测量误差。目前,学者针对如何评估、校正、降低测量读数动态误差这类问题提出了许多经典算法,如小波变换、遗传算法、樽海鞘算法、卡尔曼滤波法、BP神经网络法、时间序列分析法等[1-6],取得了一定的效果,因此构造有效算法对提高电阻箱输出电阻的精确度并实现智能制造行业的快速、稳定、高质量发展具有重要的推动作用。

1 算法介绍

1.1 程控电阻箱

某型号程控电阻箱的内部结构如图1所示。

图1 某型号程控电阻箱的内部结构Fig.1 Internal structure of a type of programmed resistance box

从图1可以看出,由于连接导线固有电阻、旋转开关触头接触电阻、输出端子固有电阻的存在,实际的输出电阻不可能达到0 Ω。图中的r表示电路中的固有电阻,也称为最小电阻。本电阻箱的最小电阻r规定为0.01 Ω(这是经多次实测后给定的平均数值)。电阻箱的电阻调节范围为0.01～100 000.00 Ω,最小步进值为0.01 Ω。

1.2 算法假设

为了避免变阻箱校正问题过于复杂,考虑变阻箱的自身属性与工作环境,提出以下几点研究假设:

A.变阻箱工作时的状态保持持续稳定,受外界条件的影响较小,可忽略不计。

B.固有电阻为最小电阻(0.01 Ω)。

C.根据实验过程中搜集的数据可视化结果,给定值与测量绝对误差近似为线性关系(如图2所示),由此提出假设:绝对误差随着给定电阻值的级数(步长为10)增长呈现线性叠加。

图2 某型号程控电阻箱的给定值与绝对误差间的线性拟合及误差Fig.2 Linear fitting and error between the given value and the absolute error of a programmable resistance box of a certain type

1.3 符号变量

为了使算法的建立过程更为方便、高效,定义以下几个量并用相应的字母符号表示。如不加特殊或专一说明,所列的字母符号均表示对应的量。各个字母符号及其对应表示的量如下:

g(j):各倍率档位的给定值;s(j):各倍率档位的实际测量值;c(j):各倍率档位的校正值;r(j):各倍率档位的相对误差(%);sc:要求的实际电阻值;sj:要求的实际电阻值的校正值;sk:首次校正值对应的实际电阻值;Rk:首次校正值对应的实际电阻值与sc之间的绝对误差;j:1～63,各倍率的序列号。

1.4 算法设计

根据研究假设C,本模型对各挡位电阻的绝对误差与给定值之间的相关性系数进行求解,公式为:

(1)

当相关性系数R值超过0.9时,尝试找到各档位倍率的校正值,具体如下:

(2)

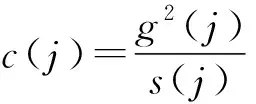
(2′)

在上述算法模型基本假设的基础上尝试建立相应的数学模型,对要求的实际电阻值sc(sc∈[0.01,99 999.99])进行档位拆分,阻值拆分公式具体如下:

(3)

这里以实际电阻值sc=88 888.88 Ω为例,按照式(3)进行拆分,结果如下:

88 888.88=8×104+8×103+8×102+8×101

+8×100+8×10-1+8×10-2

如此便可得到:

k(1)=8,k(2)=8,k(3)=8,k(4)=8,

k(5)=8,k(6)=8,k(7)=8

k(i)的矫正过程具体如图3所示:

图3 实际电阻的拆分及校正Fig.3 Separation and correction of actual resistance

图3中,k(1)表示104档位;k(2)表示103档位;k(3)表示102档位;k(4)表示101档位;k(5)表示100档位;k(6)表示10-1档位;k(7)表示10-2档位。校正公式如下:

(4)

其中,数字7表示变阻箱的档位数,C0表示电路中固有的电阻。由于该电阻箱的精度为0.01 Ω,为了减少数值计算的舍入误差,对模型求解的结果sj进行误差分析及二次校正。其中,误差分析过程如下:对实际电阻值的校正值(模型的首次计算结果)sj进行档位拆分,阻值拆分公式如下:

(5)

以实际电阻的校正值sj=88 889.65 Ω为例,按照式(5)进行拆分,结果如下:

88 889.65=8×104+8×103+8×102+8×101

+9×100+6×10-1+5×10-2

如此便可以得到:

k′(1)=8,k′(2)=8,k′(3)=8,k′(4)=8,

k′(5)=9,k′(6)=6,k′(7)=5

将k′(i),i=1,…,7依照实际测量值g(j)计算首次校正值对应的实际电阻值sk,计算公式为:

(6)

此时,记Rk=|sc-sk|,表示首次校正值对应的实际电阻值sk与sc(要求的实际电阻值)之间的绝对误差。

1.5 二次校正

二次校正的具体过程如下:当|R|≤0.005时,说明校正结果在电阻箱的精度(0.01 Ω)要求范围内,符合要求,sk不需要进行二次校正;当R≤-0.005,说明校正结果偏大,超出了电阻箱的精度(0.01Ω)要求范围(正偏误差超过精度0.01),sk需要二次校正:sk=sk-0.01;当R≥0.005,说明校正结果偏小,超出了电阻箱的精度(0.01 Ω)要求范围(负偏误差超过精度0.01),sk需要二次校正:sk=sk+0.01。根据以上误差分析及二次校正过程设计了相应的算法流程,如图4所示。