基于动态Lloyd-Max 量化的网络化系统实时状态估计*

陈军勇

(浙江科技学院信息与电子工程学院，浙江 杭州 310023)

基于网络通信约束、信息量化与无线传输的系统状态估计与滤波是无线传感器网络(WSN)、网络化控制系统(NCS)等网络化系统应用中的共有基础性问题[1-3]。通常，系统状态估计与滤波作为整个网络化系统的基础部分，其往往有严格的实时(因果)性要求，甚至要求具备零延迟特性即每步的信源量化、编码、传输、解码与估计过程在一个时间步长内完成，这对整个系统的运行性能与稳定性起着关键性作用[4-5]。

针对一般性的马尔可夫信源实时编码与估计问题，Witsenhausen 和Walrand 等[6-7]较早地研究了其分别在无噪信道和有噪信道带无噪反馈环境下实时传输的编码器与解码器设计问题，建立了最优编码器与解码器的一些基本结构特征。进一步，Teneketzis 和Mahajan[8-9]研究了有噪信道且无反馈信息的马尔可夫信源实时传输最优设计问题，确立了有限时间平均失真测度最小化的最优实时编码与解码结构策略，同时提供了一种研究各种实时传输变体问题的统一方法。

对于线性动态系统的实时编码与估计问题，Nair 和Evans[10]证明基于编码观测信息的最优状态估计问题可以等价转换为马尔可夫信源的最优重构问题，然而其并没有提供具体的实现方案。此外，Nayyar 和Teneketzis[11]研究了多端通信系统的最优实时编码与解码函数设计问题，利用编解码两端的共有信息获得了时不变域的有限维充分统计量。Yüksel[12]针对部分观测马尔可夫信源的最优因果编码问题，证明了点对点通信下的估计-量化分离原理，但在多端通信系统中一般不存在类似的分离原理。

当前大部分相关文献研究了实时编码与估计系统的编解码理论最优结构问题，但多数都没有提供具体的设计与实现方案。由于系统的实时性限制和量化的非线性操作，其全局最优实现方案一般难以找到。针对线性动态系统，Msechu 等[13]基于状态预测分布的高斯近似，提出了一种分布式量化卡尔曼滤波算法，但其实现方案要求消息广播通道的存在，且缺乏编解码结构的最优性评估。基于类似的高斯分布近似，Leong 等[14]建立了多传感器观测下的线性量化滤波方案，且证明了算法在高率量化下的稳定性。近年，Stavrou 等[5]基于信息论导出了向量高斯-马尔可夫信源零延迟编码与估计的率失真性能上下界，且分析了点阵量化结合无记忆熵编码实现方案的率失真性能。

正如文献[12]所指出，对于动态系统的最优实时编码与估计问题，当前关键点是实时编码与估计的具体设计和实现方案，因此其也是本文的研究重点。本文主要针对线性离散动态系统，分析和简化了最优实时量化与估计结构的等效形式，并基于向量Lloyd-Max 量化原理和量化信源预测分布的高斯近似，设计了递推形式的动态Lloyd-Max 量化与估计实现算法，其中采用双边同步器利用发送端和接收端的共有信息实现了编解码操作的同步。本文主要贡献在于对最优实时量化与估计结构作出了一定优化，并提出了对应的实现方案与实现算法，仿真结果表明优于现有方案。最优实时量化与估计结构的简化以及所提出实现方案的递推运行特性，可使网络化系统节省大量存储空间并降低计算复杂度，这有利于保证系统的实时性和有效性，促进其在智能信息领域中的潜在应用。

1 问题描述

考虑图1 所示的网络化实时状态估计系统，其中动态系统状态由传感器进行实时观测，然后测量信息(集)通过一定方式的量化与编码，并经由无噪声无线数字信道发送至远程接收端，然后解码并估计出动态系统的实时状态。

图1 网络化实时状态估计系统

本文考虑如下所示的线性离散动态系统，其状态方程和观测方程描述为:

式中:系统状态Xk∈ℝp，初始状态X0～N(x0，M0)，系统矩阵A∈ℝp×p，驱动噪声Uk∈ℝp为独立零均值高斯随机序列，其协方差矩阵为Q。传感器观测Yk∈ℝq，观测矩阵H∈ℝq×p，观测噪声Vk∈ℝq为独立零均值高斯序列，其协方差矩阵为C。另外，{Uk，Vk}相互独立，且(A，H)可测。

本文要求网络化系统中量化编码与解码估计过程具有严格的实时性，即整个处理过程在一个时间步长内完成。设网络通道传输比特率为R位/bits，定义二进制量化输出为Zk∈ℤ ＝{0，1，…，2R-1}。不失一般性，对于发送端，在任意k≥1 时刻，其实时量化输出Zk可用如下量化函数表示，即:

式中:Fk(·)为实时量化函数，Y1:k＝{Y1，Y2，…，Yk}，Z1:k＝{Z1，Z2，…，Zk}。对于接收端，在每个时刻k，在保证实时性的前提下，解码/估计器可利用当前接收到的全部量化输出作出对当前系统状态Xk的最优估计，即:

式中:Sk(·)为实时估计函数。

我们采用均方误差(MSE)作为估计性能准则，定义K个时刻的估计MSE 之和为:

在本文中，我们主要研究如何设计最优实时量化与估计器，以极小化均方误差D(K)。注意到式(2)和式(3)所示的量化与估计函数要求发送端和接收端存储过去的所有观测数据或量化数据。对于资源受限的传感网络节点，当K较大或无限时，这将带来严重的存储负担，使得系统实现变得非常困难或不可实现。

针对上述问题，在保证估计性能最优化以及算法容易实现的前提下，本文首先需要对原始的实时量化与估计方式进行等价转换和优化，然后研究具体的实时量化与估计算法，并对其估计性能进行分析和评估。

2 量化与估计结构优化

本节讨论在没有任何估计性能损失的情况下，给出简化的最优实时量化与估计结构。

对于系统模型，根据标准卡尔曼滤波理论[15]，定义:

其分别为基于未量化观测Y1:k对状态Xk的最优MSE 估计和对应的误差协方差阵。

根据估计-量化分离原理[12]，本文优化问题可以等效转换为对标准卡尔曼滤波器输出的最优量化与重构问题，且代价函数式(4)可重写为:

根据标准卡尔曼滤波理论[15]，定义:

其分别表示基于未量化观测Y1:k-1对Xk的最优MSE 预测估计和对应的预测误差协方差阵。同时，Mk满足如下黎卡提方程:

式中:增益矩阵函数G(M)定义为:

Mk的收敛值M∞可通过求解如下渐近矩阵方程得到，即:

上述式(14)、式(15)和式(16)虽然给出了等效的最优实时量化与估计结构，但要获得具体的实时量化与估计实现方案并不容易。由于量化与估计操作的高度非线性，精确评估条件概率测度p(｜Z1:k-1)非常困难。因此，常用方式是作一定的分布近似，例如近似为高斯分布。由于高斯分布统计特性仅由均值和协方差描述，因此更容易寻求具体的实时量化与估计算法，且量化与估计操作只需额外存储有限个信息量，这使得整个网络化估计系统更易实现。

3 动态Lloyd-Max 量化与估计

本节首先介绍标量Lloyd-Max 量化器的基本原理，并导出高斯信源的量化基本特性。然后，基于标量Lloyd-Max 量化特性并在p(｜Z1:k-1)的高斯分布近似下，给出一种向量状态实时动态Lloyd-Max量化与估计实现方案。

3.1 标量Lloyd-Max 量化器

Lloyd-Max 量化器[16-17]是一种最小均方失真量化器。对于给定分布的连续随机信源x～p(x)，量化比特率为r位，量化规则如图2 所示，则量化输出:

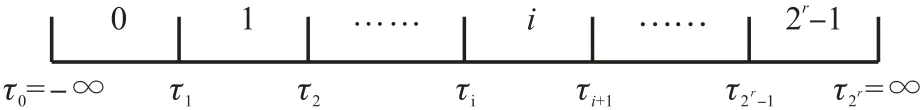
图2 量化器结构图

Lloyd-Max 量化器以分区质心为重构值，相邻重构值的中点为阈值，即重构值:

若随机信源x服从高斯分布，不失一般性，设x～N(0，1)，其概率密度函数用φ(x)表示，则易得:

且条件方差

3.2 动态Lloyd-Max 量化与估计实现方案

上节导出了标量高斯信源Lloyd-Max 量化器的一些基本特性，本节给出向量系统动态Lloyd-Max量化与估计的实时在线更新原理与递推实现方案。

根据贝叶斯最优估计原理[15]，有:

且估计误差协方差阵为:

量化误差协方差阵为:

同理，根据估计-量化分离原理[12]，可知:

为实现实时量化、编码与估计，系统运行时必须同步编码器与解码器。根据前述最优实时量化结构式(14)和式(15)，在任意时刻k，发送端和接收端可以基于过去的共有信息Z1:k-1得到编码器与解码器的同步规则。对于向量Lloyd-Max 量化器，我们需要获得量化信源预测分布p(｜Z1:k-1)。基于此，我们提出图3 所示的动态Lloyd-Max 量化与估计实现方案。在任意时刻k，首先运行标准卡尔曼滤波器得到状态估计，然后其经向量Lloyd-Max 量化与编码并发送到接收端，以解码并生成最终的最优状态估计。注意其中在发送端和接收端分别设置了同步器(双边同步器)，两者均基于过去的共有信息Z1:k-1获得一致的预测分布p(｜Z1:k-1)，以设计一致的向量Lloyd-Max 量化、编码与解码规则。

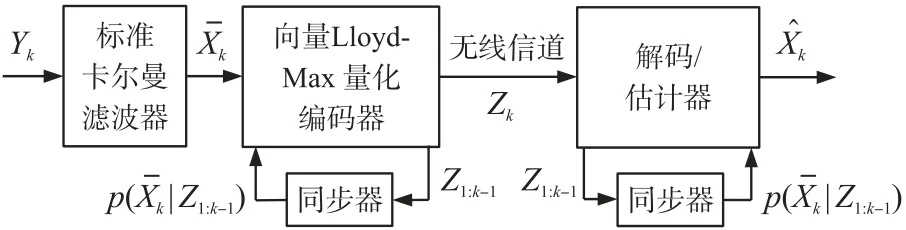
图3 动态Lloyd-Max 量化与估计实现方案

基于图3 所给出的实现方案，下面推导具体的向量Lloyd-Max 量化与估计及同步算法。如前所述，由于量化与估计操作的高度非线性，同步器精确实时评估p(｜Z1:k-1)非常困难，计算量相当大，不便于系统实现。因此，根据高斯-马尔可夫关系式(12)，我们可采用如下高斯分布近似，即:

相似的高斯近似参见文献[13-14]，数值结果显示该类近似具有较高的准确度和有效性，尤其对于高比特率量化，此时量化误差协方差阵Φk-1趋近于零，预测分布p(｜Z1:k-1)主要由高斯驱动噪声Δk决定。

前面我们给出了标量Lloyd-Max 量化器的一些基本特征，而对于向量源的量化，我们需要作一定变换。对任意时刻k，基于前面的高斯分布近似，在给定Z1:k-1下信源为多维相关高斯分布，因此根据最优向量量化原理[18]，可对其先作线性变换使其转换为分量独立高斯分布源，即:

分别采用p个独立的标量Lloyd-Max 量化器，其中(n)和(n)分别表示向量和的第n个分量。需要注意的是，在给定的量化比特率R位下，在的各分量之间存在一个最优量化比特分配方案以使总的量化均方误差最小。设rk(n)为分量(n)的量化比特率，则有。根据文献[18]，最优量化比特率满足如下条件，即:

接着寻找标准差最高的分量分配第二位，并按照式(34)进行修正，如此循环直至所有比特分配完毕。

由于系统中共存在p个独立的标量Lloyd-Max量化器，因此整个量化输出可表示为:

在任意时刻k给定Z1:k-1下，当接收端收到量化输出Zk，首先可根据式(20)和式(21)对归一化分量进行估计，对(n)的最优MSE 估计为:

且条件方差:

且条件方差:

且条件协方差矩阵:

式中:Cov(·)表示协方差阵。

最后，根据式(22)、式(28)和式(42)，对Xk的最优MSE 估计为":

且由量化误差协方差阵和式，有:

又由式(25)即可得估计误差协方差阵:

综上，式(44)和式(46)给出了关于Xk的实时最优MSE 估计及误差协方差阵的最终表示形式。

3.3 系统实现方案分析

对于本文提出的动态Lloyd-Max 量化与估计实现方案，整个系统运行过程由卡尔曼滤波、线性变换、比特分配、归一化、量化/编码、无线传输、解码/估计组成。由于对预测分布p(｜Z1:k-1)的高斯近似即式(26)和(27)，其均值Υk和协方差阵Ωk分别仅由前一时刻的估计-1和量化误差协方差阵Φk-1决定，因此整个动态量化与估计过程实际为一个递推过程，当前时刻的量化与估计操作仅与前一时刻的量化与估计结果有关，且在当前时间步长内完成，实现零步长延迟。量化与估计过程的递推运行也使整个网络化系统可以节省大量存储空间并减轻计算负担，确保系统的实时性和有效性。

4 仿真结果与分析

考虑如下的二维目标实时跟踪系统，其状态和观测方程描述为:

式中:状态向量Xk＝(sk，)T，sk和分别为目标位置和速度，T为采样周期，Uk为驱动噪声，Yk为传感器的观测量，Vk为观测噪声。

本文采用MATLAB 软件进行仿真，假定系统初始状态服从X0～N((0，5)T，0.2I2)，采样周期T＝0.1，驱动噪声Uk～N(0，2)，观测噪声Vk～N(0，1)。为简化，本文提出的动态Lloyd-Max 量化与估计算法用DLMQE 表示。仿真中全部MSE 结果通过105次独立模拟运行平均得到。

图4 给出了本文提出的DLMQE 算法在两种量化比特率下的理论和实际MSE 曲线以及其下界即标准卡尔曼滤波器(KF)的MSE。图4 中DLMQE和KF 的理论MSE 分别通过计算tr(＾Mk)的理论平均值和tr(Mk｜k)得到，而实际MSE 通过仿真过程中状态估计实际误差计算得到。

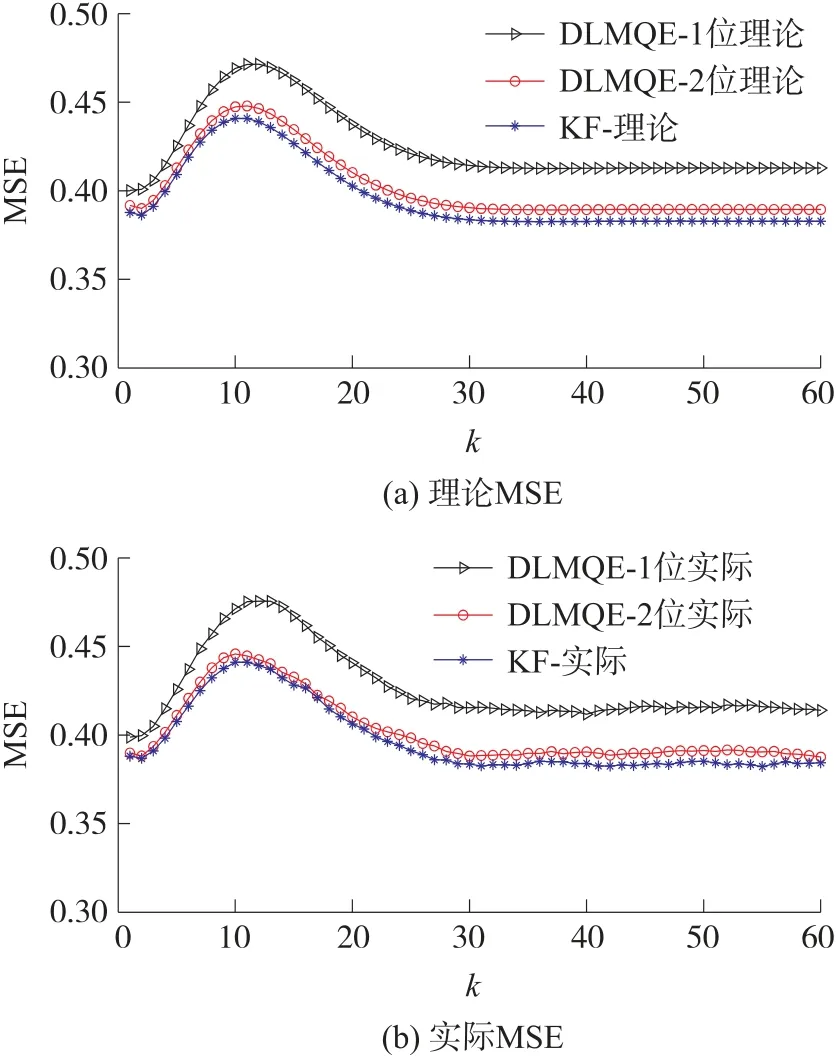
图4 DLMQE 理论和实际MSE 及其下界

从图4 可以看出，对于理论和实际MSE 曲线，其均随时间增加趋近于稳定，且量化比特率越大，DLMQE 算法估计性能亦越好。事实上，若量化比特率趋近于无穷大，则DLMQE 算法中量化误差将趋近于零，此时DLMQE 将完全等价于KF。

图5 给出了DLMQE 算法在不同量化比特率下的理论和实际MSE 曲线对比。从图5 可以看出，理论MSE 曲线和实际MSE 曲线非常接近，即使对于量化比特率仅为1 位的情形，两者之间也很好匹配。这反映了本文基于量化信源预测分布的高斯近似所提出的DLMQE 算法的有效性和准确性。

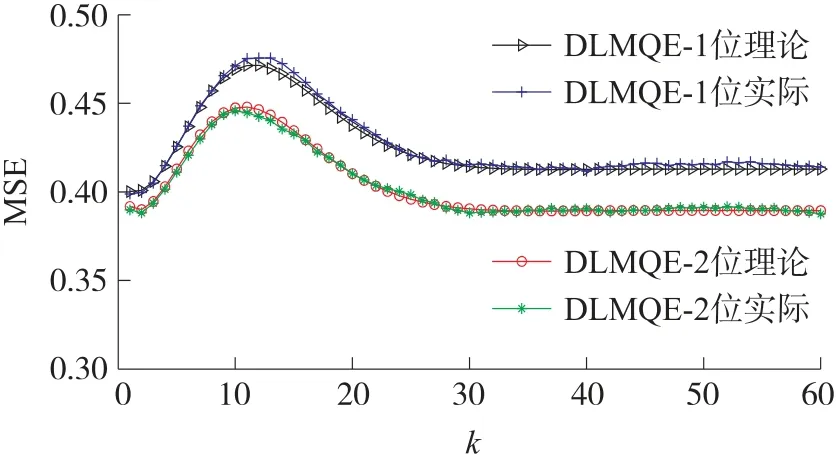
图5 DLMQE 理论和实际MSE 对比

进一步，为验证本文所提出算法的估计性能，定义如下渐近平均MSE 失真，即

对于无量化的标准卡尔曼滤波器，则有D∞＝M∞｜∞。

表1 给出了不同估计方案下的D∞数值计算结果。注意为进行性能对比，我们还计算了现有的量化卡尔曼滤波器(QKF)[13-14]的D∞值，其中量化的是观测新息而不是状态估计量，缺乏最优性。标准卡尔曼滤波器(KF)的D∞值也一并列出，其与量化比特率无关，作为所有量化估计器的D∞下界。

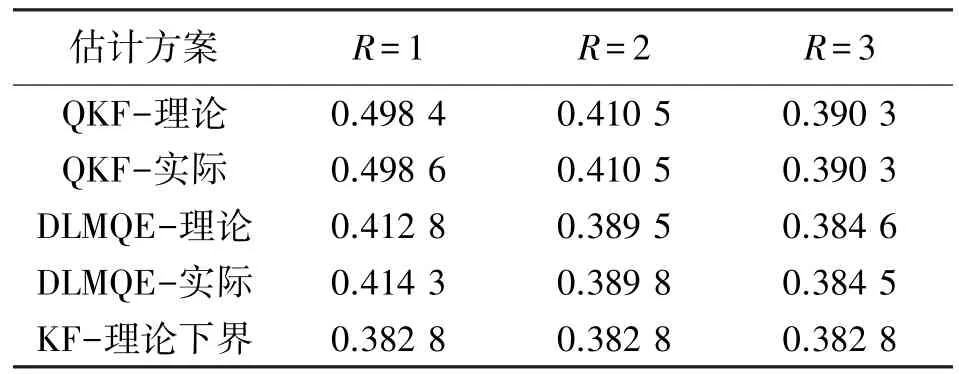
表1 渐近平均MSE 失真D∞比较

从表1 可以看出，随着量化比特率增加，DLMQE 和QKF 的D∞值均减小，即估计性能越好。在相同的量化比特率下，本文提出的DLMQE 的D∞值均小于现有的QKF，这说明了DLMQE 算法估计性能的优越性。此外，与图5 中的理论和实际MSE曲线对比结果类似，从表1 中的数值结果亦可以看出D∞的理论值和实际值非常接近，即使对于低比特率区域。这进一步证实了对量化信源预测分布进行高斯近似的有效性和准确性。

5 结论

本文研究了网络化线性离散动态系统的最优实时量化与估计问题。根据估计-量化分离原理，原优化问题可以等效转换为一阶高斯-马尔可夫信源的最优量化与重构问题，进而分析了最优实时量化与估计结构的等效简化形式。然后，基于Lloyd-Max量化原理和量化信源预测分布的高斯近似，设计了递推形式的向量动态Lloyd-Max 量化与估计实现方案，其中采用双边同步器利用发送端和接收端的共有信息实现了编解码操作的同步。最优实时量化与估计结构的简化以及方案实现过程的递推运行，使系统可以节省大量存储空间并降低计算复杂度，有利于保证系统的实时性和有效性。MATLAB 仿真结果表明，本文提出的动态Lloyd-Max 量化与估计算法(DLMQE)估计性能优于现有的量化卡尔曼滤波器(QKF)，且即使对于较低的量化比特率区域，DLMQE 算法依然有效。