非视距环境下基于TOA 的移动目标定位
2024-01-09张晨,王刚
张 晨,王 刚
(宁波大学信息科学与工程学院,浙江 宁波 315211)
目标定位在近几年来一直是研究热点,也是无线传感网络(Wireless Sensor Networks,WSN)的重要任务。移动目标定位作为其中的一部分,在物流管理、车辆导航和紧急救援等领域都有着重要的应用[1-4]。
在移动目标定位场景中,传感器采集目标发射电磁波的时间信息或频率信息。常见的时间测量信息有:到达时间(Time-of-Arrival,TOA)[5-6]和到达时间差(Time-Difference-of-Arrival,TDOA)[7-10];常见的频率测量信息有:到达频率(Frequency-of-Arrival,FOA)[5-6]和到达频率差(Frequency-Difference-of-Arrival,FDOA)[7-8]。其中频率测量依赖于物体的位置,加上物体移动速度未知,频率测量比时间测量更加复杂[11],因此本文采用时间测量的方法,它比频率测量更加直接。定位的精度是需要关心问题,已有文献讨论基于时间测量的移动目标定位问题[12-14],且取得了良好性能。但在实际的定位环境中,如城市中心,由于障碍物的遮挡,移动目标发射的电磁波往往需要经过多次反射或衍射才能到达锚节点,即传播路径是非视距的(Non-Line-of-Sight,NLOS)。在这种情况下,非视距传播所引起的误差对定位精度会产生很大的负面影响,而且已有文献表明,非视距误差通常远大于测量噪声[15]。此外,由于定位环境的不断变化,所以非视距误差的统计信息难以获得,因此减少非视距误差的影响在移动定位中就显得格外重要。
对于非视距误差的处理,已有很多文献对其进行了研讨。例如文献[16-17]使用非视距误差的统计信息来提高定位精度,但是在实际环境中,统计信息往往难以获得。针对这种情况,文献[15,18-21]提出了不需要已知非视距误差的统计信息和路径状态的方法。一种是采用鲁棒处理的方法,文献[18]提出对非视距误差做鲁棒处理,将其转化为最大最小问题,再利用二阶锥松弛(Second-Order Cone Relaxation,SOCR) 和半正定松弛(Semidefinite Relaxation,SDR)技术对其进行处理。这种方法仅要求已知非视距的误差上界。然而,当测量环境为视距时,已知的上界通常太大,导致这种方法在稀疏非视距环境中没有很好的性能。另一种是采用估计处理的方法,文献[15]提出了联合估计源位置和与非视距误差有关的平衡参数的方法,并通过SOCR和SDR 对问题进行松弛,从而缓解了非视距误差的影响。文献[19]提出了非视距环境下协作定位,对源位置和非视距差的二次多项式进行估计,并通过SDR 对问题进行松弛。而文献[20-21]采用估计处理和鲁棒处理结合的方法,联合估计源位置和与非视距误差有关平衡参数,同时对新的变量做鲁棒性处理。在估计的方法中,若直接对所有的非视距误差进行估计,会涉及到大量的优化变量,意味着需要大量的精确测量来估计所有的参数,这在密集的非视距环境下,会由于测量不精确导致性能下降[20]。
本文研究了非视距环境下基于TOA 的移动目标定位问题。WSN 中的锚节点对移动目标进行多次采样得到多组TOA 测量值,每组均含有测量噪声和非视距误差。对测量数据采用估计的方法,但如果直接估计移动目标的初始位置、移动速度和所有的非视距误差,在采样点多的情况下,模型会涉及到大量的优化变量,从而导致精度下降。因此对于非视距误差不进行直接估计,参考文献[19]的方法,将非视距误差的一次项和二次项进行组合,再加上合理的近似,对其整体进行估计,这样优化变量的数目便可减少。接着在此基础上,推导出约束最小二乘(Least Squares,LS)问题,这是一个非凸的问题,通过SDR 将其松弛为凸的SDP 问题,该方法不需要知道非视距误差上限和路径状态。通过对算法的仿真与分析,发现在密集和稀疏的非视距的环境下,本文提出的方法都取得了良好的性能,从而有效减轻了非视距误差产生的负面影响。
本文的章节内容组织如下。第一节描述了基于TOA 的移动目标定位场景;第二节详细阐述了构造约束LS 问题并将其松弛为凸的SDP 问题的推导过程;第三节通过仿真给出了算法的性能分析并探究了惩罚因子对算法敏感度的影响;第四节给出结论。
文本采用的符号说明如下。向量和矩阵分别用粗体小写字母和粗体大写字母表示。ai表示向量a中第i个元素;A(i,j)表示矩阵A中第(i,j)个元素。a(1:i)表示向量a中第1 到第i个元素所构成的子向量;A(1:i,1:j)表示矩阵A中第1 到第i行,第1 到第j列所构成的子矩阵。0k×l代表k行l列的全零矩阵。tr(A)和rank(A)分别表示矩阵A的迹和秩;A≥0表示矩阵A是半正定的。ℝk表示k维实空间。
1 问题描述
考虑一个k(k=2 或3)维场景上的移动目标定位问题。如图1 所示,设WSN 中有N个已知的锚节点和1 个未知的移动目标,其中第i个锚节点的坐标用si∈ℝk(i=1,2,…,N)表示,移动目标初始位置的坐标用x∈ℝk表示,移动速度用v∈ℝk表示,每个锚节点对移动目标的采样点数为M,且采样周期为T。假设T的数值很小,则可以认为移动目标在整个过程中速度保持不变[21]。
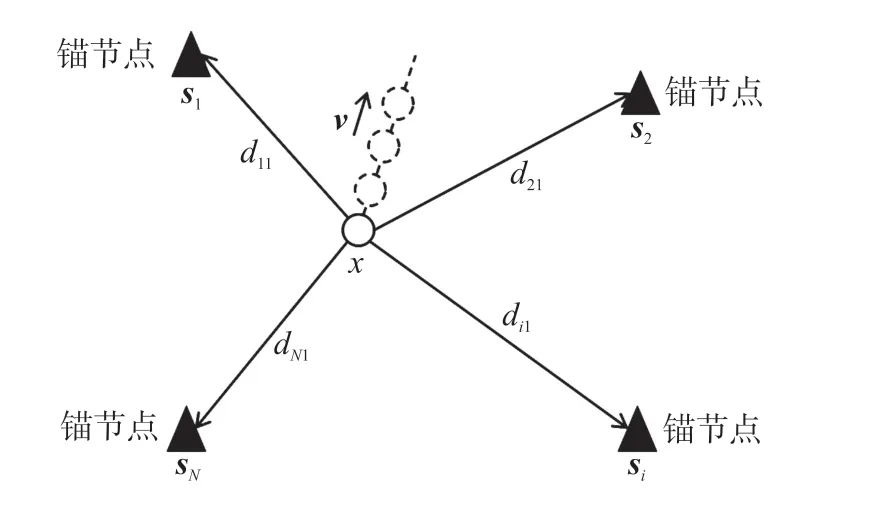
图1 移动目标定位场景
设锚节点和移动目标之间存在着测量噪声和非视距误差,则相应的TOA 测量模型如下所示:
式中:c是光速,nij/c是第i条路径上进行第j次采样时的测量噪声。假设T的数值很小,则锚节点和移动目标之间的信号传播路径基本不变,于是可以认为锚节点M次采样时的非视距误差均相等,于是用ei/c来代表第i条路径上每次采样到的非视距误差。将式(1)两端同时乘以c,则相应的测量模型转化为如下所示:
通常假设nij是服从均值为零,方差为的高斯分布。ei是取值为正的非视距误差,由于真实环境在不断变化,所以它的分布往往难以获得,通常只假设它的上限为ρi,即0≤ei≤ρi。这里还要指出,测量噪声往往比非视距误差小很多,即ei≫nij,从而非视距误差在移动目标定位中需要格外关注[15]。
2 半正定规划问题的构造
在本节中,首先在式(2)的基础上推导并构造出约束LS 问题,然后对其进行松弛,转化为易于处理的凸的SDP 问题,从而完成对移动目标的初始位置和移动速度的估计。
首先将式(2)中的ei移到等式左边,并对等式两端进行平方,得到的结果如下所示:
对式(3)的两端展开并移项,可得:
式中:测量噪声的二次平方项被忽略,因为其数值上远小于‖x+jTv-si‖2[15],而非视距误差的二次项不能被忽略。
对于非视距误差的处理,采用估计的方法。式(4)中含有非视距误差的一次项2dijei和二次项。为了减少优化变量的数目,在T不大的情况下,非视距误差一次项中的dij可以近似用第i条路径M次采样的平均值来代替:
令ci=2ei-(i=1,2,…,N),即用ci代替非视距误差一次项和二次项的整体,则对非视距误差的估计转化为了对ci(i=1,2,…,N)的估计。本文将ci作为变量与移动目标初始位置x和移动速度v进行联合估计。由此定义,式(4)可转化为:
进一步,令u=‖x‖2,w=‖v‖2,z=xTv。并且令c=[c1,c2,…,cN]T,则式(6)可写为:
根据式(8),可以构造如下约束LS 问题:
问题(10)仍是一个非凸问题,难以求解。本文通过SDR 将其松弛为SDP 问题。为此,引入矩阵Y并令Y=yyT,则约束(10a)-(10c)分别可以表示成如下形式:
则问题(10)可以转化为:
通过引入:
再结合如下的等价变换:
则问题(12)可以转化为:
在问题(15)中,唯一的非凸约束是rank(Y)=1这一项,将其舍弃,则问题(15)可以转化为如下凸的SDP 问题:
为了使松弛后的SDP 问题更加收紧于原问题,需要引入一些额外的约束项。注意到:
因为nij≪‖x+jTv-si‖,且ei≥0,所以容易得到ci≥0,并且有如下的等价表示:
于是本文在问题(16)中引入约束(18)来进行收紧。而且为了避免问题(16)中ci的解太大,我们对其增加一个惩罚项来抑制ci的值。于是得到最终凸的SDP 问题:
式中:λ为惩罚因子。求解问题(19),便可以得到移动目标的初始位置估计和移动速度估计。本节最后给出算法的伪代码,用来总结所提出的方法,具体如算法1 所示。

算法1 移动目标定位的SDP 算法
3 仿真与分析
3.1 算法复杂度分析
通常解决混合SDP/SOCP 问题的复杂度为:
式中:m是等式约束的个数,NSD和NSOC分别是半正定锥约束和二阶锥约束的个数,分别是第i个半正定锥和二阶锥的维度,μ=为壁垒参数,用来测量所涉及锥的几何复杂度,ε>0是解的精确度。下文用“SDP-NLOS”来指代本文所提出的方法,该方法有4 个等式约束[(11a) -(11c),(18)],有1 个维度为2k+N+4 的半正定锥约束[(15a)],二阶锥约束的个数和维度均为零,所以SDP-NLOS 最坏情况下的复杂度为O[4(2k+N+4)3.5ln(1/ε)]。为了和文本提出的方法形成对比,文章综合文献[20-21]对非视距误差的处理方法:鲁棒处理和估计处理结合的方法,并将其拓展到移动目标定位问题上,且将其命名为“RSDP”(鲁棒SDP),具体推导过程见附录。该方法有NM+4 个等式约束[(34b),(38e),(38f)],有3 个半正定约束[(33),(38a),(38b)],维度分别为NM+1、2k+1 和NM+2,二阶锥约束的个数和维度均为零,所以RSDP 最坏情况下的复杂度为O[(NM+2)4.5ln(1/ε)],可以发现,本文提出算法的复杂度明显低于RSDP,且随着采样点数的增加,这种效果更加明显。
3.2 仿真结果
在本小节中,通过软件仿真对本文所提出的方法进行性能测试与分析。为了进一步体现SDPNLOS 对非视距误差的缓解作用,本文在问题(19)的基础上舍弃非视距误差的一次项2dijei和二次项,得到不考虑非视距误差的SDP 问题:
矩阵A、B和常数r的形式同(13a)-(13c),下文将该算法命名为“SDP”。
为了对比分析SDP-NLOS、SDP 和RSDP 的定位性能。本文通过MATLAB R2017a 软件进行仿真,求解工具箱采用CVX,求解器为Sedumi。首先设置维数k=2,采样周期T=0.6 s,SDP-NLOS 中惩罚因子λ=0.1,并且根据文献[20-21],设置RSDP 中的取ρij平均值的一半,即:
然后在表1 中给出各个锚节点的坐标。
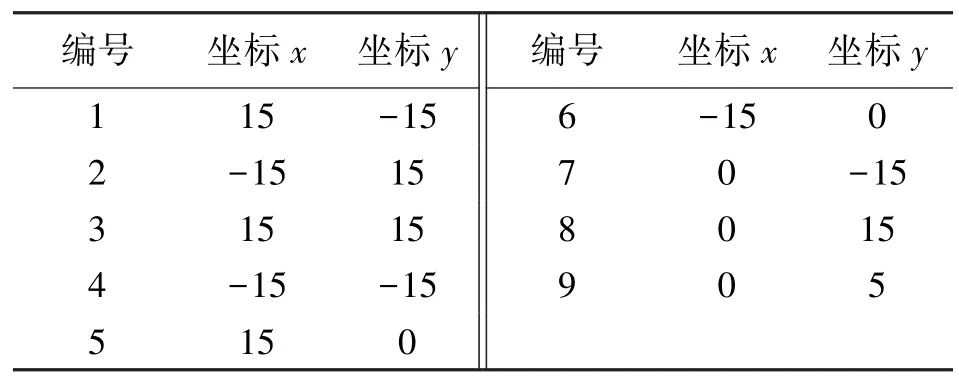
表1 锚节点坐标
移动目标在[-25 m,25 m]×[-25 m,25 m]的正方形区域内随机产生50 个,而且每个移动目标x轴方向的移动速度vx和y轴方向的移动速度vy均在-2 m/s~2 m/s 之间随机产生。最后根据式(2)生成含噪声的TOA 测量值,其中测量噪声由高斯分布产生,令=σ2,则nij~N(0,σ2),其中非视距误差由均匀分布产生,令ρi=ρ,则ei~U(0,ρ)。
移动目标的定位性能用均方根误差(Root Mean Square Error,RMSE)来衡量。对初始位置x估计的RMSE 和对移动速度v估计的RMSE 分别定义为:
式中:和分别是估计出的初始位置和移动速度,xi和vi分别是真实的初始位置和移动速度,M为蒙特卡洛仿真次数,设置每个移动目标仿真500次,又因为有50 个移动目标,所以M=25 000。下文考虑五种仿真场景,在场景一到四中,每条路径状态(视距或非视距)都是随机选取的,且每条路径属于非视距的概率均设置为50%[20-21]。需要指出的是,RSDP 需要知道非视距误差的上限,而SDP-NLOS和SDP 不需要知道误差的上限。
场景一:改变非视距误差上限ρ=1,2,…,6,考虑非视距误差对移动目标定位的影响。设置锚节点的个数N=5,编号为1~5,每个锚节点的采样点数M=4,测量噪声的标准差σ=0.1。初始位置估计的仿真结果如图2(a)所示,移动速度估计的仿真结果如2(b)所示。能够发现随着非视距误差上限的增加,三种方法对于移动目标的定位性能均有所下降,其中SDP-NLOS 与RSDP 相比,在移动速度的估计上没有明显的差异,但在初始位置的估计上有着明显的优势。具体地,当ρ=6 时,SDP-NLOS 和RSDP相比在初始位置的估计上有0.3 m 左右的优势。由于SDP 未考虑非视距误差的影响,因此SDP 对于位置和速度的估计均是最差的。综合分析,本文提出的方法SDP-NLOS 更有优势。
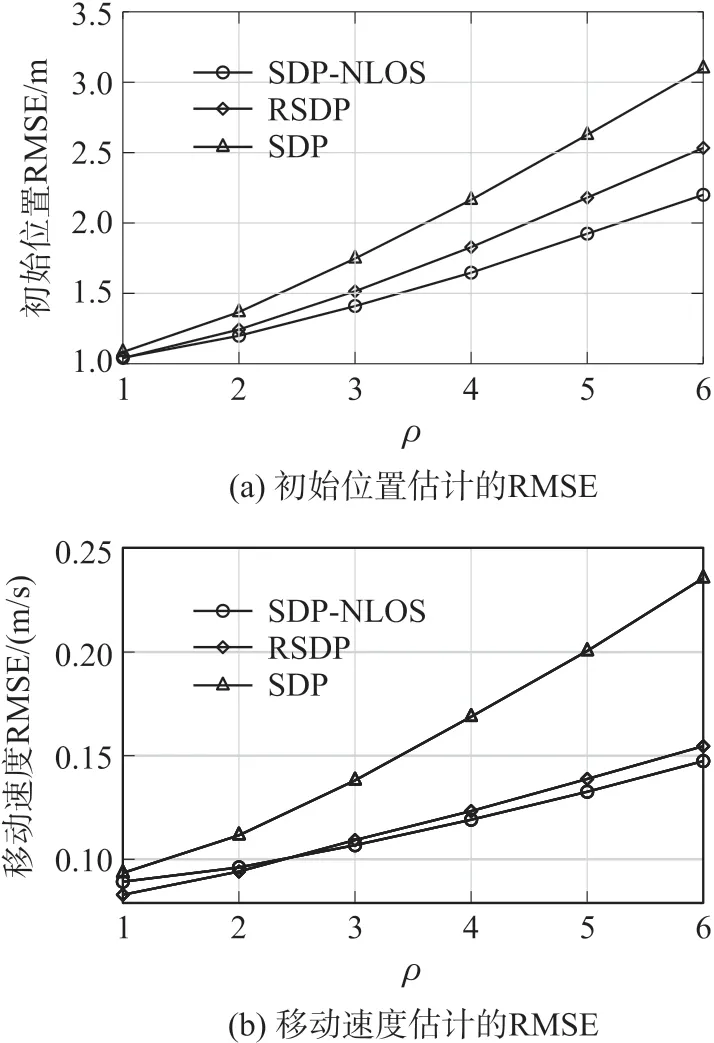
图2 非视距误差上限变化时的性能比较
场景二:改变测量噪声的标准差σ=0.1,0.2,…,0.6,考虑测量噪声标准差对移动目标定位的影响。设置锚节点的个数N=5,编号为1~5,非视距误差上限ρ=5,每个锚节点的采样点数M=4。初始位置估计的仿真结果如图3(a)所示,移动速度估计的仿真结果如图3(b)所示。能够发现,随着噪声标准差的增加,三种方法对于移动目标的定位性能均有所下降,SDP-NLOS 与RSDP 相比,在移动速度的估计上有平均0.03 m/s 的劣势,但在初始位置的估计上有平均0.23 m 的优势。而SDP 对于两者的估计是最差的。综合位置和速度的分析,本文提出的方法SDP-NLOS 更具有优势。
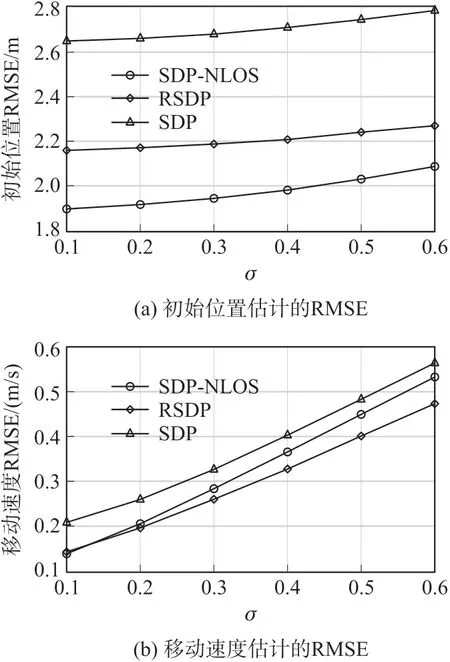
图3 噪声标准差变化时的性能比较
场景三:改变锚节点个数N=4,5,…,9,考虑锚节点个数对移动目标定位的影响。设置非视距误差上限ρ=5,测量噪声的标准差σ=0.1,每个锚节点的采样点数M=4。初始位置估计的仿真结果如图4(a)所示,移动速度估计的仿真结果如图4(b)所示。能够发现,随着锚节点个数的增加,三种方法对于初始位置和移动速度估计的RMSE 均有所下降,这是因为随着锚节点个数的增多,获取到的信息会增多,对位置和速度估计的精度就会提高。其中SDP-NLOS 对两者估计的性能最优,RSDP 的性能次之,SDP 的性能最差。

图4 锚节点个数变化时的性能比较
场景四:改变采样点数M=2,3,…,7,考虑采样点数对移动目标定位的影响。设置锚节点的个数N=5,编号为1~5,非视距误差上限ρ=5,测量噪声的标准差σ=0.1。初始位置估计的仿真结果如图5(a)所示,移动速度估计的仿真结果如图5(b)所示。能够发现,随着采样点数的增加,提出的方法对于移动目标的定位性能提高,这是由于当采样点数增加时,相应得到的方程数就会增加,对位置和速度估计的精度就会提高。其中SDP-NLOS 更占有优势。具体地,SDP-NLOS 和RSDP 相比,在初始位置的估计上有平均0.32 m 的优势,在移动速度的估计上两者无明显差别。同样地,SDP 对于两者的估计是最差的。
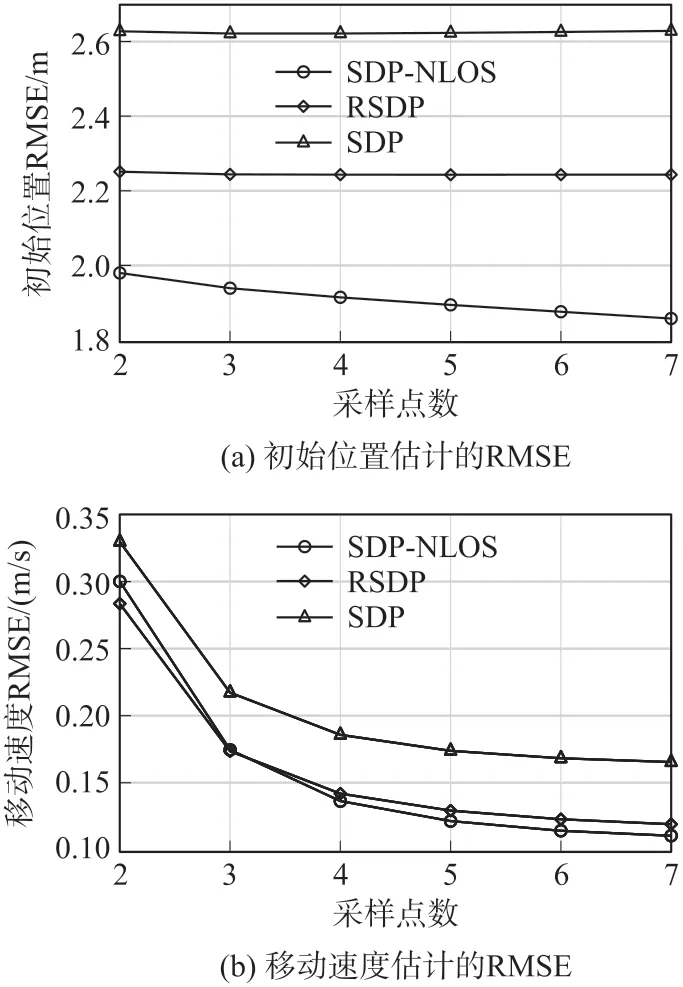
图5 采样点数变化时的性能比较
场景五:通过改变非视距路径的个数Nnlos=0,1,…,5,考虑路径状态对移动目标定位的影响。设置锚节点的个数N=5,编号为1~5,每个锚节点的采样点数M=4,非视距误差上限ρ=5,测量噪声的标准差σ=0.1。初始位置估计的仿真结果如图6(a)所示,移动速度估计的仿真结果如图6(b)所示。具体地,当所有路径均为非视距时,由于RSDP 做了鲁棒性处理,因此性能优于提出的方法SDP-NLOS,但当视距路径的比例大于1/5 时,SDP-NLOS 的性能优于RSDP;由于SDP 未考虑非视距误差的影响,因此SDP对于两者的估计在大多数情况下是最差的。可以发现,本文提出的方法SDP-NLOS 能应用于视距和非视距同时存在的场景,且定位效果良好。
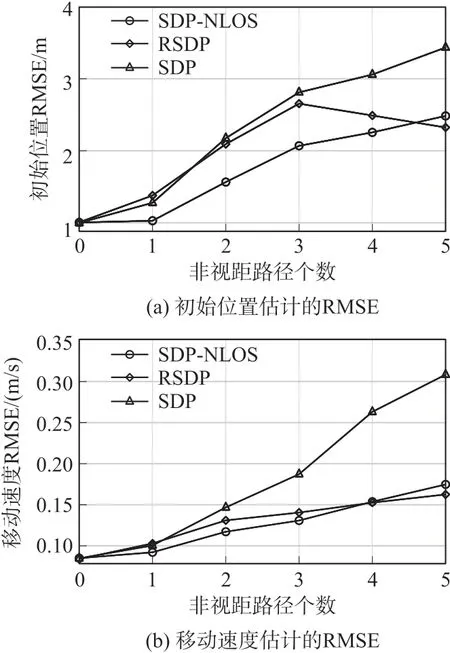
图6 非视距路径的个数变化时的性能比较
3.3 惩罚因子对算法敏感度的影响
通过改变惩罚因子λ,来观察不同的λ对SDPNLOS 敏感度的影响,这样能在实际的场景下,为λ的选取提供参考。设置锚节点的个数N=5,编号为1~5,每个锚节点的采样点数M=4,非视距误差上限ρ=2,测量噪声的标准差σ=0.1。在此场景下改变λ,得到的结果如图7 所示。可以发现当λ≥0.01时,对初始位置估计的RMSE 大约在1.23 m~1.38 m之间,波动幅度不大。而对移动速度估计的RMSE 大约稳定在0.098 m/s 左右,基本无变化。因此该方法对λ变动的敏感度较低,从而使λ的选取有着较大的范围。
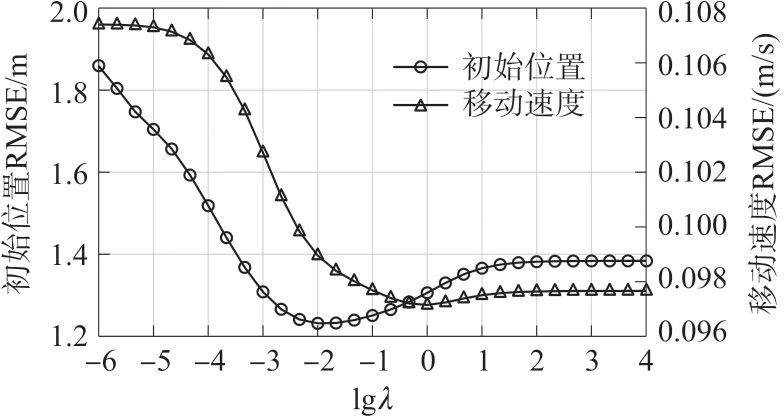
图7 惩罚因子λ 变化时,初始位置估计的RMSE变化和移动速度估计的RMSE 变化
4 总结
本文基于TOA 的测量方法研究了非视距环境下移动目标的定位问题。为降低非视距误差的影响,本文采用估计的方法,构造了约束LS 问题,实现了对移动目标的初始位置、移动速度和非视距误差的联合估计。并通过合理的近似,使优化变量的数目得以减少,以增加模型求解的准确程度。本文对该问题进行松弛,转化为了凸的SDP 问题,并通过仿真证实了该方法在稀疏和密集的非视距环境下均有着良好的性能。本文提出的方法不需要知道非视距误差上限,且在算法复杂度上有着明显的优势。
附录 RSDP(鲁棒SDP)的推导
文章综合文献[20-21]对非视距误差的处理方法,并将其拓展到非合作式移动目标定位问题上。
针对移动目标的距离测量值可以写成下式所示:
根据式(26),有如下的鲁棒约束最小二乘问题,其中对目标位置x,移动速度v和平衡参数做估计处理,对产生新的变量做鲁棒处理:
将问题(28)写成上镜图的形式:
通过S-Lemma,式(30)可以转化为存在λ≥0使得:
则问题(29)可以转化为如下所示:
问题(34)仍是一个非凸问题,难以求解。下面通过SDR 将其松弛为SDP 问题。为此引入矩阵G并令G=ggT,引入向量y=[xT,vT]T∈ℝ2k和矩阵Y,并令Y=yyT,则q可以表示为:
再结合如下的等价变换:
则问题(34)可以转化为如下的SDP 问题:
在问题(38)中,非凸约束是矩阵的秩等于1 的约束,现将其舍弃,则问题(38)最终可以转化为如下凸的SDP 问题:
综上所述,问题(39)便是综合文献[20-21]后产生的非合作式移动目标定位问题,即正文中的RSDP(鲁棒SDP)方法。
