地下水流影响下含盐饱和粉砂地层中联络通道冻结温度场的特征分析

李 飞, 王长虹, 张海东, 董济涵

(上海大学力学与工程科学学院, 上海 200444)

人工地面冻结法是将土体周围地层冻结, 加固土体、隔绝地下水, 并把对邻近构筑物的影响降低到最小程度的一种工法, 已被广泛应用于地铁工程[1-6].地铁联络通道施工是地铁建设的薄弱环节, 常处于复杂的地质环境, 如在沿海地区修建地铁联络通道, 存在水流和盐分等不利地质条件, 既要考虑联络通道本身的安全, 又要考虑对周边建筑物的影响, 若处理不当势必引起严重的工程事故.

关于冻结过程中的多场耦合分析已经有了很多研究成果.在理论和数值模拟方面,Harlan[7]基于非饱和土中水分迁移与冻结土层中未冻水的水分迁移理论, 提出了水-热耦合概念.Lai 等[8]研究了饱和粉土水-热-力相互作用过程的理论模型.Grenier 等[9]研究了冻融系统的地下水流动和热交换.岳汉森[10]在Harlan 模型的基础上, 考虑土体冻融过程中盐分的对流和扩散作用, 建立了水-热-盐耦合运移数学模型.赖远明等[11]根据传热学、渗流理论及冻土力学提出了考虑相变的温度场、渗流场和应力场耦合问题的数学模型及其控制方程, 并应用于岩土工程.肖泽岸等[12]建立了含氯化钠盐土层冻结过程中水-盐迁移及变形的计算模型, 该模型反映了含盐土体层在冻结过程中的温度、水分、盐分及变形规律.Xu 等[13]考虑溶质的扩散与对流, 基于Darcy 渗流定律、能量守恒定律和Fick 扩散定律提出了盐渍土的水-热-盐耦合方程.

在室内试验方面, Pimentel 等[14]在渗流条件下开展了人工冻结土的大型室内试验研究.邴慧等[15]通过对青藏铁路沿线不同土质在不同含盐量和含水量下的冻结温度试验, 得出土层冻结温度随含盐量的增加而降低, 随含水量的增加而升高的结论.孙立强等[16]通过室内试验得出了土体热物理参数随温度场的变化规律.

在现场监测方面, 林萍等[17]以上海长江隧道的联络通道为工程背景, 提出了一种冻土压力的现场监测方法.苏文德[18]针对国内首条海底地铁隧道的冻结法展开研究, 揭示了海底隧道联络通道冻结温度场的变化规律.Yan 等[19]采用现场监测、理论解析和数值模拟相结合的方法, 分析了广州地铁3 号线联络通道的冻结壁厚度与平均温度.郜新军等[20]基于现场试验,对饱和粉质黏土地层联络通道冻结法施工中的温度场变化进行了研究, 对温度、冻结壁、冻胀和地表沉降的发展规律展开了分析.

上述研究从基础理论、数值计算、室内试验和现场监测等方面对冻结法进行了总结, 对冻结法的温度场、渗流场和盐分场随时间的变化进行了深入分析.但类似南通地铁联络通道冻结法在地下水流-盐分共同作用下的机理尚不明确.为此, 本工作以南通城市轨道交通1 号线永兴大道站—深南路站区间4#联络通道工程为背景展开研究.首先, 建立了水-热-盐三场耦合的物理数学方程; 然后, 利用有限元软件COMSOL Multiphysics 模拟含盐土体的冻结模型试验,并分析对比试验结果; 最后, 基于背景工程的特点, 开发了多物理场数据监测设备, 对比分析监测数据与三场耦合模拟数据.

1 控制方程

为了研究含盐土层在人工冻结过程中的水-盐迁移和水-冰相变过程, 考虑水流影响, 建立水-热-盐三场耦合方程.引入以下假设: ①土体骨架和冰晶体不可压缩; ②土体为各向同性的均匀介质; ③水分在迁移的过程中符合Darcy 定律.

1.1 相变温度与未冻水含量

盐分的存在降低了含盐地下水的冻结温度, 进而影响土层的冻结过程.通过Clausius-Clapeyron 方程可得到相变温度的降低幅度.通过适当简化, 冻结温度Tf的变化[21]为

式中:Tf为土体冻结温度(K);T0为纯水冻结温度(K);R是气体常数,为8.314(J·mol-1·K-1);ρw为水的密度(kg/m3);L为水-冰相变时释放的潜热值(kJ/kg);c为盐分浓度(mol/L).含盐土体层的冻结温度Tf也可以表示为

在孔隙溶液中, 如果有盐分的存在, 不仅会影响土体冻结温度, 还会影响溶液的成分.在不含盐分的土体层中, 孔隙中未冻水的饱和度Sw0[9]为

式中:Sr为残余含水量;W为与土性有关的参数.

当土体层含有盐分时, 含盐孔隙溶液的饱和度Sl[12]为

式中:A1,A2和A3是与土性有关的系数;M,m是与孔隙有关的系数.

孔隙中未冻水的饱和度为

式中:Vϕ为盐分的表观摩尔体积.

1.2 水分场控制方程

水分的变化符合Darcy 定律, 根据质量守恒定律, 孔隙溶液中水分的质量变化[9]表示为

式中:n为孔隙率;Si,Sw分别为冰和水的饱和度,Si+Sl= 1;U是水流速度,U=Kw为渗透系数.随着温度的降低, 冰晶将堵塞孔隙, 导致土体的渗透性降低, 则孔隙溶液中土体的渗透系数[22]为

式中: flc2hs 为平滑的Heaviside 函数;δT为相变区间;kr为残余渗透系数.不考虑冰晶的压缩性, 式(6) 可以表示为

考虑水的压缩性, 引入水的压缩系数[9]

则式(8) 可以表示为

当溶液为稀溶液时, 浓度对未冻水含量的影响很小,Sl可以表示为未冻水的含量, 则水分场的控制方程可以简化为

1.3 温度场控制方程

在传热过程中, 热传递包括3 个方面, 分别为热传导、热对流和热辐射.由于地下水的流动, 对流所引起的热传递不可忽略, 地下水流速度越快, 对传热的影响就会越大.热辐射的量很小, 可以忽略不计.此外, 水-冰相变将释放大量的潜热, 能量守恒方程除了热传导和热对流, 还包括相变项.温度场的能量平衡方程[9]为

式中:ρs、ρl和ρi分别为土体骨架、孔隙溶液和冰晶的密度, kg/m3;Cs、Cl和Ci分别为土体骨架、孔隙溶液和冰晶的比热容, J/(m3·K);λs、λl和λi分为别为土体骨架、孔隙溶液和冰晶的热传导系数, W/(m·K).

1.4 盐分场控制方程

土体中溶质的运移包括3 种方式, 分别为对流、分子扩散和机械弥散[23].在含盐地下水的流动过程中, 主要涉及对流和分子扩散.盐分的变化主要来源于两个方面, 一方面是对流引起的盐分迁移, 对流指的是盐分溶解于液态水中而迁移的过程, 在冻结过程中, 主要指的是未冻水在流动过程中引起盐分的变化; 另一方面是分子扩散引起的盐分迁移, 分子扩散指的是溶液中溶质分子的热运动, 可在浓度梯度的条件下发生, 不受溶质分子运动的制约.根据质量守恒定律, 盐分场的迁移方程[12]为

式中:Ms为溶质的相对分子质量;D为溶质的扩散系数(m2/s),D=D0Slξ,D0为溶质在未冻区的扩散系数.

2 多场耦合分析验证

参考经典的盐渍土冻结模型试验, 下面采用数值计算方法模拟冻结模型试验, 对比分析模拟结果与试验数据, 验证多场耦合分析方法的有效性.

2.1 模型试验

应赛等[24]在盐渍土冻结过程温度变化的研究中, 对土样在不同浓度下进行了室内冻结模型试验.如图1 所示, 将高35 mm, 直径35 mm 的土样放入金属容器中, 采用低温冷浴控制装置对土样进行降温冻结.将温度探头插入金属容器内的土样, 冷浴温度由18◦C 降到-15◦C,土样的降温速率为(0.3±0.05)◦C/min, 顶板为绝热材料.

使用COMSOL Multiphysics 有限元软件自定义偏微分方程模块求解土样在不同盐分浓度下, 温度随时间的变化规律.在多场耦合分析中, 土样的盐分浓度分别取0、0.076、0.305 和0.609 mol/L.通过数值计算验证土样冻结温度和冻结过程随盐分的变化规律.

2.2 模拟与试验结果对比分析

土样在不同盐分浓度条件下的模型试验结果如图2 所示.盐分浓度越高, 土样降温冻结至-15◦C 所需的时间越长.冻结过程经历4 个阶段: 第一阶段为过冷阶段, 孔隙溶液没有开始转化成冰, 此时的最低温度称为过冷温度, 也是冰开始产生的温度; 第二阶段为上升阶段, 大量冰开始产生, 释放大量潜热, 土样温度略微回升; 第三阶段为稳定阶段, 冰水相变所释放的潜热与外界交换热量相平衡, 温度不变; 第四阶段为下降阶段, 当土体中的自由水大部分形成冰后,将不会产生潜热, 因此土体温度快速下降.在冻结前期, 不同盐分的土样之间温度变化不明显,这是因为冻结前期并没有形成冰, 盐分主要对土体冻结温度产生影响.数值模拟结果和模型试验数据契合度较高, 误差在0.5◦C 之内.

图2 不同盐分浓度下温度随时间的变化Fig.2 Temperature variation over time at different salt concentrations

利用有限元软件COMSOL Multiphysics 多场耦合分析方法能够有效模拟含盐土体的冻结过程.已有研究[9,25]中, 含有水头的人工冻结法的模拟已经较为成熟, 因此可以将水-热-盐三场耦合分析方法应用于水流-盐分共同作用下的联络通道的冻结施工模拟.

3 工程应用

以南通城市轨道交通1 号线永兴大道站—深南路站区间4#联络通道为工程背景, 开发了多物理场数据监测设备.根据联络通道的实际尺寸, 建立联络通道冻结施工二维数值模型进行模拟分析.对比监测数据与模拟数据, 分析盐分与水头对冻结壁平均温度和冻胀变形的影响.

3.1 工程背景

南通城市轨道交通1 号线永兴大道站—深南路站区间起于永兴大道与长泰路交口的永兴大道站, 呈直线形和曲线形下穿长泰路和永和路, 进入深南路站, 此区间共包含4 处联络通道.如图3 所示, 4#联络通道及泵房位于永和路下方, 与永兴佳园60 幢距离最近处约31 m, 其中心里程为左线SK13+610.373, 隧道中心标高-18.572 m; 右线XK13+631.906, 隧道中心标高-18.584 m.联络通道线间距14.210 m, 联络通道埋深21.70 m, 联络通道所在土层为饱和粉砂层.联络通道采用人工冻结法施工, 冻结壁厚度的设计要求为不小于2.2 m, 平均温度低于-12◦C.

3.2 多物理场数据监测设备

传统人工冻结施工中仅布置温度监测孔, 且传感器位于冻结管内, 并未接触土层, 无法实现同一位置多物理场数据的监测.因此, 开发了一体化多物理场数据监测设备如图4(a) 所示,监测管一端置于冻结壁内部, 另一端连接监测通讯设备.监测设备是一种防水集成监测管装置, 包括端部镂空钢管、普通钢管、隔水部件和传感器.隔水部件的两端分别通过套筒螺纹连接端部钢管和普通钢管, 传感器设置于端部钢管内, 用于采集土层多物理场数据.3 种传感器分别为BSIL-T2 型温度计、TDKYJ30 型孔压力传感器、TR-HTS03 三探针温度-湿度-盐分一体化传感器.3 种传感器用于监测冻结土体中的孔隙水压力、温度、盐分和含水量等数据.传感器测得的数据通过DataTaker DT800 数据采集器进行记录和传输(见图4(b)), 为冻结法施工提供多物理场监测数据.

图4 多物理场数据监测设备和数据采集器Fig.4 Multi-physical field data monitoring equipment and data collector

3.3 冻结数值模型

针对南通市轨道交通1 号线永兴大道站—深南路站区间4#联络通道建立数值计算模型.冻结管的布置如图5 所示, 以冻结管的对称轴为中心, 横坐标为与对称中心的距离, 纵坐标为距离地面的深度.M1∼M4为工程监测点, 仅能测得温度;M5为一体化多物理场数据监测点, 能够测得温度、水压力、盐分和含水率等数据.人工冻结管对称布置在联络通道的开挖外轮廓, 通过分析监测点温度数据, 发现两侧温度监测点的数值存在差异, 因此判断存在地下微水流, 方向为右向左流动.然而, 除了地下水流的作用, 盐分和导热系数也会影响冻结时间.根据温度测试数据, 联络通道所处土层的初始温度约为23.7◦C, 冻结管的侧壁是冷冻系统源, 通过盐水循环提供冷区温度, 盐水温度的变化如图6 所示.通过对冻结管两侧温度监测点数值的试算, 设置渗流水头h分别为0.02、0.05 和0.08 m, 导热系数λs分别为1.7、1.9 和2.1 W/(m·K).饱和粉砂层的多物理场力学参数如表1 所示.

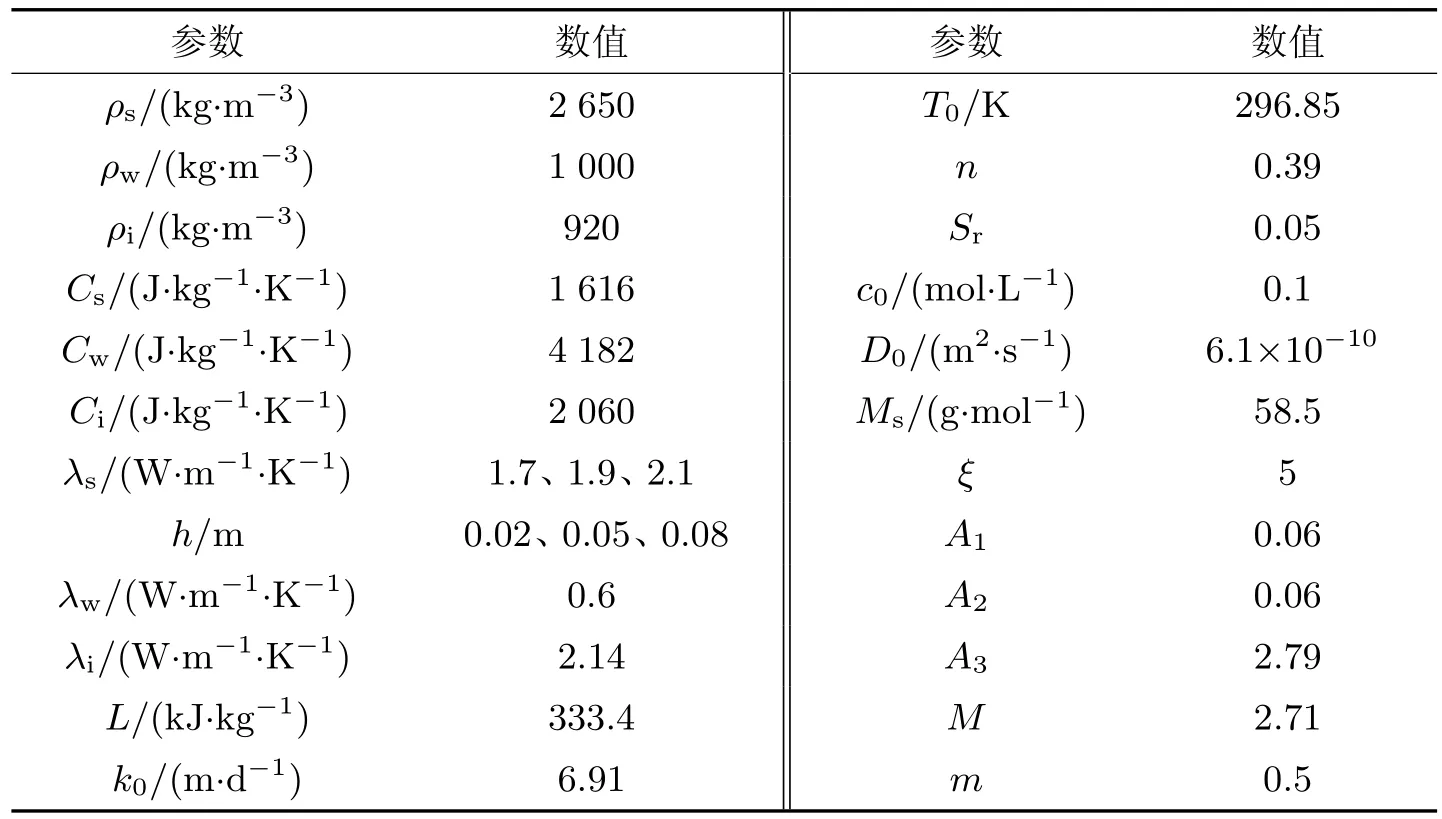
表1 多物理场计算参数Table 1 Multi-physical field calculation parameters

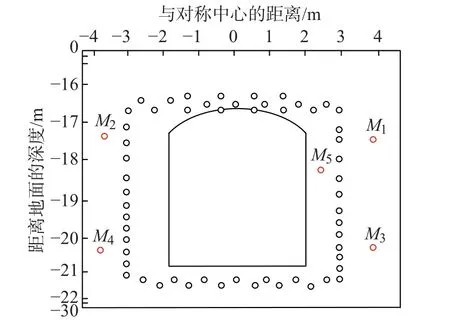
图5 冻结管和监测点布置Fig.5 Layout of freezing pipes and monitoring points

图6 盐水温度变化曲线Fig.6 Temperature change curve of brine

3.4 结果分析

下面通过对模拟结果与监测数据进行对比分析, 讨论水头、盐分和导热系数对冻结过程的影响.基于模拟结果分析冻结壁的平均温度和厚度.

3.4.1 模拟结果与监测数据对比

随着冻结管温度的降低, 土层温度也随之发生变化.在相同环境下, 各点温度的变化趋势一致.图7(a) 分别为不同水头和不同导热系数下,M1点温度的变化.由图可知, 在冻结前期,土层的温度变化较快, 因为冻结管的温度与土层温度相差较大.对比导热系数不变的几条曲线可知, 随着水头的增大, 温度降低越来越慢, 这是因为在地下水流动过程中, 水流带走了一部分能量.当水头保持不变时, 随着导热系数的增大, 温度降低越来越快.当导热系数不变时, 随着水头的增大, 温度降低越来越快(见图7(b)).随着水流从右边流到左边, 左边的监测管获得了更多热量, 并且当冻结壁形成后, 左边受水流的影响会更小, 因此温度下降更快.水头使冻结壁整个向左迁移, 这对冻结时间有较大影响.分别对比图7(a) 和(b) 中模拟数据与监测数据,得出当h=0.05 m,λs=1.9 W/(m·K) 时, 可以获得拟合效果相对较好的计算结果.

图7 不同水头和导热系数下温度的变化曲线Fig.7 Temperature variation curves under different water heads and thermal conductivities

图8 为M3∼M5点监测与模拟数据温度的对比曲线.经过55 d 的冻结,M3和M4点温度变化较M5点相对平缓, 而M3点温度高于M4点, 这是因为水流从右往左流, 带走了一部分热量.模拟结果与监测数据相似度较高, 模型符合实际情况.M5点水压力的变化如图9 所示, 在冻结前期, 水压力基本保持在220 kPa 左右; 大约冻结400 h 时, 水压力发生了跳跃, 达到240 kPa, 从水分场的平衡方程可以得出, 在水变成冰的过程中, 短时间内流进该点的水分不会有很大变化, 渗透系数会急剧减小, 因此水压力突然增大; 随着继续冻结, 水压力慢慢趋于稳定, 最后保持在227 kPa 左右, 这是因为随着不断的冻结, 外部流进该点的水分会不断减少,水流穿过孔隙慢慢趋于稳定, 即水压力也会恢复稳定.

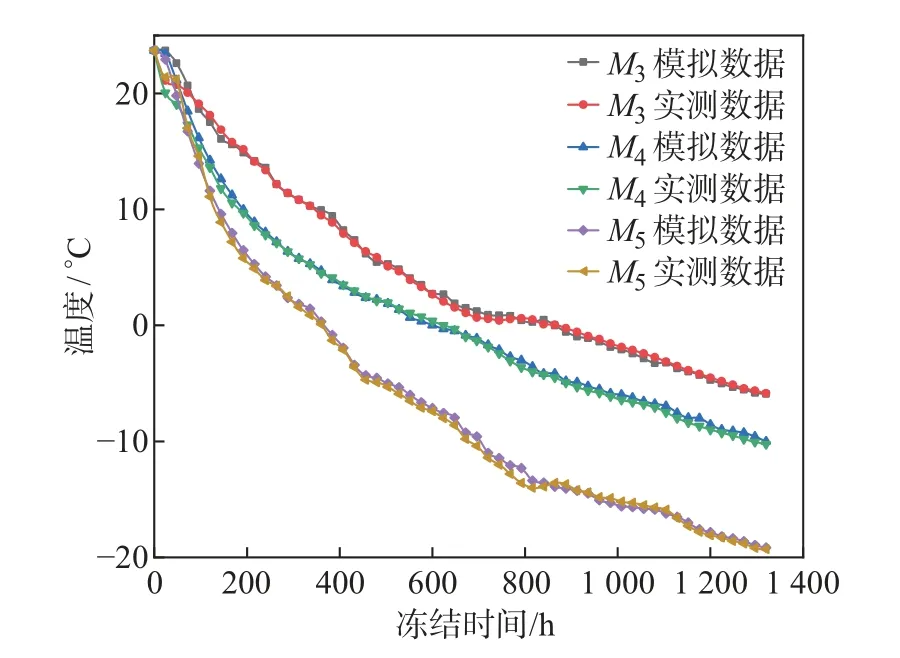
图8 M3、M4 和M5 点监测与模拟数据温度对比Fig.8 Temperature comparison of monitored and simulated data at points M3, M4 and M5

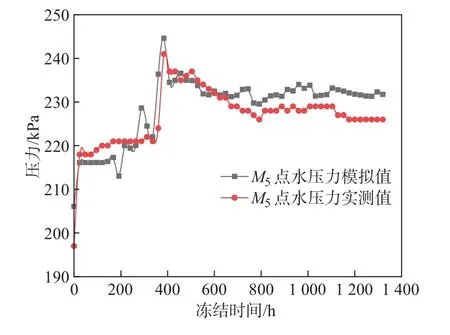
图9 M5 点水压力监测与模拟值对比Fig.9 Comparison between monitored and simulated water pressure at M5 point

M5点盐分浓度的变化如图10 所示.在冻结前期, 浓度几乎不变, 保持在0.1 mol/L; 大约冻结300 h 时, 浓度开始下降, 从0.1 mol/L 降到0.08 mol/L, 这是因为随着该点附近被冻结,水流向冻结处迁移, 导致盐分也随之迁移, 此时盐分浓度会有下降的趋势; 随着继续冻结, 由于盐分数据采集器的原因, 冻结后并未测出监测值, 而模拟值在冻结380 h 左右, 浓度发生较大跳跃, 从0.085 mol/L 增大到0.17 mol/L, 在水-冰发生相变的过程中, 水分慢慢变成冰晶, 未冻水减少, 浓度突然增大, 浓度的增大会反过来抑制未冻水继续被冻结; 随着冻结继续, 浓度慢慢趋于稳定, 最后大致保持在0.15 mol/L, 当水压力趋于稳定时, 未冻水的含量趋于稳定, 浓度也将保持稳定.

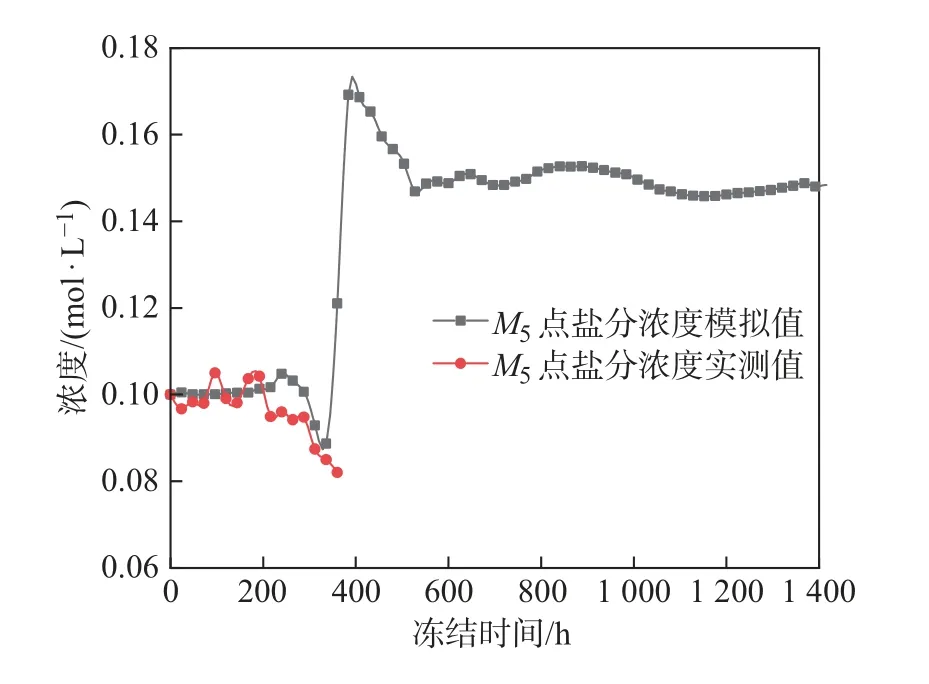
图10 M5 点盐分浓度监测与模拟值对比Fig.10 Comparison between monitored and simulated salty concentrations at M5 point

3.4.2 盐分和水头的影响

图11 为M1点有、无盐分和水头差的温度变化.由图可知, 含盐且有水头的温度变化最慢, 而不含盐且无水头的温度变化最快.当冻结1 320 h 时, 含盐有水头工况下降到-10◦C;不含盐无水头工况达此温度只需1 080 h; 含盐无水头工况达此温度需1 175 h, 比不含盐无水头工况延迟了95 h; 不含盐有水头工况达此温度只需1 255 h, 比不含盐无水头工况延迟了175 h.从上述数据可以得出, 盐分和水头能够延迟该点到达某一温度的时间, 进而影响总体的冻结时间.根据温度场的控制方程, 能够看出水头通过对流的方式带走了一部分能量, 导致温度下降更慢, 而盐分主要影响液体的冻结温度和热物理参数, 导致温度降低更慢.

图11 水头和盐分作用下M1 点的温度变化Fig.11 Temperature change under water head and salt of M1 point

3.4.3 冻结壁厚度和平均温度

判断联络通道是否达到开挖的条件主要依据冻结壁的厚度以及冻结壁的平均温度, 图12为冻结不同时间测线1 和测线2 的温度分布.设计要求冻结壁的厚度为2.2 m, 虚线为设计要求范围, 通过积分法求该范围内的平均温度为冻结壁的平均温度.由图可知, 温度的分布形式为“W” 形, 右侧温度整体略高于左侧温度.

图12 不同冻结时间温度分布Fig.12 Temperature distribution with different freezing time

图13 为上侧、下侧、左侧和右侧冻结壁平均温度和厚度随时间的变化.表2 为各侧冻结壁温度达到-12◦C 和厚度达到2.2 m 所需时间.各侧冻结壁平均温度达到-12◦C 所需时间分别为32、42、45 和50 d, 厚度达到2.2 m 所需时间分别为41、44、44 和48 d.因此, 通过数值模拟可得, 满足设计要求的最少冻结时间为50 d.

表2 冻结壁厚度达到2.2 m 和平均温度达到-12 ◦C 所需时间Table 2 Time required for the thickness of the freezing wall reaching to 2.2 m and the average temperature of -12 ◦C d

图13 冻结壁厚度和平均温度随冻结时间的变化Fig.13 Variation of freezing wall thickness and average temperature with freezing time

由图12、图13 和表2 可知, 冻结壁上壁的厚度和平均温度发展最快, 冻结41 d 就达到了设计要求; 冻结壁右壁的厚度和平均温度发展最慢, 冻结50 d 才达到设计要求; 冻结壁的厚度和平均温度与水头密切相关, 靠近水头一侧的冻结壁厚度比另一侧要薄, 平均温度要高; 冻结壁厚度在冻结15∼25 d 时发展速度最快, 此时正处于冻结壁交圈的时间段.

4 结 论

本工作基于多孔介质的热传导、渗流和盐分的迁移理论, 建立了耦合的物理数学模型, 利用有限元软件COMSOL Multiphysics 模拟南通地铁饱和粉砂地层中联络通道冻结法的施工过程, 得出了如下主要结论.

(1) 考虑盐分对土层冻结温度和未冻水饱和度的影响, 建立了含盐土层的水-热-盐三场耦合方程, 使用COMSOL Multiphysics 数值分析软件建立计算模型, 并在不同水头和导热系数条件下对温度进行确定性分析, 对比监测和模拟数据, 验证了本方法能较好反映含盐土体的冻结过程.

(2) 在土体发生水-冰相变的过程中, 水压力会发生突变, 随着继续冻结, 水压力会趋于稳定.因为当水-冰相变时, 冰会快速填充孔隙, 导致水流很难通过孔隙, 造成水压力增大, 冻结完成后, 水流减小, 趋于稳定, 压力随之保持稳定.

(3) 含盐土层比不含盐土层降温速度更慢, 并且随着盐分浓度的不断增加, 对土层温度的影响增大, 达到同样温度需要的时间更长, 这是因为随着盐分浓度越来越高, 冻结温度会不断降低, 导致温度的变化过程后移, 因此在规定的冻结时间内, 浓度越高, 温度越高.盐分浓度还能通过影响冻结温度来影响未冻水的饱和度, 进而影响冻结壁的厚度.水头主要对上游一侧产生影响, 上游一侧的冻结壁厚度小于下游一侧冻结壁, 这是因为当水流动时, 带走了一部分能量, 使得上游一侧更难以冻结, 造成右侧冻结壁厚度更薄.

(4) 测线部分的温度呈“W” 形分布.右侧冻结壁发展最为缓慢, 厚度达到2.2 m 需冻结48 d.冻结壁达到2.2 m 的同时平均温度达到-12◦C 需冻结50 d.