家庭财富积累是否存在邻里效应？——基于分位数回归梯度提升树模型的分析

蔡超 王乐华

（山东工商学院统计学院，山东 烟台 264005）

一、引言

家庭财富积累是一个家庭生活和发展的物质基础，关系着家庭福利水平的高低。改革开放以来，中国居民家庭财富大幅增加[1]，但居民家庭财富差距较大且呈上升趋势[2-3]。党的二十大报告要求“着力促进全体人民共同富裕，坚决防止两极分化”，实现共同富裕的核心是缩小家庭财富差距。要想缩小家庭财富差距，首先需要明晰家庭财富的积累路径。因此，有必要研究家庭财富积累的主要影响因素，寻找促进家庭财富积累持续增长、缩小财富差距的新动力。

已有文献基于微观数据实证研究了家庭投资和人口特征对家庭财富积累的影响。如Heo和Grable等（2017）[4]、宋宝琳（2021）[5]的研究表明风险投资不但能够增加居民家庭财富积累，还能为家庭提供更多的生活保障。尹志超和张号栋（2017）[6]、胡振（2018）[7]的研究表明居民金融素养的提升能够显著促进家庭财富增长。罗楚亮（2012）[8]的研究表明收入增长能够促进居民财富增长。

已有研究发现个体的行为和决策易受群体中其他个体行为决策的影响[9-10]，将这种他人行为或思想对个体行为决策的影响称为邻里效应。众多学者展开对邻里效应的研究，如余丽甜和詹宇波（2018）[11]指出家庭教育支出存在邻里效应，学历水平的1/5可归因于社区邻里效应。岳华和王海燕等（2021）[12]指出家庭风险金融投资存在邻里效应。谢垩和宋颜群（2021）[13]研究了收入的社区邻里效应，指出邻里效应对居民收入的影响程度较大。社区邻里效应对家庭教育、家庭风险投资、个体收入等都有重要影响，而家庭教育、家庭风险投资和个体收入等对家庭财富积累至关重要，因此，本文推断家庭财富积累也可能存在邻里效应。

然而，目前少有文献从家庭财富积累是否存在邻里效应这个角度展开研究。中国是典型的关系型社会，人与人之间、家庭与家庭之间的交流比较频繁，使中国居民的家庭投资、支出等行为易受他人行为的影响[14-15]。家庭财富积累的邻里效应可能来源于以下三种机制：一是家庭投资理财观念在与其他家庭交流过程中会受到影响，其投资理财的方式与群体中其他家庭趋同。二是人都具有从众心理，家庭投资理财行为会模仿社区中其他家庭，从而产生从众效应或跟风效应[16]。三是财富积累正逐渐成为划分各个社会群体的重要指标[17]。可见，无论哪种机制，都会使我国居民家庭的财富积累与群体平均财富积累表现出正相关关系。

基于以上分析，本文从家庭财富积累是否存在邻里效应这一视角展开研究。谢垩和宋颜群（2020）[18]指出邻里效应具有非线性特征，因此本文在探究邻里效应对家庭财富积累的影响时，采用分位数回归梯度提升树模型这一非线性回归模型进行分析。分位数回归梯度提升树模型一是能够利用其非线性回归模型优势，挖掘邻里效应对家庭财富积累的非线性影响；二是克服了线性分位数回归模型估计性能差的局限，增强了邻里效应对家庭财富积累的估计能力。

与现有文献相比，本文的边际贡献如下：一是从家庭财富积累是否存在邻里效应这一新角度开展研究，丰富了家庭财富积累的相关研究。二是采用前沿的分位数回归梯度提升树模型，规避了传统线性分位数回归模型的缺陷，更好地探究邻里效应和家庭财富积累之间的非线性关系。

二、模型与方法

（一）线性分位数回归模型

线性分位数回归模型由Koenker和Bassett（1978）[19]提出，其描述了解释变量与响应变量之间在不同分位点下的线性关系。线性分位数回归模型不需要满足最小二乘回归模型设定的假定条件，具有更强的稳健性，是一种流行且有效的统计分析方法。假设有训练集，其中yi为响应变量，为解释变量，在τ（0<τ<1）分位点处，线性分位数回归模型可以由下式求解：

其中，β为系数向量，ρτ（u）=u（τ-I（u<0）），I（·）为示性函数。

（二）分位数回归梯度提升树模型

Zheng（2012）[20]和Yuan（2015）[21]提出的分位数回归梯度提升树模型（QRGBT，QuantileRegressionGradient Boosting Trees）是梯度提升树模型在分位数回归框架下的扩展，是一种准确有效的非线性回归模型。分位数回归梯度提升树模型通过不断迭代，利用损失函数的负梯度来拟合生成多个分位数回归树，最终将所有分位数回归树的结果线性相加得到分位数回归梯度提升树模型。生成分位数回归梯度提升树模型的算法具体步骤如下：

步骤2：对于m=1，2，…，n

（a）计算负梯度

步骤3：重复步骤2，共迭代M次，f[M]（τ|xi）即为分位数回归梯度提升树模型的最终估计值。

为增强分位数回归梯度提升树模型的可解释性，本文采用变量相对重要性测度来进一步挖掘模型背后的经济学内涵。变量相对重要性测度是度量解释变量对响应变量的影响程度。Friedman（2001）[22]指出如果在模型中改变某个变量的值，其他变量不变时模型的拟合能力变化较大，则其相对重要性较大。记，…，xi，j=x，…，xi，p）为第j个变量为正常数据时分位数回归梯度提升树模型的估计值为第j个变量为扰动数据时分位数回归梯度提升树模型的估计值，定义下式为第j个变量的重要性测度：

为减少随机性影响，计算100次式（3）的均值作为第j个变量的重要性测度值。本文通过计算变量相对重要性来测度邻里效应对家庭财富积累的影响程度。

本文还希望基于分位数回归梯度提升树模型的估计挖掘出一些解释性意义，因此进一步引入偏相依关系来度量解释变量在不同水平下对响应变量的影响方向和大小，同时揭示变量之间的非线性关系。第j个变量Xj的偏相依关系测度的方法为：剔除Xj的重复值并按照升序排列，记为，并将其依次代入下式计算Xj在不同取值下的偏相依关系值：

三、数据选取与变量描述

本文数据来自2018年中国家庭追踪调查数据（CFPS），样本覆盖31个省（区、市）。删除主要变量缺失的样本后，最终得到9321个有效家庭样本。

将家庭总资产定义为家庭财富积累，并计算家庭财富积累的邻里效应（以下简称“邻里效应”）。根据中国家庭追踪调查数据中的社区编码，将居住在同一农村或同一城市社区的家庭都归类为同一社区，将邻里效应定义为同社区家庭平均财富规模（不包括相应的家庭）。

除此之外，本文还控制了一系列可能影响家庭财富积累的其他因素，包括家庭收入、家庭人口规模、家庭居住地（城镇=1，农村=0）、家庭所在地区（东部=1，中西部=0）、户主年龄、户主性别（男性=1，女性=0）和户主受教育程度（文盲=0、小学=6、初中=9、高中、中专及技校=12、大学专科=15，大学本科=16、研究生及以上=19）。表1报告了变量含义及描述统计结果。从表1可知，家庭财富积累为尖峰右偏数据，且离散程度较大，这说明我国家庭财富积累存在较大差距。

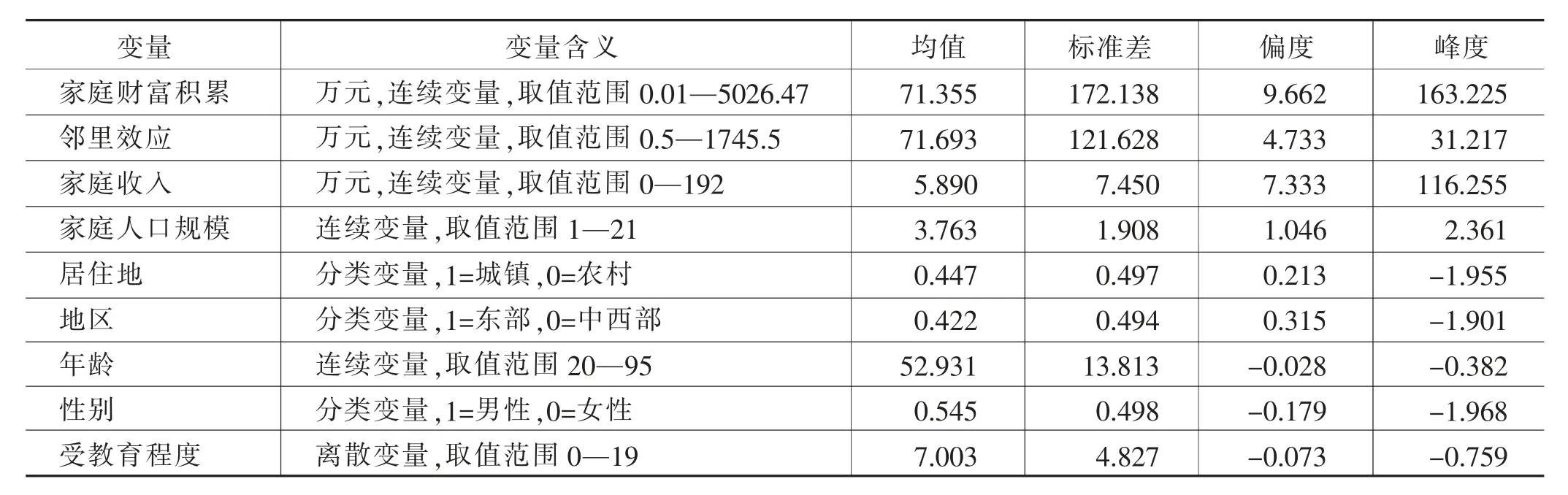
表1 变量含义及描述性统计

四、实证分析

（一）邻里效应能够更好地估计家庭财富积累吗？

本文首先构建了只包含家庭财富积累和家庭、个人特征但不含邻里效应的基准模型（以下简称“基准模型”）。其次，在基准模型的基础上，加入了邻里效应，构建邻里效应模型（以下简称“邻里效应模型”）。两个模型的构建如表2所示。

表2 模型构建

基于上述模型，首先，使用线性分位数回归模型（LQR）和分位数回归梯度提升树模型（QRGBT）分别对两个模型进行拟合。其次，由拟合结果计算分位数平均绝对误差（QAAE）和拟合优度R1，一是评估分位数回归梯度提升树模型是否比线性分位数回归模型更能提升估计性能，二是评估邻里效应模型是否比基准模型更能提升估计性能。

表3报告了线性分位数回归模型和分位数回归梯度提升树模型分别对基准模型和邻里效应模型进行拟合的结果。由表3可知，第一，无论是基准模型还是邻里效应模型，在五个分位点处，分位数回归梯度提升树模型的QAAE值都小于线性分位数回归模型，且分位数回归梯度提升树模型的R1值都大于线性分位数回归模型，说明分位数回归梯度提升树模型更能提升估计性能。第二，在五个分位点处，邻里效应模型的拟合优度都大于基准模型，且邻里效应模型的估计误差也都小于基准模型。说明邻里效应模型对家庭财富积累的估计能力远远大于基准模型，其原因可能为同一社区居民的金融素养、教育偏好、信息获取渠道等因素存在相似性，使同一社区居民的投资行为、财富积累模式等也存在相似性，因此，邻里效应模型对家庭财富积累的估计能力优于基准模型。

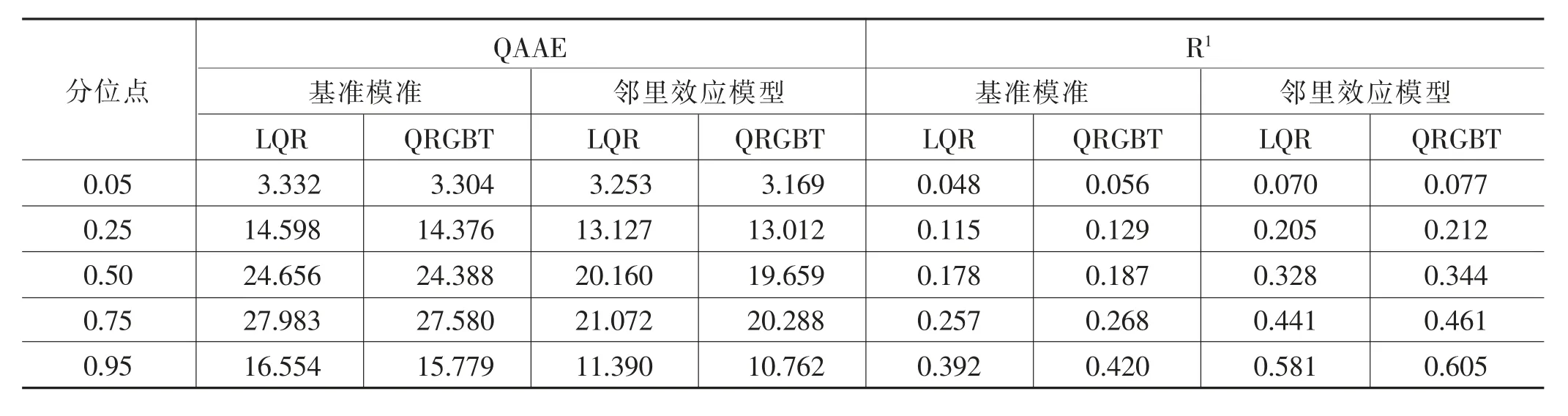
表3 主要拟合结果

（二）变量相对重要性测度

表4报告了解释变量对家庭财富积累影响的重要程度。由表4可知，第一，邻里效应对家庭财富积累的影响程度最大、家庭收入次之，而其他诸如家庭人口规模、居住地、地区、年龄、性别、受教育程度等变量的权重较小。可能原因在于，首先，对于多数普通居民来说，现阶段财富积累的载体仍以住房为主，同一社区的居民所处地段环境与房产价格相似，因此邻里效应对家庭财富积累的影响是最强的。其次，工资收入的储蓄是家庭财富积累的主要途径，因此工资收入对家庭财富的积累是非常关键的因素。第二，从不同分位点上看，在低分位点处，邻里效应的相对重要性程度较高，而在中分位点、高分位点处，邻里效应的相对重要性程度降低，即在家庭财富积累较少时邻里效应的影响更大。其原因可能是财富较少的家庭会面临更大的资源限制和经济机会不足，邻里效应对这些家庭来说可能更为重要，邻居之间的相互支持和资源共享可以提供更多的经济机会和资源，帮助他们改善经济状况。相比而言，财富较多的家庭已经拥有更多的经济资源和机会，对邻里效应的依赖相对较小。

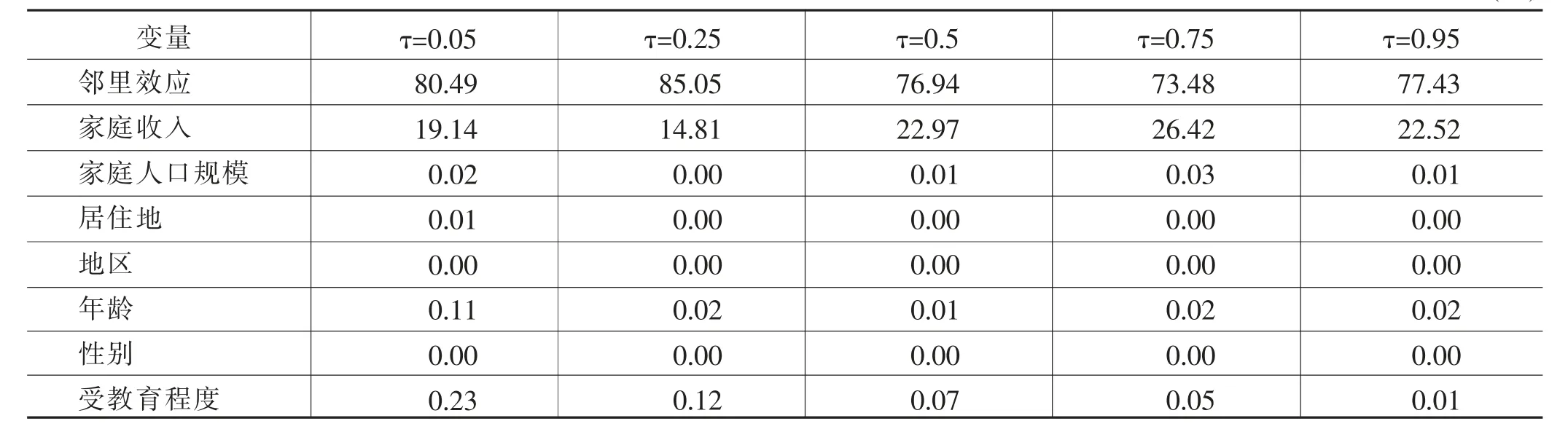
表4 各变量相对重要性权重（%）

（三）邻里效应对家庭财富积累的影响模式

基于变量的重要性分析，继续探究邻里效应和家庭财富积累的具体关联，采用偏相依关系图来考察邻里效应对家庭财富积累的影响。图1展示了在不同分位点处邻里效应对家庭财富积累的影响，其中横轴为邻里效应，纵轴为家庭财富积累。

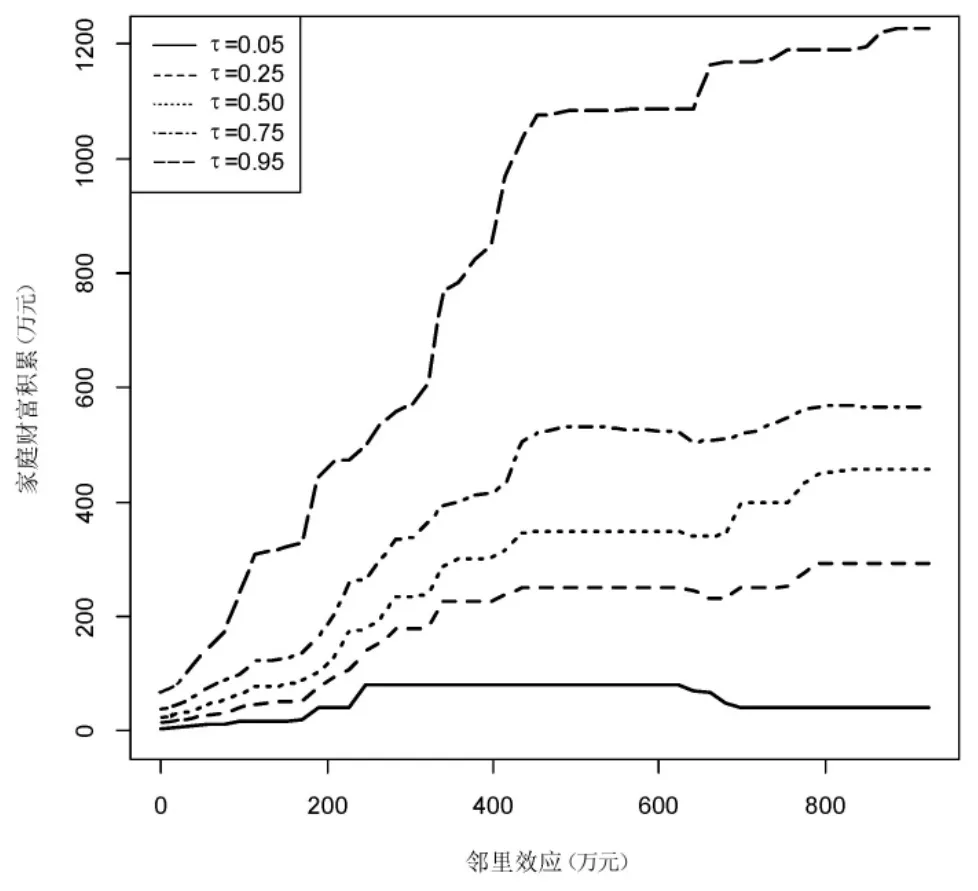
图1 偏相依关系图

从图1可以看出，邻里效应对家庭财富积累的影响具有明显的非线性特征。第一，当邻里效应逐渐增加时，前期（邻里效应为0—450万元）家庭财富积累增长较快，但后期（邻里效应为450万元—900万元）逐渐趋于平稳。这可能是由于财富积累较少时更需要邻里之间的相互支持和资源共享，而随着家庭财富的不断增加，更依赖个人的资源和能力来积累财富。第二，不同分位点处，邻里效应对家庭财富积累的影响不同。在中高分位点处，邻里效应对家庭财富积累的影响较强；在低分位点处，邻里效应对家庭财富积累的影响较弱。其原因可能是财富积累较高的家庭往往具有较强的社交关系和社会资本网络，邻里之间的互动和信息共享可能更有利于家庭财富的积累；相反，财富较少的家庭往往存在较弱的社会资本网络和社交关系，这可能限制了邻里效应对财富积累的影响。

五、稳健性检验

（一）数据缩尾处理

将数据按照家庭财富积累的升序进行排列，删除家庭财富积累值前5%和后5%的数据，对数据进行缩尾处理后再进行估计。表5报告了数据缩尾处理后估计误差和拟合优度的结果。由表5可知，对数据缩尾处理后，分位数回归梯度提升树模型仍优于线性分位数回归模型，邻里效应模型仍优于基准模型，通过了稳健性检验。

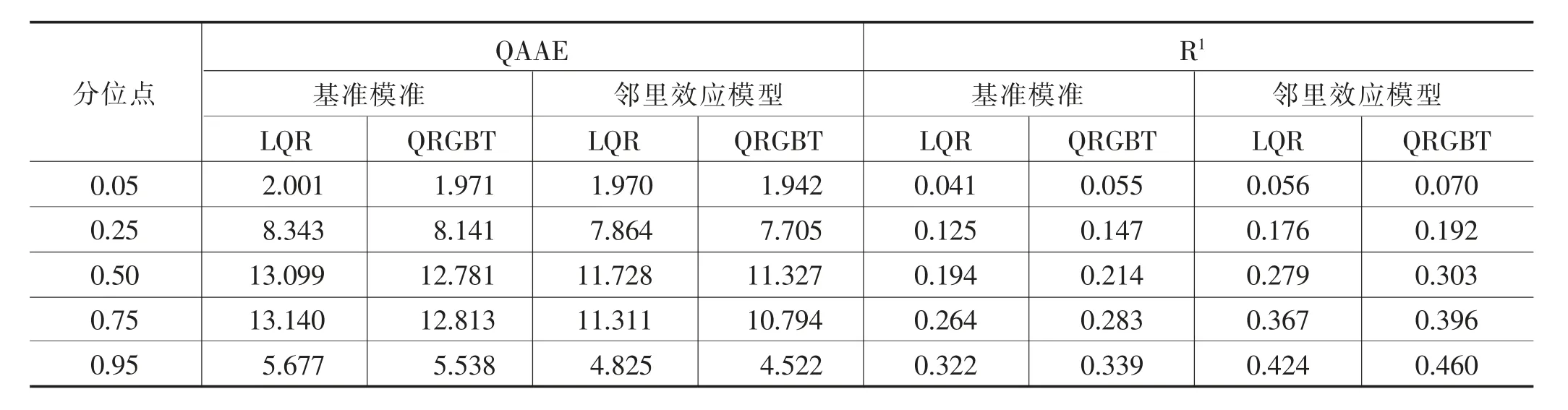
表5 数据缩尾处理后主要拟合结果

（二）更换机器学习方法

分位数回归森林（QRF，Quantile Regression Forest）同样是基于树的集成方法，采用这一方法进行稳健性检验。表6报告了更换机器学习方法后的估计误差和拟合优度结果。由表6可知，相较于线性分位数回归模型，分位数回归森林模型的估计能力有所提高，这与QRGBT的表现基本一致，表明模型是稳定的。

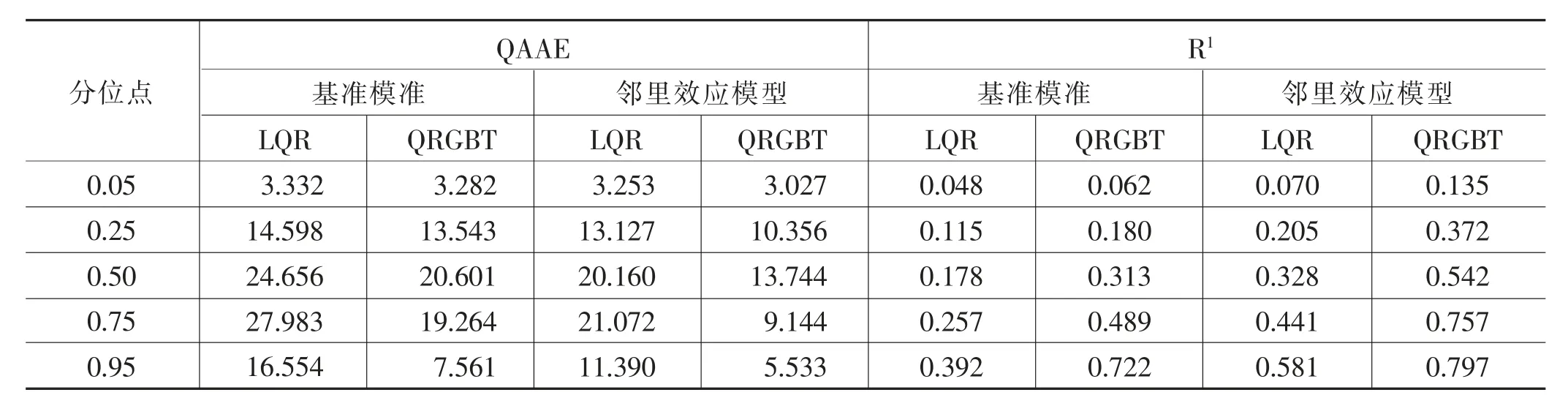
表6 更换机器学习方法后主要拟合效果

六、结论与启示

本文基于2018年中国家庭追踪调查数据，采用分位数回归梯度提升树模型研究邻里效应对家庭财富积累的非线性影响，讨论了邻里效应能否较大程度地估计家庭财富积累，分析了邻里效应对家庭财富积累的影响程度及影响模式。研究发现：第一，在不同分位点处，邻里效应都能更好地估计家庭财富积累；第二，在众多解释变量中，邻里效应对家庭财富积累的影响最强，且邻里效应在财富积累较少的家庭里影响更大；第三，邻里效应和家庭财富积累之间的关系呈现出非线性特点，且在财富积累较多的家庭里非线性特征更为明显。本文不仅从邻里效应这个全新视角对中国家庭财富积累的影响因素进行研究，丰富了家庭财富积累这一领域的文献，而且采用前沿的分位数回归梯度提升树方法规避了传统线性模型的缺陷，更加适用于分析变量之间的非线性和交互关系。◆