不同倾角层状岩体巷道围岩变形破坏特征及机制研究
2024-01-08叶义成
沙 杰 叶义成,2 姚 囝
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室 湖北 武汉 430081)
随着我国巷道施工建设的不断发展,层状岩体围岩在巷道工程建设中经常遇到[1-3],由于层状岩体含有层理结构面,导致其力学特性表现为明显的各向异性[4],其变形破坏特征及机理要比均质岩体更加复杂[5]。为确保层状岩体地下巷道围岩的安全与稳定,有必要针对不同倾角下层状岩体巷道围岩的破坏特征及机理开展研究,这对实际工程具有十分重要的意义。
许多学者采用数值模拟、现场监测和相似模拟的方法对上述问题开展了大量的研究。徐同启等[6]以重庆黔江蒲草沟隧道为依托,利用FLAC3D数值模拟软件分析了不同倾角下隧道拱顶的沉降特征;沙鹏等[7]分析了在高应力条件下,不同层理面角度隧道围岩变形特征及支护受力特征,并提出针对性的支护方案;贾蓬等[8]利用RFPA软件研究了层状顶板巷道围岩的变形破坏特征及不同条件下顶板的破坏规律;彭岩岩等[9]以徐州旗山-1 000 m联络大巷为背景进行了相似模型试验,研究了缓倾斜层状岩体巷道的变形破坏特征;夏彬伟和李丹等[10-11]均以共和隧道为对象,开展缓倾斜层状岩体隧道相似模拟试验,得到不同荷载作用下围岩应力变化规律及破坏特征;吴梦军等[12]通过数值模拟软件MIDAS/GTS对陡倾层状岩体隧道的变形破坏特征及机理进行了探讨,随着层面倾角的增大,发生顺层滑移破坏的概率增大;郭小龙等[13]以杨家坪隧道为依托,采用FLAC3D软件分析了围岩破坏特点,提出高应力陡倾层状岩体软岩巷道的变形破坏机理。
以上对于层状岩体巷道围岩的研究,一方面是针对某一具体倾角开展研究,另一方面是研究者采用基于连续介质理论的有限元方法开展研究,该方法不能克服模型和岩体介质客观属性之间存在的差异,不能准确反映巷道开挖过程中岩体的力学响应行为。因此,本文采用数值模拟的方法,使用离散元模拟软件UDEC对不同倾角层状岩体巷道围岩变形破坏特征并对其破坏机制展开了讨论,以期对层状岩体巷道围岩破坏以及后续采取针对性的支护措施具有理论及实践意义。
1 数值计算模型及参数选取
1.1 计算模型的建立及边界条件
采用非连续介质的通用离散元程序(UDEC)软件,岩层采用基于M-C强度准则的弹塑性本构模型,层理面接触采用Coulomb滑移准则。为了简化层状岩体巷道模型,假设巷道的开挖是瞬时完成的。
根据弹性力学中的圣维南原理,为减小边界效应对巷道开挖的影响,取模型大小为50 m×50 m,巷道断面为直墙半圆拱形,跨度5 m,高度5 m。计算采用裸洞的形式,不考虑支护作用。且为了监测巷道开挖后层状岩体围岩的变形位移大小,在巷道周边设置几个监测点。层状岩体巷道围岩开挖数值模型如图1所示,图中θ为层面倾角。

图1 计算模型(以30°为例)Fig.1 Computational model (Take 30 degrees for example)
巷道开挖之前,对岩体和节理面进行参数赋值,并对模型边界施加应力或位移约束。对模型底部进行竖向位移约束,模型两侧边界固定水平方向位移,顶部边界可根据计算情况对其施加相应的压力以模拟上覆岩体的自重应力σ1,模型两侧施加应力σ3模拟水平应力。为了实现巷道实际情况下的地应力环境,在竖向应力场方向赋予竖向应力变化梯度。
1.2 岩体及结构面参数
根据某层状砂岩为主的巷道施工工程现场,对砂岩的相关力学参数进行取值,岩体与层理面参数见表1。

表1 岩体及层理面计算参数取值Table 1 Parameter value of rock mass and bedding plane calculation
由于在数值模拟计算中需要确定岩体的体积模量和剪切模量,通过以下公式计算:
根据表1中砂岩的弹性模量E和泊松比μ,可以计算得出砂岩的体积模量K为4.4×109Pa,剪切模量G为3.3×109Pa。
1.3 计算工况
巷道埋深取500 m,经计算自重应力为12 MPa,侧压系数取0.8,水平应力为9.6 MPa。层理面垂直距离0.6 m,层理面倾角分别取0°、30°、45°、60°、90°进行计算。为了对比分析层状岩体巷道围岩破坏特征的不同,方案中添加了均质岩体巷道(无层理面),具体方案见表2。

表2 不同倾角层状岩体分析方案Table 2 Analysis scheme of layered rock mass with different dip angles
2 数值模拟结果分析
2.1 不同层理倾角下围岩位移分析
均质岩体和不同倾角层状岩体在巷道开挖后围岩的变形位移特征如图2所示。由图2(a)可知,均质岩体巷道围岩的变形位移仅出现在巷道周边较小区域内,且变形位移值较小,尤其巷道底角处的变形位移相比其余部位更小,其余部位变形位移大小基本相同。相比均质岩体巷道围岩的变形位移,层状岩体巷道围岩的变形位移部位及大小都有着很大的区别。当层理面倾角为0°时,由图2(b)可知,巷道围岩变形位移主要集中在巷道的顶底板处,最大位移值出现在巷道顶板为37.76 mm,其次是底板的30.77 mm,而巷道两帮及底角变形位移相对而言较小,变形位移大小分布左右对称。层理面倾角为30°时,由图2(c)可知,巷道围岩顶底板处的变形位移仍然较大,顶板位移仍达到了30.49 mm,底板30.30 mm,但最大变形位移部位在左侧拱肩处,其大小为38.12mm,右底角的变形位移要明显大于左底角,变形位移大小明显不对称分布,且巷道两帮变形位移大小相比0°倾角时略有增大。层理面倾角为45°时,由图2(d)可知,最大变形位移部位继续向拱肩偏移,大小为37.79 mm,此时巷道顶底板变形位移仍较大,右底角的变形位移远大于左底角的变形位移,变形位移大小不对称分布。层理面倾角为60°时,由图2(e)可知,巷道围岩最大变形位置继续向左侧偏移到拱肩与左帮之间,其大小为37.08 mm,巷道两帮变形位移大小增加明显,左帮的变形位移达到了28.66 mm,右帮变形位移较为明显,大小为31.62 mm,但值得注意的是巷道顶板的变形位移情况有所好转。层理面倾角为90°时,由图2(f)可知,巷道顶底板的变形位移较小,但此时巷道左右两帮的变形位移达到最大,分别为33.35 mm和33.25 mm,变形位移大小左右对称分布。

图2 不同倾角层状岩体巷道围岩径向位移Fig.2 Radial displacement of roadway surrounding rock of stratified rock mass with different dip angles
总体来看:除均质岩体,层理面倾角为0°与90°的层状岩体巷道围岩外,其余倾角的层状岩体巷道围岩的变形位移均呈现明显的不对称性。当层理面倾角从0°~90°的过程中,层状岩体巷道围岩变形破坏的非对称性先增大后减小。值得注意的是,层状岩体巷道围岩变形位移最大的位置始终垂直于层理面方向,由刚开始的顶底板最终变成巷道两帮。
由图2可知,监测点1(顶板)和监测点5(底板)的变形位移随着层理面倾角的增大而逐渐减小,层理面倾角越小,对两处影响越大;监测点8的变形位移大小先有小幅度的上涨,但当层面倾角大于45°时,开始下降,且下降幅度较大,监测点2(右拱肩)的变形位移大小随着倾角的逐渐增大而减小,与监测点8(左拱肩)的变形位移大小变化有所不同。层理面倾角在0°~60°时,监测点3(右边墙)与监测点7(左边墙)的变形位移大小均随层理面倾角的增大而增大,当倾角达到60°时,变形位移大小急剧增大,原因可能是岩层间作用力超过了其极限抗剪强度而引起较大程度的变形位移,层理面角度为90°时,巷道边墙是劈裂挤出破坏,与剪切滑移变形相比程度较轻,且右边墙(顺倾侧)的变形位移始终大于左边墙(反倾侧)。监测点4(右底角)和监测点6(左底角)的位移变化完全相反,右底角位移随倾角的变化先增大后减小,左底角位移随倾角的变化先减小后增大,值得注意的是,层理面倾斜时,右底角的位移始终要比左底角的位移大得多,层理面倾角为45°时,左右底角的位移量相差最大为13.13 mm。
由图2、图3可以看出,当层状岩体层面倾角逐渐增大时,围岩的变形破坏呈明显的非对称性,因此采用非对称的支护方式才能最好地支护倾斜岩层巷道围岩,即应加强控制垂直层理面方向上的围岩。当层面倾角较大时,要注意巷道两帮产生较大的变形破坏,加强两帮的支护强度,当层面倾角较小或近水平时,应加强对顶底板的支护强度。

图3 巷道不同监测点位移Fig.3 Displacement of different monitoring points in roadway
2.2 巷道围岩最小主应力分布
不同层理面倾角下巷道围岩的最小主应力云图如图4所示。
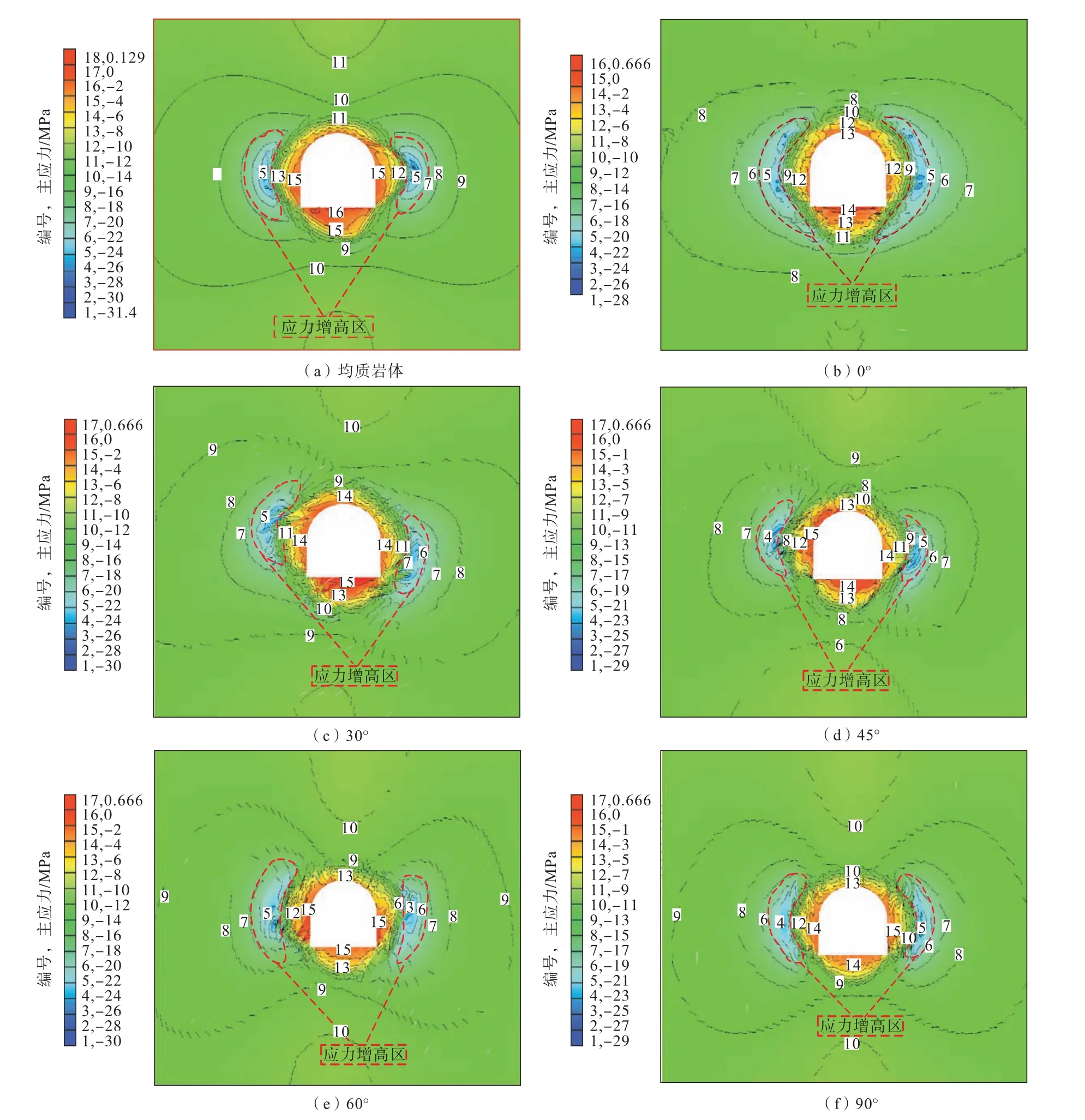
图4 不同层理面倾角最小主应力云图(图中数字为对应图例编号)Fig.4 Nephogram of minimum principal stress at different angles of bedding planes
由应力云图可知,均质岩体、0°、90°巷道围岩的最小主应力云图呈对称性分布。从等值线最小主应力云图可以明显看出,贴近巷道临空面的浅层围岩处于受拉状态,深部围岩都处于受压状态,且应力大小随着距离临空面越来越远表现为先增大后减小。由于层理面的存在,推迟了围岩最小主应力峰值位置的出现,围岩应力得到了释放。均质岩体压应力增高区集中在距巷道两帮一定距离的区域内,且面积较小;0°倾角巷道围岩的压应力增高区除顶底板外,均匀分布在巷道周围,呈“()”型,跨度较大;倾斜层理面巷道围岩压应力增高区逐渐向拱肩位置转移,呈“弯月形”,并随着倾角的增大逆时针旋转,表现为“左轻右重”的分布特点;90°倾角岩体的压应力增高区同样集中在距两边墙一定距离的区域内,但其有明显向围岩深部延伸的趋势,面积较大。
3 破坏机理分析
通过上述层状岩体围岩内部最小主应力分布规律研究结果,对其破坏机理进行分析。
3.1 水平层状岩体巷道破坏机理
水平层状岩体巷道顶板的破坏与材料力学中板梁结构的破坏类似[14]。受到上覆围岩重力及水平应力的作用产生离层现象,即结构面的剪切、张拉变形导致岩层的不同步下沉[15]。层状顶板围岩抗拉剪破坏的能力较弱,成为单层岩梁承载结构后,当单层岩梁承载结构强度达到岩梁的极限时,顶板岩体中间位置开始出现裂隙,由于强度的降低,裂隙不断向上延伸,“梁”最终受张裂拉坏、弯折变形并向巷道内部塌落,如图5所示。

图5 水平层状岩体巷道破坏机理Fig.5 Failure mechanism of horizontal stratified rock mass roadway
水平层状岩体巷道底板的破坏机理与顶板类似,巷道开挖后,应力集中在两帮区域及边墙角,在水平应力和向上的垂直应力的共同作用下底板岩层首先发生剪切滑移、离层破坏,当超过岩体的极限强度时,便会发生挤向巷道内部的底鼓破坏。而一般来说,水平层状岩体巷道的边墙在非高地应力地区较为稳定。
3.2 倾斜层状岩体巷道破坏机理
随着倾角的增大,沿层理面的层间摩擦力增大,层间位移量减小,不利于压力的释放[9],靠近巷道临空面一侧的岩体在垂直层面方向上的力和沿层理面方向上的挤压应力的共同作用下,层理面会先发生张拉破坏(离层),随着破坏的发展,然后发生垂直于层理面方向上的弯折破坏和拉应力破坏。同样地,巷道底板在沿层理面方向的力和垂直层理面方向的力的共同作用下,层理面离层,后随着开挖时间的增加,受层状岩体各向异性力学性质的影响,切向应力增加较快,垂直于层理面方向的裂纹不断向深部发展,并最终发生非对称性的折断性底鼓破坏,如图6所示。

图6 倾斜层状岩体巷道破坏机理Fig.6 Failure mechanism diagram of inclinedstratified rock mass roadway
层理面倾角越大,巷道边墙的稳定性越差。倾角不断增大,围岩沿层理面方向上的下滑分力也越大,当层理面提供的较弱粘结强度不能支持岩体沿层理面方向的下滑力时,这也是造成边墙发生沿层理面方向的剪切滑移破坏的主要原因[16]。巷道开挖后,无有效支护的情况下,层理面的法向应力释放程度较大,相邻层面之间的摩擦阻力大幅减小,在上述2个影响因素的共同影响下,巷道边墙的稳定性较弱。
3.3 竖直层状岩体巷道破坏机理
层理面倾角为90°可以视为倾斜层状岩体的一种特殊情况。巷道开挖后,边墙处的围岩处于二维受力状态,巷道边墙围岩产生很大且与层理面方向平行的切向应力,从而导致产生垂直层理面方向的拉应力,靠近巷道临空面的层理面会先发生层理面剪切破坏,然后发生层理面的拉伸破坏。表层的层理面破坏后,层状围岩在垂直应力挤压和水平应力拉伸的共同作用下,造成边墙围岩的劈裂拉伸破坏,并最终向巷道内部挤出[13],如图7所示。
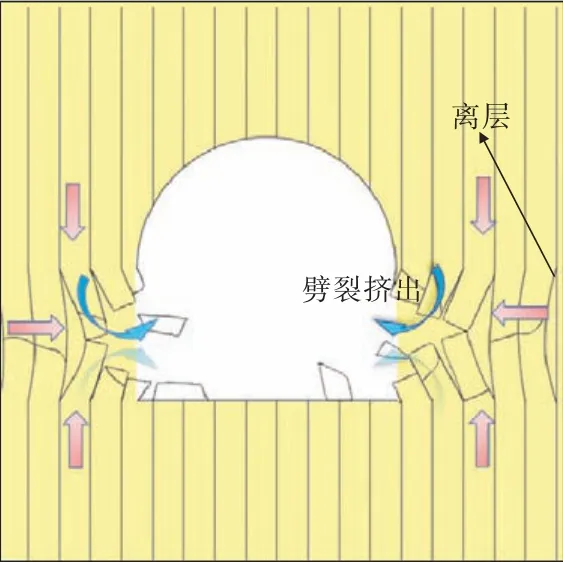
图7 竖直层状岩体巷道破坏机理Fig.7 Failure mechanism of vertical stratified rock mass roadway
4 结 论
(1)受层理面的影响,均质岩体巷道围岩与层状岩体巷道围岩的变形破坏特征存在明显的差异。在给定条件下,当层理面倾角较小时,层状岩体巷道围岩的变形破坏位置最易出现在层理面法向方向。因此,在给定条件下沿易出现破坏的位置加强支护,对增强巷道的稳定性效果更加明显。
(2)在给定条件下,随着层理面倾角的增大,巷道周边的应力分布非对称性增强,造成巷道围岩变形破坏的非对称性。当层理面倾角大于60°时,巷道边墙的变形位移明显增大,但一定程度上减轻了巷道顶底板的不利影响。
(3)巷道开挖后,在地应力的诱导下,在沿层理面方向的应力作用下,首先发生层面剪切滑移变形,然后向临空面方向发生挠曲、离层,最终穿过层理面发生岩体的剪切拉伸破坏。
