基于压缩感知的波形净化及在波形重跟踪中的应用

陆庆虾

(佛山市测绘地理信息研究院,广东 佛山 528000)

0 引 言

基于星载雷达高度计的卫星测高技术由于具备测量精度高,应用范围广,全天时、全天候等优点被广泛应用于对海洋环境和冰川覆盖的监测。内陆湖泊作为海洋和冰川外的重要水资源,对其水位变化进行高精度的监测对局部地区的气候变化,生态环境和经济社会的发展同样具有重要意义[1-3]。因此众多学者将卫星测高技术推广应用于对内陆湖泊的水位监测领域。然而由于内陆湖泊地形复杂且水面宽度较窄,导致目前常用的卫星测高技术的测量精度较低[4,5]。

目前国内外学者对提高卫星测高精度的研究主要包含两个方面:一是参数优化法,通过对电离层延迟,对流层干湿分量和地球物理项等参数进行改正从而提升测高精度[6];二是通过波形重跟踪方法提升卫星测高精度,其原理是针对雷达测高过程中可能存在的误差项进行距离校正,常用的波形重跟踪方法有基于主波峰的波形重跟踪算法,基于阈值的波形重跟踪算法,基于贝塞尔曲线的波形重跟踪算法等[7-9]。传统波形重跟踪算法在应用于海洋和冰川等开阔场景时能够获得较高的测量精度,但是并不适合近海和内陆湖泊等区域的测量。文献[10]提出了多子波参数方法,将最小二乘法应用于测高数据,并利用台湾岛周边水域波形数据验证了该方法的有效性;文献[11]首先对不同测高波形进行分类,进而对每一类波形分别建立最优重跟踪模型提升测量精度;文献[12]在主波峰波形重跟踪算法的基础上,提出一种自适应波形重跟踪算法,有效提升了测量精度。上述方法虽然在一定程度上提升了对内陆湖泊的波形重跟踪精度,但是与开阔水域的测高精度还有一定差距。

内陆湖泊水域所处地形复杂且水面宽度较窄,陆地对雷达信号的反射会导致波形污染从而影响卫星测高雷达的测量精度。针对该问题,本文提出一种基于压缩感知(Compressive Sensing,CS)的波形净化方法,并将其与优化的波形重跟踪算法相结合,从而提升对内陆湖泊的水位测量精度。

1 基于CS的波形净化

当星载雷达高度计信号照射到内陆湖泊时,由于复杂地形等的影响,雷达波形会被污染而产生异常的波峰,从而影响波形重跟踪算法的精度或者造成算法解算失败。因此在进行波形重跟踪之前,需要对波形进行净化。目前常用的波形净化方法将距岸20～30 km处未受污染的波形均值作为参考门限,进而对近岸波形与门限进行比较,当两者之差大于设定的阈值时,认为出现异常值并予以剔除,最后利用异常值周边的数据进行插值修复得到修复后的数据用于后续波形重跟踪算法。该方法在较为开阔的水域(20～30 km)能够获得较好的结果,然而我国还存在大量内陆水体不满足该条件。为此本文提出一种新的波形净化技术,首先提出基于能量均值的自适应异常检测技术,完成异常值的检测,然后利用CS对波形进行建模,并实现异常数据的自动修补,获得净化后的波形用于波形重跟踪。

1.1 异常波峰检测

利用雷达高度计进行水位测量时,事先并不知道异常波峰是否存在以及异常波峰存在时出现的位置,因此异常波峰检测理论上是一个假设检验问题,根据统计理论,最优的假设检验准则是奈曼皮尔逊准则。基于此,本文提出一种结合功率均值的自适应异常波峰检测技术,其具体流程为:

步骤1:从波形最左侧开始,令当前检测单元的序号t=1,当前检测单元为xt;

步骤2:设置保护单元个数为3,参考单元个数为8;

步骤3:根据式(1)计算当前检测xt单元处的门限Tt:

(1)

步骤4:判断当前检测单元xt与门限值Tt的大小,如果xt≥Tt,则认为xt为异常波峰;否则,认为xt为正常波形。

1.2 混合高斯模型

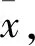
y=Dx+ε

(2)

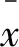
CS是近年来兴起的一种信息压缩技术,其基本原理是只要信号在某个基函数构成的空间内是稀疏的,则可以建立一个与基函数不相关的观测矩阵进行数据压缩,实现高维数据的低维表征,同时可以根据低维表征通过求解一个优化问题实现高维数据的逼真重构。利用CS对式(2)所示问题进行求解首先需要对x的概率密度函数进行假设,然后根据贝叶斯公式推导出已知y条件下x的后验概率密度函数为:

(3)

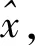
(4)

其中,Ex|y(·)表示求括号内变量的条件期望运算。利用梯度下降法对式(4)进行求解,可以得到最优重构信号的形式为:

(5)

上式表明,式(2)所示波形重构问题的最优解为已知y条件下x的条件期望。

2 波形重跟踪算法

2.1 水位反演原理

星载雷达高度计工作在脉冲模式,向湖/海面发射高能量脉冲信号,脉冲信号经湖/海面反射后回到雷达高度计天线口面,经接收处理获得发射脉冲和接收脉冲之间的延时△t,从而确定卫星与地/海面之间的距离,即高度信息,具体计算方法为:

(6)

其中,R为卫星与湖/海面之间的距离,c=3×108m/s表示光速。

在进行延时测量时,通常采用脉冲前沿的半功率点为基准,然而当内陆湖泊地形比较复杂时,脉冲信号会受到湖面之外的地物反射,导致期望采样点与实际采样点之间出现偏差,从而影响高度的计算。因此需要进行波形重跟踪,从而提升高度测量精度。

2.2 波形重跟踪算法

传统波形重跟踪算法在面对内陆湖泊复杂地形时难以确定脉冲前沿基准点,因此本文采用基于主波峰提取的波形重跟踪算法。主要步骤包括:

步骤1:根据式(7)所示方法提取主峰波形:

(7)

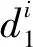
步骤2:采用10%阈值法对步骤1提取的主峰波形进行波形重跟踪;

步骤3:按照式(8)所示IMP准则对步骤2获得的水位值进行评估:

(8)

其中,σraw和σre分别为波形重跟踪前和波形重跟踪后的水位标准差。IMP值越大表明测高精度越高,性能越好。

3 实验及结果分析

3.1 数据来源

采用法国国家空间研究中心的SGDR数据开展实验,该数据是由Jason-2卫星获取,实验数据选取2008年7月—2010年7月的波形数据和卫星高度数据,其中波形数据采样频率为 20 Hz。Jason-2的重访周期为10天,每个完整周期包含254条PASS,其中PASS12为经过长江中游某水文站的轨迹。图1给出了11.55°N～11.95°N区域的采样雷达波形,X轴坐标为采样点序号,Y轴坐标为回波功率,可以看出在采样点序号为300～400范围内,回波功率出现了明显的异常值,如果直接进行波形重跟踪,则异常值的存在会影响测量精度,因此需要首先对异常数据进行波形净化。

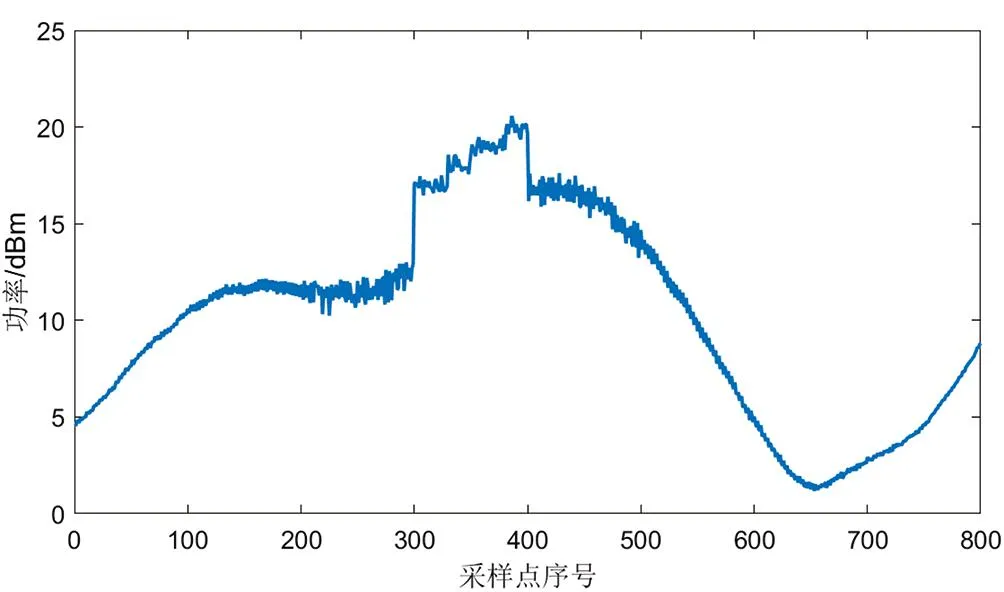
图1 测高雷达接收波形曲线

3.2 实验结果与分析

利用所提功率均值自适应异常波峰检测算法对图1所示雷达波形进行检测得到的结果如图2所示,其中红色曲线为算法得到的自适应检测门限,可以看出,采样点序号为300～400范围内的异常值均位于自适应门限上方,同时由于所提方法是根据波形的功率自动计算获得,因此门限能够随波形功率的变化而自适应变化,在功率较高的采样点处,门限也较高,在功率较低的采样点处,门限也较低,表明所提检测方法具有较强的适应性。

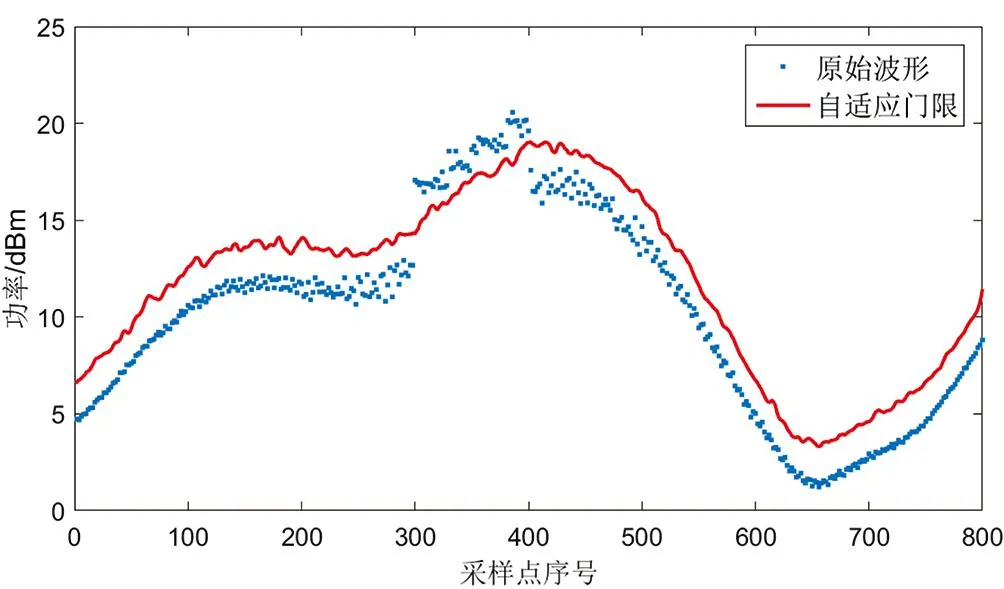
图2 自适应异常波峰检测结果

实现异常波峰检测后,利用所提压缩感知方法进行异常波峰处数据的自动重构得到的结果如图3所示,可以看出,重构后的波形曲线较为平滑,并且很好地反映了原始波形的变化趋势,有利于提升后续波形重跟踪精度。

图3 波形重构结果

为了进一步分析所提波形净化方法对波形重跟踪性能的影响,表1给出了对实验数据的波形重跟踪结果,同时为了对比,表1中一并给出了在相同条件下分别采用传统阈值法,伦敦大学学院法(University College London,UCL)两种方法的波形重跟踪结果。可以看出,所提方法获得的绝对误差最大值为 0.043 m,绝对误差最小值为 0.076 m,误差均方根和相关系数分别为0.723和0.909,四项指标均优于2种对比方法,相对于传统阈值法和UCL法的跟踪精度分别提升28.3%和25.6%,表现出了明显优势,误差均方根更小表明所提方法的跟踪结果更稳定,可靠性更高。

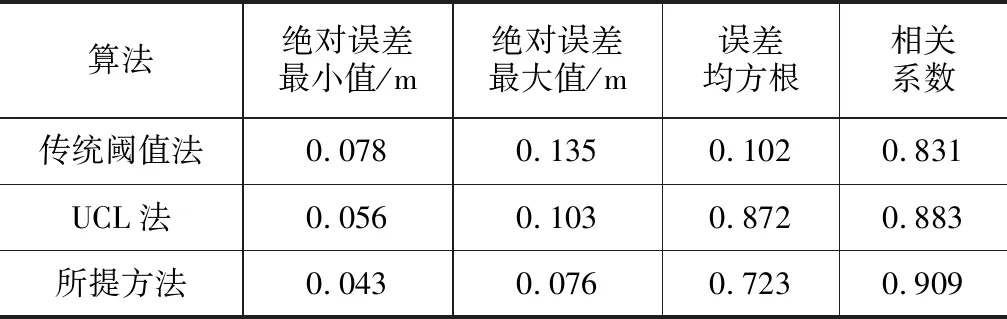
表1 不同方法精度对比

4 结 论

内陆湖泊是我国重要的国土资源,承担着调节河川径流,繁衍水生生物,沟通航运,提供工业与饮用水源,改善区域生态环境等重要任务,因此对其进行水位监测具有重要意义。然而我国有大量的内陆湖泊资源分布在偏远山区,缺少水文观测数据,卫星测高成为唯一选择。由于内陆湖泊地形复杂多变,在水陆交界处会对雷达波形产生“陆地污染”问题,从而影响传统波形重跟踪算法的观测精度。针对该问题,本文提出了一种基于能量均值的自适应异常检测和基于CS的波形重构相结合的波形净化技术,在对异常波峰自动检测的基础上实现了对异常波峰区域波形的高精度重构,基于实际数据的实验表明,所提方法能够有效提升波形重跟踪精度,具有较高的应用前景。