摇摆条件下含花瓣形棒束自然循环系统特性
2024-01-08曹今毅孙建闯孟祥飞张文超杜利鹏蔡伟华
曹今毅, 孙建闯, 孟祥飞, 张文超, 杜利鹏, 蔡伟华
(1.东北电力大学 能源与动力工程学院, 吉林 吉林 132012; 2.东北电力大学 热流科学与核工程实验室, 吉林 吉林 132012; 3.中广核研究院有限公司, 广州 深圳 518031)
相较于传统圆柱型燃料棒,螺旋花瓣型燃料棒的表面积与体积比较大,有效增大了换热面积;螺旋结构强化冷却剂横向交混,显著增强对流换热;燃料组件采用自支撑布置,进一步简化堆芯结构[1]。基于上述优势,花瓣形燃料棒束可采用紧密排列布置技术,在小型反应堆中应用前景广阔。俄罗斯最早开展螺旋花瓣型燃料棒相关研究,并应用在核动力破冰船中[2-3]。Nikolai等[4]在氦冷快堆堆芯中采用螺旋花瓣型燃料组件,以及二氧化钚和贫化铀混合物颗粒的核燃料。Conboy等[5]研究发现,在相同工况下,采用花瓣形燃料的压水堆堆芯,功率比传统圆柱形燃料棒增加47%。Garusov等[6]在额定功率下,考虑流通截面和表面粗糙度影响,得到了花瓣形棒束通道阻力系数和努塞尔数关联式。Zhang等[7-8]研究了单相冷态条件下5×5花瓣形棒束通道横向交混特性,得到了棒束通道内阻力系数关系式。Xiao等[9]采用子通道方法,分析了花瓣形燃料棒束通道内的流场分布,发现中心子通道和边子通道的横向流动方向不同。相关学者也采用计算流体力学(computational fluid dynamics,CFD)方法研究花瓣形燃料棒束内流动换热机理。蔡伟华等[10]基于CFD方法研究了花瓣形燃料棒流动换热特性,结果表明,螺旋节距小于750 mm的棒型,螺旋结构能有效增强燃料棒换热能力。杜利鹏等[11]采用数值研究发现,花瓣形结构会使流速不均,内凹弧产生明显过冷沸腾。Cong等[12]采用数值方法研究了螺旋花瓣型燃料棒束通道内流动沸腾和临界热通量,发现花瓣形燃料临界热通量显著高于圆柱形燃料。
将花瓣形燃料棒应用于海基核动力装置中,需考虑摇摆运行状态对自然循环的影响。谭思超等[13]通过实验发现燃料棒蓄热对壁温波动幅值的影响较大。此外,摇摆附加惯性力会产生附加压降,进而影响系统的自然循环能力[14]。Lai等[15]采用六自由度摇摆台实验研究了不同运动条件下自然循环流动换热特性,提出了适用于湍流区的周期平均摩擦阻力系数的预测关联式。近年来,相关学者提出了一维与三维多尺度耦合模拟方法,不但能获得复杂堆芯三维流场信息,而且系统瞬态响应特性与实验吻合更好。Zhang等[16]采用固定迭代步法的数据交互策略,通过预设固定迭代步数作为数据交互判据,研究了3×3圆柱形棒束通道流动特性。Cai等[17]针对现有固定迭代步法的数据交互策略的不足,提出了基于自适应数据交互的多尺度耦合数值模拟方法,将其应用于自然循环系统,大大提高了计算效率和计算结果的准确性。
含螺旋花瓣型燃料棒束通道自然循环系统流动受摇摆影响特性尚不清楚,极大地限制了花瓣形燃料棒的工程应用。本文采用区域分解方法,建立了多尺度耦合数值模型,分析摇摆运动下含花瓣形棒束通道自然循环流动特性,并修正瞬时阻力系数关系式,为该类型燃料棒的工程应用提供参考。
1 摇摆条件下多尺度耦合模拟方法
自然循环系统回路如图1所示,对除棒束通道外的上升段、下降段、冷凝器等管路和设备建立动态数学模型[18],采用一维程序模拟回路内冷却剂流动情况。

图1 自然循环回路示意Fig.1 Schematic diagram of natural circulation loop
由于花瓣形燃料棒具有独特的螺旋结构,棒束通道内冷却剂会产生明显横向流动。为获得准确三维流场信息,本文采用CFD软件模拟通道内的流动细节,建立摇摆条件下一维程序与STAR-CCM+软件相结合的多尺度耦合数值模型。
本文主要研究横向摇摆对自然循环流动特性的影响。以大地为基准,建立空间直角坐标系O-XYZ,以Y轴为摇摆轴,将摇摆运动看作简谐运动。规定棒束通道上行为负角度,下行为正角度。则摇摆参数变化规律为:
(1)
(2)
(3)
式中:θ为摇摆角度,rad;θmax为最大摇摆角度,rad;ω为角速度,rad/s;β为角加速度,rad/s2;T为周期,s。
1.1 一维数值模型
本文采用控制容积法[19]建立摇摆条件下的动量守恒方程为:
(4)
式中:li为控制体长度,m;Ai为控制体流通截面,m2;G为质量流量,kg/s;ΔPd为驱动压降,Pa;ΔPadd为摇摆附加压降,Pa;ΔPz为总阻力压降,Pa。
驱动压降主要由棒束通道加热段、上升段与下降段流体密度差产生。设下降段流体密度为ρc,上升段流体密度为ρh,则瞬时驱动压降ΔPd为:
ΔPd=(ρc-ρh)gHcosθ
(5)
式中H为换热高差,m。
此外,摇摆运动会引入附加惯性力,摇摆附加压降ΔPadd为[20]:

β×r-2ω×ν]dl
(6)
式中:ω×(ω×r)为法向加速度;β×r为切向加速度;2ω×ν为科氏加速度。
自然循环回路总阻力压降ΔPz,包括管路沿程阻力压降ΔPz,l、局部阻力压降ΔPz,p和棒束通道内阻力压降ΔPz,r。总阻力压降计算公式[17]为:
ΔPz=ΔPz,l+ΔPz,p+ΔPz,r
(7)
式中ΔPz,r为棒束通道内阻力压降,由STAR-CCM+软件计算得到,Pa。
综上,式(4)可改写为常微分方程形式,式中驱动压降、附加压降和总阻力压降可由式(5)~(7)求得,并采用四阶龙格库塔法(RK4)求解[20]。
(8)
式中h为时间间隔,h=hn+1-hn,s。
1.2 螺旋花瓣型棒束通道模型
3×3螺旋花瓣型燃料棒束通道结构和布置方式如图2所示。其中,燃料棒横截面外径为D,内凹弧半径为R1,外凸弧半径为R2,弧连接段长度为hr,棒中心间距为Lp,棒束通道的矩形围板边长为La,燃料棒直径与内凹弧半径之比D/R1=5.1,与外凸弧半径之比D/R2=10.3,围板长度与棒直径之比La/D=3.2,棒间距与棒径之比Lp/D=1.1,棒束通道总长度Z=800 mm。

图2 花瓣形燃料棒束几何模型Fig.2 Geometric model of petal-shaped fuel rod
本文系统工质为水,为准确模拟花瓣形棒束通道流动换热特性,选取系统压力p=0.5 MPa,温度为298~418 K内水的物性参数,拟合后导入CFD软件计算。将一维程序作为入口速度,设出口为压力出口。为计算准确,首先完成稳态竖直条件下的多尺度耦合模拟,待收敛后,将该结果作为初始场,进行摇摆运动下的耦合模拟。目前,国内外学者已采用CFD方法,开展了螺旋花瓣型燃料棒束通道内流动换热特性研究。结果表明,SSTk-ω湍流模型[21]能准确模拟花瓣形燃料棒束通道热工水力行为[10,12,17]。因此,本文采用该湍流模型开展摇摆条件下多尺度耦合模拟研究。
1.3 数据交互方法
本文采用动态链接库实现一维程序与三维软件间的数据交互[20]。交互参数为棒束通道入口温度Tin、出口温度Tout、进出口压降Pij、自然循环流速v和时间tn项。图3给出了数据交互流程图,具体如下:在STAR-CCM+软件中读取稳态参数,并调整加热段摇摆姿态,然后计算进出口压降和出口温度值,完成后进行收敛标准判断,收敛标准为进出口压降的极差[20]。若通过判定,则将相关计算参数传递给一维程序,在一维程序中计算各分段压降后,采用RK4法计算下一时间步的自然循环流速v,计算完成后采用动态链接库传递给CFD软件,用于后续迭代计算。经多次重复上述一维与三维数据交互过程,直至达到预期时间tpre,则完成全部摇摆条件下多尺度耦合模拟。

图3 一维与三维数据交互流程图Fig.3 Flow chart of 1-D and 3-D data interaction
2 多尺度耦合模型验证
本文选用文献[22]中自然循环系统实验装置和数据验证摇摆条件下多尺度耦合模型。该实验系统由摇摆装置、测量系统、自然循环主回路和冷却回路组成。
验证工质为水,建立工质物性与温度的函数表达式,并将其加载到CFD软件中,工况详细参数设置参考文献[16]。图4给出了入口温度75 ℃,热流密度59 kW/m2,最大摇摆角度20°,摇摆周期30 s的实验结果与耦合模拟结果的入口流速与压降对比图。结果表明,模拟值与实验值吻合效果较好。在波峰和波谷处,入口流速最大相对误差为7.19%,压降最大相对误差为1.16%。模拟结果与实验结果的平均流速相对误差为0.16%,平均压降相对误差为0.47%。耦合模拟得到的流速和压降结果均在可接受范围内,这说明本文建立的摇摆条件下一维与三维多尺度耦合模型可用于含花瓣形棒束通道自然循环系统热工水力特性分析。
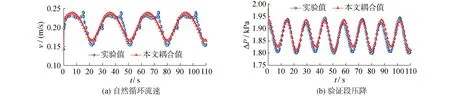
图4 实验结果与耦合模拟结果验证Fig.4 Verification of coupling simulation results and experiment results
3 耦合模拟结果分析
基于摇摆条件下多尺度耦合数值模型,本文开展3×3花瓣形燃料棒束通道自然循环系统流动特性研究,热工参数和摇摆参数如表1所示。

表1 工况参数设置Table 1 Setting of operating parameters
3.1 压降波动特性
3.1.1 压降组成
摇摆运动会导致自然循环系统回路空间位置变化,还会引入附加惯性力,从而显著影响自然循环系统流动特性。为研究自然循环条件下棒束通道内压降波动特性,取棒束中间600 mm作为测压段,将测压段总压降ΔPt,分离为测压段摇摆附加压降ΔPadd,t、流动阻力压降ΔPz,t和重位压降ΔPg。图5给出了加热功率10 kW,入口温度40 ℃,最大摇摆角度10°,摇摆周期20 s条件下各压降和体积流量Qv随无量纲时间(t/T)变化曲线。

图5 压降和流量变化曲线Fig.5 Variation curves of pressure drop and flow rate under rolling motion condition
可以看到,测压段总压降ΔPt与摇摆角度θ的周期相同,同一周期内测压段总压降ΔPt相邻波峰幅值不同,这是各组成压降共同影响的结果。测压段重位压降ΔPg占比最大,因此与总压降ΔPt波动规律相似。在一个周期内,棒束通道2次运动至与地面垂直位置,此刻重位压降达到最大值,而测压段摇摆附加压降ΔPadd,t为零,摇摆运动使竖直姿态下流体密度不同,从而导致测压段重位压降相邻波峰辐值不同[23]。
3.1.2 流量和阻力压降相位特性
图6给出了不同加热功率下自然循环流量G和测压段阻力压降ΔPz,t相位关系曲线。结果表明,流量和阻力压降曲线的相位差并不明显,最大不超过摇摆周期的4.5%,与自然循环系统中圆柱形棒束通道[23]和矩形管道[24]的研究结果相同。此外,波谷位置处的相位差要比波峰位置的更大,这是由于波峰、波谷处的流体温度相差较大,流体物性变化显著,致使驱动力变化不一致,以及棒束通道阻力系数改变而导致的。
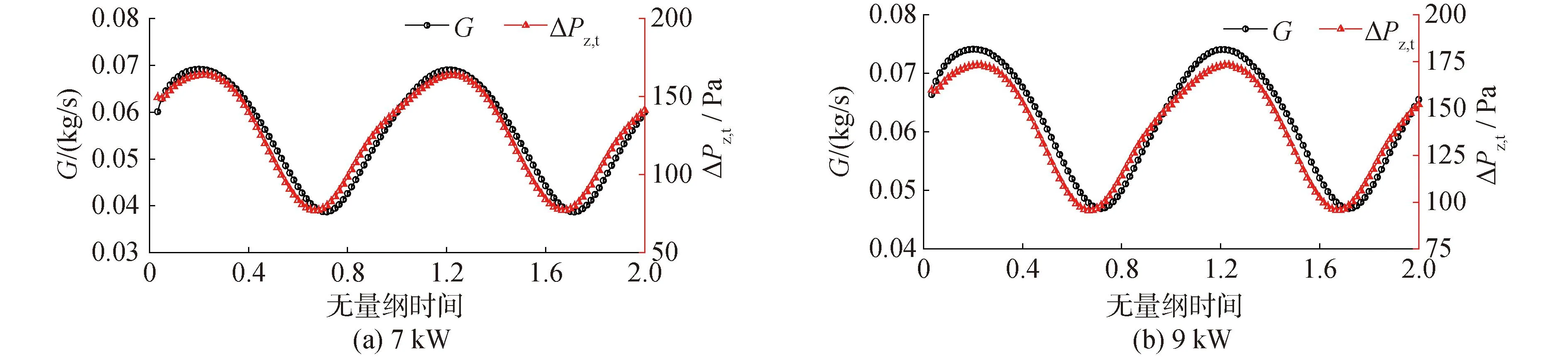
图6 不同加热功率下流量和阻力压降相位变化Fig.6 Phase shift between the flow rate and resistance pressure drop
3.2 加热功率影响特性
3.2.1 加热功率对自然循环流量的影响
自然循环流量是自然循环系统研究的重要参数之一。为便于定量评价曲线波动特性,定义体积流量相对值(QV)re为:
(QV)re=QV/(QV)av
(9)
式中:QV为瞬时体积流量,m3/h;(QV)av为摇摆条件下时均体积流量,m3/h。
图7所示为不同功率下,流量波动曲线。加热功率升高,自然循环流量值增加,波动幅度减小,且功率从5 kW增加到9 kW,波谷区流量的变化量较波峰区提高19.81%。

图7 不同功率下流量波动曲线Fig.7 Fluctuation curves of flow rate at different powers
由式(5)可知,在摇摆条件下,当有效高差不变,驱动压降由密度差决定。提高燃料棒功率,流体吸热量增加,温差增加,密度差增大,驱动压降增大,流量提高,波动幅度减小,系统更稳定。此外,由于阻力压降与流量的平方满足正比关系,高流量下阻力压降变化比低流量的更显著。在相同驱动压降变化时,低流量条件下,驱动压降与阻力压降满足准稳态匹配所需流量的变化量越大[25]。因此,波谷区流量的变化量较波峰区的更大。
3.2.2 加热功率对阻力系数的影响
为进一步分析螺旋花瓣型棒束通道内流动阻力特性,图8给出了不同功率下棒束通道内流动阻力系数随时间变化曲线。其中,阻力系数可通过达西公式求得[26]。结果表明,随燃料棒加热功率升高,棒束通道内阻力系数降低,并趋于平缓。

图8 不同加热功率下阻力系数波动曲线Fig.8 Fluctuation of resistance coefficients of fuel bundle channels for different heating powers
图9给出了τ=0.75时不同燃料棒加热功率下z/Z=0.5处粘度分布。结果表明,功率从5 kW提高到9 kW,流体温度升高,近壁面流体平均粘度从3.32×10-4Pa·s降至2.91×10-4Pa·s,粘度降低。壁面粘滞力减小,阻力系数随之降低。
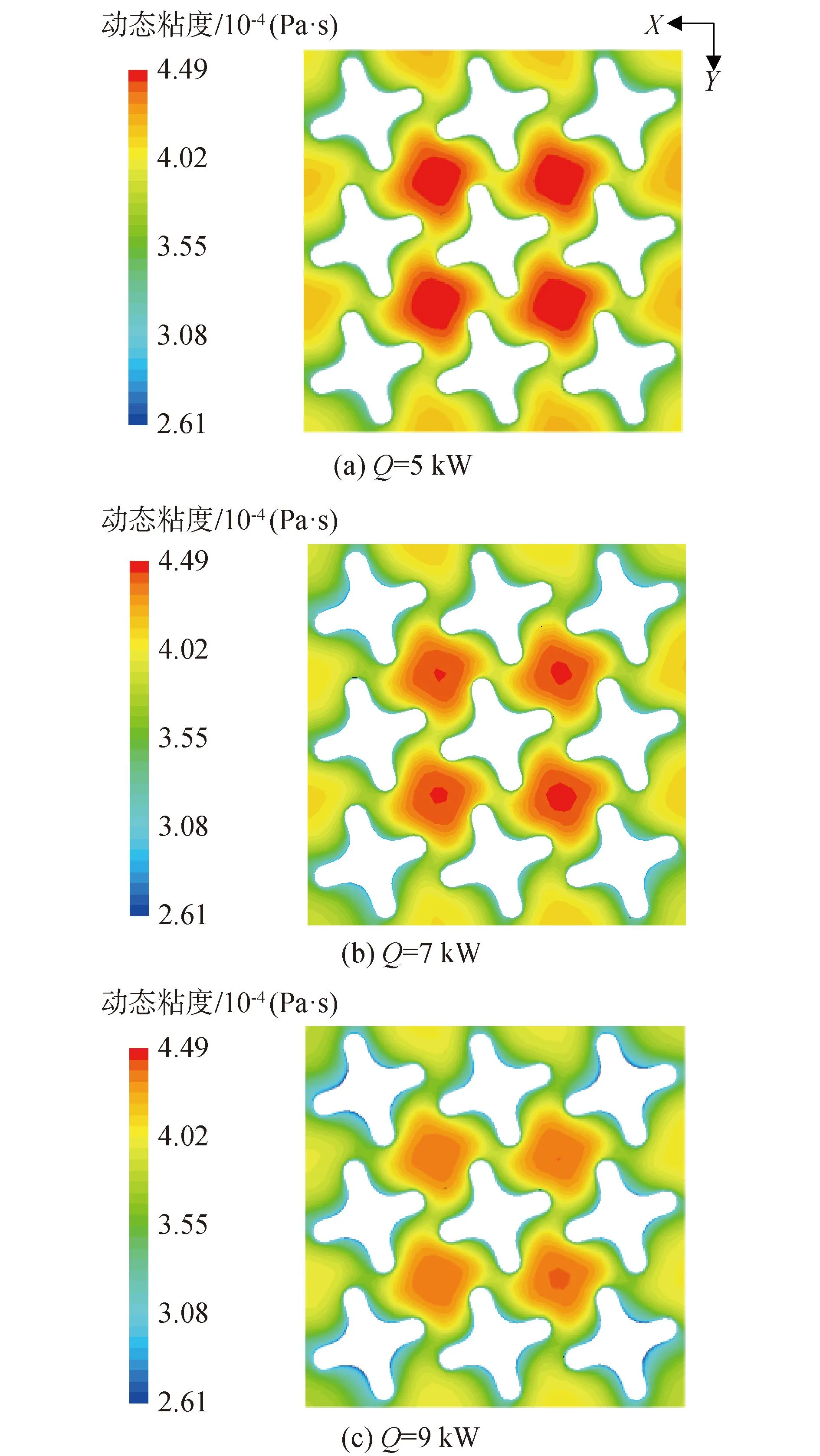
图9 不同加热功率下棒束通道z/Z=0.5处粘度分布Fig.9 Viscosity distribution at z/Z=0.5 of fuel bundle channel for different heating power
3.3 阻力系数关联式
摇摆条件下花瓣形燃料棒束通道内流动阻力特性除考虑流动参数和热工参数的影响外,还需考虑摇摆角度θ和摇摆周期T等摇摆参数影响。因此,描述摇摆条件下棒束通道内阻力特性的函数关系式为:
F(ΔPf,ρ,v,r,L,De,μ,ω,β,Tb,Tw)=0
(10)
式中:r为棒束通道中心到摇摆轴的距离,m;L为测压段长度,m;De为当量直径,m;μ为动力粘度,Pa·s;Tw和Tb分别为棒表面和主流平均温度,K。无量纲化后可以得到Re、L/De、Tw/Tb、ωr/v和βrDe/v2等无量纲数。其中,ωr/v表示切向惯性力与流动惯性力之比,βrDe/v2表示法向惯性力与流动惯性力之比。流动阻力压降为:
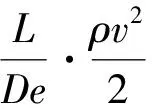
(11)
相较于静止条件,摇摆条件下棒束通道内流动阻力系数λ会受流体自身惯性力、黏性力,以及摇摆附加惯性力影响:
λ=f(Re,ωr/v,βrDe/v2,Tw/Tb)
(12)
摇摆条件下圆柱形棒束通道流动阻力系数经验表达式一般形式[27]为:
(13)
式中:μb为主流动力粘度,Pa·s;μw为燃料棒近壁面流体动力粘度,Pa·s;μw/μb用于考虑Tw/Tb的影响。
此外,流体因摇摆运动而受到摇摆附加惯性力作用。因此,通过引入瞬时摇摆雷诺数[23,27],准确描述自然循环系统的瞬态特性为:
Reroll=ρωrDe/μ
(14)
式中Reroll为摇摆雷诺数。
(15)
考虑到流道进出口效应,选取花瓣形棒束通道中间600 mm长度进行研究,对于摇摆角度15°~25°,摇摆周期20~30 s,瞬时雷诺数800~2 000内的2 000个瞬时数据进行拟合,计算得到式(13)中的系数m=-1.856,以及系数bi的计算表达式为:
(16)
图10给出了瞬时摩擦阻力系数耦合模拟计算值和预测值的对比结果。

图10 瞬时阻力系数耦合值λn与预测值λp对比Fig.10 Comparison of resistance coefficient between coupling simulation results λn and predicted values λp
可以看到,计算的相对误差集中在-5%~7%,本文所得关联式在低雷诺数范围内能较好地预测摇摆条件下瞬时阻力系数。
4 结论
1)自然循环条件下,流动阻力压降与自然循环流量相位差不明显。波峰、波谷处流体温度变化,导致波谷处的相位差大于波峰处的数值。
2)加热功率升高,会使自然循环系统更加稳定。驱动压降与阻力压降须满足准稳态匹配,波谷区流量的下降量较波峰区流量上升量更大。
3)通过引入瞬时摇摆雷诺数,获得适用于摇摆条件下自然循环系统流动阻力系数预测式。结果表明,本文模拟值与预测值相对误差集中在-5%~7%。对不同类型花瓣形棒束通道,仍需分析结构参数对阻力系数的影响。
