热电联产压水堆核电机组解耦控制

2024-01-08张茹孙培伟魏新宇

哈尔滨工程大学学报 2023年12期

张茹, 孙培伟, 魏新宇

(西安交通大学核科学与技术学院, 陕西西安 710049)

核能的综合利用是国家推进能源革命、实现低碳清洁发展的重要组成部分,我国倡导积极安全有序发展核电,开展核能综合利用示范[1],核能供热具有大体量、清洁、稳定可靠、价格有竞争力等特点,其将深刻影响我国未来能源革命的走向。1964年,世界上首个核能供热项目在瑞典沿海地区投入使用,该核电站主要功能为集中供热同时生产少量电能[2]。苏联设计建造了多个热电联产核电站为住宅区以及工业区提供电力和热能[3]。Miller[4]提出从核电站背压汽轮机或从汽轮机抽汽来供热的热电联产系统。我国核能供热发展较早,但目前仍处于起步阶段。中核集团从1959年开始设计并建造49-2泳池式轻水反应堆,2017年发布可实现区域供暖的“燕龙”泳池式低温供热堆(DHR-400)[5]。国家电投集团于2015年开始微压供热堆HAPPY200的研发工作[6]。海阳、秦山和红沿河等核电站核能供暖项目已经投用[5,7-8],田湾核电站核能工业供汽项目也正在建设[9]。电厂供热改造后,一回路系统、二回路系统以及供热系统之间的连接会让系统之间产生一定的耦合,给系统的控制带来挑战。当供热负荷增大后,3个系统间耦合性增加,因此需要对热电联产核电机组进行解耦控制以解决耦合性的影响。

本文针对某压水堆核电站,采用打孔抽汽中主蒸汽集管抽汽的供热方案进行改造,供热负荷给反应堆功率控制系统以及汽轮机调节系统都带来了影响,因此首先通过辨识方法建立系统的传递函数模型,然后采用相对增益矩阵(relative gain array, RGA)方法进行耦合性分析,最后采用单位阵解耦法对耦合性较强的系统进行解耦控制,并在Matlab/Simulink仿真平台上验证。

1 热电联产压水堆核电机组对象模型

本文针对某压水堆核电站,采用主蒸汽集管抽汽的方案进行供热改造,抽汽方案如图1所示。核电站进行供热改造后,核蒸汽供应系统产生的蒸汽一部分进入汽轮机,另一部分进入供热系统,一回路系统、二回路系统以及供热系统通过主蒸汽集管连接,都会对主蒸汽集管压力产生影响。3个系统之间存在了一定的耦合性,为了量化系统之间的耦合关系,分析系统间的耦合性,首先需要获得被控对象模型。

图1 供热改造抽汽方案示意Fig.1 Schematic diagram of steam extraction scheme for heating reform

本文研究的压水堆核电站运行方案为二回路蒸汽压力恒定。因此,在机跟堆模式下,供热改造前一回路系统被控量为核功率,二回路系统被控量为主蒸汽集管压力。为了尽量减少供热改造的工作量,供热改造后,一回路和二回路系统不改变,供热系统被控量为供热系统用户侧蒸汽压力;而堆跟机模式下,供热改造前一回路系统被控量为主蒸汽集管压力,二回路系统被控量为电功率。同样地,供热改造后,一回路和二回路系统不改变,供热系统被控量为供热系统用户侧蒸汽压力。供热改造后各控制系统的输入输出关系如表1所示。

表1 供热改造后模型输入输出关系

在不同供热蒸汽流量下,分别引入ρ、V1和V2的阶跃扰动,通过Matlab传递函数辨识工具箱对仿真平台上的一回路系统、二回路系统以及供热系统模型进行辨识,得到机跟堆和堆跟机模式下系统传递函数模型如图2所示。

图2 系统传递函数模型示意Fig.2 Schematic diagram of system transfer function model

2 耦合性分析

从得到的传递函数可知,控制变量与被控变量相互影响,一个控制变量的改变同时会引起几个被控变量变化,该现象称为耦合。相对增益(relative gain, RG)是度量、分析耦合的一个简单实用的指标,以RG为元素的矩阵构成相对增益矩阵(relative gain array, RGA)[10]。该方法只需要已知被控过程的输入与输出系统之间的稳态增益,就可以判断系统的互联程度并且能辅助控制系统设计。RGA中每行或每列的总和均为1,RG反映了通道之间的稳态增益受其他回路的影响程度。当RG接近1时表明,由该输出和输入进行变量配对构成控制回路时可以获得较好的控制效果,因此希望得到的多变量系统的RGA对角元素均接近1,即为对角占优[11]。在机跟堆模式下,汽轮机负荷与供热负荷形成的二回路总负荷跟随反应堆功率变化,此时反应堆功率跟踪设定值。供热改造后,供热调阀开度变化对主蒸汽集管压力产生影响,主调阀可以较快做出响应,将主蒸汽集管压力控制在其设定值,对核功率影响较小,因此该模式下对解耦的要求不高。加入控制器后多输入多输出系统可以进行多个单输入单输出的控制,本文对机跟堆模式不进行讨论。

堆跟机模式下,供热蒸汽在不同额定流量下,通过辨识得到相关传递函数,计算得到RGA分析系统耦合性。其中,矩阵下标数字表示供热蒸汽不同额定流量的量值,其代表供热蒸汽流量占总蒸汽产量的百分比,得到的结果为:

(1)

(2)

(3)

(4)

(5)

对于多变量系统,当RG接近于1,表明其他通道对该通道影响很小,该通道的输入对输出配对合适,不需要进行解耦措施;当RG小于或接近于0时,说明该输入对输出配对不合适,即该输入对该输出没有影响;当RG在0.3～0.7或大于1.5时,则表明系统存在耦合,即该回路的输入对输出有一定影响[11]。

因此,从式(1)可以看出,当供热蒸汽流量为11.4%时,M11.4%(1,1)、M11.4%(2,1)、M11.4%(1,2)和M11.4%(2,2)均在0.3～0.7,表明系统之间存在耦合,ρ的变化对p和Pe、V1的变化对p和Pe都有一定的影响。而M11.4%(3,3)接近1,说明供热系统不受其他系统回路的影响。M11.4%(1,3)和M11.4%(2,3)均接近于0,说明V2的变化对p和Pe没有影响。M11.4%(3,1)和M11.4%(3,2)接近于0,说明ρ和V1的变化均对ph没有影响。

而通过上述其他RGA中各参数接近1的情况可以看出,当供热蒸汽流量越来越大时,M(3,1)越来越大,相对地,M(3,2)越来越小,且M(1,3)也越来越大。这些结果表明,随着供热蒸汽流量的增大,供热系统对一回路、二回路系统的影响增大,系统之间耦合性变大,需要对系统进行解耦来达到调控制的目的。因此,本文选择额定供热蒸汽流量57.0%时的系统进行解耦控制研究。

3 解耦控制

解耦控制器设计的主要任务是解除系统变量之间的耦合。常见的解耦控制系统设计方法包括前馈补偿解耦法、对角阵解耦法和单位阵解耦法。采用不同的解耦方法均可以达到解耦目的,其中前馈补偿解耦法和对角阵解耦法都是解除交叉通道,并使其等效成多个独立单回路系统。而单位阵解耦法除了能获得好的解耦效果,还能提高控制质量[12]。因此本文选择单位阵解耦法进行解耦控制器设计。

另外,多变量解耦有静态解耦和动态解耦之分。静态解耦只要求过程变量达到稳态时实现变量间的解耦,过程中可将传递函数简化为比例系数。动态解耦则要求无论在过渡过程还是稳态,都能实现变量间解耦。当补偿装置各元素的动态特性相等或相近时,可以用静态解耦的办法来解决相关问题;当补偿装置数学模型复杂时,可以用静态解耦来达到解耦目的。本文采用静态解耦方式进行解耦,可以简化解耦装置,而且容易实施[13]。

系统解耦控制系统如图3所示,设传递函数D(s)为解耦器;耦合系统传递函数为G(s);Gc(s)为控制器。

图3 解耦控制系统结构Fig.3 Structure diagram of decoupling control system

单位阵解耦法要求被控对象的矩阵与解耦环节矩阵的乘积等于单位阵[12]:

(6)

式中:G(s)、D(s)分别为传递函数矩阵和解耦矩阵:

(7)

(8)

设计静态解耦补偿器时,根据终值定理:

(9)

代入式(6):

G(0)D(0)=I

(10)

当G(0)可逆时,有[10]:

D(0)=G-1(0)

(11)

当额定供热蒸汽流量为57.0%时,得到解耦器矩阵:

(12)

分别在60 s时将ρ阶跃+0.1dollar,V1阶跃+0.1,V2阶跃+0.1,对解耦器进行开环测试,p、Pe和ph变化量结果如图4～6所示。从图4可以看出,当ρ阶跃扰动后,p增加幅度减小,ΔPe和Δph最后趋于0,ρ仅对p有影响,对其他2个输出影响可以忽略,实现了系统的解耦;从图5可以看出,当V1阶跃扰动时,仅有Pe变化量稳态值发生变化,其他2个输出值变化量稳态值为0,V1仅对Pe有影响;从图6中同样可以看出,当V2阶跃扰动时,仅有ph发生变化,V2仅对ph有影响。上述结果分析可知,加入解耦器后,系统的3个通道都实现了解耦。

图4 ρ阶跃扰动下输出参数特性Fig.4 Output parameter characteristics under ρ step disturbance

图5 V1阶跃扰动下输出参数特性Fig.5 Output parameter characteristics under V1 step disturbance

图6 V2阶跃扰动下输出参数特性Fig.6 Output parameter characteristics under V2 step disturbance

4 解耦控制系统仿真验证

根据单位阵解耦方法,在Matlab/Simulink仿真平台搭建解耦控制系统,结构如图3所示。在解耦器前分别加入一回路系统、二回路系统以及供热系统的PI调节器,3个PI调节器分别用于控制p、Pe、ph至其设定值,形成闭环系统,而解耦网络用于系统的解耦。分别在60 s时将p设定值阶跃增加0.1 MPa,Pe设定值阶跃降低10%,ph设定值阶跃降低0.1MPa,得到未解耦与解耦的输出响应如图7～9所示。

图7 p设定值扰动的输出响应Fig.7 The output response of p set value disturbance

图7中可以看出,p设定值扰动时,未解耦系统中,压力偏差导致控制棒的下插导致核功率下降;电功率由主调阀快速控制,因此压力变化引起的变化可以忽略;压力增加会导致进入供热系统蒸汽流量增加,从而影响用户侧压力先增加,后经调阀的调节达到设定值。对比解耦与未解耦的输出响应,p的超调量从35%降至没有超调量,调节时间不变;从M57.0%(2,1)可以看出,ρ对Pe几乎没有影响,因此解耦前后Pe没有变化;通过解耦器后ρ引起的ph增量比其他2个输入引起的变化要小,因此ph呈现先减小的趋势,超调量比未解耦时要小。

图8中可以看出,Pe设定值扰动时,未解耦系统中,电功率偏差导致控制器快速响应动作,主调阀开度减小;主集管压力增加,控制棒动作降低核功率从而控制其在设定值;进入供热系统蒸汽流量增加,其用户侧压力先增大再被控至设定值。解耦控制系统中,V1发生变化,p变化曲线的超调量解耦后降低为未解耦的一半;M57.0%(2,2)大于0.7,V1对Pe不受其他2个系统回路的影响,因此解耦前后差别不大;ph变化曲线超调量变化不明显,调节时间从600 s降低为327 s。

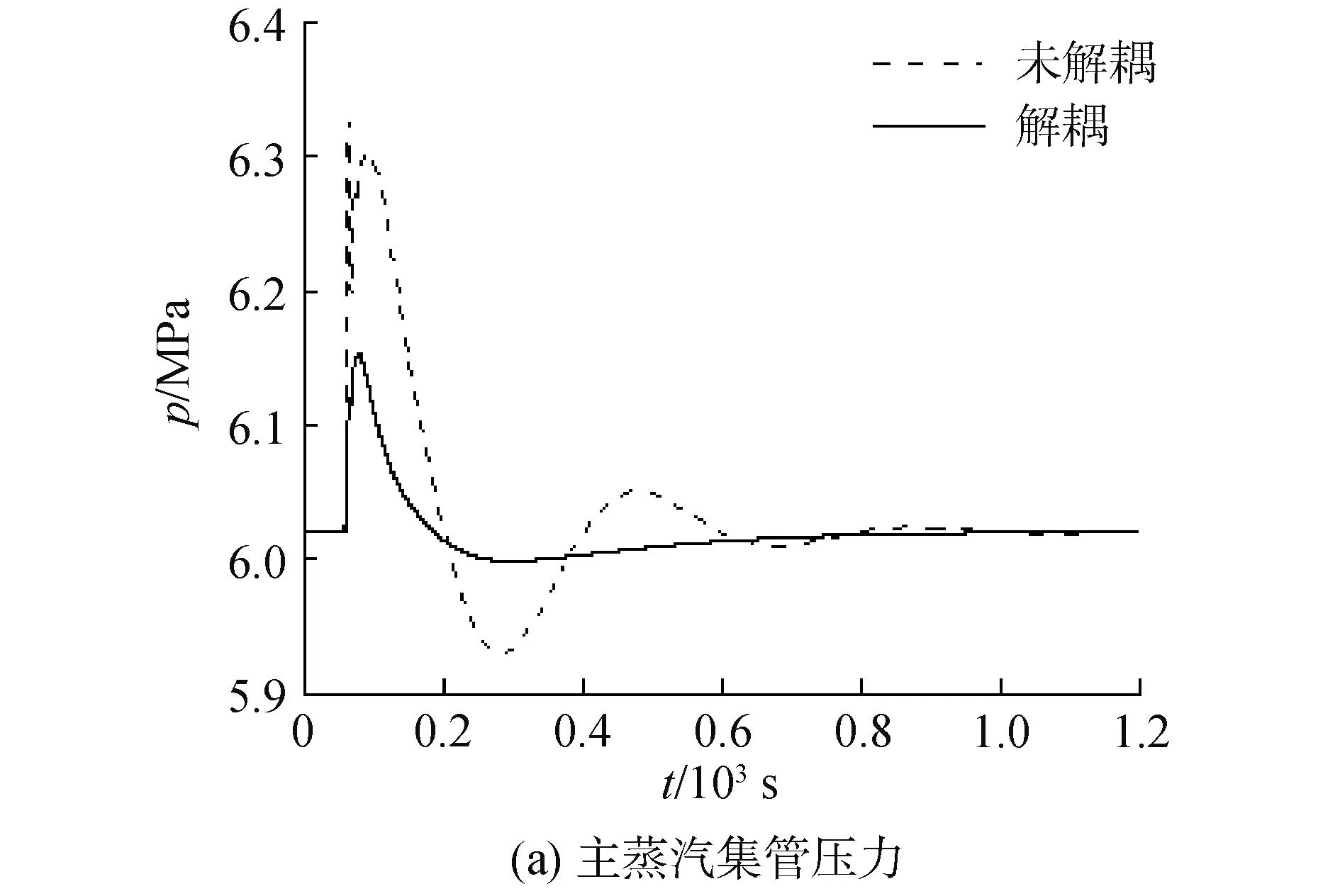
图8 Pe设定值扰动的输出响应Fig.8 The output response of Pe set value disturbance

从图9可知,ph设定值扰动。未解耦时,用户侧压力扰动导致控制器动作,供热调阀开度减小控制其至设定值;供热调阀的减小导致主集管压力升高,控制棒动作降低核功率,进而影响主集管压力变化;进入汽轮机的蒸汽流量增加,因此电功率先上升,然后被主调阀控制至其设定值。而解耦控制系统中,受解耦控制器的影响,p的超调量降低至未解耦的1/3;因为V2对Pe影响较小,所以Pe解耦前后没有变化;ph超调量从8%降至4%,而上升时间变长,调节时间几乎不变。