基于SANA实验的三维热工分析程序计算验证
2024-01-08张向丞佘顶陈福冰石磊
张向丞, 佘顶, 陈福冰, 石磊
(清华大学 核能与新能源技术研究院, 北京 100084)
球床式高温气冷堆是一种具有第4代核能系统特征的先进反应堆,其固有安全性能够确保在各种事故工况下,堆芯的燃料最高温度不会超过设计限值,从而避免大量放射性泄漏[1]。二维系统分析程序THERMIX和TINTE等被广泛应用于高温气冷堆内的热工分析,但这些程序的建模和计算都是基于二维的圆柱对称假设,难以处理高温气冷堆内存在的由于功率分布不均匀或几何结构不对称引起的三维热工问题。因此,开展针对球床式高温气冷堆的三维热工水力分析十分必要[2]。商用流体动力学计算软件如FLUENT和CFX等可以应用于球床高温气冷堆的局部三维热工水力分析,但全堆建模的时效性、复杂性以及难以与中子动力学计算程序进行耦合等问题仍然存在。因此,开发能够实现全堆快速三维热工计算的系统分析程序对于下一代高温气冷堆的设计工作具有重要价值[3]。
二维热工分析程序DAYU2D在吸收THERMIX软件包的基础上开发。基于该程序框架,本文根据堆芯内部的守恒方程和适用于球床式高温气冷堆的相关经验关系式,建立了三维热工水力计算模型,开发了三维热工分析程序DAYU3D,并针对德国SANA基准实验的部分工况进行了计算分析,验证了程序的计算功能。
1 DAYU3D程序三维热工分析模型
DAYU2D程序是由清华大学核能与新能源技术研究院开发的二维热工分析程序,用于分析球床式高温气冷堆热工水力特性。该程序采用了THERMIX程序中验证过的模型,包括固体材料和冷却剂的守恒方程以及材料的物性等。目前,DAYU2D程序已经完成了HTR-10和HTR-PM的稳态和瞬态算例验证,取得了良好的效果。在该程序框架下,本文开发的DAYU3D从基本守恒方程出发,在三维柱坐标系下对守恒方程进行简化、离散,结合球床传热及流动的经验关系式,建立了三维热工计算模型[4]。
1.1 三维热传导计算模型
球床中的固体区域能量守恒方程,考虑体积为dV的控制体,可以表示为:
(1)
式中:下标s为固体;cv,s、Ts、qn、λeff,s、qk分别为固体的定容比热、温度、核热源密度、球床等效导热系数以及通过对流换热进入到控制体的热量率,其中λeff,s由Zehner-Schlünder关系确定[5]。
图1为固体节点(I,J,K)处的计算网格划分,在对上述方程进行离散时,空间上采用了中心差分格式,时间离散选用后向差分,差分网格的边界则由周围的材料网格的体积中心连接构成,待求解的固体温度位于材料网格的端点。
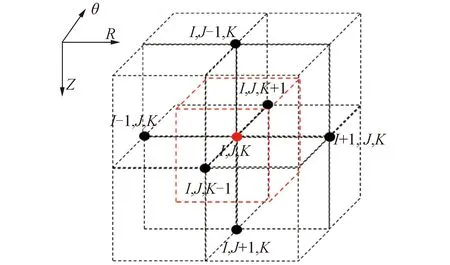
图1 固体节点(I,J,K)处的差分网格Fig.1 Differential grid at solid node (I, J, K)
由于球床在进行热工分析时是被视作各向同性的多孔介质模型,因此相较于二维模型,三维热传导计算模型只需多考虑周向上的热量传递[6]。
1.2 三维对流计算模型
气体相关参数的求解采用多孔介质模型,并且假设气体为理想流体,吸收的热量均转化为焓,满足h=cp,gTg。可得关于流体的能量守恒方程:
(λeff,gΔTg)+αF(Ts-Tg)
(2)
式中:下标g为气体;ρg为气体密度;cp,g为定压比热;Tg为气体温度;v为气体的速度矢量;λeff,g为气体有效导热系数;α、F分别为气体和固体间的对流换热系数以及对流换热面积。
气体的质量守恒方程可以表示为:
(3)
式中G为气体的质量流密度,矢量。
球床内气体的动量方程为:
(4)
式中:ui为气体速度在不同方向上的分量;μ为扩散系数;P为流体区域的压力;Rxi为对应方向上由经验关系式确定的流动阻力;γ为用于确定不同方向是否存在重力加速度的变量。左侧2项分别为非稳态项和对流项;右侧5项分别为动量扩散项、压力梯度项、粘性项、由于流固摩擦引起的压力损失项以及重力项[7]。
结合准稳态假设以及球床压降公式,球床内气体的动量守恒方程为:
(5)
式中:R为由经验关系式确定的流动阻力,矢量,通过引入球床阻力系数的经验关系式,可得:
(6)
式中:ψ为球床的摩擦阻力系数;dk为燃料球直径;ε为球床孔隙率[8]。
气体温度场的求解在空间上同样采用中心差分格式,计算网格划分与固体计算网格划分一致,待求解的温度位于材料网格端点。在求解气体压力场时,差分网格与材料网格重合,待求解的压力值位于材料网格的中心处,待求解的质量流量位于网格边界上。
图2为程序的计算流程图,DAYU3D程序包含初始化模块、固体温度计算模块和对流换热计算模块等,这些模块的功能相对独立,通过程序内部的物理量传递实现耦合。在求解固体温度场时,程序将流体的温度场、对流换热系数以及功率分布等作为已知量,计算固体温度场。在进行对流计算时,同样将固体温度场作为已知条件来进行计算。

图2 DAYU3D计算流程Fig.2 Flowchart of the DAYU3D calculation process
2 SANA实验建模
SANA实验装置建成于20世纪90年代,是由德国于利希研究中心建立并用于研究球床高温气冷堆内的热量传递以及事故工况下的热传输和余热载出问题[9]。
2.1 SANA实验装置介绍
实验装置由直径1.5 m、高1 m的石墨球床、4个加热元件(1个中心热元件和3个径向加热元件)、顶部和底部绝热层以及钢壳构成。球床区域由约9 500个直径为6 cm的石墨球堆积构成,孔隙率约为0.41。3个径向加热元件在周向上均匀布置在半径50 cm处。球床内的热源通过4根加热元件进行提供,中心加热元件为内径22 mm,外径32 mm的石墨加热管,径向加热元件为内径10 mm、外径20 mm的石墨加热管,加热元件与球床之间由石墨保护管隔开。球床布置在一个圆柱形的钢制容器中,顶部与底部的绝缘材料用以确保大部分热量水平流经球床,在球床内部填充有惰性气体(氦气或氮气)来模拟球床高温堆的实际情况并且避免由高温引起的石墨腐蚀。实验装置如图3所示,SANA实验装置内的温度测量采用热电偶,分别布置在容器壁、顶部与底部绝缘层、加热元件保护管以及球床内部的不同高度[10]。

图3 SANA实验装置示意Fig.3 Schematic diagram of the SANA facility
利用该装置,于利希研究中心开展了在对称及非对称工况下的球床加热实验。在对称实验中,仅通过中心加热元件对球床进行加热,该工况下的热源分布满足二维轴对称假设,装置内温度场在周向上保持一致。采用气体He/N2填充,对称加热的实验工况如表1所示[11]。

表1 SANA对称加热实验Table 1 Symmetric heating experiments by SANA
实验装置的结构及温度测点布置如图4所示,在轴向高度为9 cm、50 cm以及90 cm分别布置了底部、中部以及顶部温度测点。

图4 对称加热实验温度测点布置Fig.4 Measurement points in the symmetric heating experiment
非对称加热实验中,球床由直径为60 mm石墨球堆积而成,采用气体He填充,中心与径向加热元件同时对球床进行加热,使得热源在周向上出现周期性变化,球床内的温度分布也因此呈现出三维效应,实验的详细工况如表2所示[12]。

表2 SANA非对称加热实验Table 2 Asymmetric heating experiments by SANA
对应的温度测点布置如图5所示,测点分别位于含径向加热元件以及无径向加热元件截面轴向高度50 cm处。

图5 非对称加热实验温度测点布置Fig.5 Measurement points in the asymmetric heating experiment
2.2 SANA装置建模
根据SANA实验装置的结构以及几何参数,建立了如图6的SANA实验计算模型,模型中的各部件几何尺寸、材料如表3所示。由于实验所使用的环形加热元件的内部材料并未在实验报告中给出,为了保证计算建模与实验装置结构的一致性,此处将中心加热元件简化为半径16 mm的圆柱形加热棒。图6中材料1为孔隙率约0.39的随机填充球床,在靠近内侧石墨保护管以及外侧钢壳处的填充率根据SANA实验报告分别定为0.22和0.52,径向宽度为30 mm,球床的等效导热系数由Zehner-Schlünder关系确定[13]。
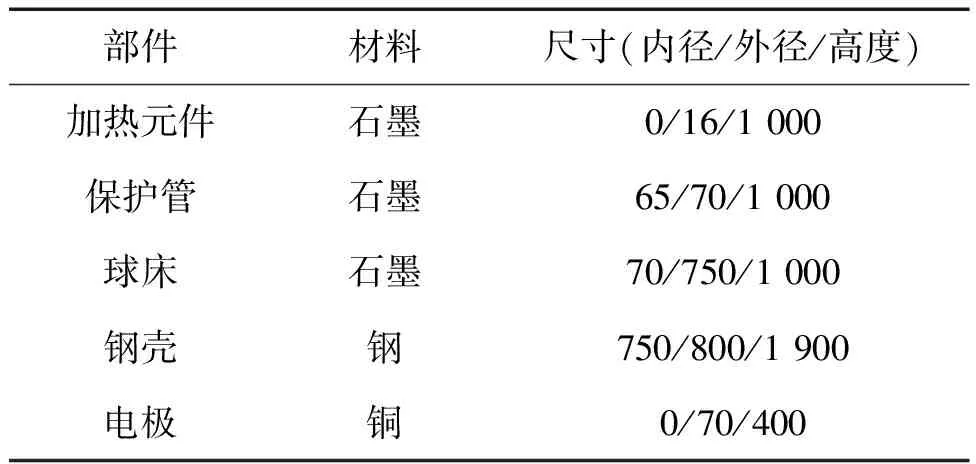
表3 SANA装置计算模型几何参数

注:1.中心球床,2.中心加热元件,3.保护管,4.顶绝热层,5~9.底绝热层,10.对流边界,11.内侧球床,12.外侧球床,13.电极,14.钢壳,15.石墨。图6 对称加热实验计算模型Fig.6 Model of the symmetric heating experiment
加热元件与保护管之间的热量传递主要通过热辐射进行,在DAYU3D程序中,热辐射模型被纳入到了等效导热系数的计算模型中,图6中材料15为发射率0.90的石墨材料。实验装置顶部及底部绝热材料的导热系数见文献[11]。
钢壳与外边界处的对流换热系数根据SANA实验报告[11]以及 Baggemann的研究[13]中给出的推荐值定为18.4 W/(m2·K),外边界温度为定温20 ℃。装置中加热元件的实际热功率约为额定功率的90%,计算中采用的热源密度为加热元件的实际热功率[14]。
对于非对称加热工况的计算模型,无径向加热元件栅元的材料网格划分与图6一致,包含径向加热元件的扇区的材料网格划分如图7所示,在距离装置中心50 cm处设置有径向的加热元件,程序在三维圆柱坐标系下进行建模,径向上的环形加热元件在模型中被等效为3个内径48.5 cm,外径51.5 cm,高度100 cm,θ方向栅元大小为4°的四棱柱加热区域,等效过程中保证径向加热区域的功率密度以及换热面积与径向加热元件近似一致。计算模型在径向划分了18个栅元,轴向划分了35个栅元,θ方向划分了24个栅元。
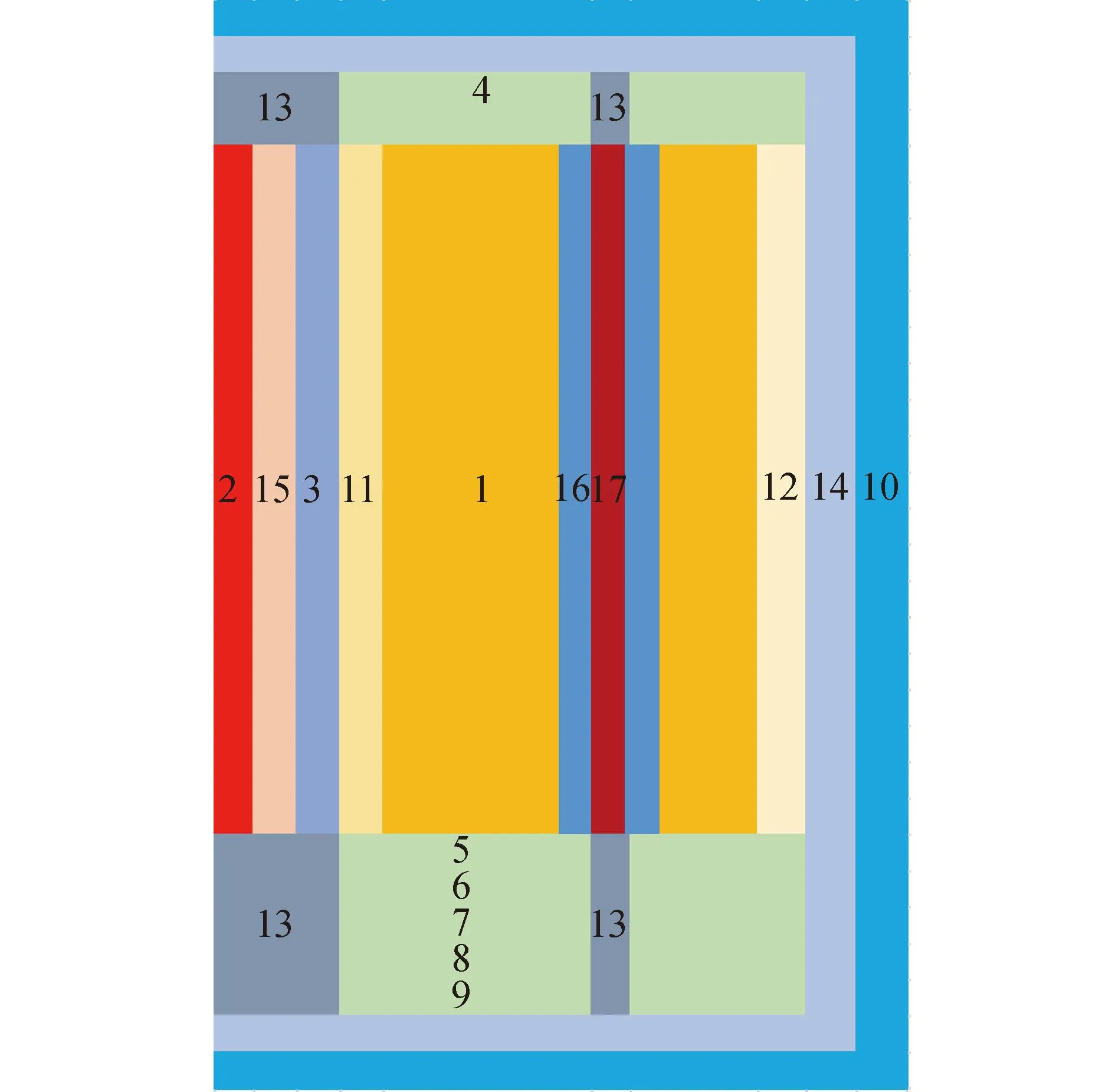
注:1.中心球床,2.中心加热元件,3.保护管,4.顶绝热层,5~9.底绝热层,10.对流边界,11.内侧球床,12.外侧球床,13.电极,14.钢壳,15.石墨,16.保护管,17.径向加热元件。图7 非对称加热实验计算模型Fig.7 Model for the asymmetric heating experiment
3 SANA实验结果模拟
3.1 SANA实验对称工况模拟
本文首先选择了大功率水平下的对称加热实验进行验证。在大功率水平下,自然对流对于计算模型的影响可以忽略,同时,更大的温度梯度有助于对模型存在的问题进行修正。因此,此处选择了30 kW中心加热、60 mm石墨球床、He作为保护气体的对称工况进行了模拟。
图8为30 kW功率水平下,不同高度处程序计算结果与实验测量值的对比。可以发现,两者总体上符合较好,计算误差在10%以内,计算得到的球床内部温度变化趋势与实验结果保持一致。随着半径的增大,球床的换热面积增大,导热系数随温度的降低而降低,在靠近对流边界出,球床温度变化趋于平缓,证明了程序对于球床内部的热量传递的模拟是可靠的。

图8 SANA装置30 kW对称加热实验计算结果Fig.8 Results for the symmetric heating experiment of the SANA facility at 30 kW
3.2 SANA实验非对称工况模拟
为了排除自然对流对于计算结果的影响,对于非对称工况实验,选取了表2中的第4组实验进行了计算,球床填充的惰性气体为氦气。同时,为了与DAYU2D进行对比,还将径向的热源在θ方向上进行平均,得到了均匀化处理之后的二维计算结果。图9为球床中部(Z=50 cm)不同截面处温度的计算值与实验结果的对比,其中,0°截面和60°截面分别对应图5含径向加热元件截面以及无径向加热元件截面。
在球床内部靠近加热元件区域,实验值略高于计算结果,这种差异主要是由于计算模型将加热元件近似为圆柱形加热棒,导致加热元件的功率密度略低于实际的功率水平。
从图9(a)可以发现,0°截面处固体温度随着向径向加热元件(R=50 cm)靠近,温度曲线先下降,随后开始上升,并在经过了R=50 cm处后,温度沿径向继续下降。60°截面处由于远离径向加热元件,温度并未出现明显上升,变化趋势与对称工况下的固体温度分布曲线类似。径向热源均匀化处理后计算得到的温度曲线介于0°与60°截面的温度分布曲线之间,与二者的温度相比均有明显的差异。
DAYU3D和DAYU2D程序计算得到的径向加热元件处的温度如表4所示,均匀化处理后计算得到的最高温度与实际温度823 ℃相差超过150 ℃,表明了三维效应对于球床温度的影响在功率水平较高的工况下不可忽略,二维均匀化处理对三维工况下球床的实际温度分布反映不够充分,处理球床高温堆中实际存在的三维热工问题存在困难。

表4 径向加热元件处温度Table 4 Temperature at the radial heating element
程序对SANA实验非对称工况的计算结果与测量值符合的较好,温度曲线的变化趋势接近,实验测量值均位于10%误差线内。在0°截面处,加热棒(R=50 cm)附近的温度值略低于测量值,这主要是由于模型将径向加热元件近似为四棱柱导致计算得到的功率密度小于加热元件实际的功率密度。在靠近侧面对流边界处,计算结果与实验值的差异主要是由边界处的对流换热系数的不确定性引起的。
4 结论
1)本文利用国际公开的SANA实验数据,验证了DAYU3D程序的三维热工特性分析能力。球床内的非均匀效应对内部温度场分布有重要影响。
2)相较于二维热工分析程序的均匀化处理方式,三维热工分析程序能够更精确地描述球床的热工特性,能更准确、合理的分析和评价真实球床高温气冷堆中的三维热工现象。
在实现了三维热工分析程序计算功能的基础上,后续还需开展更深入的工作,包括完善SANA计算模型加热元件的近似处理,对程序的功能开展更大范围的三维算例验证,与三维中子动力学计算程序耦合以探究三维热工程序在球床式高温气冷堆热工设计及安全分析中的应用等,为进一步提高高温气冷堆经济性和安全性提供支持。
