带螺杆轴心受压附着杆的整体稳定性

2024-01-08王斌郭兵李加敖

计算机辅助工程 2023年4期

王斌, 郭兵, 李加敖

(1. 山东建筑大学土木工程学院, 济南 250101; 2. 中建众力设备租赁有限公司, 济南 250101)

0 引言

建筑施工用塔式起重机(以下称为塔机)的高度较高,为防止侧向变形过大或发生倾覆,塔机的塔身独立高度有最大限值,一旦超过该限值,必须使用附着装置将塔身连接到建筑物上,以减少塔身的自由高度和受力情况,保证塔机的整体稳定性,提高运输能力。

塔机与建筑物的距离差别很大,建筑物的外形结构也不同,需要对附着杆进行单独设计,要求设置长度调节装置,通过螺杆调节附着杆的长度满足连接要求。但是,大多数塔机设计者在设计附着杆时,往往忽略调节螺杆对附着杆的削弱或者粗略地乘上一个安全系数,容易使附着杆的设计不安全、不经济,甚至发生附着杆失稳破坏,如图1所示。

图1 调节螺杆失稳破坏

近年来有众多学者对变截面压杆的临界载荷进行研究。杨立军等[1]和尹刚等[2]分别采用摄动法和加权残值法,得到变截面压杆弹性稳定临界载荷的解析表达式。卞敬玲等[3]在三维退化梁单元的基础上引入几何非线性,推导出计算任意变截面压杆稳定问题的有限元列式。彭攀[4]、谢海等[5]、刘建康[6]、陈玉骥等[7]和曹文贵等[8]尝试通过能量法,推导连续变截面压杆的稳定临界承载力表达式。齐舒等[9]以某钢桁桥的变截面箱形弦杆为原型,对轴心受压杆进行模型试验,同时采用有限元法对压杆失稳过程中的变形、应力和破坏形态进行分析研究。王欣等[10]和侯祥林等[11]分别通过NEWTON迭代法和VB设计程序,对多阶变截面压杆临界载荷方程进行求解。

以上研究针对的都是渐变截面或者截面惯性矩变化不大的突变截面杆件,带螺杆附着杆截面突变幅度很大,且螺杆长度占比较小,目前还没有针对这类杆件的设计方法。

带有螺杆的附着杆截面局部有突变,屈曲载荷降低,附着杆稳定验算时,可以将附着杆视为等截面杆件,但计算附着杆长细比时应乘以计算长度系数μb(该值大于1.0)以考虑调节螺杆的不利影响,因此需要给出计算长度系数μb的取值方法。本文通过4个螺杆占比不同但总长相同的试件进行轴压试验,记录加载过程中试件的挠度变化以及破坏形态,并使用有限元法进行对比分析,验证有限元模型的可靠性。通过有限元分析,研究各参数与杆件稳定极限承载力之间的关系,同时给出一定工程条件下计算长度系数可靠的取值方法。

(1)

式中:PE为压杆失稳的欧拉临界载荷;μ为杆件的计算长度系数;μ1为与杆件边界条件有关的计算长度系数(两端铰接时取1.0);μb为杆件变截面产生的计算长度系数;l为杆件总长度。

1 试验概况

1.1 确定研究参数

带螺杆的附着杆示意见图2,其为两端铰接轴心受压。影响这种杆件极限承载力的参数[12-17]主要有左段无螺杆段杆件长度la、螺杆的长度lb-la、杆件的总长度l、左段无螺杆段的惯性矩Ia、螺杆的惯性矩Ib以及右端耳板的惯性矩Ic。

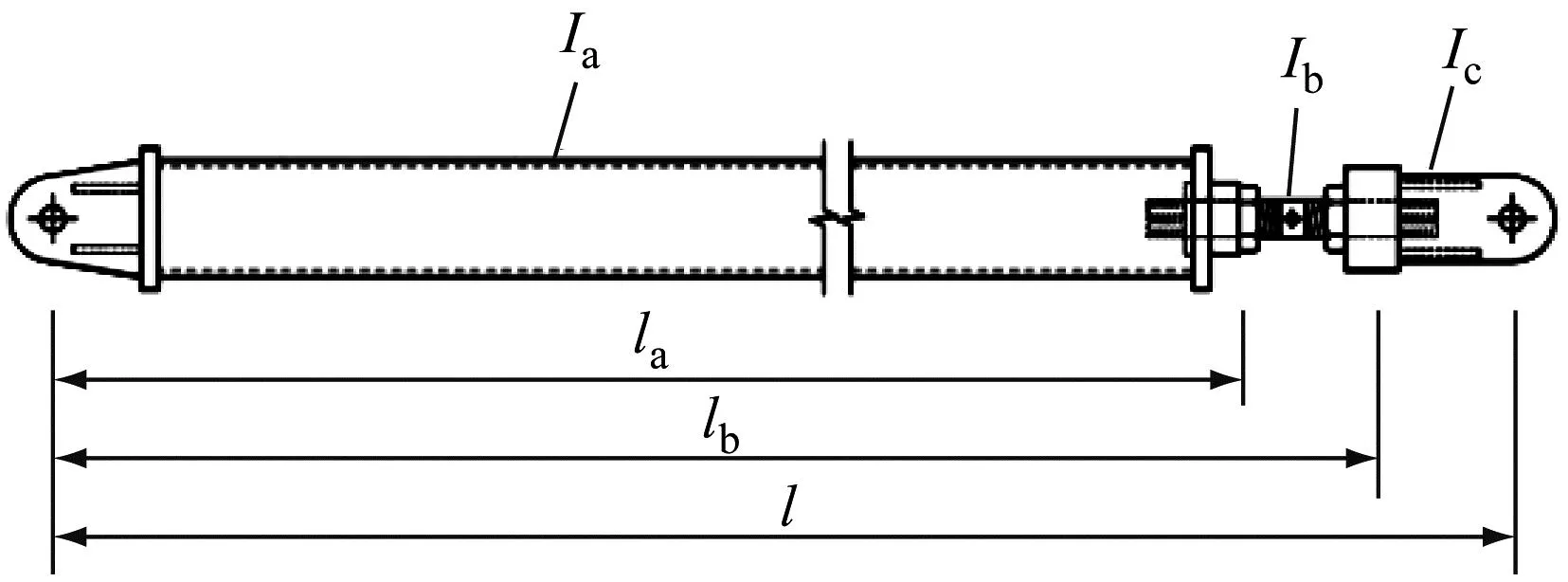
(a)详图

考虑以上所有参数,突变截面杆件极限承载力的影响参数过多,分析过于复杂,本文根据工程实际情况,对参数进行简化。在钢结构轴心受压整体稳定问题中,一般是杆件中心先发生失稳。杆件中心处因微小变形而产生的轴力附加弯矩(M=Py)最大,越靠近杆件端部,轴力附加弯矩越小,端部轴力附加弯矩为0,因此越靠近杆件端部,杆件因截面变化而对整体稳定承载力产生的影响越小。

因工程中需要满足构造要求,同时方便工人施工(转动调节螺杆调节杆件长度,满足塔机与建筑物的连接要求),塔机附着杆两端的耳板长度较短,位于杆件端部,且截面惯性矩远大于调节螺杆,对整体杆件的影响很小,故忽略两端耳板截面变化对整体杆件的影响。设计时,耳板截面及长度符合设计要求即可,也就是认为调节螺杆靠近端部且初始位置固定,l-lb为定值,且调节螺杆毛截面面积不小于附着杆毛截面面积。

1.2 试件设计与制作

考虑螺杆长度占比对杆件整体稳定承载力的影响,设计4根圆管附着杆(见图3),其中3根带有调节螺杆。这4根试件材料相同,圆管截面均为Φ114 mm×6.2 mm,调节螺杆直径均为62.5 mm,无螺杆段截面惯性矩与调节螺杆截面惯性矩为定值。

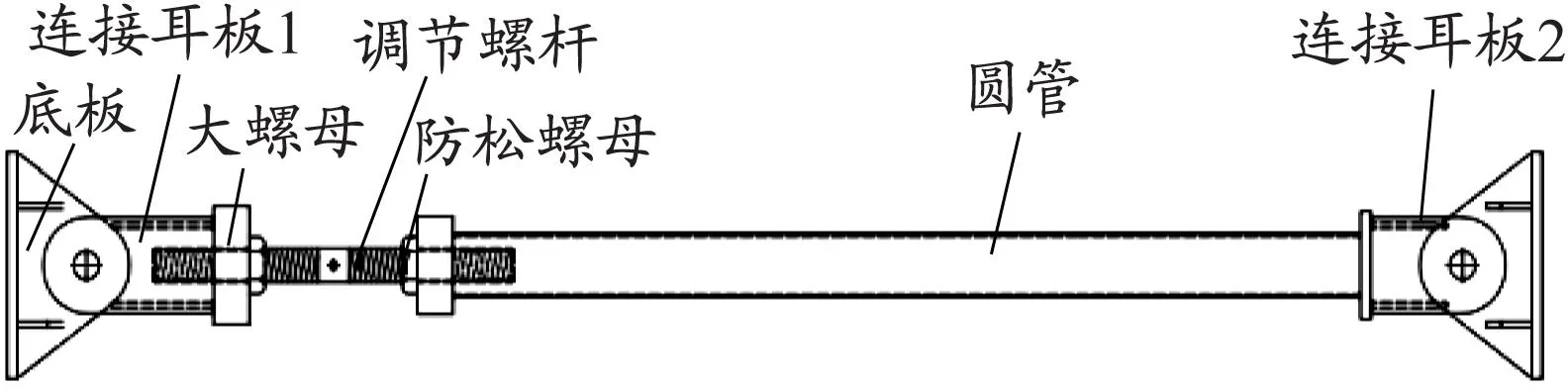
图3 带螺杆圆管的附着杆示意

耳板与底板连接示意见图4,通过销轴进行连接,以此提供两端铰接的边界条件。耳板及圆管与大螺母的连接方式均为焊接,螺杆通过螺母与杆件连接,通过转动调节螺杆实现杆件的伸缩,待调节好试件长度后通过拧紧防松螺母来固定试件的长度。4根试件的详细参数见表1和图5。

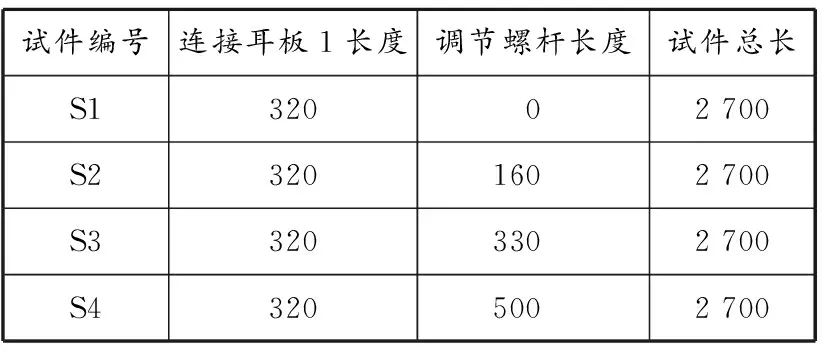
表 1 试件参数 mm

图4 耳板与底板连接示意

(a)S1

1.3 材性试验

试验所用钢材参照《金属材料室温拉伸试验验方法》,将圆管和调节螺杆切割成样条,使用微机控制电压伺服拉伸试验机(见图6),测得圆管和调节螺杆的应力-应变曲线(见图7)。钢材力学性能指标见表2。

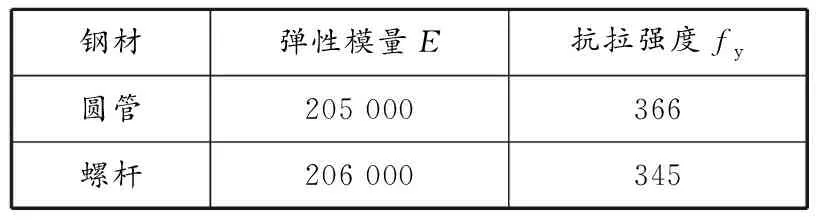
表 2 钢材力学性能指标 MPa

图6 拉伸试验机

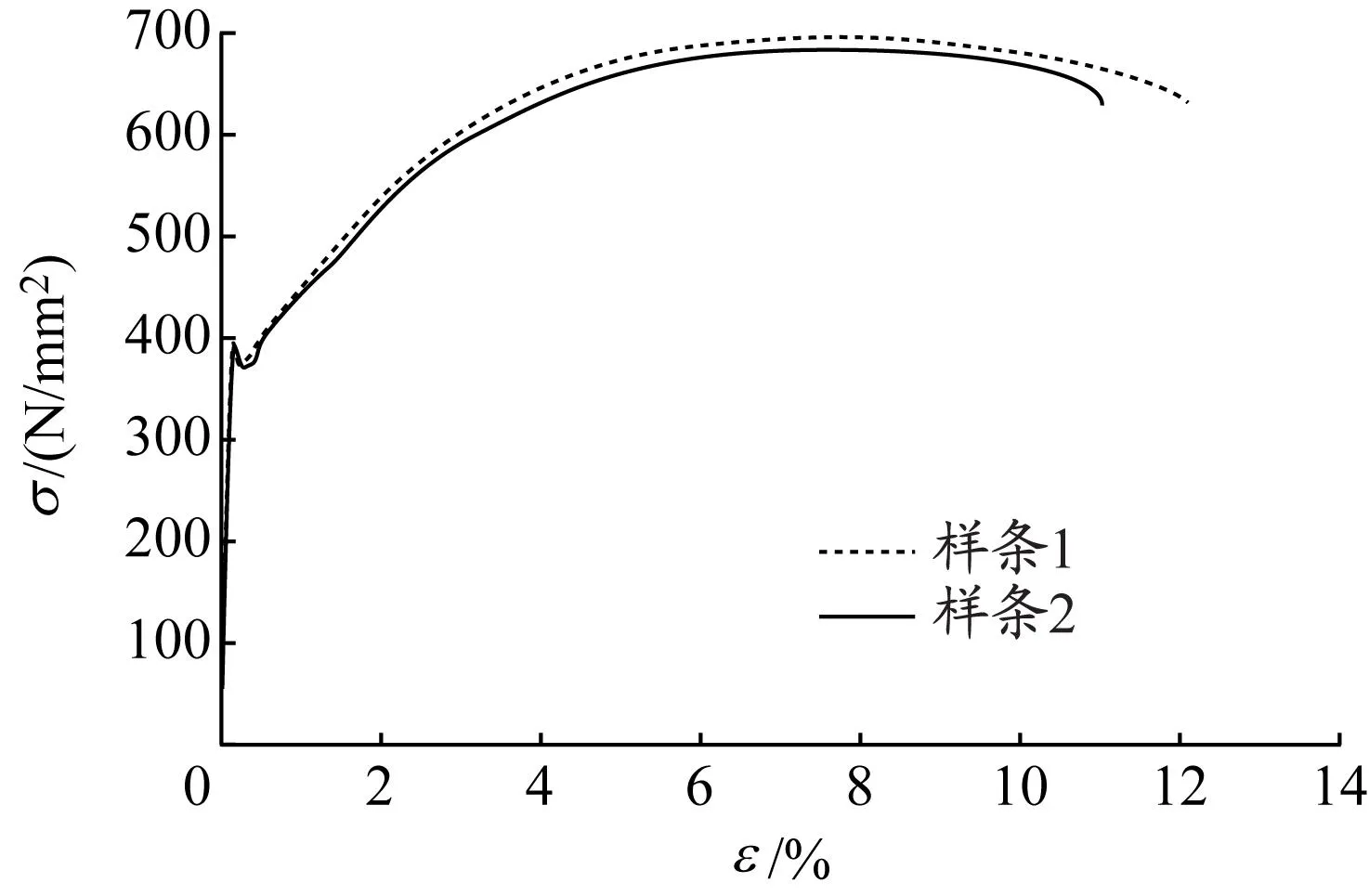
图7 螺杆材料应力-应变曲线

1.4 试验设备及加载方式

试验使用微机控制电液伺服5 000 kN压力试验机(见图8)加载,将压力试验机上部球铰固定,确保试验时试件各个方向均匀受力。

图8 试验加载设备

为监控试件在试验过程中的应力、应变情况以及进行物理对中,在预估的最大挠度处布置4个竖向的应变片。试验开始后全程采用位移加载,即通过油缸的竖向位移对试件施加载荷,其优点在于试件发生失稳破坏后设备会进行自动卸力并继续加载,便于采集载荷位移曲线后半段数据。加载速率为1 mm/min,至试件载荷下降到极限载荷的50%后停止加载。加载过程中使用设备自带的记录装置测量记录试件竖向位移及对应的承载力,记录并观察试验现象。

1.5 试件对中及初始缺陷

为保证杆件两端均为中心受压,尽可能减少初始偏心带来的影响,使用水准仪几何对中(见图9)并配合应变片进行物理对中。利用水准仪几何对中可以确保2个底板、试件截面形心、2个销轴以及压力机中线在一条竖向轴线上。应变片物理对中是在正式开始试验前,对试件进行预加载,加载的载荷值为20%的预估极限承载力,此时记录应变仪4个竖向应变片的读数,控制4个读数相差在10%以内。初始缺陷通过水准仪测量以及应变仪读数计算确定,见表3。

表 3 试件初始缺陷

图9 水准仪几何对中

2 试验现象与结果分析

2.1 试验现象及破坏形态

4根试件的主要破坏形态都是轴心受压导致的整体失稳,平均在开始加载后10 min左右发生破坏,但根据螺杆长度和初始缺陷的不同,发生整体失稳的位置和形态也不同。图10(a)为试件S1加载前的初始状态,是典型的等截面轴心受压杆;图10(b)为试件S1加载后的破坏图,屈曲模态为标准正弦。开始加载后,试件上的载荷随着油缸竖向位移的增加而增加,试件未见明显变形;加载至极限载荷时试件出现肉眼可见的侧向弯曲,已不适合继续承载;随着竖向位移的继续增加,试件出现较大侧向弯曲,同时承载力不断下降,试件中心发生较大偏移,发生弯曲屈曲,为典型的极值点失稳。

(a)加载前

试件S2加载前的初始状态见图11(a),加载后的破坏图见图11(b)。由于调节螺杆长度较短,试件S2的屈曲模态与S1相似,只是屈曲位置在杆件中心偏下处,破坏位置也在圆管上,变形由圆管侧向弯曲承担,调节螺杆未发生变形破坏。

(a)加载前

试件S3未加载的初始状态见图12(a),加载后的破坏图见图12(b)。开始加载后,随着油缸施加的竖向位移不断增大,试件产生慢慢发展的微小变形;加载至极限载荷后,调节螺杆中点处的侧向弯曲变形快速发展,试件开始卸力;随着竖向位移的继续增加,调节螺杆弯曲程度越来越大,此时圆管的侧向位移比试件S1、S2小,试件的侧向变形主要由调节螺杆承担,破坏后的调节螺杆见图12(c)。

(a)加载前

试件S4未加载的初始状态见图13(a),加载后的破坏图见图13(b)。开始加载后,随着油缸施加的竖向位移不断增大,因试件S4的初始缺陷非常小,试件调节螺杆处几乎未产生侧向位移;加载至极限载荷时,调节螺杆靠近圆管部位的侧向位移在短时间内急剧变化,试件几乎瞬间丧失承载力,杆件的侧向位移也主要由调节螺杆的弯曲造成,见图13(c),圆管几乎没有产生弯曲。

(a)加载前

2.2 试验结果分析

4根试件的竖向载荷-位移曲线见图14,试验的主要结果见表4。试件S1、S2、S3的初始缺陷大致相同,对比三者的极限承载力可知:试件S1承载力最大,此时试件没有设置调节螺杆;试件S2虽然设置调节螺杆,但螺杆部分长度很短且位于端部,对整个杆件稳定承载力的影响并不显著,极限承载力仅略低于未设置调节螺杆的情况;试件S3的稳定极限承载力最低,其调节螺杆长度较长,是杆件中的薄弱部位,对试件极限承载力产生显著的削弱作用,极限载荷相比未设置调节螺杆的情况下降15%。由此可见,调节螺杆对于附着杆极限承载力的影响不可忽略。

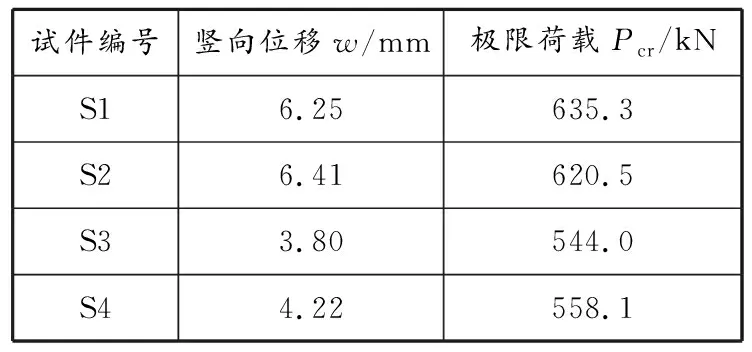
表 4 试验主要结果

图14 试件竖向载荷-位移曲线

从图14中还可以看出,试件S1、S2失稳时的竖向位移远大于试件S3、S4:这是由于试件S1、S2产生弯曲破坏的部位是圆管,能够产生较大的侧向弯曲变形;而试件S3、S4的侧向弯曲变形主要由调节螺杆承担,破坏时产生的侧向位移较小,故竖向位移较小时调节螺杆已经发生失稳破坏,导致试件达到载荷峰值的竖向位移较小。

试件S3、S4的调节螺杆发生弯曲变形的位置都靠近杆件中心,说明调节螺杆长度占比一定时,位置越靠近杆件中心,对杆件稳定承载力的影响越大。

值得注意的是,试件S4失稳后的侧向弯曲变形速度远快于另外3根试件。这是由于试件S4的初始缺陷相对于另外3根试件比较小,这也导致试件S4的极限载荷相近于试件S3,达到极限载荷后的卸载阶段,试件S4卸载速度也比其余3根试件快很多(竖向荷载-曲线后半段斜率最大),说明结构整体稳定对初始缺陷很敏感。

3 有限元分析及试验验证

以轴心受压带螺杆的附着杆试验研究为基础,使用有限元软件进行模拟分析。带螺杆的附着杆有限元分析模型见图15,模型单元采用C3D4实体单元,尺寸按照试件的实际尺寸,边界条件为两端铰接,螺杆与圆管之间为绑定连接。材料性质为各向同性,强度以及弹性模量按照试验的结果取值,材料为理想弹塑性,泊松比v=0.3。

图15 带螺杆的附着杆有限元模型

首先对模型进行特征值屈曲分析,其是考虑几何初始缺陷、几何非线性、材料非线性等影响因素后,实际杆件临界载荷的理论最大值,与截面惯性矩、计算长度、弹性模量和边界条件有关,与截面(格构式考虑换算长细比)具体形状无关。

通过特征值屈曲分析,可以得到杆件的欧拉载荷以及屈曲模态,计算得到试件的计算长度系数μb;再将屈曲模态按照试件的实际初始缺陷,施加到有限元弹塑性模型上,分析计算得到各个试件的稳定极限承载力Pcr,FE。各试件稳定承载力试验结果与有限元分析结果对比见表5,试件S3试验数据与有限元分析得到的竖向载荷-位移曲线对比见图16,破坏形态见图17。

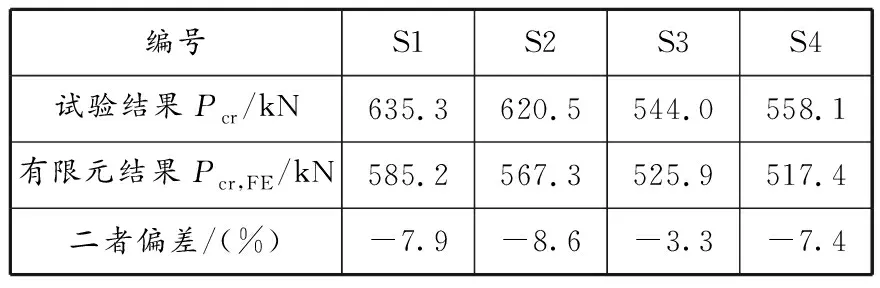
表 5 各试件稳定承载力试验结果与有限元分析结果对比

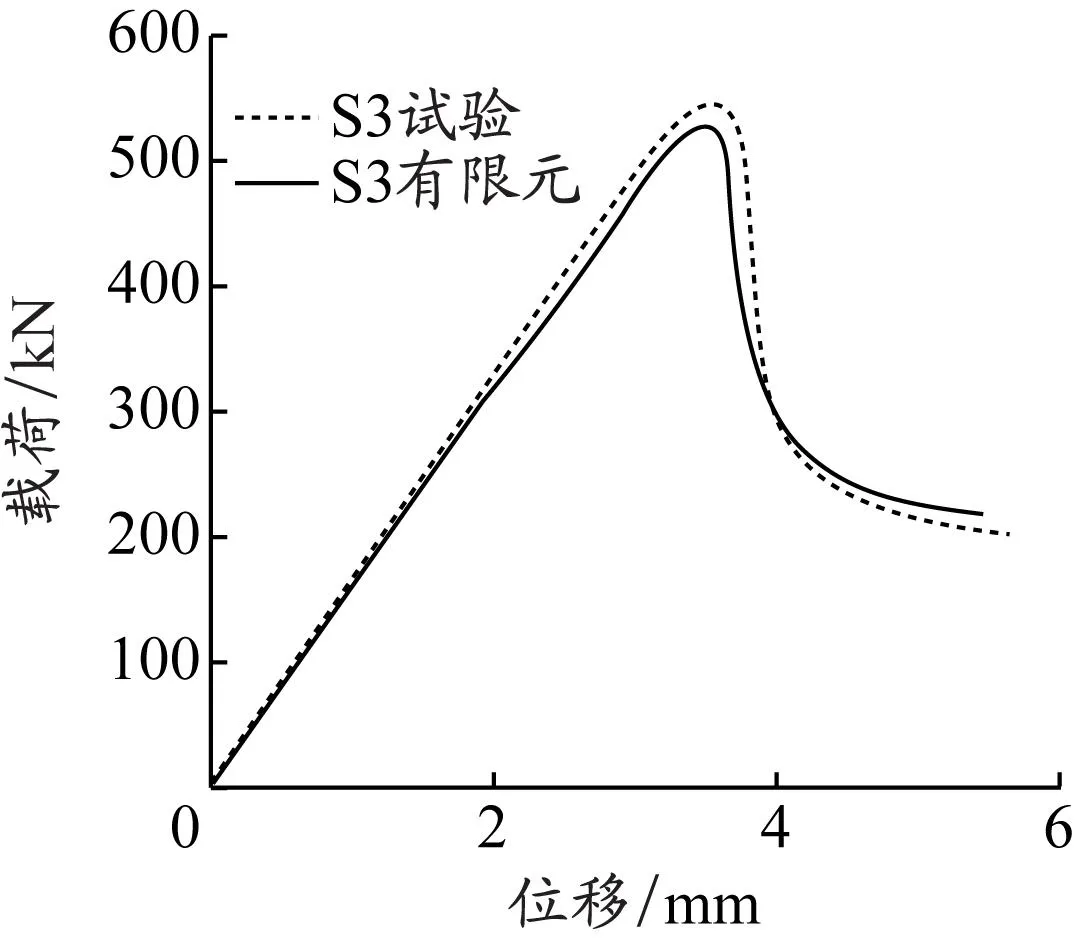
图16 试件S3竖向载荷-位移曲线对比

图17 试件S3破坏形态,kN

由图16可知,有限元软件模拟分析结果与试验结果吻合较好,二者误差在10%以内。因此,使用C3D4单元建立的有限元模型能较好地模拟带螺杆的附着杆轴心受压失稳破坏情况,可以在后续的参数化分析中进一步应用。

4 参数分析

为方便在工程中设计这种杆件,根据实际情况对一些参数进行常数化处理。耳板的长度根据连接销孔和螺杆直径确定,变化幅度不大,可定为330 mm;由于建筑物与塔机距离存在较大的不确定性,在附着杆安装前无法精确得到螺杆长度,一般在300～500 mm波动,因此按照最危险的情况将调节螺杆长度定为520 mm,可以满足绝大多数工程的构造要求。

在此基础上,将杆件分为有调节螺杆段l2(l2=850 mm)和无螺杆段l1(见图18)。通过大量有限元计算发现,无螺杆段长度与有调节螺杆段长度的比值l1/l2、无螺杆段杆件截面惯性矩与有调节螺杆截面惯性矩的比值I1/Ib是影响这类杆件稳定极限承载力的主要因素,故将l1/l2、I1/Ib定为主要影响参数。

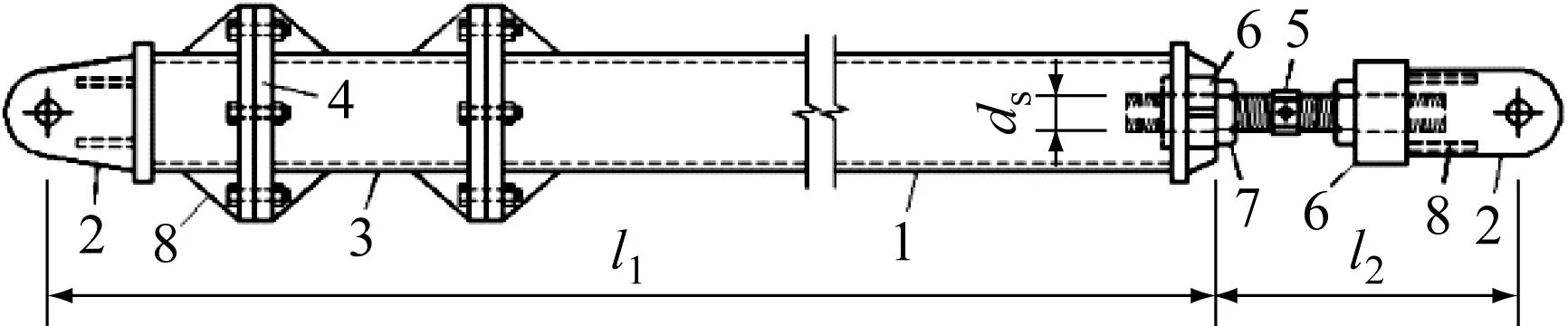
注:1—附着杆; 2—耳板; 3—接长段; 4—法兰; 5—调节螺杆; 6—连接螺母; 7—防松螺母; 8—加劲肋; l1—无螺杆段长度; l2—有螺杆段长度

为得到μb的值,使用有限元软件进行特征值屈曲分析。由于上文提到截面形式不影响特征值屈曲分析结果,截面形式对杆件稳定承载力的影响体现在稳定系数φ的取值上,因此可以取螺杆截面直径db=60 mm,l2=850 mm,其中螺杆长度为520 mm、耳板长度为330 mm(耳板截面满足设计要求即可),即l2和Ib为定值,通过变化l1和I1得到不同的计算结果。

根据实际工程,确定l1/l2和I1/Ib的取值范围为1

图19 l1/l2和I1/Ib对μb的影响

随机选取3个附着杆进行弹塑性稳定分析,最大初始挠度按(l1+l2)/1 000施加,附着杆材料均为Q235钢,螺杆采用45号工具钢,杆件信息及分析结果见表7和图20。可以看出,利用表6的μb查钢结构轴压杆件稳定系数表得到φ,根据GB 50017—2017[18]计算的极限承载力Nu=φAfy比有限元值均偏小,最大偏差9.9%,说明μb的取值方法可靠。表7可用于带螺杆的附着杆的设计和稳定承载力验算。

(c)载荷-位移曲线

工程中一般已知轴压设计值N、附着杆总长度l以及材料强度f(此处附着杆总长l为调节螺杆全部伸出时的长度),设计流程如下:(1)假定附着杆的长细比λ,查钢结构轴心受压杆件的稳定系数表得到φ,根据公式N=φfA可以确定附着杆的截面面积A。(2)由调节螺杆毛截面面积不应小于附着杆毛截面面积,确定调节螺杆的最小直径,保证选取的调节螺杆直径大于最小直径。(3)通过试算法,假设附着杆的截面惯性矩为I1,因l2=l-l1,根据l1/l2和I1/Ib,查表6并插值得到μb,找到合适的附着杆截面惯性矩,使得λ=μbl/i,根据附着杆的回转半径i以及A选取附着杆截面。