基于优化方法的燃料组件简化梁模型材料参数等效研究
2024-01-08冯璇郭严李康桥梁国鹏肖长江卢梦凯管官梅跃
冯璇, 郭严, 李康桥, 梁国鹏, 肖长江,卢梦凯, 管官, 梅跃
(1.大连理工大学 a.工程力学系; b.船舶工程学院,辽宁 大连 116024;2.中广核研究院有限公司,广东 深圳 518031; 3.宁波大学 机械工程与力学学院,浙江 宁波 315211)
0 引 言
堆芯燃料组件是核反应堆中的重要部件,在运行过程中受堆内辐照和高温影响,其材料呈现出复杂的非线性力学行为,使得燃料组件产生轴向、弯曲和扭转等宏观变形,给反应堆的安全运行造成一定影响。另一方面,整个堆芯内常有上百个燃料组件,每个燃料组件内部的结构数量繁多且相互装配关系复杂,若直接采用三维实体精细化建模方法对全堆芯进行仿真分析,则计算规模大且非线性程度强,很难得到收敛解。为此,研究一种快速高效且具有一定精度的计算仿真模型具有重要意义。
国内外许多学者提出很多燃料组件简化模型方案[1-9],如单梁模型、二梁模型、三梁模型、四梁模型等,但大多只给出简化建模方案和验证,并没有给出具体的材料参数等效方法或者给出的等效方法较复杂。其中,JEON等[7]研究的半精细化四梁模型的材料参数直接采用相关金属材料的属性,对梁模型仅进行几何截面的等效。虽然此方法可使全堆芯模型的建模和分析得到一定程度的简化,但因四梁模型本身内部结构相对复杂,将其直接应用到全堆芯建模和分析中仍费时费力。
在全堆芯尺度的计算中,往往更关注组件与组件之间的相互作用关系,因此可考虑将组件简化为建模更加简便的单梁模型。然而,直接从实体模型等效简化为单梁模型十分困难,故考虑从四梁模型到单梁模型的简化。
本文以文献[7]所研究的四梁模型为目标等效模型基础,建立更简化的单梁模型来等效整组件。主要考虑静力学等效刚度和动力学方面等效振动模态频率的方法,基于一定的假设、简化和优化方法算法,实现从相对复杂的二维半精细化四梁模型到三维简化单梁模型的材料参数等效,最后研究单梁模型之间的关系,建立单梁小堆芯模型。
1 简化建模
1.1 二维半精细化四梁模型
为尽可能地体现各主要零部件之间的相对关系,以提高计算结果的精确性,二维半精细化四梁模型建模主要考虑以下零部件:上管座、下管座、结构格架、燃料棒和导向管及其连接部件等。假设二维半精细化四梁模型长3 537.7 mm,宽141.5 mm,共建立8层结构格架,每层格架与导向管和燃料棒之间采用间隙单元与弹簧单元进行连接,以模拟实体模型中格架弹簧、刚凸等零部件。模型共包括122个节点、226个单元。二维半精细化四梁模型的结构及边界条件见图1。
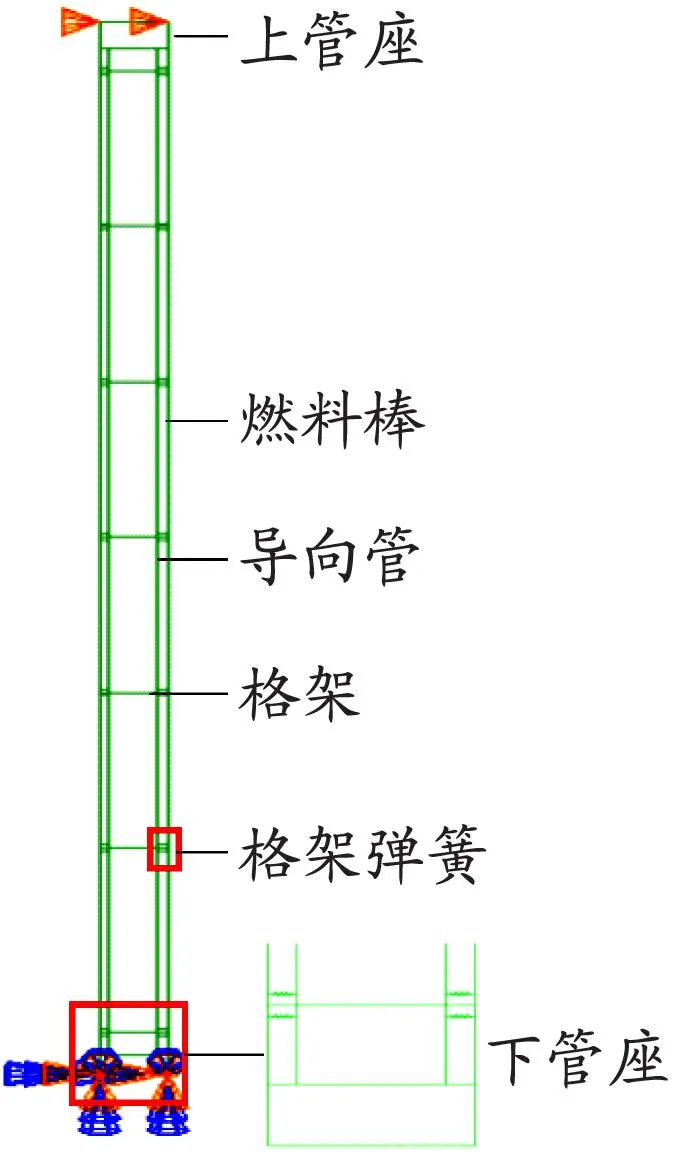
图 1 二维半精细化四梁模型的结构及边界条件
图1中,最外侧2根纵梁为实体模型中所有燃料棒的等效结构,内侧2根纵梁为实体模型中所有导向管的等效结构,横梁为每层结构格架的等效结构。其中,各梁单元几何截面均采用自定义型几何截面,通过计算不同部件三维实体几何模型截面面积、惯性矩等参数,赋予对应梁截面几何属性。
1.2 三维简化梁模型
在二维半精细化四梁模型的基础上,考虑到全堆芯模型建模的复杂性,建立尽可能简化且合理的三维模型。因此,有必要建立等效的单梁模型代表1个燃料组件。
为了方便建模,在对二维半精细化四梁模型到三维简化单梁模型进行材料参数等效时,暂不考虑组件与组件、组件与围板之间的碰撞。采用Timoshenko梁单元建立单梁模型,简化模型的结构和约束条件见图2,其长度和约束条件与二维半精细化四梁模型一致,截面采用矩形截面,尺寸与三维实体组件外围尺寸一致。

图 2 三维简化单梁模型的结构和约束条件
2 优化算法
通过优化算法,迭代计算出一致的加载点位移和振动频率特征值,来确定三维简化单梁模型材料等效参数。其静力平衡方程为:
通过以上的例子可以看出,由于不同语言造成的思维方式、文化习惯等差距的客观存在,使得若干原语中的某些文化或语言因素无法被译语国家读者容易理解。这使得这些寓言标题翻译面临困难。然而,译者抛开了固化的思维,根据具体实际采取某些恰当的翻译方法如省译法,增译法或者另立标题法对原语信息进行重新剪裁等处理,消融了不同语言和文化间的障碍,让原语读者和译语读者获得相一致的阅读效果,产生了相近甚至相同的阅读反应,实现了翻译效果的动态对等。
F=Ku
(1)
式中:F为外力;K为刚度矩阵;u为位移矢量。
振动方程为:
Kφ-w2Mφ=0
(2)
式中:w为固有频率;φ为特征向量;M为质量矩阵。
由于通过直接求解法很难找到最优解,因此本文将其转化为一个优化问题:即二维半精细化四梁模型与三维简化单梁模型在载荷边界条件一致的条件下,找到最佳的弹性模量E和密度ρ,使得2个梁模型有最接近的位移解和1阶振动频率特征值,其优化的数学模型如下:
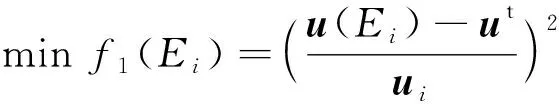
(3)
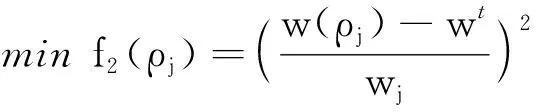
(4)
式中:ut为目标位移值;u为位移矢量;K为刚度矩阵;M为质量矩阵;f1和f2为目标函数。
为求解该优化问题,首先输入未知弹性模量参数的初始假设值,通过有限元法求解式(1),获得加载点挠度值,评估目标函数是否最小化;不断更新迭代,直到目标函数小于公差,输出弹性模量值;给定初始密度假设,并输入上一步输出的弹性模量值,通过有限元法求解式(2),获得振动频率特征值,评估目标函数是否最小化。如果目标函数最小化,那么输出计算结果;如果没有最小化,那么采用内点法更新优化变量。重复上述过程,直到目标函数小于公差,输出密度值。具体求解路线见图3。
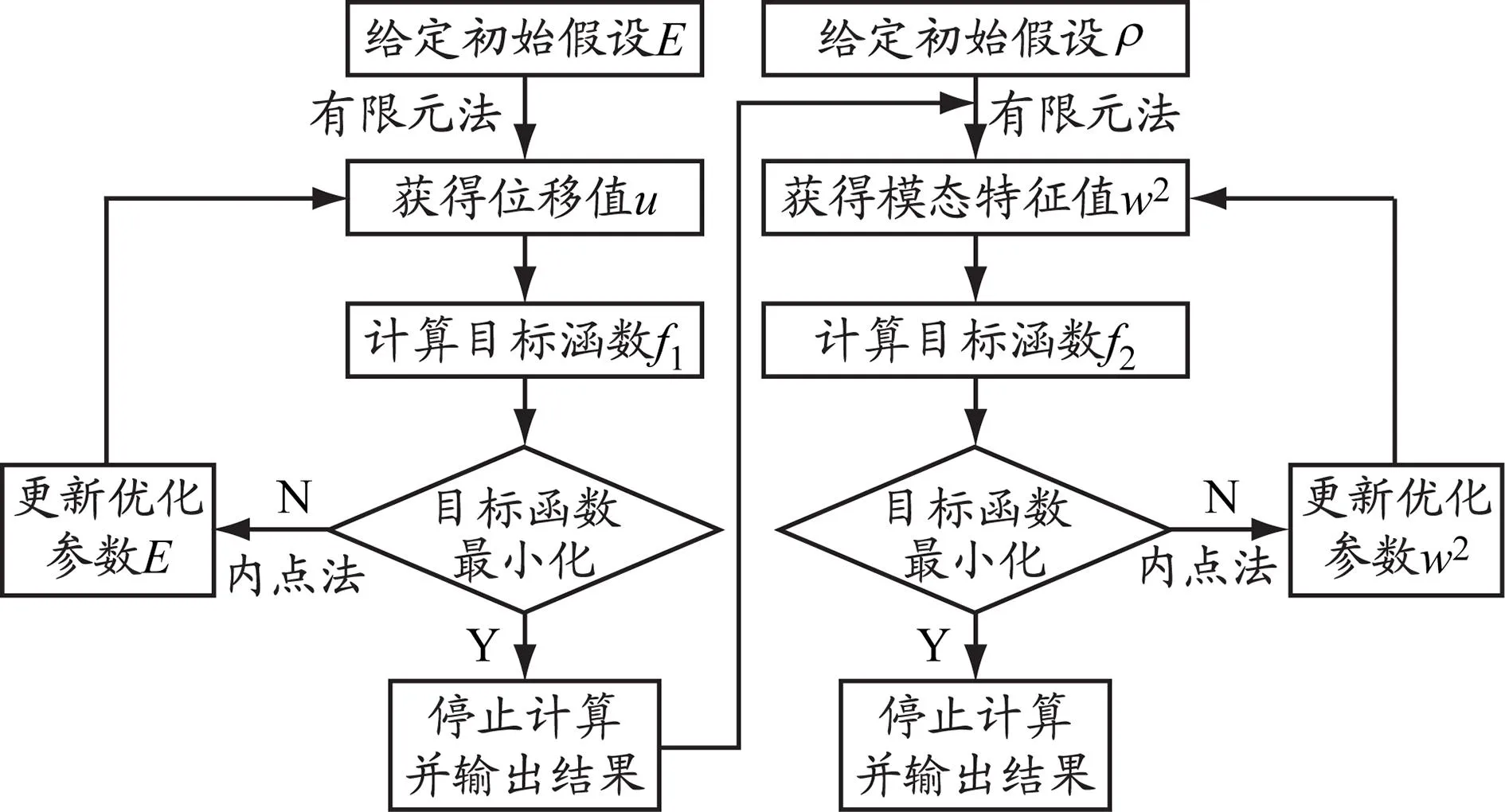
图 3 求解路线
3 算例分析
3.1 三维简化单梁模型刚度等效
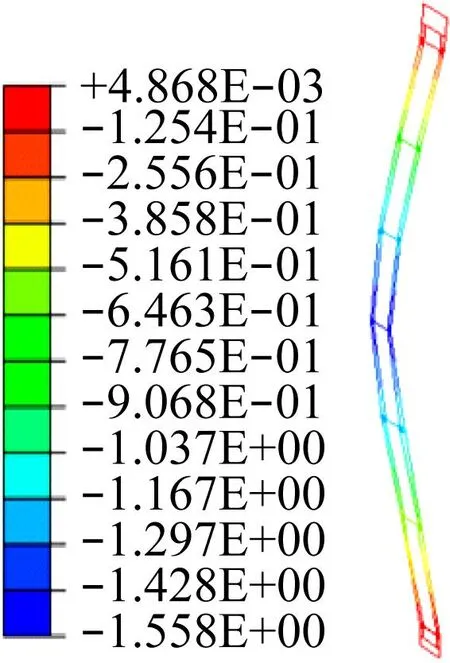
在已建立的二维半精细化四梁模型和三维简化单梁模型的对应位置处施加相同载荷,并按照实体模型的材料参数对二维半精细化四梁模型的对应部件赋予参数。提交计算二维半精细化四梁模型的位移,输出加载点位移数值作为优化参数。给定三维模型一个初始的刚度值,通过自编的优化程序不断迭代计算,直到求解出三维简化单梁模型刚度的最优解,并写入模型输入文件。将该输入文件提交计算,计算结果见图4。
(a)二维半精细化四梁模型
由图4可知,三维简化单梁模型使用等效出的弹性模量值进行计算,在加入相同的载荷边界条件后,2个模型的几何变形和位移数值基本一致,即三维简化单梁模型等效的刚度可取。
3.2 三维简化单梁模型密度等效
按照实体模型的材料参数,对二维半精细化四梁模型的对应部件赋予参数。将第3.1节得到的刚度值结果赋予三维简化单梁模型,并给定三维简化单梁模型一个初始密度值。通过自编的优化程序不断更新三维简化单梁密度值并迭代计算,直到使三维简化单梁模型与二维半精细化四梁模型有效质量较大的模态特征值差别最小。
模态有效质量是按照模态质量归一化后求得的模态参与因子的平方和,系统第i阶模态的模态有效质量[10]
(5)
式中:Li为模态参与因子。Li=φTMr,φ为结构模态特征值向量,M为质量矩阵,r为位移变换向量。
一般来说,结构模态越低阶,模态的有效质量越大。计算本文目标模型的1阶模态,其有效质量可达88.64%。因此,本文主要优化密度,使得2个模型的1阶模态特征值之差最小。在迭代计算得到最小1阶模态特征值之差时,输出三维简化单梁模型的密度最优解,并写入模型输入文件。将此输入文件提交计算,计算结果见图5。

图 5 1阶模态特征值云图
由图5可知,在相同边界条件下,三维简化单梁模型使用等效出的密度值进行计算,得到的1阶模态特征值与二维半精细化四梁模型的1阶模态特征值基本一致,即三维简化单梁模型等效的密度可取。
3.3 误差分析
定义相对误差
(6)
式中:λ3D为三维简化单梁模型使用优化得到的刚度和密度计算得到的加载点位移或1阶模态特征值结果;λ2D为二维半精细化四梁模型计算得到的加载点位移或1阶模态特征值结果。
代入数值进行计算,得到二维半精细化四梁模型和三维简化单梁模型加载点位移误差(见图6)及1阶模态特征值误差(见表1),二维半精细化四梁模型和三维简化单梁模型位移随高度变化见图7。
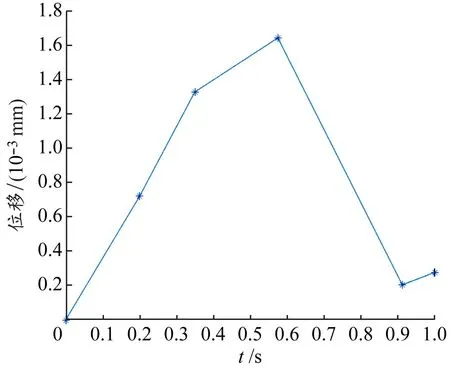
图 6 加载点位移误差
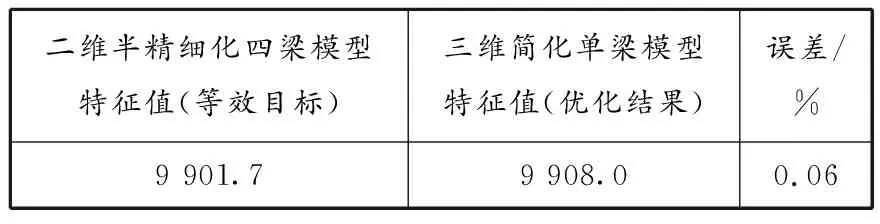
表 1 1阶模态特征值及误差
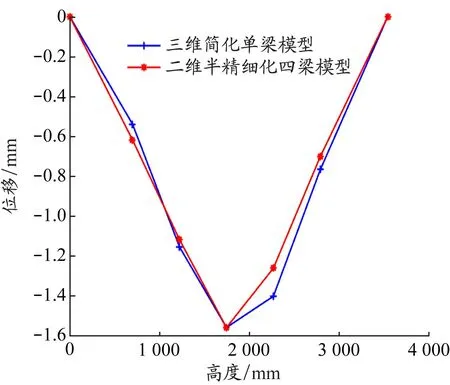
图 7 位移随高度变化比较
由图6、7和表1可知,三维简化单梁模型使用优化得到的刚度和密度计算得到的最终加载点位移和1阶模态特征值结果与二维半精细化四梁模型的等效目标结果误差均不超过1%。对于分析燃料组件的某些力学行为,三维简化单梁模型即可实现,大大降低建模的复杂性和计算量,对于全堆芯的建模及计算具有重要意义。
4 小堆芯有限元模型建立
在完成单组件简化梁模型等效分析的基础上,考虑到在实际运行中相邻燃料组件或燃料组件与堆芯围板的碰撞现象[11-12],本文进行单梁模型梁与梁之间联系的研究。燃料组件结构格架部分存在结构弹簧且组件之间的格架存在一定的小间隙,因此在建立小堆芯模型时考虑弹簧单元和间隙单元,见图8。图中,K和C分别为格架外刚度和阻尼;N为格架质点,为方便建模,本文取距格架外围1/4格架宽度建点;g表示间隙。
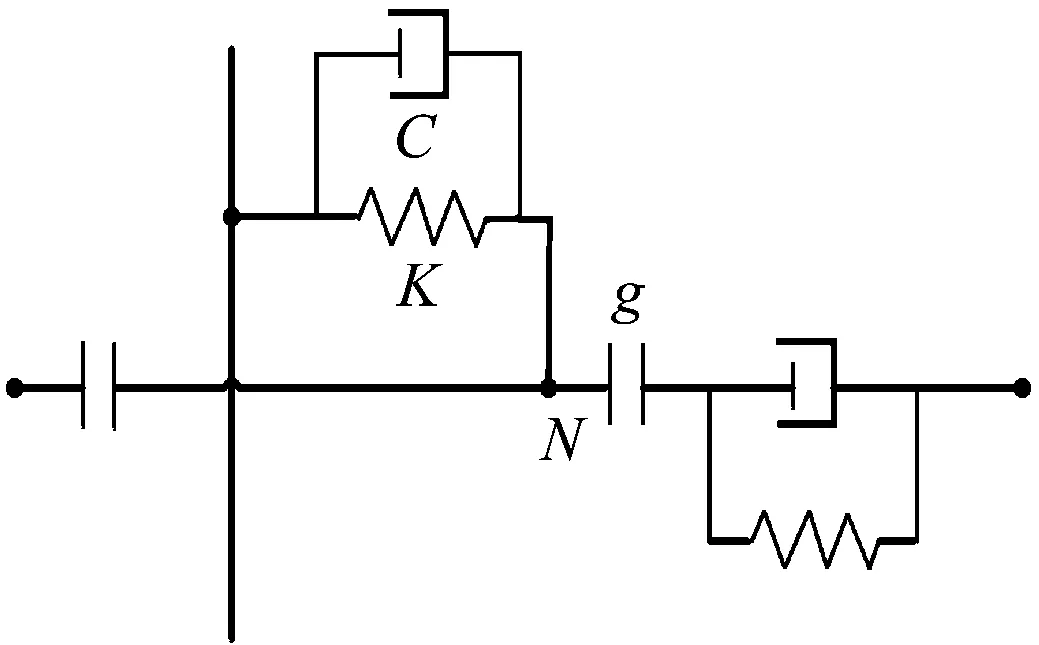
图 8 格架碰撞模型
按照本文方法进行3×3小规模燃料组件堆芯等效梁有限元建模,每根梁代表1个燃料组件,见图9。
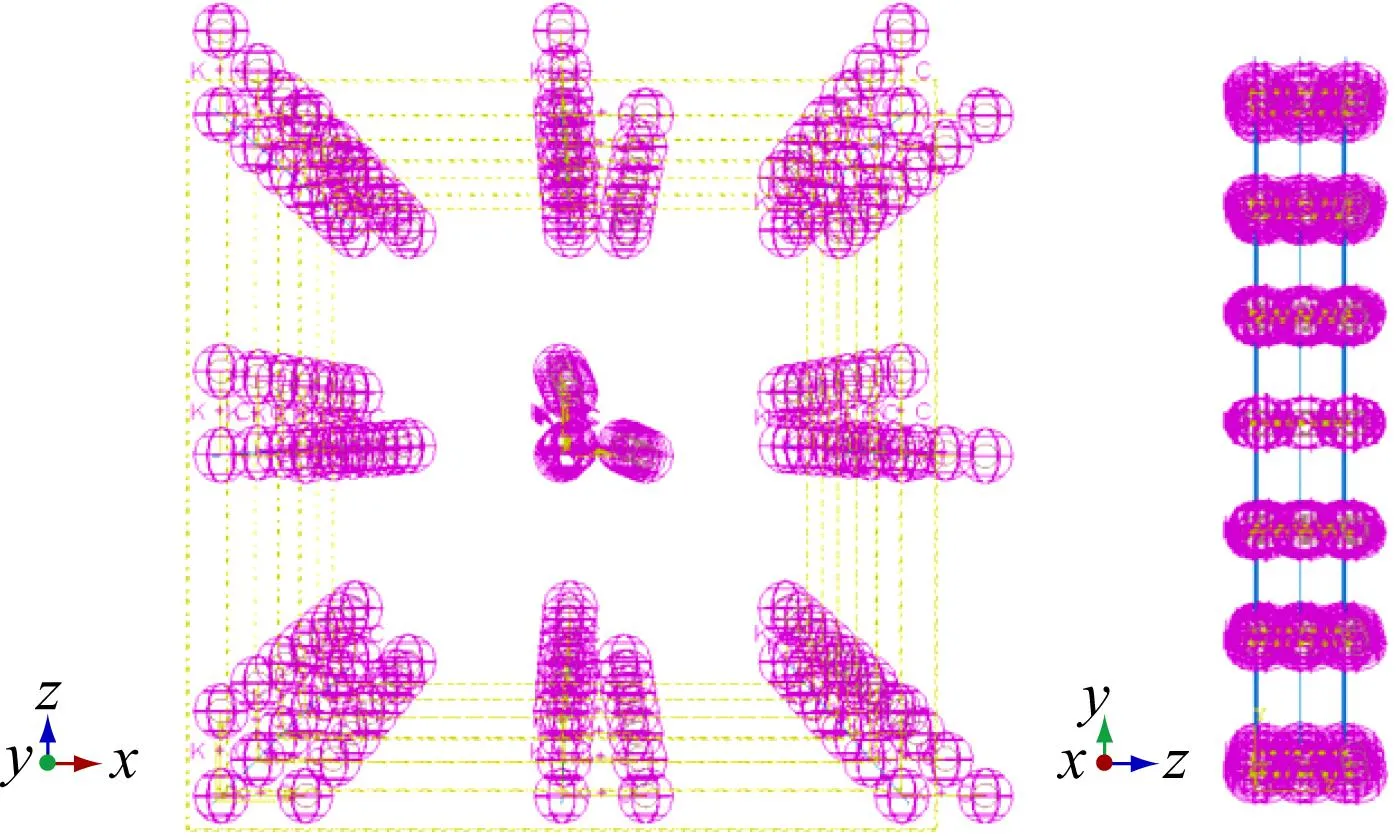
图 9 3×3小规模堆芯模型示意
建模完成后,对其进行适当的边界条件设置并在格架节点处施加x方向载荷,得到x方向的位移计算结果,见图10。由图10可知,对小规模燃料组件堆芯简化梁模型中的1个节点施加载荷后,载荷可以通过间隙单元和弹簧单元进行传递。结合单梁模型算例,本文方法在调整刚度等参数后,可以有效模拟全堆芯燃料组件,为全堆芯建模分析及简化模型等效参数设置提供新的思路。
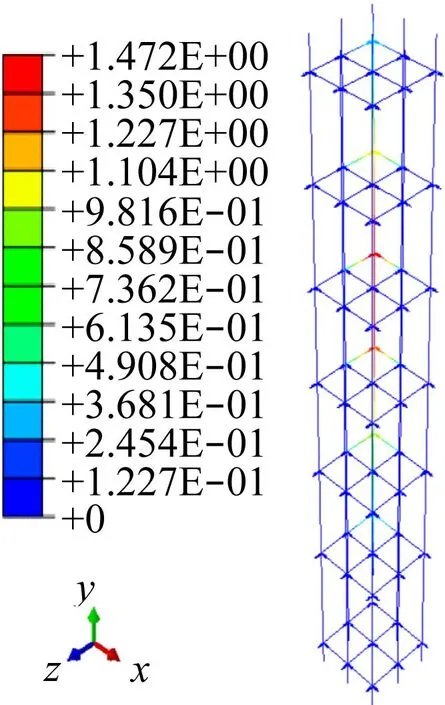
图 10 小规模堆芯模型加载后x方向位移云图,mm
5 结 论
采用有限元软件对二维半精细化四梁模型和等效的三维简化单梁模型,进行静力及模态分析对比,并开展小堆芯模型建立和试算,得出以下结论:
(1) 提出的优化方法能较准确地等效出燃料组件三维简化单梁模型的刚度、密度等材料参数。
(2) 对于全堆芯模型的建立和分析,采用单梁模型及碰撞连接模型建模更简单,能实现载荷传导和完成合理分析,为复杂模型的等效分析提供参考。
