飞机典型结构累积毁伤效应及毁伤机理
2024-01-07李元刘延春王晓光豆清波索涛
李元 刘延春 王晓光 豆清波 索涛*
(1 西北工业大学航空学院,西安 710072;2 西北工业大学极端力学研究院,西安 710072;3 中国兵器工业集团航空弹药研究院,哈尔滨 150001)
0 引言
自1911 年飞机作为武器投入战争以来,在战场环境下产生损伤的情况时常发生。飞机的战伤抢修逐渐进入人们的视野。1942 年太平洋战争,飞机战损与战伤比例为1:3。中东战争和马岛战争中,作战空军对大量战机在战时进行了修复。历史表明,战伤飞机数量远大于战损飞机的数量,对战伤飞机进行修复使其恢复作战能力具有重要意义[1]。而飞机在空中受到的主要威胁来自于战斗部爆炸产生的破片以及冲击波,故研究两种毁伤元的联合毁伤效应以及机理成为飞机修复的关键,也是当下研究的热点[2]。
T.Hatch-Aguilar 等人使用ALE3D 软件进行了模拟,研究了破片和冲击波对钛、铝和钢等不同材料靶板的影响。研究结果包括靶板在不同作用情况下的最大动量、动能、偏转、穿孔尺寸和塑性变形。然而,由于缺乏实验验证,研究未给出确定性结论,仅限于初步讨论破片和冲击波之间的耦合作用[3]。北京理工大的侯俊亮以雷达作为毁伤目标,将破片冲击波联合作用分解为破片穿孔效应和爆炸冲击波对穿孔后平板的冲击作用两部分,建立了冲击波的工程模型、预制破片初速修正模型、在空气中的衰减模型及破片穿孔模型。以有孔平板相对于无孔板的挠度变形增量来表征联合毁伤效应[4]。南京理工大学的刘刚研究了破片和冲击波对直升机旋翼及机身的联合毁伤,通过对旋翼结构进行分析和等效,通过赋予破片初速度和CONWEP爆炸模型模拟冲击波的方法,对旋翼在破片和冲击波联合作用下的毁伤过程进行了计算,分析了联合作用下的毁伤增益效应。但未用实验进行相关验证[5-6]。Shengrui Lan 等人使用高保真物理的有限元分析技术进行了数值模拟,并通过拟静力试验、爆炸荷载试验和破片与冲击波联合作用试验对模型和模拟技术进行了验证。研究还评估了全尺寸钢筋混凝土板在联合作用下的动力响应以及受损板的剩余承载能力[7]。南京航空航天大学的董秋阳等人针对破片和冲击波复合作用下的结构损伤,利用LS-DYNA 软件,建立了机翼蒙皮在破片和冲击波单独作用及复合作用下的损伤模型。通过分析计算结果,研究了蒙皮的损伤机理、损伤形式和损伤程度。针对破片和冲击波的联合作用,研究了破片速度、冲击波峰值超压和正压区作用时间对蒙皮损伤的影响。并通过实验验证结果可行性[8-9]。陈长海等人通过分析冲击波和破片在空气中的运动规律,对破片式战斗部空中爆炸下冲击波和破片的耦合作用机制进行研究,考虑了壳体对冲击波强度的影响,建立了冲击波与破片耦合作用区间的理论计算模型,并与实验结果对比进行了可行性验证[10]。吴震等人进行了舰船板架在破片与冲击波共同作用下的毁伤效应实验。研究发现,光板的主要破坏模式包括花瓣弯曲破坏和拉伸断裂破坏,并对比分析了光板和加筋板在耦合载荷作用下的响应结果。这些研究结果对于理解和评估破片和冲击波共同作用下的目标毁伤效应具有重要意义[11]。
综上可知,目前对飞机毁伤效应研究对象主要包括飞机旋翼,机翼,等效靶板居多,材料主要为铝合金、钛合金以及钢材料居多。然而,不同结构形式的金属在联合毁伤下的毁伤效应区别较大,毁伤机理复杂多变,尚未进行充分研究。
本文通过LS-DYNA 仿真模拟软件进行了高精度高速破片和冲击波联合毁伤数值模型的建立与验证。结合FEM-SPH 算法补足了传统有限元算法在计算大变形、高应变率问题的缺陷。运用验证过的有限元模型,进行了不同速度球形破片和不同比距离冲击波两种毁伤元的联合毁伤模拟仿真,对飞机后机身结构在不同交会条件下的损伤特点进行分析,得出飞机结构的战伤机理,为飞机防护性设计提供参考,为部队抢修演练战伤预置提供基本输入。
1 数值模拟
1.1 FEM-SPH 自适应耦合算法
在本文所述的飞机典型结构战伤数值模拟采用了FEM-SPH 自适应法,能较为准确地对模拟打击后目标结构的损伤形貌、损伤机理等进行表征,同时反应出高速冲击下整个冲击流程和碎片云现象,并且保证了模型的计算效率,结合了传统FEM 与SPH 两种方法的优势。本文中的FEM-SPH 自适应耦合算法的初始模型采用了基于Lagrange 算法的六面体有限元单元,当结构所定义材料满足失效标准删除后,该方法将使用粒子代替删除的单元并继承原单元所有的节点属性。FEM-SPH 自适应耦合算法中提供的耦合算法需要在计算过程中结合粒子和元素。本模型整体结构采用六面体单元的建模,与传统的有限元法一样,材料特性、失效准则、边界条件和接触算法等参量可直接在单元上定义。此外,应在特定区域元素处定义相关关键字,可将计算过程中失效的单元删除并替换为SPH 粒子[12]。
1.2 有限元模型
模型从后机身部位等效,其由三个部件组成:蒙皮、筋条1、筋条2。其装配后示意图如图1所示,具体各部件尺寸如表1 所示。

图1 后机身等效模型Fig.1 Rear fuselage equivalent model

表1 后机身等效模型各组成部分Table 1 Components of the rear fuselage equivalent model
对于后机身模型,为了与局部细化相适应,共划分出有限元计算元件8 个,即将实体分成8部分,网格单元总数610272 个。单元全部为3D单元,局部加密部分单元三个方向尺寸均为0.5mm,未加密部分单元三个方向尺寸均为1.5mm。网格划分情况如图2 和表2 所示。
破片形状和尺寸参数如图3 和表3 所示。

图3 球形破片有限元模型Fig.3 Finite element model of spherical fragments

表3 球形破片有限元尺寸Table3 Finite element dimensions of spherical fragments
本文飞机典型结构件采用钛合金,使用了LS-DYNA 中15 号材料模型*MAT_JOHNSON_COOK,采用了cm-g-μs 为基本单位制,使用了*CONTACT_AUTOMATIC_SURFACE_TO_SUR FACE 自动面面接触关键字来设置部件之间的通用接触关系,使用*CONTACT_ERODING_SURFACE_TO_SURFACE 关键字来定义高速运动的破片对其他结构体的侵彻接触,采用LOAD_BLAST_ENHANCED 模拟冲击波输入,使用*SPC_SET 关键字在模型周围添加固接的边界条件如图4 所示。为了克服高速冲击后材料的大变形导致有限元网格计算不准,甚至过早出现单元负体积导致计算终止的问题,同时也为了更好地模拟实际情况下,高速冲击后在冲击位点和运动入射物附近产生的大量碎片云的物理现象,本仿真研究采用了 LS-DYNA 提供的*DEFINE_ADAPTIVE_ SOLID_TO_SPH 关键字,这一关键字的主要目的是创建SPH 粒子来对拉格朗日网格单元进行代替或补充,其会自适应地在拉格朗日固体部件或部件集合处生成SPH 粒子,当拉格朗日固体部件处某一单元失效时,激活当地的SPH 粒子。这一代替失效固体拉格朗日单元的SPH 粒子继承了失效固体单元的所有拉格朗日节点量和积分点量[13,14]。

图4 模型固接端面Fig.4 Model fixed end face
1.3 数值验证
如图5,表4 所示,菱形破片对模型进行侵彻的实验结果,使蒙皮和筋条出现破口,右上角筋条出现撕裂损伤,伴随花瓣状鼓起外翻,下方筋条出现不规则条状撕裂,与与本体出现大面积脱落分离现象,与实验结果相一致。图5 中破口尺寸约为1.35cm,与仿真结果为1.32cm 误差仅为 2.2%。破片侵彻结束,实验剩余速度为1932.2m/s,仿真结果为1983.9m/s,误差为2.35%。

图5 数值仿真验证对比图Fig.5 Comparison of numerical simulation verification

表4 球形破片有限元尺寸Table 4 Finite element dimensions of spherical fragments
侵彻过程大变形的网格转换为SPH 粒子代替单元继续进行计算,蒙皮上方SPH 粒子向溅起向四周飞散,侵彻结束大量粒子随着菱形破片一同继续向下运动,然后逐渐向周围扩散开来。
1.4 冲击波峰值超压
冲击波峰值超压是指冲击波阵面峰值压力与空气初始压力之差。TNT 球形装药在无限空气介质中爆炸时,冲击波峰值超压计算公式为[14]
式中,ω是战斗部等效的裸露TNT 装药的质量,单位是千克(kg);r是距爆炸中心的距离,单位是米(m);ΔPm是冲击波峰值超压,单位是兆帕(MPa)。无限空气介质爆炸是指炸药在无边界的空气中爆炸。式(1)是针对球形TNT 装药在无限空气介质中的爆炸情况,对其他形状种类的装药,通常进行等效[15]。
2 结果讨论与分析
2.1 不同比距离数值仿真
本系列采取4 种工况进行对比分析,控制爆炸距离为0.5m,通过改变爆炸当量来调整冲击波加载的比距离,研究不同比距离下模型出现的不同形貌变化,从而对冲击波对飞机后机身模型的毁伤机理进行分析研究。
2.1.1形貌分析
图6 为不同比距离下,在冲击波正压作用300us 时后机身截取模型的应力云图,为了更清楚显示模型的应力应变分布,将SPH 粒子和破片隐藏,随着爆炸当量的增大,比距离减小,模型呈现倒W 型的整体毁伤形貌,蒙皮与边界发生脱离,由于筋条的支撑,模型中心和两侧开始出现大面积塑性弯曲,当比距离继续减小,蒙皮开始出现大面积撕裂,无法维持原形貌继续实现其既定功能。
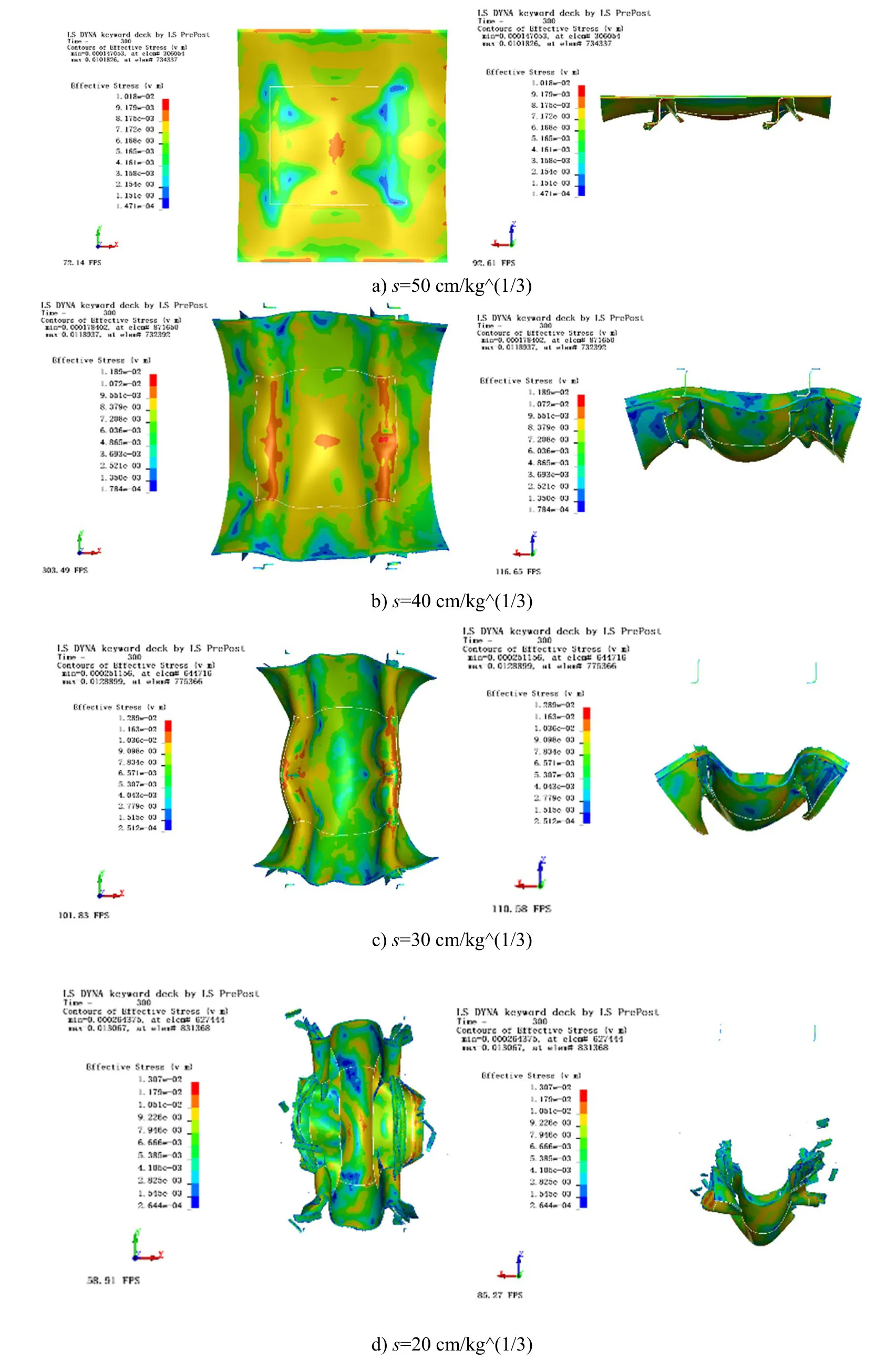
图6 不同比距离下毁伤形貌图Fig.6 Damage topography at different specific distances
2.1.2节点挠度变化
取模型节点17761,67909,762009,给他们编号为1,2,3 位置如图7,观察他们的随时间的挠度变化曲线。
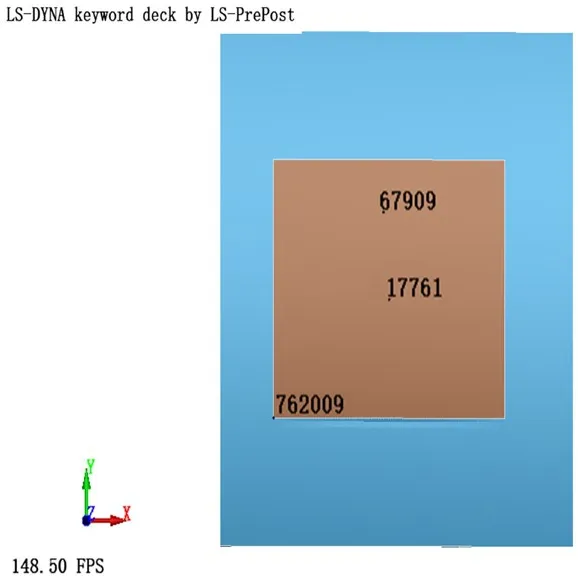
图7 节点在结构位置Fig.7 Node in the structure
从图8 中曲线可以看出,同一位置节点,在不同工况下,挠度随着比距离减小而增加。且在冲击刚加载时变化最快,后速度逐渐下降。在两根筋条中间区域,沿着筋条方向的点挠度接近,且因为筋条支撑作用,挠度变化从中心到两边递减。
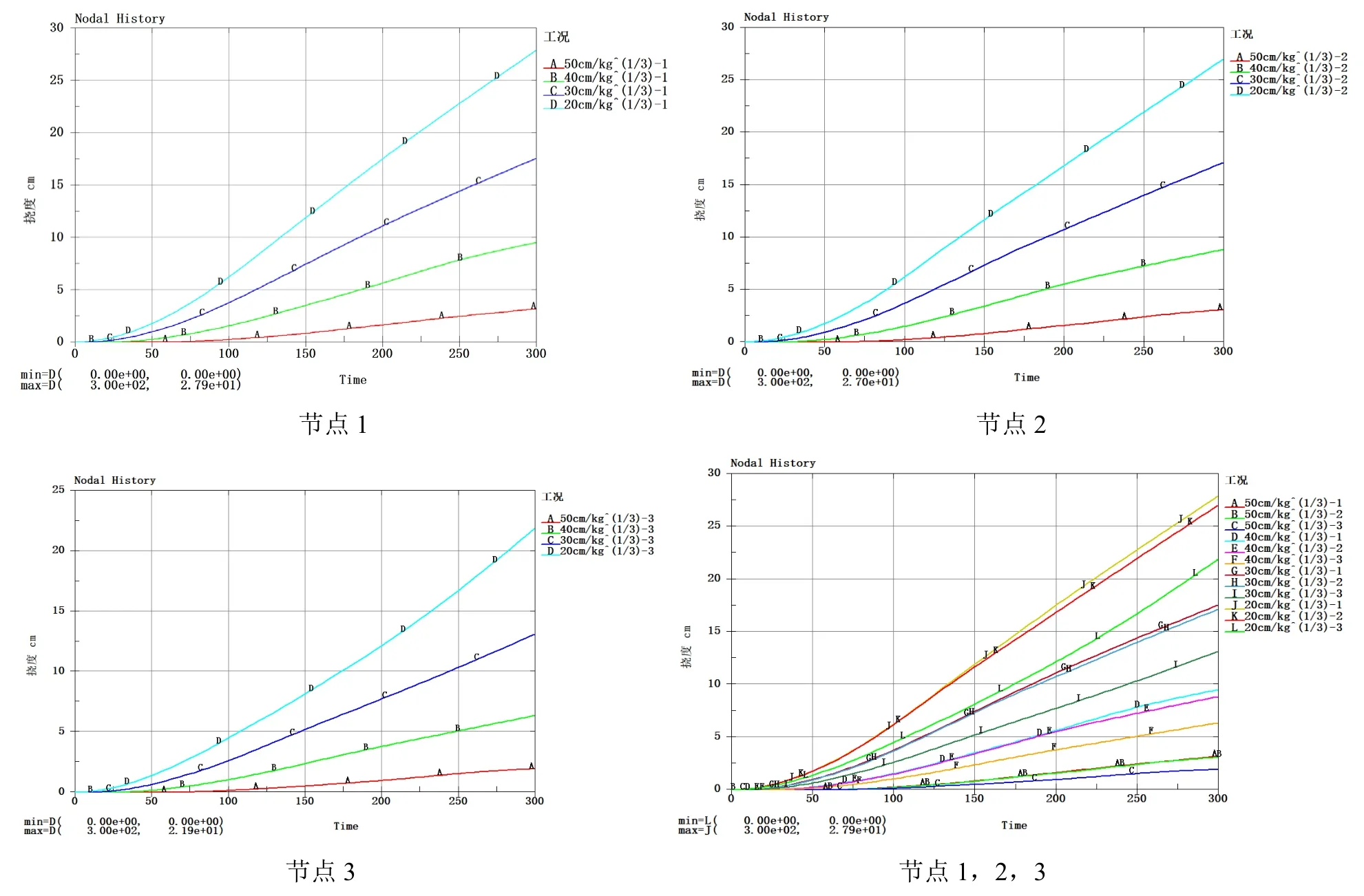
图8 各节点挠度随时间变化曲线Fig.8 Deflection curves of each node over time
2.2 冲击波-破片
本系列设定四种相似工况进行对照,杀伤元输入条件为冲击波作用点在蒙皮中心,爆炸当量设置为8kg,距离为0.5m,其改变量为球形破片速度从1800-2400m/s,变化梯度为200m/s 递增。冲击波从0us 开始加载,后在100us 破片以预先设定初速度启动[16]。
2.2.1形貌分析
由于四种工况下毁伤形貌重复性较大,故取破片速度为2400 m/s 的工况进行详细分析。如图9 所示,在冲击波加载下,在100us,模型上蒙皮板出现大面积塑性变形,筋条由原来的z 字型,在冲击波载荷加载下被下压接近一字型。蒙皮表面未出现破口或撕裂状损伤表现。在100us 将破片施加初速度,破片对变形后的模型进行侵彻,因为本仿真采用有限元与SPH 粒子耦合的算法,可看到侵彻过程有大量单元转换成SPH 粒子发生飞散,筋条处的破片由于模型冲击波预先加载产生的变形,粒子分布较为分散。蒙皮中心处破片,粒子在上面向四周进行飞溅,呈现圆形分布,下面近似呈一条直线,随着破片侵彻方向向四周飞散。侵彻结束后,中间的破口呈现圆形剪切破口,尺寸与球形破片接近,筋条处表现为大面积剪切破口损伤,边缘伴随撕裂和单元脱落现象。图10 是整体毁伤形貌图。
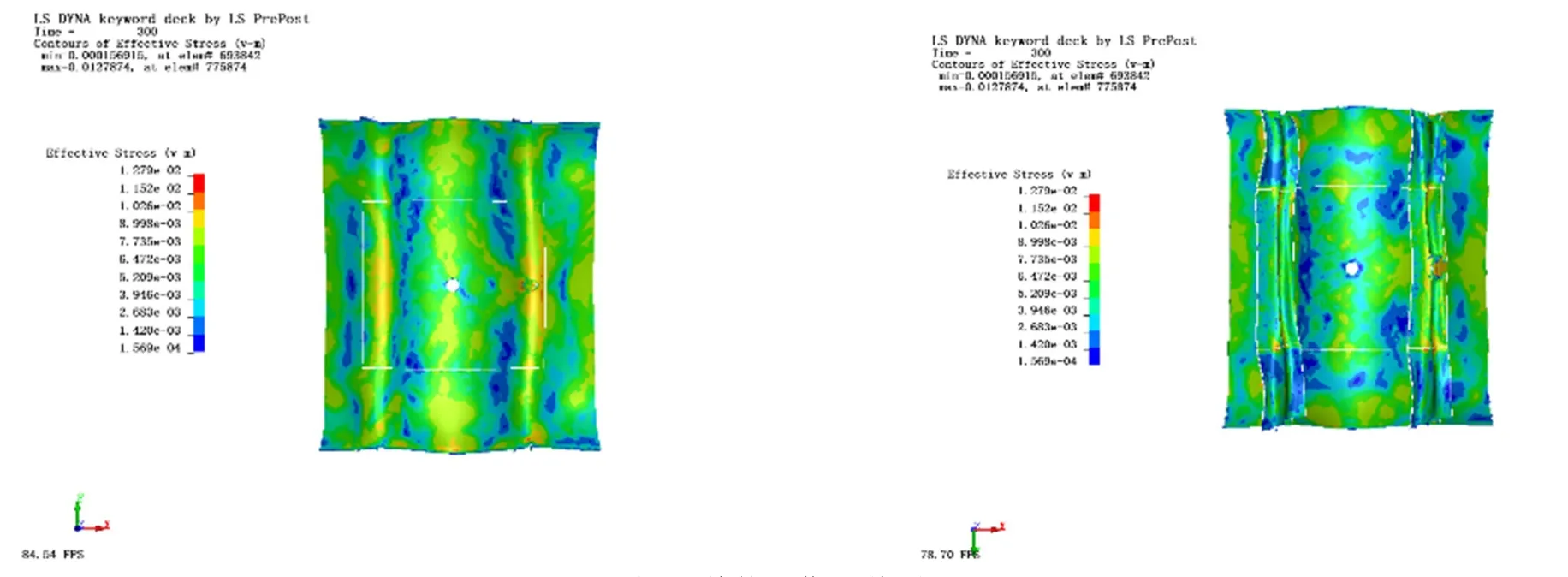
图10 整体毁伤形貌图Fig.10 Topography of the overall damage
2.2.2球形破片剩余速度
从图11 和表5 中可以看出,破片在100us被赋予2400m/s 的初速度,由于设置输出间隔为3us,取样点在99us 和102us,所以拟合曲线会有一个加速度上升趋势。
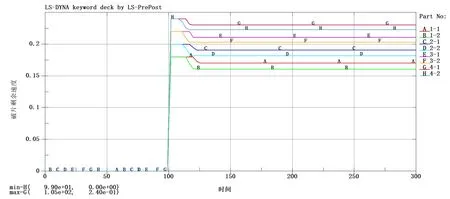
图11 破片剩余速度曲线Fig.11 residual velocity curve of fragments
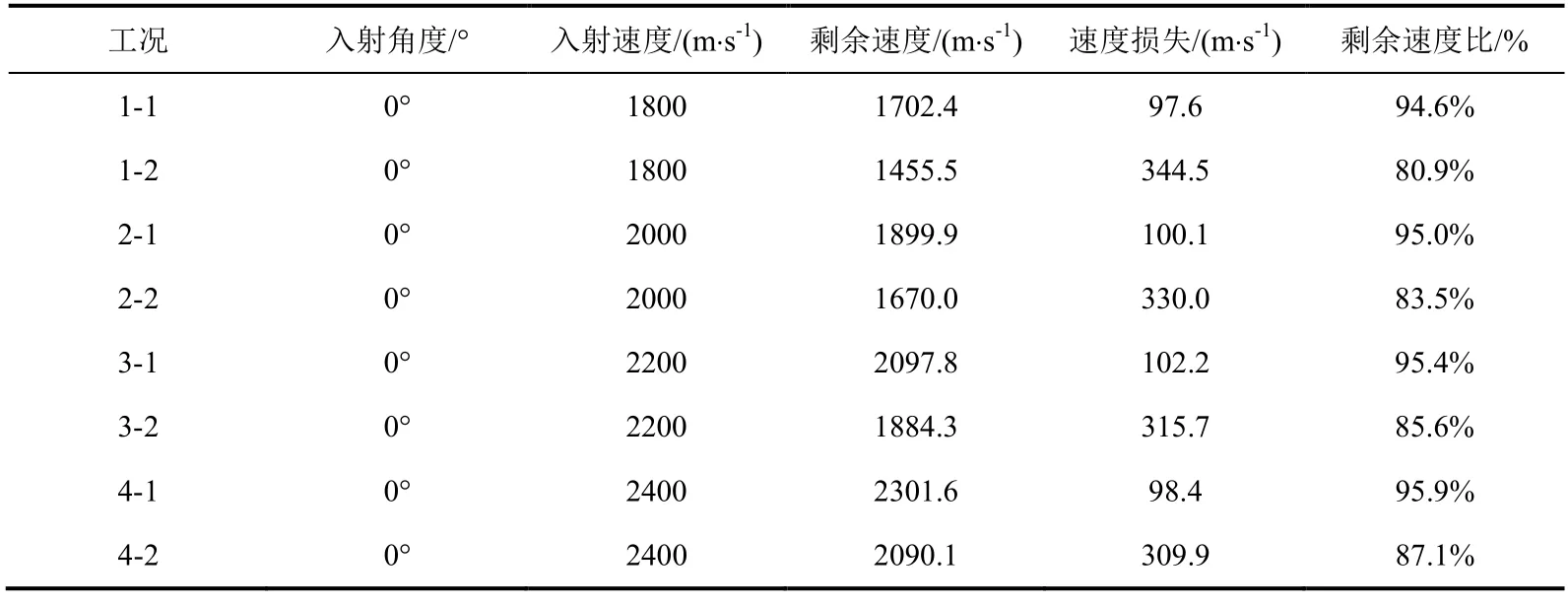
表5 破片速度参数Table 5 Fragmentation velocity parameters
在侵彻蒙皮中心过程中,速度曲线从开始侵彻到侵彻结束过程中加速度逐渐下降,斜率曲线呈现一个由陡变缓的趋势。由于破片初速度较高,所以四种工况侵彻过程时间几乎相同,虽然2400m/s 相较于1800m/s 侵彻时间略短,但其对模型侵彻产生较大的阻力,所以四种工况下产生的冲量大小接近,且四种速度工况下球形破片剩余质量几乎相同,这也就导致破片的速度减小量都在100m/s 附近浮动。随着初速度增大,剩余速度的百分比略有提升。
在侵彻蒙皮和下方筋条过程中,由于冲击波的预先加载,导致筋条从Z 字型发生塑性变形趋近于一字型,蒙皮在筋条上方的两侧也呈现出轻微的V 字型弯曲变形,这直接导致侵彻情况变的复杂多变,在某一时刻可能由于变形后模型之间产生的缝隙使速度发生抖动,故不对侵彻过程中的速度变化进行过多研究。最终的速度损失随着初始速度增大出现略微下降趋势,剩余速度的百分比逐渐上升。
2.2.3剩余质量对比
如图12和表6所示,在侵彻蒙皮中心过程中,破片的质量损失随着初速度增大出现上升趋势,但由于蒙皮厚度较薄,所以破片损失质量不多,四种工况下剩余质量都接近90%。而在侵彻蒙皮和下方筋条过程中,由于筋条也在侵彻路径中,导致质量损失增加,剩余质量从90%左右下降至50%左右,变化趋势也与之前一致,随着初速度增加,质量损失出现轻微上升。
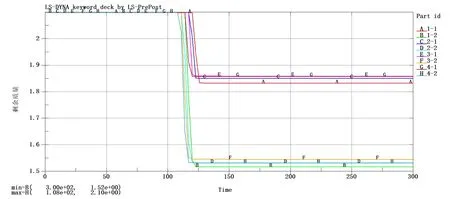
图12 破片剩余质量曲线Fig.12 Residual mass curve of fragments

表6 破片质量参数Table 6 Fragment quality parameters
2.3 破片-冲击波
本系列设定四种相似工况进行对照,杀伤元输入条件为,冲击波作用点在蒙皮中心,爆炸当量设置为8kg,距离为0.5m,其变量为球形破片速度从1800-2400m/s,变化梯度为200m/s 递增。破片从0us 开始加载,后在100us 冲击波开始加载。这样可以与先前四种工况形成对比,通过比对分析冲击波和破片先后加载对加筋板毁伤形貌影响,为飞机战伤研究提供参考。
2.3.1形貌分析
选取破片速度为2400 m/s 进行过程详细分析,图13 为球形破片在各个时刻对后机身模型的侵彻过程以及对应的破口毁伤形貌。初始时刻,两球分别位于蒙皮中心和筋条上方,T=12us,位于蒙皮中心上的球穿过模型,完成侵彻。而在筋条上方的球此时正与筋条接触发生侵彻,可以看到蒙皮处出现球形破口,筋条处沿着侵彻方向出现条形破口,且伴随撕裂。部分侵彻产生的破片发生脱落或者飞散与筋条发生二次侵彻。蒙皮上方粒子云飞散情况基本保持一致。T=24us 时,两个破片侵彻都已经结束,可以看到筋条新出现一个环状球形破口,但在侵彻路线上的筋条还有部分未出现单元失效,且未发生撕裂或剪切破坏,这是由于小球在侵彻过程中被筋条割裂成两半,一半从右侧打穿筋条下半部分,另一半与模型分离继续向初速度方向运动。可以看出破片穿过模型时,只对附近区域产生较为显著影响,会有大面积剪切失效,伴随条状撕裂,还有一圈塑性变形。而对离侵彻部位较远的区域不会产生影响。
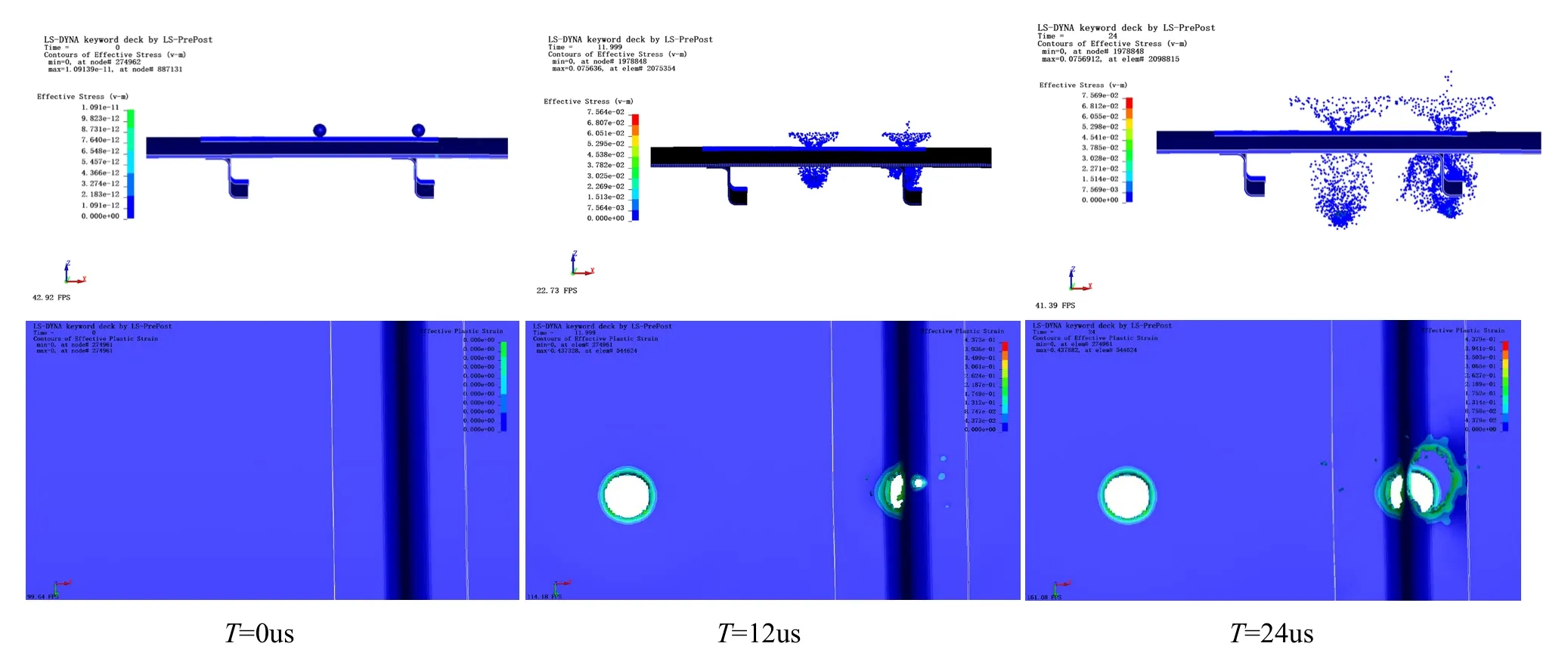
图13 不同时刻侵彻粒子云分布以及破口毁伤形貌对比Fig.13 Comparison of the distribution of penetrating particle clouds and the morphology of breach damage at different times
从图14 中可以看出,筋条下方的环形破口在冲击波的加载下发生断裂,两侧出现花瓣状外翻现象,后与模型发生撕裂分离,且破口周围出现裂纹拓展现象。蒙皮出现大面积的塑性变形,出现Z 向挠度变化,导致蒙皮下方与筋条发生贴合现象,阻碍球形破口裂纹拓展现象的发生,故破口周围只是出现轻微裂纹拓展。

图14 冲击波加载后毁伤形貌Fig.14 Damage to the topography of the shock wave after loading
蒙皮中心破口在冲击波正压持续作用下两边出现裂纹拓展现象,出现针头状裂纹,且由于右侧发生侵彻,筋条和蒙皮挠度变化较大,故右边裂纹长度明显长于左边,若提高爆炸当量,不难预测裂纹会进一步延伸直至联通两处破口。
2.3.2球形破片剩余速度
从图15 和表7 可以看出,在侵彻蒙皮中心过程中,速度损失都在200m/s 附近浮动,这与上一系列先加载冲击波后加载破片的工况分析所得出的结论保持一致。但由于冲击波对模型造成冲击破坏,导致蒙皮和筋条出现大面积塑性变形,导致蒙皮强度下降,本系列侵彻速度相较于上一系列损失显著增加,剩余速度百分比下降。

图15 破片剩余速度曲线Fig.15 Residual velocity curve of fragments
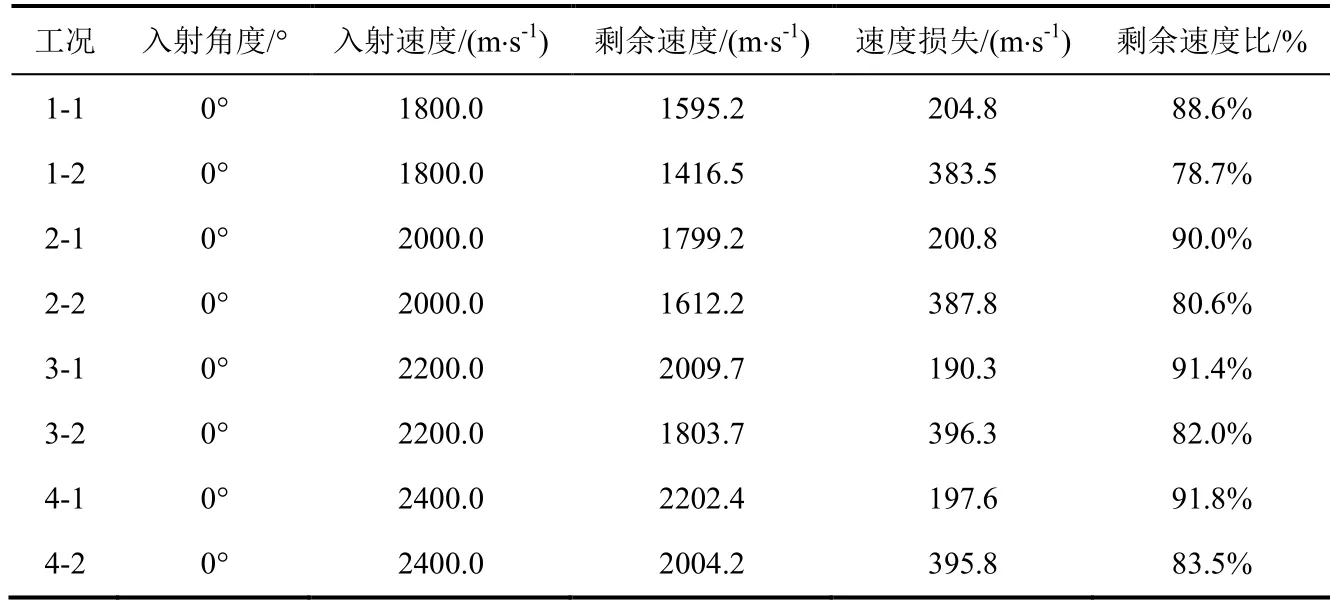
表7 破片剩余速度参数Table 7 Residual velocity parameters of fragments
在侵彻蒙皮和下方筋条过程中,速度损失在390m/s 附近浮动,与之前得出结论保持一致。且相较于上一系列,随模型未在冲击波的预先加载下出现大面积塑性变形以及强度下降的情况,但由于侵彻过程中球形破片被割裂成两半,导致有一部分小球未发生侵彻而出现速度损失,所以最终速度损失相较于前一系列只出现轻微增加,且随着初速度提高呈现上升趋势,与之前有所不同。
2.3.3剩余质量对比
从图16 和表8 可以看出,在侵彻蒙皮中心过程中,球形破片质量损失在0.5g 左右,剩余质量约为75%,随着初速度增加无明显变化趋势。相较于上一系列,由于冲击波在破片侵彻之后到达,模型未出现大面积塑性变形和强度下降,导致质量损失提升了0.25g -0.35g。
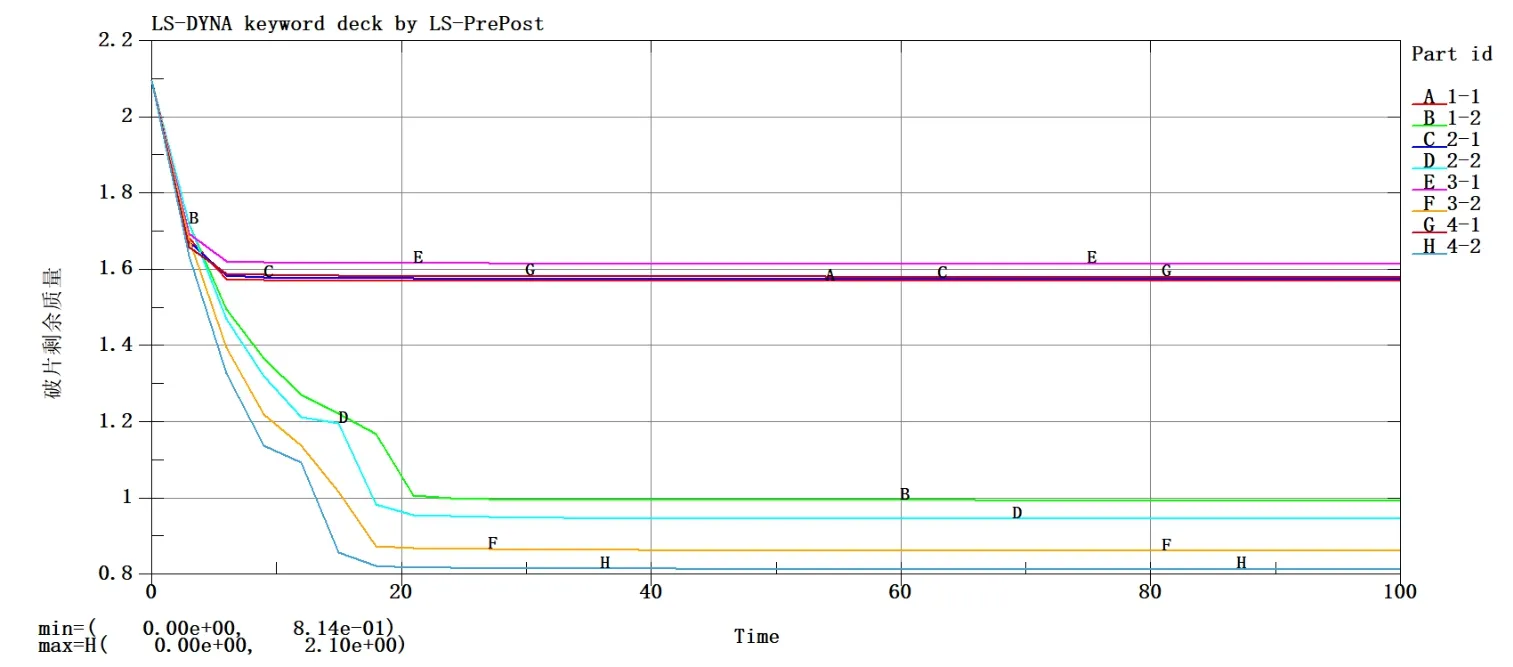
图16 破片剩余质量曲线Fig.16 Residual mass curve of fragments
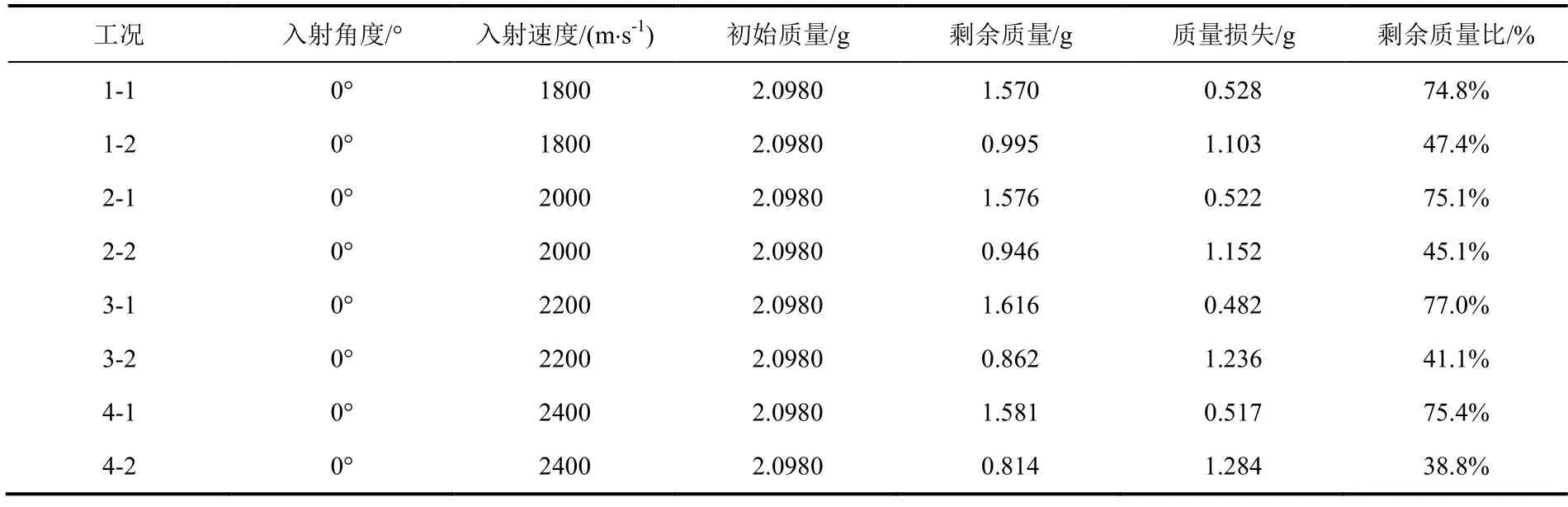
表8 破片剩余质量参数Table 8 Residual mass parameters of fragments
在侵彻蒙皮和下方筋条过程中,破片质量损失在1.2g 左右,随着初速度的增大,质量损失出现轻微上升趋势,在初速度达到2400m/s 时,破片剩余质量仅为38.8%。相较于冲击波预先加载的情况,破片质量损失上浮约10%,这是由于冲击波的预先加载导致筋条趋于一字型,这使破片与模型接触时间减少,导致侵彻过程质量损失减少。可以看出,冲击波对于模型强度的破坏效果是比较明显的。
3 结论
本文针对飞机后机身部位截取的等效模型进行破片和冲击波联合毁伤研究,跟据飞机在战斗过程中可能受到的武器威胁,利用LS-DYNA 构建了毁伤仿真模型,通过实验对模型进行了数值可行性验证,对使用钛合金材料的等效模型进行单独冲击波毁伤、先冲击波后破片联合毁伤、先破片后冲击波联合毁伤仿真计算,得到了不同系列工况下的毁伤机理,主要结论如下
1)冲击波单独毁伤形貌分析表明,在冲击波的加载下,由于筋条的支撑作用,蒙皮的中心和两侧出现大面积塑性变形,呈现W 型毁伤形貌,当继续减小爆炸比距离,蒙皮开始出现大面积撕裂,大量单元失效,无法维持原貌实现原有功能。
2)经过把不同初速度破片进行对比表明,球形破片侵彻钛合金模型破口主要变现为剪切变形,且伴随单元撕裂,当初速度较高时,破片初速度对破片速度损失量几乎没有影响。破片在侵彻筋条过程中质量损失较大,甚至被割裂成两半,飞散的破片碎片会造成二次侵彻。
3)在冲击波的预先加载下,模型出现大范围塑性变形,结构强度下降,后加入破片侵彻会比原来更易打穿模型,且损失的质量也会减少。当破片先加载的情况下,后加入的冲击波会对侵彻产生的破口进行二次毁伤,出现边缘撕裂和裂纹拓展的现象。
