采用m函数定义Sturm Liouville问题的广义特征多项式

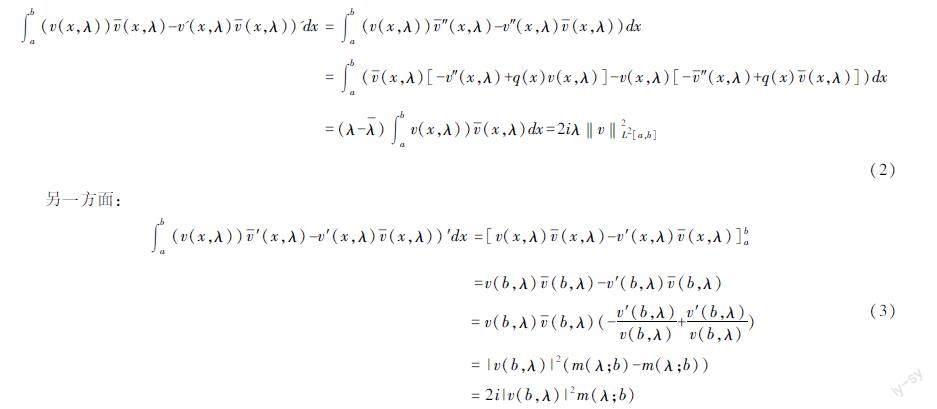
摘要：分析SturmLiouville问题的m函数对谱参数与端点的导数，以此推出谱参数分段单调性。通过m函数定义SturmLiouville问题广义特征多项式，从而得出SturmLiouville问题谱对参数、边界的导数简短证明。

关键词：m函数；SturmLiouville问题；广义特征多项式

充分考虑SturmLiouville方程，在1910年H.Weyl将SturmLiouville方程划分为极限圆型与极限点型，极限圆型值指的是任意λ∈C/R，SturmLiouville方程所有解都为平方可积；极限点型指的是对于任意λ∈C/R，方程有且只有一个解为平方可积。有研究人员在此基础上设置了有效处理工具，也就是TitchmarshWeylm（λ）理论，利用m（λ）函数性质对奇异SturmLiouville问题谱问题进行讨论，对于m（λ）函数具有重大研究意义。

在t=0点附加边值条件：

y（0）sina-y’（0）cosa=0

-π/2<a≤π/2

以此构成SturmLiouville边值问题，分析不同函数中的m（λ）函数比较定理。公式分别为Pro（q）和（1）q，以下给出结论：

充分考虑a=π/2时候的两个奇异边值问题Pro=（q1），Pro（q2），为右定且为极限点型，并且使所对应m（λ）函数作为m1（λ）与m2（λ）。-∞<λ0<λ1<…<λn<…为m1（λ）的极点；另外，-∞<u0<u1<…<un<…为m2（λ）的极点。

如果q1（t）≤q2（t），a.e.t∈（a，∞）

其次，（λk-1，λk）⌒（uk-1，uk）=（ξk-1，ξk）≠￠的时候，在k=0的时候，λ-1，u-1，ξ-1指的是-∞，那么（ξk-1，ξk）为必有的：

m1（λ）≥m2（λ）

1有限谱问题分析

微分算子指的是线性算子中使用比较广泛的算法，也就是描述固体热传导问题的数学模型从而产生的SturmLiouville问题研究，因为实际使用背景，促进了微分算子谱理论的发展。经典SturmLiouville问题被广泛使用，研究领域从正则问题转变到奇异问题。一般来说，经典SturmLiouville问题或者高阶微分方程解和解的拟导数在定义区间中为绝对连续函数，但是此条件有很多数学物理或者工程技术领域中的问题无法满足，比如内部存在不连续性问题。此问题指的是微分方程解或者解的拟导数在微分算子定义区间中的发生间断，为了解决此问题，要在不连续点处附加条件，也就是转移条件。

简单来说，SturmLiouville谱问题指的是通过谱数据得出算法的形式，此问题在数学、电子、物理和其他自然科学分支中使用。逆谱问题对于解决数学物理中非线性发展方程尤为重要，针对一般经典SturmLiouville问题来说，特征值个数是无穷尽的。但是有研究人员提出，在方程中系数满足部分条件的时候，SturmLiouville问题存在有限个特征值。此类有限谱问题研究和矩阵特征值问题具有密切的关系，矩阵特征值问题为代数理论或者矩阵理论主要研究方向，此问题被广泛应用到力学、光学、结构设计等方面。另外，部分特殊矩阵问题的使用前景更加广泛，比如Jacobi矩阵在生物学中的使用背景就是物种迁移优化问题。针对矩阵特征值逆向问题来说，相关人员给出了逆矩阵特征值的问题起源与结论。无穷维矩阵特征值问题被广泛应用到生物统计学中，还是代数问题中的主要研究方向，包括动力系统红的熵、流、稳定性等。

以此认为，不连续SturmLiouville问题逆谱问题就是：针对两组交错实数，存在一类不连续SturmLiouville问题，使得到的给定两组实数为SturmLiouville方程在不同两组边界条件中的特征值，使用的方法也就是Atinson型SturmLiouville问题和矩阵特征值问题等价性。

2逆结点问题

通过物理学角度分析，逆结点问题指的是在本征摆动过程中的一束光振幅为零的位置，对此束光的密度进行确定。逆结点利用特征函数节点对算子重构，一般特征函数零点可测，特征方程标准常数无法测量，所以可以通过结点作为数据重构边界条件和势函数。

McLaughlin属于充分考虑一维Schrodinger方程逆结点的数学家，其证明只需要特征函数节点稠密子集就能够对SturmLiouville问题进行确定的势函数，从而得出唯一性定理，对两个SturmLiouville问题进行考虑：

y（x）+［λ-qi（x）］y（x）=0，i=1，2

边界条件为：

y（0）=y（1）=0

此问题为势函数qi的第n个特征函数结节点，假设对于每个n能够寻找j∈{1，2，…，n-1}，结节在公共集［0，1］中为稠密的，那么q1=q2，a.e.［0，1］。之后，Hald等人用同樣的方法使唯一性定理推广到一般边界条件中，并且创建重构算法。Yang使用McLaughlin方法对唯一性结论进行证明，并且得出逆结点问题的显式解。

在20世纪50年代后，人们发现在很多工程领域中的SturmLiouville问题谱参数会出现在方程和边界条件中。针对边界条件带参数SturmLiouville问题是通过热力学、波动力学等偏微分方程中利用分离变量得出的，针对具备参数多项式边界条件SturmLiouville问题，充分考虑：

-y（x）+q（x）y（x）=λy（x），x∈［0，1］

公式中q（x）为实值连续函数，节点稠密子集可唯一确定边界条件参数和势函数，但是并没有给出利用节点重构。Freiling等人使参数边界条件在任意实系数多项式，利用离散谱数据、Weyl函数重构算子，并且得出重构算法。另外，还得出带参数边界条件SturmLiouvlle问题特征函数渐进估计式。

以上述结论表示，假如在参数边界条件中的整个区间节点稠密子集为唯一确定势函数与边界条件。因为Yang所证明的分离型边界条件下部分区间中的结点信息对算子确定。

3m函数

假设v（x，λ）方程能够满足初始条件y（a）=1，y1（a）=h的解，那么通过常微分方程对于参数具备连续依赖性。定义xb处的WrylTitchmarshm函数：

m（λ；b）：=－v′（b，λ）v（b，λ）（1）

其中m（λ；b）为半纯函数。

区间［a，b］为边条件（1.2）与y（b）=0构成的自伴SturmLiouville问题谱为{λDn|n=0，1，…}，其中λDn为实数，并且为v（b，λ）的全部零点，也就是m（λ；b）的全部极点。

对于固定b，m（λ；b）为Herglotz的函数，指的是在上半复平面的半纯函数：

∫ba（v（x，λ））v-（x，λ）－v'（x，λ）v-（x，λ））'dx=∫ba（v（x，λ））v-″（x，λ）－v″（x，λ）v-（x，λ））dx

=∫ba（v-（x，λ）［－v″（x，λ）+q（x）v（x，λ）］－v（x，λ）［－v-″（x，λ）+q（x）v-（x，λ）］）dx

=（λ－λ-）∫bav（x，λ））v-（x，λ）dx=2iλ‖v‖2L2［a，b］（2）

另一方面：

∫ba（v（x，λ））v-′（x，λ）－v′（x，λ）v-（x，λ））′dx=［v（x，λ）v-（x，λ）-v′（x，λ）v-（x，λ）］ba

=v（b，λ）v-（b，λ）－v′（b，λ）v-（b，λ）

=v（b，λ）v-（b，λ）（－v′（b，λ）v（b，λ）+v′（b，λ）v（b，λ））

=|v（b，λ）|2（m（λ；b）－m（λ；b））

=2i|v（b，λ）|2m（λ；b）（3）

通過以上公式得到：

m（λ；b）λ=‖v‖2L2［a，b］|v（b，λ）|2>0

因为Herglotz函数会被极点，留数和沿虚线轴趋于无穷时渐进性唯一确定，在对逆谱问题研究过程中为主要性质。

4主要结果

定理1：如果常数－ba∈（λDn，λDn+1），公式中的λDn与λDn+1指的是右端取Dirichlet边条件的SL问题某相邻特征值，记作为λD-1=—∞，那么：

λ0<λD0<λ1<λD1<…<λn-1<λDn-1<λn<λ-ba<λn+1<λDn<λn+2<…

如果常数-ba=λDn，也就是aλDn+b=0，那么：

λ0<λD0<λ1<λD1<…<λDn-1<λn<λ-ba=λn+1=λDn<λn+2<…

证明：因为函数m（λ）在区间（λDk+1，λDk）（k=0，1，…）中连续，所以F（λ）在区间（λDk+1，λDk）（k=0，1，…，n-1，n+1，…）和（λDk+1，λDk）中也连续。通过a>0得知，－1aλ+b在（-∞，-ba）和（-ba，+∞）中单调递增：

limλ→－ba－0－1aλ+b=+

（4）

另外，F（λ）区间（λDk+1，λDk）（k=0，1，…，n-1，n+1，…）和（λDk+1，λDk）中单调递增，并且：

limλ→λDn+0F（λ）=－

（5）

所以此连续函数介值定理得到F（λ）在区间（λDk+1，λDk）（k=0，1，…，n-1，n+1，…）中有且只有一个零点，通过上述方程生成SL问题特征值。

如果-ba=λDn，那么1aλDn+b=

，m（λDn）=∞，已知-ba=λDn也是SL问题特征值，得证。

定理2：在区间［a，b］中充分考虑m（λ，b）函数，也就是y（t，λ，b）=y1（t，λ）+m（λ，b）y2（t，λ）为方程满足a点边界条件m（λ，b）y（a）-y′（a）=0，在b点满足边界条件y（b）=0的解，也就是：

λn（b）对固定n相关b的严格单减；

在λ∈（-∞，λ0（b））的时候，y（t，λ，b）在（a，b）中设置零点，在λ∈（-∞，λ0（b））的时候，y（t，λ，b）在（a，b）中的零点为k。

证明：先证明第一个部分：通过{λn（b）}定义得到y2（b，λn（b））=0，并且y2（t，λ）在a点能够满足y（a）=0，y’（a）=1。通过Prufer变换得知，y2（t，λn（b））处于a点辐角为0，在b点辐角为（n+1）π。假设b2>b1，因为y2（t，λn（b1））=0，y2（t，λn（b2））=0，所以（b1，λn（b1））=（n+1）π。

定理3：充分考虑a=π/2奇异的边值问题Pro（q1），假设m1（λ）的极点可排列：

-∞<λ0<λ1<…<λn

另外，u（t，λ）=θ（t，λ）+m1（λ）ψ1（t，λ）为满足方程初始条件的唯一平方可积解，那么在λ∈（-∞，λ0）的时候，u（t，λ）在（a，∞）中没有零点。在λ∈（λk-1，λk）的时候，u（t，λ）在（a，∞）中零点有k个。

证明：在不同边界条件中，相同方程特征值相互交错，关系式为：

m（λ，a）=m（λ，β）+tan（β－a）1－tan（β－a）m（λ，β）（6）

通过此公式得到β=π/2，得出：

m（λ，a）=m（λ）+cota1－cotam（λ）（7）

在-β/2<a≤β/2，a≠π/2的時候，m1（λ）=tana的λ值就是Pro（q1）特征值。在a=π/2的时候，m1（λ）函数处于（-∞，λ0）还是从-∞递增得到的。对任意所取的常数T，-∞<T<∞，在m1（λ）函数每个区间都有1个λ，m1（λ）=T。推出λk（0≤k≤n）为特征值，存在k个零点，之后通过T任意性得证。

定理3：对于固定h和实数a>0与b，{λn}+∞n=0与{λDn}+∞n=0为唯一确定q（x）

证明：通过定理1证明，得证。

参考文献：

［1］傅守忠，王忠.边条件含谱参数有理式的SturmLiouville问题的谱不等式［J］.肇庆学院学报，2019，40（02）：710+22.

［2］刘肖云，史国良，闫军.具有转移条件的向量型SturmLiouville问题的特征值重数及Ambarzumyan定理［J］.应用数学学报，2020（1）：3348.

［3］朱军伟，顾丽娜.具有转移条件且边界条件中含有多项式谱参数的SturmLiouville问题的有限谱［J］.兰州文理学院学报（自然科学版），2019，33（06）：711+57.

［4］刘娜娜，敖继军.时标上具有分布势函数的SturmLiouville问题的矩阵表示［J］.应用数学，2019，32（03）：515524.

［5］高承华，吕莉.边界条件含有特征参数的二阶离散SturmLiouville问题的谱［J］.西北师范大学学报（自然科学版），2019，55（06）：15.

［6］马慧敏，杨树生，庞晶.SturmLiouville问题的特征值特征［J］.内蒙古工业大学学报（自然科学版），2020，39（02）：8186.

［7］赵迎春，孙炯，姚斯琴，等.具有无穷多个不连续点SturmLiouville算子的Friedrichs扩张［J］.数学的实践与认识，2020，50（06）：229236.

［8］竺晓霖，翟成波.一类二阶微分方程SturmLiouville边值问题正解的局部存在性与唯一性［J］.山东大学学报（理学版），2019，54（10）：9196+108.

作者简介：陆骞（1987—），男，汉族，江苏无锡人，本科，讲师，研究方向：高等数学、高职数学教育。