基于Winograd算法的高效神经网络加速器及FPGA实现

王帅帅, 陈 强, 郭剑博, 肖 昊

(合肥工业大学 微电子学院,安徽 合肥 230601)

卷积神经网络(convolutional neural networks,CNN)具有良好的图像特征提取功能,广泛应用于图像分类[1]、船舶识别检测[2]和井下视觉识别[3]。 传统卷积运算包含大量乘累加计算,使神经网络模型部署至资源有限的现场可编程逻辑门阵列(field programmable gate array,FPGA)设备存在困难。 因此减少卷积计算中乘法次数和降低乘法计算位宽,将CNN高效部署至FPGA成为近年研究热点。

在算法层面,Winograd[4]和快速傅里叶变换(fast Fourier transform,FFT)卷积算法[5]可减少卷积乘法次数,广泛应用于CNN加速器设计。 目前网络模型卷积朝卷积核尺寸小、数量多的方向发展,相比FFT算法,Winograd算法在缩减小尺寸卷积乘法次数方面更加高效[6]。 Winograd算法通过矩阵变换将卷积数据映射至Winograd域,使用加减法代替乘法,其点乘步骤为2个二维矩阵点乘,可高效映射至FPGA加速器的二维运算阵列,进行并行化处理,提升运算速度。

文献[4]首次将Winograd算法应用于CNN模型,经实验得小尺寸Winograd卷积算子的误差更低,但文献[4]的设计仅适用于步长1的卷积类型;文献[7]设计适配Winograd算法和传统卷积算法的数据流,提出统一架构进行FPGA实现,扩展加速器适用范围,但转置步骤需线下运算,转置后数据需进行片上存储,导致FPGA片内存储器资源占用率高达90%;为扩展加速器适用范围的同时减少片上存储资源占用,文献[6,8]使用卷积分解方法,使Winograd算法适用于不同类型卷积,且设计线上转置模块,减少片上卷积核存储量。

文献[9]设计统一计算单元,处理不同类型卷积并使用数据复用策略减少数据搬运次数;文献[10]提出多模式可重构计算单元,提高计算资源利用率;文献[11]将Winograd算法应用于航空目标检测,进一步扩展算法的应用领域。 但上述设计存在量化后定点数据位宽与数字信号处理单元(digital signal processing,DSP)位宽失配的问题,使得FPGA的DSP利用率降低。

针对高效Winograd卷积加速器设计,为降低片上存储资源占用率,本文采用线上转置模块,数据转置后输入运算单元处理,实现输入数据复用且减少内存占用。

针对数据位宽失配问题,本文利用部分积切割方法,运算电路由DSP与查找表(look-up table,LUT)构成,缓解数据位宽失配,提高架构运算单元利用率。

1 CNN优化算法

1.1 CNN量化方法

低比特数据量化方法[10-14]将神经网络模型浮点数转为定点数,减少模型参数存储量。 本文使用TensorFlow Lite[12]量化方法将神经网络推断过程浮点数运算转为定点整数运算,并保证量化前后两数值的相关性。 此方法为嵌入式设备和FPGA高效部署神经网络提供便利。

CNN量化基本思路是将卷积浮点数运算转为定点整数运算。 卷积运算中定点整数q与浮点数r的仿射变换关系为:

r=S(q-Z)

(1)

其中,S、Z为统计得出的常量。S的计算公式为:

S=(rmax-rmin)/(qmax-qmin)

(2)

正值参数S由模型训练过程浮点数范围与量化后定点数范围比值得出,代表数值量化前后的比例,也称比例因子。Z的计算公式为:

Z=qmax-(rmax/S)

(3)

若Z为定点小数,则四舍五入转为定点整数。Z为浮点数零值对应量化后数值,也称零点。 CNN模型每个激活层对应一组量化参数,每个卷积核输出通道对应一组量化参数。

确定浮点数与定点数量化参数后,将卷积运算过程中运算步骤转为定点数运算。 浮点数卷积运算为:

(4)

其中:r1为卷积核元素;r2为输入特征图元素;r3为卷积输出特征图。 将浮点数利用TensorFlow Lite量化方法,仿射变换为定点整数,即

(5)

M=S1S2/S3

(6)

由式(6)可得,除M外其余为定点整数。 将M统一为式(7),使CNN推理过程为整数运算,即

M=2- nM0

(7)

其中,n为量化后定点整数位宽。 硬件实现时,式(5)中定点小数由左移n位以及与定点整数M0相乘2个步骤运算。

CNN模型训练结束后,统计得出卷积激活层和卷积核浮点数值范围。 量化参数线下计算,神经网络部署过程中量化参数由存储器存储。 CNN推断过程为定点整数运算,简化CNN模型卷积计算过程,利于嵌入式和FPGA设备部署工作。

TensorFlow Lite[12]方法量化后模型识别准确率符合网络模型精度要求,见表1所列,将VGG16、MobileNetV1、MobileNetV2网络模型量化[15]为8 bit定点整数后,模型精度仅下降3%。

1.2 Winograd算法基本原理

CNN应用Winograd算法中二维卷积算子,二维算子由一维算子嵌套得出[4]。 本文采用二维Winograd卷积算子,即

U=GFGT
V=BTIinB
Oout=AT[U⊙V]A

(8)

其中:F、Iin分别为神经网络卷积核与输入特征图;B、A、G分别为Winograd算法输入转置矩阵、输出转置矩阵、卷积核转置矩阵。 输出特征矩阵由中间结果矩阵U、V点乘并转置得出。

转置过程会产生误差,本文选择转置矩阵由0、1、-1、1/2、-1/2构成的算子,文献[4]实验表明此类算子误差数量级在10-5内,符合神经网络识别精度要求。 本文选取3×3卷积核、4×4输入块及2×2输出规模的Winograd卷积算子适配VGG16网络模型,记为F(2×2,3×3),其转置矩阵为:

(9)

F(2×2,3×3)卷积算子可用移位和加法操作实现,简化硬件实现复杂度。 CNN输入特征图是大规模特征矩阵,Winograd卷积算子无法直接匹配运算。 因此采用切片方式[7,16]将输入特征图(input feature map,IFMAP)划分为适配Winograd卷积算子的矩阵划块,最终将部分结果组合为输出特征图(output feature map,OFMAP),此结果与传统卷积输出等价。 卷积算子数据流如图1所示。

图1 Winograd卷积算子数据流

1) 本文采用F(2×2,3×3)卷积算子,输入划块大小为4×4。 VGG16模型卷积步长为1且卷积核尺寸为3×3,3×3卷积窗口在4×4输入划块进行2次水平滑动和2次垂直滑动,F(2×2,3×3)卷积算子每次输出4个传统卷积等价结果。 卷积核滑动步长为1,2个输入划块间存在重叠部分,重叠长度为卷积核长度与滑动步长差值,本文设计为2。 按上述规则取输入块,先横向提取首个输入通道IC,再纵向提取。 划块占满总宽度W和高度H,第1个输入通道划块提取完成,其余通道按相同规则划块。

2) 单通道卷积核K尺寸为3×3,卷积核通道总量与对应特征图输入通道数相等,卷积核个数与输出通道OC数量相同。 卷积核大小可适配本文所选F(2×2,3×3)卷积算子,无需预处理操作,与输入特征图划块匹配传入Winograd卷积算子运算。

3) 输入特征图划块和卷积核进行输入转置、卷积核转置、点乘和输出转置步骤。

4) 输入特征图与对应卷积核运算结果累加得到首个输出通道特征图。 每个输出通道特征图由F(2×2,3×3)卷积算子输出的2×2特征矩阵构成,数量为(W/2)2。 输出通道数量与卷积核个数相等。 卷积核与对应输入特征图运算结果聚集为输出特征图矩阵(如图1)。 VGG16模型卷积步长为1,卷积核为3×3,单个传统卷积计算需9次乘法,F(2×2,3×3)卷积算子运算包含4次传统卷积,乘法总量为36。 使用Winograd算法计算F(2×2,3×3)卷积算子时,4×4输入和3×3卷积核转置后都为尺寸4×4的矩阵,然后两矩阵对应点乘,需16次乘法计算,最后经输出转置过程得到与传统卷积等价的2×2输出。 本文使用Winograd算法运算F(2×2,3×3)卷积算子需16次乘法,相比传统卷积的36次乘法,节约率达55.56%。

2 CNN加速器设计

2.1 CNN加速器系统架构

基于Winograd算法的神经网络加速器系统架构如图2所示,CNN模型处理部分由FPGA片上完成,数据存储至片外动态随机存取内存(dynamic random access memory,DRAM),两者通过高级可扩展接口协议(advanced extensible interface,AXI)通信。 加速器由系统控制模块、输入缓存模块、权重缓存模块、维度转换模块、输入转置模块、权重转置模块、运算处理单元(process element,PE)、输出转置模块、最大池化模块、量化模块和输出缓存模块构成。 开发板上电启动时,模型参数和图片数据从安全数码卡加载至DRAM中,数据准备完成后,CNN加速器开始工作。 每轮计算将部分输入特征图和权重数据通过AXI4总线接口传入片上缓存单元,加速器循环处理剩余数据。

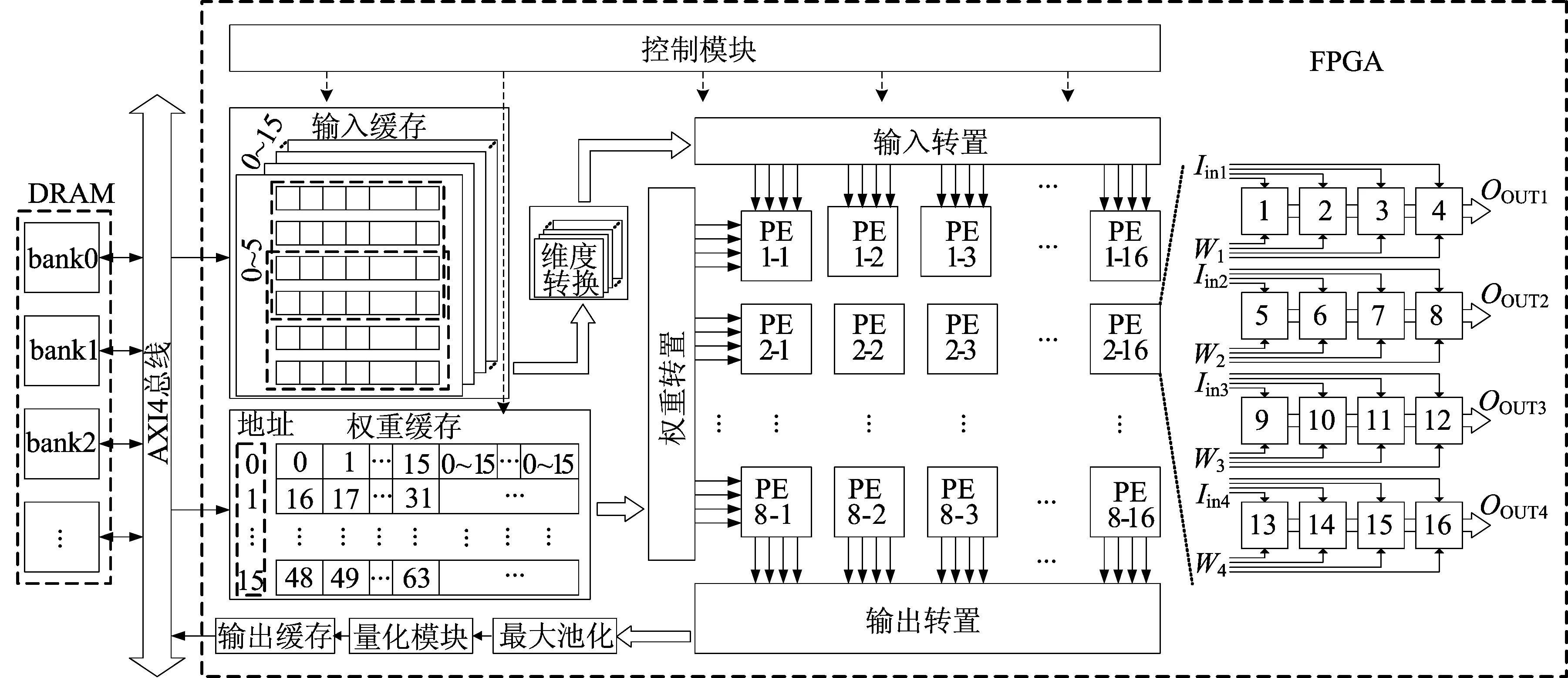
图2 CNN加速器整体架构

硬件加速器工作步骤如下:

1) 输入特征图缓存用双缓冲区策略[17],部分行数据预存至输入缓存模块,经维度转换模块后,二维输入数据块传入转置模块线上转置,输入转置模块由加法器和移位寄存器构成,所用系数与输入转置矩阵中元素一致。

2) 权重缓存由256个片上随机存储器块(block random access memory,BRAM)构成。 每周期提供256组输入通道权重,每个运行周期可处理16个卷积输入通道和16个输出通道,与处理单元阵列规模对应,存储块可提供处理单元每个周期计算所需权重参数。

3) 输入转置模块和权重转置模块将数据转置,广播至处理单元进行点乘运算。 每个处理单元由16个DSP与LUTs组成的乘法器组成,与本文 Winograd卷积算子所需16个乘法操作匹配。 本文二维处理单元每个运算周期执行一组点乘运算,相比一维计算单元缩短了等待周期,提高了加速器运行吞吐率。

4) 处理单元运算结果以二维形式广播至输出转置模块,进行输出转置,该模块转置矩阵如式(9)所示。 转置后结果经通道累加后缓存,直至所有输入通道卷积循环运算完成,得出最终累加结果。 输出结果即为传统卷积等价结果。 后经最大池化、量化模块处理,通过AXI4总线接口传至外部DRAM缓存,作为后续卷积层输入特征图数据。

2.2 输入缓存与线上维度转换模块

卷积核参数经Winograd算法转置过程,存储容量增加。 为减少片上存储资源开销,本文采取线上转置模块[8]。 因为转置过程需二维计算,所以将缓存一维数据转为二维数据运算。

本文设计维度转换模块和双缓冲区缓存模块实现上述功能,维度转换模块由移位寄存器构成,如图3a所示。F(2×2,3×3)卷积算子输入划块为4×4且两划块间重叠长度为2,输入缓存模块用行缓存且2组相邻行缓存间共用2个缓存单元,此模块可同时输出4行数据对应划块纵向维度4,同时实现Winograd输入划块的数据复用,如图3b、图3c所示。

图3 移位寄存器数据流

移位寄存器完成输入划块横向维度4,以2个相邻输入块为例,移位寄存器每周期接收2个输入缓存的特征像素,并左移2位。 按此运行规则,2个等待周期后移位寄存器高4位,每周期输出一组有效特征块,与后续模块组合完成全流水线运算。 一组移位寄存器输出4列数据,4组相同移位寄存器输出4行划块,共同输出二维4×4特征划块。 根据F(2×2,3×3)卷积算子输入特征块重叠规律,设计输入缓存模块对数据进行垂直维度复用,维度转换模块实现水平维度复用数据。 片上内存占用率减少至58%。

2.3 部分积切割方法

经F(2×2,3×3)卷积算子转置后,输入特征图和权重8 bit数据增加至10 bit,即乘数为10 bit定点整数。 DSP乘法器位宽为27×18,若直接用此乘法器,则造成乘法器与数据位宽失配,导致硬件资源乘法器利用率降低。

为解决定点数位宽与DSP乘法器失配问题,本文设计部分积切割方法,硬件由DSP和LUTs组合电路实现,最大化利用乘法器位宽,提升乘法器资源利用率。

数字信号处理器支持单周期操作,计算2个8 bit定点整数乘法[18],但8 bit输入和权重数据经转置过程后,位宽增加至10 bit,单个DSP无法计算2次乘法。 本文利用部分积切割方法,电路由LUTs扩展模块与DSP构成,运算单元单周期可同时计算2次乘法,实现单周期多输出功能。 DSP部分积划分如图4a所示,LUTs部分积划分如图4b所示,完成的乘法运算为:

图4 部分积切割映射关系

MMult0=IW0=MMult0_P1+MMult0_P2+MMult0_P3,MMult1=IW1=MMult1_P1+MMult1_P2+MMult1_P3

(10)

其中:I、W两乘数为10 bit;式(10)结果为20 bit。 本设计将10 bit权重划分为8、2 bit 2个部分,2个8 bit权重部分与10 bit输入乘法由DSP完成,2个2 bit权重部分与10 bit输入乘法由LUTs组成扩展部分完成,乘法结果由部分积相加得出。

DSP与LUTs组合电路结构如图5所示。 2 bit权重与10 bit输入乘法由LUTs组成扩展单元计算,扩展单元的部分积运算由与门和寄存器实现。

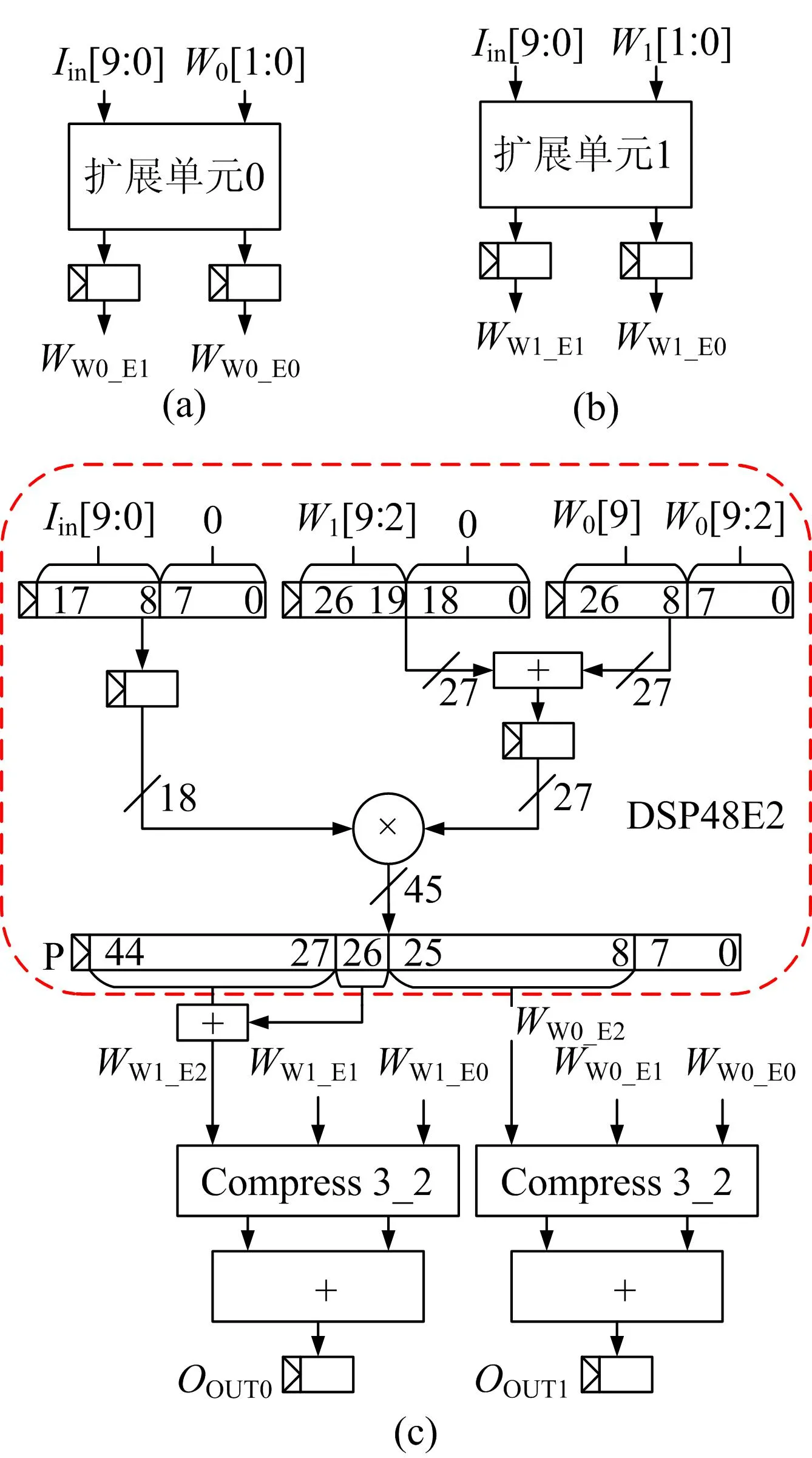
图5 DSP与LUTs组合电路结构

从图5a可以看出,第1个扩展单元输入卷积核0低2 bit,输出相乘的2个部分积WW0-E0和WW0-E1。 从图5b可以看出,第2个扩展单元输出卷积核1低2 bit,输出相乘的2个部分积WW1_E0和WW1_E1。 卷积核0乘法结果为W0对应的3个部分积之和,卷积核1乘法结果为W1对应的3个部分积之和。

从图5c可以看出,DSP中乘法器和预加器组合计算2个乘法,2个乘数分别为8 bit权重与10 bit输入。 将2个8 bit权重通过预加器拼接至乘法器27 bit输入端,10 bit输入低位补0后传至乘法器18 bit输入端,结果按输出端口P所示规则截取,DSP输出端口第8～25位为卷积核0的高8位与输入相乘结果,DSP输出端口第27～44位与第26位之和为卷积核1的高8位与输入相乘结果。

此外,本文设计部分和加法器采用华莱士树加法器,Compress 3-2使用全加器将3个部分积压缩为2个部分进行加法,有助于缩短关键路径延迟,减小电路建立时间违例概率,使系统运行稳定。

3 性能评估

3.1 软硬件平台速度对比

本文神经网络加速器与中央处理器(central processing unit,CPU)和图形处理器(graphics processing unit,GPU)平台速度对比见表2所列。

表2 不同平台速度对比

CPU和GPU平台的软件语言使用Python 3.7,机器学习库为Pytorch 1.12,指令集架构为CUDA 11.7。 本文所用中央处理器和图形处理器运行VGG16模型推理速度分别为640.11、65.87 ms。 本设计使用XCKU060 FPGA部署VGG16模型,工作频率达180 MHz,推理阶段卷积计算花费时间为19.12 ms。 相比Intel i5-4590 CPU和Nvidia GTX 1070 Ti GPU,本文硬件加速器卷积运算速度分别提升33.47、3.43倍。

3.2 硬件平台性能评估

本文将VGG16网络模型部署至XCKU060开发板,并评估加速器性能。 仿真验证和硬件实现EDA软件为Vivado 2021.1。 构建开发板评估环境,测试数据和网络模型权重数据预存至SD卡,开发板上电后控制器初始化系统,将测试数据和模型参数搬运至DDR。 其输入数据与权重参数为量化后8 bit定点整数。 开发板片上资源利用率见表3所列。

表3 FPGA片上资源利用率

本文设计与近年来相关工作性能的对比见表4所列。

表4 VGG16模型加速器性能对比

文献[6]使用大规模处理单元阵列提升硬件加速器吞吐量,使用DSP数量超出本文1倍,但Winograd卷积加速器[6]的性能仅比本文设计高0.11倍。 文献[7]将Winograd算法数据流调整与传统卷积数据流匹配,扩展加速器应用范围,但文献[7]计算数据位宽与硬件匹配度低,造成乘法器资源的效率仅为0.28。

文献[9]利用卷积核尺寸为3×3的算子,使用统一转置矩阵节约片上硬件资源。 但CNN加速器[9]选取8 bit定点数据,而设计中DSP无法高效利用低比特数据优势。

文献[11]使用乒乓操作提升DSP利用率,但是运算单元乘法器[11]输入端的位宽为27 bit,其位宽占用率仅为59%。 本文通过输入缓存模块和维度转换模块对数据复用,减少数据搬移,使加速器处理卷积层的平均吞吐率达2.358×1012OPs。 此外,采用部分积切割方法,充分利用DSP输入端的位宽,使CNN加速器每个DSP运算效率达109OPs,相比文献[9]、文献[11]分别提升了54%、29%。

4 结 论

本文面向FPGA硬件部署神经网络模型,提出一种基于Winograd算法高效部署CNN模型的加速器架构。 利用Winograd卷积算法代替VGG16模型中传统卷积算法,减少55.5%的乘法运算量。 通过将FPGA片上DSP与LUTs资源结合构成处理单元运算电路,实现部分积切割方法,具备单周期多输出特点,解决数据位宽与乘法器失配问题,提高乘法器利用率和处理单元运行效率。 实验结果表明,加速器运行VGG16模型卷积层的平均吞吐率和每个DSP运算效率分别为2.358×1012OPs和1.15×109OPs。