一种改进SLO的多目标服务优化组合方法①
2024-01-06刘志中
海 燕, 徐 芯, 刘志中
(1.华北水利水电大学信息工程学院,河南 郑州 450046;2.烟台大学计算机与控制工程学院,山东 烟台 264005)
0 引 言
随着云计算的持续发展及用户需求不断增加,服务组合在网络技术研究领域发挥着愈加重要的作用。庞大的候选服务数量、相互冲突的优化目标给服务优化组合问题带来了巨大的挑战。因此,如何高效地从海量组合服务方案中选择最优的组合服务,是服务计算领域中一个重要的研究问题。最初服务优化组合问题被建模为单目标问题[1],或者将多个目标转化为单目标问题[2]。随着多目标优化技术的进步,越来越多的研究致力于使用群体智能算法(例如:人工蜂群优化算法[3]、粒子群优化算法[4]、蚁群优化算法[5]等)来解决服务优化组合问题。针对服务组合的多目标性与用户需求的复杂性,设置多个相互冲突的优化目标及约束条件,在此基础上,改进社会学习优化算法(Social Learning Optimization Algorithm, SLO)中的关键操作算子,引入Sigmoid扰动学习因子,最终形成一种基于改进社会学习优化算法的多目标服务优化组合方法(improved Social Learning Optimization-multi-objective service composition optimization, ISLO-MOSCO),最后通过实验验证了该方法的有效性。
1 多目标服务优化组合问题模型


表1 组合服务的QoS计算方法

选取在服务组合中相互对立且较为重要的三个QoS属性作为优化目标,依次为成本、响应时间与可靠性。根据表1将服务优化组合问题建模成多目标优化问题,规定全局约束条件为总费用不超过Cmax,响应时间不超过Tmax,可靠性不低于Relmin,则多目标服务优化组合问题的数学模型如式(1)所示,其中,x={x1,x2,...,xn}是决策空间Ω中的n维决策向量。
minF(x)={f1(x),f2(x),f3(x)}s.t.x∈ΩfC(x)
(1)
为了评估解的优劣,采用Pareto支配概念计算多目标优化算法的适应度值[3]。如果Individual1≻Individual2,则认为Individual1优于Individual2,则该解在种群中的支配解数dom(i)加1,该解的适应度值计算方式如式(2):
(2)
2 基于改进SLO的多目标服务优化组合算法
2.1 改进的SLO算法
2.1.1 组合服务编码模型
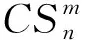
2.1.2 微空间内的操作
SLO算法的微空间模拟人类社会智能演化过程受遗传变异影响的现象,通过选择操作、交叉操作和变异操作来实现遗传变异的进化过程。对于多目标服务优化组合问题,采用轮盘赌的选择方法作为选择算子,另外两个操作定义如下。
2.1.2.1 交叉操作
设Xi=(xi1,...,xik,...,xin)与Xj=(xj1,...,xjk,...,xjn)为任意两个个体,i,j∈{1,...,N},N为种群规模,且i≠j,n表示服务组合流程中子任务的序号,xik,xjk∈{1,2,3,...,m}。利用rand函数生成1~m之间的随机交叉点位,r为(0,1)的随机数,pc为交叉率,若r (3) 图1 组合服务编码方式 2.1.2.2 变异操作 设Xi=(xi1,…,xik,…,xin)为种群中任一个体,i∈{1,…,N},N为种群规模,在当前个体的染色体中,根据变异率pm随机选择一个变异基因点,假设xik为变异基因点,xik∈{1,2,3,…,m},利用随机函数在{1,2,3,…,m}范围内随机生成一个新的基因xil替换变异个体中变异点的基因xik。变异操作如式(4): (xi1,…,xil,…,xin) (4) 2.1.3 学习空间内的操作 2.1.3.1 观察学习 (5) 2.1.3.2 模仿学习 (6) 2.1.4 信仰空间内的操作 2.1.4.1 知识更新 知识更新操作主要是当学习空间得到新的优秀个体时,对信仰空间内的个体实现知识的更新与积累。更新操作公式如式(7): α=N*β (7) 式(7)中,α指当前群体中需要选择优秀个体的数量;N表示种群规模;β为选择概率。 2.1.4.2 文化影响 文化影响操作是使用信仰空间内的知识影响微空间内非支配排序等级较低的个体,引导群体向较好的方向演化,提高算法的收敛速度,公式如式(8): (8) 式(8)中,Xi=(xi1,...,xik,...,xin)为种群中的任一个体,i∈{1,...,N};aj为信仰空间中的任意个体,j∈{0,...,α},α为信仰空间内的个体数量;t是当前迭代次数;ε为更新间隔参数。 2.1.5 修正操作 通过观察学习与模仿学习产生的新个体中,由于所有个体的每一维变量的取值都为子任务对应的候选服务的序号,若第k维变量的值超过了其取值范围,则根据以下公式修正该维变量的值,其中m为子任务对应的候选服务总个数。 (9) 针对服务优化组合问题的特点对SLO算法进行了改进,形成了一种面向多目标服务优化组合问题的求解方法。综上,基于改进社会学习优化算法的服务组合优化算法(ISLO-MOSCO)具体实现步骤如下: Step1.设置算法参数:初始化算法参数,包括种群规模N,最大迭代次数Max_Iteration,变异概率Pm,交叉概率Pc,信仰空间内的个体数量α和更新间隔参数ε,同时初始化QoS属性。 Step2.初始化种群对种群进行非支配排序。 Step3.在微空间内,对个体进行选择操作、交叉操作以及变异操作,并保留优秀个体。 Step4.在学习空间内,对个体进行观察学习操作与模仿学习操作,并保留优秀的个体。 Step5.在信仰空间内,利用学习空间得到的优秀个体对信仰空间内的个体进行知识的更新与积累,并使用信仰空间内的知识影响微空间内非支配排序等级较低的个体。 Step6.重复Step3-Step5,直至达到最大迭代次数Max_Iteration。 为了验证所提多目标服务优化组合方法的性能,实验主要从以下四个方面展开:(1)验证所提方法在不同迭代次数下求解多目标服务优化组合问题的可行性;(2)验证所提方法在不同问题规模下的适应性;(3)所提ISLO-MOSCO算法与其他算法的性能对比;(4)验证对SLO算法提出的改进策略的有效性。 基于上述提出的多目标服务优化组合方法,设置每个候选服务都具有三个QoS属性,即成本、响应时间、可靠性。实验采用随机数据集,将每一组实验分别运行20次,选取20次测试结果的平均值作为最终实验结果。 实验使用Java编程语言实现了基于改进SLO的多目标服务优化组合方法,其中交叉概率设置为0.85,突变概率设置为0.05,知识更新选择比例设置为10%,文化影响更新间隔设置为5。实验环境配置为PC,11th Gen Intel(R) Core(TM) i5-1135G7 @ 2.40GHz 2.42 GHz,Windows 10(64bit)。 设置子任务数量固定为10,将子任务对应的候选服务数量分别设置为10,20,50,100,200。执行ISLO-MOSCO算法,记录算法在不同迭代次数下的运行时间。实验结果如图2所示,横坐标表示算法的迭代次数,纵坐标表示算法的运行时间,m表示每个子任务对应的候选服务的数量。 图2 不同候选服务数量下的运行时间 从图 2可以看出,ISLO-MOSCO算法的运行时间随迭代次数的增加而增加,存在上下波动的情况。ISLO-MOSCO算法的运行时间与不同的候选服务数量没有明显的相关关系,此外,随着候选服务数量的增加,算法的运行时间并没有呈指数级增长。因此,可以得出ISLO-MOSCO算法对于解决多目标服务优化组合问题是可行的。 通过设置不同的子任务的数量和不同的子任务对应的候选服务数量,从而设置不同的问题规模。设置五种问题规模,其子任务数量和候选服务数量分别为5*10,10*20,20*50,30*100,50*200。迭代次数设置为1000,执行ISLO-MOSCO算法,记录算法在不同问题规模下求解多目标服务优化组合问题得到的组合服务解集的QoS值。实验结果如图 3所示,cost,time,reliability分别表示组合服务解集的成本、响应时间与可靠性。 图3 不同问题规模下解集的QoS值 从图 3可以看出,ISLO-MOSCO求解多目标服务优化组合问题得到的组合服务解集的成本与时间随问题规模增大而减小,这是因为当问题规模增大时,构成组合服务的数量也在增大,可以给算法提供更多更好的选择。当问题规模由5*10增加到20*50时,解集的可靠性不断增加。当问题规模由20*50增加到50*200时,解集的可靠性不断降低,表示解集的可靠性随问题规模增加而具有一定波动性。服务组合解集的成本与响应时间没有随问题规模的增大而指数性减少,甚至有所增大,可靠性也没有随问题规模的增大而指数性降低。因此,可以得出ISLO-MOSCO算法对于解决多目标服务优化组合问题具有一定的适应性。 采用NSGA-II[8],GA[9],MOEA/D[10]和ISLO-MOSCO算法求解相同的多目标服务优化组合问题。将四种算法的子任务数量设置为10,子任务对应的候选服务数量设置为50,初始种群大小设置为100,记录四种算法在不同迭代时间下搜索到的组合服务方案解集的适应度值,实验结果如图 4所示。 图4 算法性能比较 从图 4可以看出,ISLO-MOSCO比NSGA-II算法、GA算法和MOEA/D算法有更快的收敛速度,并且ISLO-MOSCO得到的最终解优于其他三种算法。基于上述实验结果可以得出结论,对SLO提出的改进是有效的,ISLO-MOSCO对于多目标服务优化组合问题是有效的。 在未改进的SLO中,修改其初始化方式、目标函数以及约束条件,使其能够解决多目标服务优化组合问题,将SLO与ISLO-MOSCO进行比较。将两种算法的子任务数量设置为10,子任务对应的候选服务数量设置为50,初始种群大小设置为100,迭代次数设置为1000,记录两种算法在不同问题规模下搜索到的组合服务解集的适应度值,实验结果如图 5所示。 图5 验证SLO改进策略的有效性 从图 5可以看出,ISLO-MOSCO得到的解优于SLO。随着问题规模的增加,ISLO-MOSCO与SLO算法得到的解集的QoS值的差距不断增大。基于上述实验结果可以得出结论,针对SLO算法提出的改进策略是有效的。 在考虑服务组合特点与用户需求的情况下,如何为用户选择最优组合服务方案这一关键难题,主要可以从以下两个方面进行总结:(1)基于社会学习优化算法,设置多个相互冲突的优化目标、约束条件及取值空间,引入Sigmoid扰动学习因子,改进算法中的关键操作算子,使得改进的社会学习优化算法能够有效求解多目标服务优化组合问题;(2)针对研究问题与改进的社会学习优化算法提出了新的多目标服务优化组合方法,基于随机数据集,将所提多目标服务优化组合方法与四种服务组合方法进行对比,验证了改进的SLO算法能够更好地求解服务优化组合问题。在未来的研究中,将考虑动态环境下的服务组合问题以及如何设计环境变化响应策略,以此实现动态多目标服务优化组合。


2.2 ISLO-MOSCO算法整体流程
3 仿真实验及结果分析
3.1 实验设置
3.2 验证不同迭代次数下ISLO-MOSCO的性能
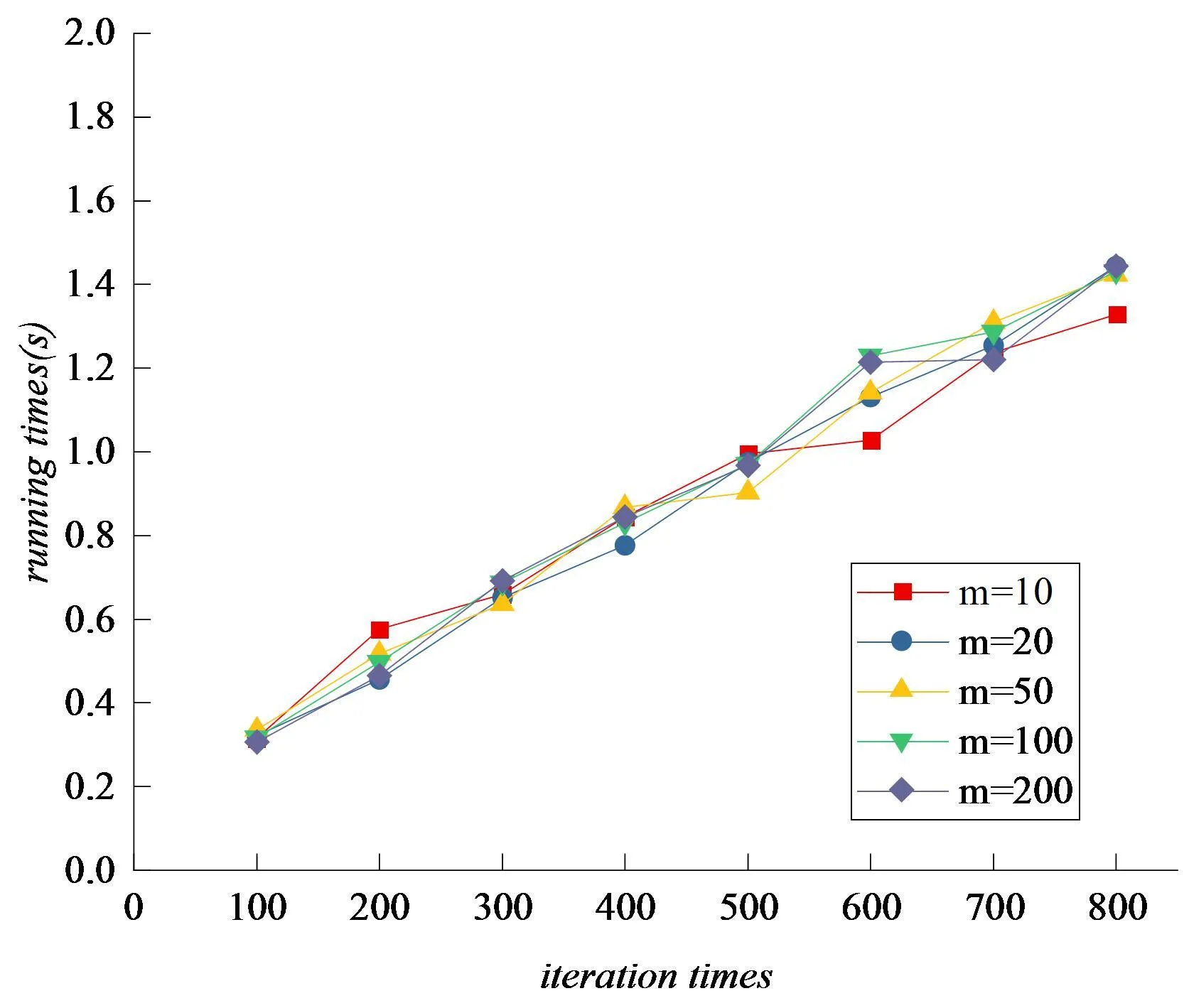
3.3 验证不同问题规模下ISLO-MOSCO的性能
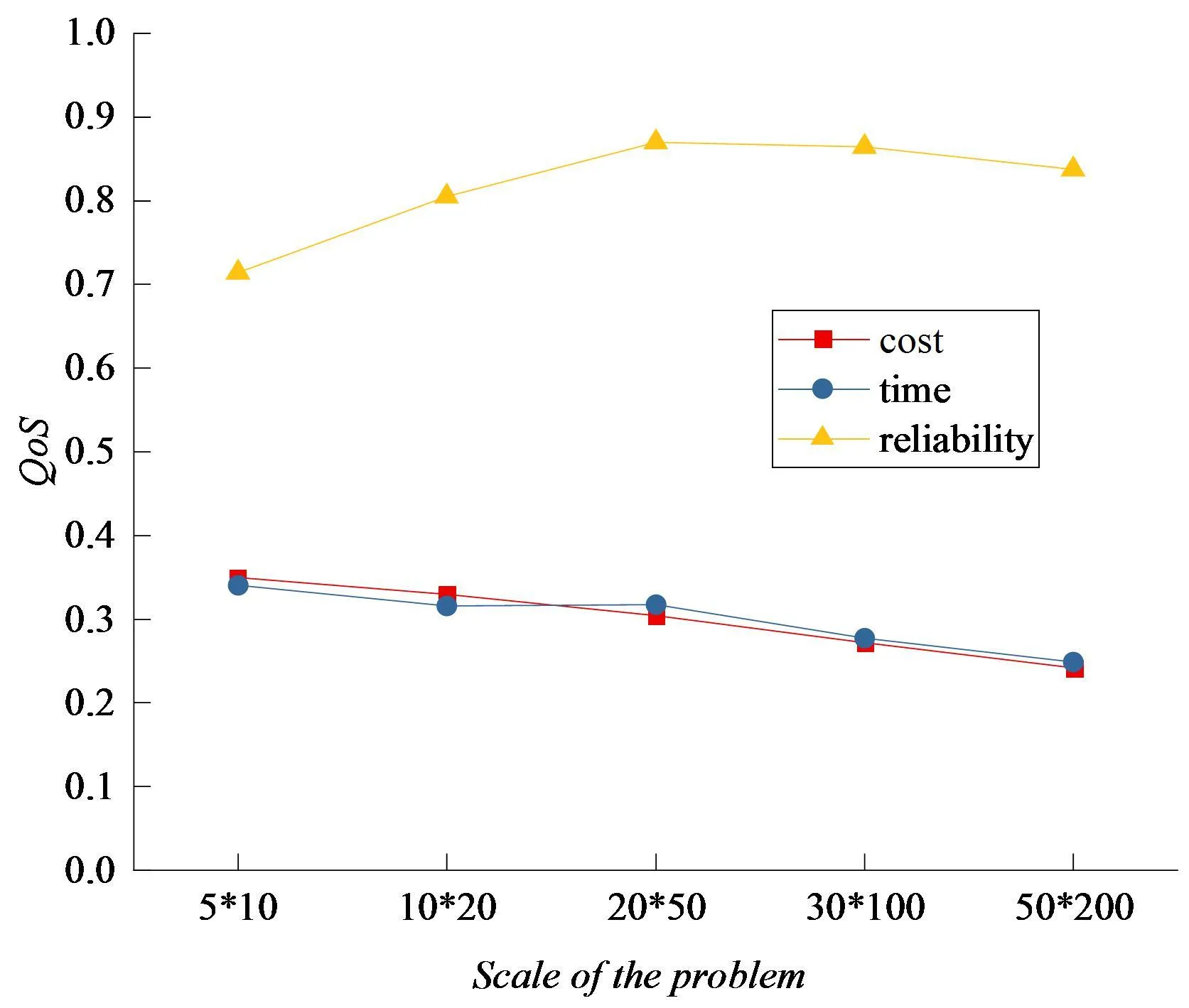
3.4 ISLO-MOSCO算法性能对比

3.5 验证提出的SLO改进策略的有效性

4 结 语
