关于无线可充电传感器网络充电路线规划的研究分析①

史长青, 喻 俊

(中原工学院彼得堡航空学院,河南 郑州 450007)

0 引 言

无线传感器网络[1]中包括若干传感器以及一个数据中心,传感器从环境中收集信息后每隔一段时间将收集到的信息发送到数据中心。传感器正常工作的前提是需要有移动充电器提供满足其使用要求的电能,出于对移动充电器的能量利用效率的考虑,在移动充电器匀速行驶的前提下需要尽量减少移动充电器的行驶路程,所以优化充电线路是提高充电器能效比的关键所在。在优化充电线路时,当给出节点的经纬度且只有一个充电器进行工作时,如何规划充电线路才可以实现路上的能效降到最低是研究的核心问题。围绕着无线可充电传感器网络充电路线规划的建模分析,首先建立了无线网络分布的线路模型,利用python中的geopy库将经纬度转化为距离数据,再利用贪婪算法计算运行路径的最优解,在面对电池容量最优问题时,以移动电源走完一个回路后电池容量刚好达到最低为最优条件,用数值解法结合约束条件求得数值解结果,四车移动充电情况可以视为有时间窗车辆路径问题(vehicle routing problems with time windows),求得其最小化的优化值即为最优路径选择。

常用的移动充电规划框架具体过程如图1所示,网络中的传感器是随即部署的,因此需要通过聚类算法得到合适充电的充电停留位置。由于无线传感器属于一个微型网络且分布有多个节点,所以在进行路径优化之前首先需要的就是对节点进行分簇处理以此来获取到停留点,将所有的停留点串联起来也就是所说的充电线路。通俗地说,充电线路优化也就是我们常见的带有约束的TSP问题[2],通过对其求解可以获得移动充电器的充电路径,再选取移动充电器合适的充电方案对网络中的传感器节点进行充电。

图1 移动规划步骤

.

1 理论原理

无线充电传感器具体单对单、单对多两种充电模式。对于前者来说是利用一个充电器对一个网络节点进行充电;对于后者来说,是利用充电器对网络中的多个节进行充电的过程,而且由于每个节点距离基站的距离不同,节点的充电顺序也不一样。在对多个节点充电之前,首先需要在基站中完成充电器的电能补充操作,然后根据距离大小先对距离基站最近的节点进行充电并将其视为初始充电节点,完成之后对下一个节点进行充电并以此类推。但是要实现总充电量最小时,移动充电器必须访问每个传感器节点一次,而且不重复并最后返回到初始充电节点,形成一个封闭回路,要使移动充电器的行驶路径最短问题,就是一个典型的TSP问题。

TSP的实质就是路径规划问题,它又被称为旅行商或者旅行推销员问题,举例解释为:有多个城市需要商人途径且只能途径一次,如何对路径进行合理的规划才能实现路途最短。这一TSP问题的求解方式就是需要将所有的目标点进行全排列即可,虽然方法笨拙可行,但当目标点的数量过多时,其计算步骤与难度也会成指数倍增加,属于NP完全问题,故该方法不可取。

对于无线充电路径优化问题来说就如同求解TSP问题一样,网络中的节点就是旅行商途径的城市,每两个节点连接成一条线并具有相应的距离。如果将所有的连线类比成树枝,那么整个网络就成了树,树根节点也就是充电起始点。在进行最佳路径求解时可以根据贪婪算法,首先对节点进行处理并根据邻边最短原则将节点进行串联起来,然后将满足要求的边视为初始路径供后续使用。当在优化计算时,一步一步将每个节点连接起来最终形成一颗完成的书,也就类似于商人途径过所有的城市,根据这一方法获取到的树其路径是最短的。最后可以根据深度优先原则对整个树进行查找,最终获取到符合要求的路径。

2 算法步骤

算法方面or-tools库提供了两种思路,第一种思路是是基于启发式算法[3]的策略(first solution strategy),这一策略的优点在于搜索的速度比较快,相应的缺点是:这一方法寻找的解只是相对意义上的优秀解,不能保证结果是最优解。第二种思路是启发式+元启发[4]的算法,这一算法在初始解的生成过程用启发式算法计算,后续的元启发过程在这个解上进行。这一算法搜索时间会相对长一些,但搜索得到的相对最优解要优于基于启发式搜索的解法。

采用了or-Tools库给出了最优解和次优解。两种算法思路:第一解算策略算法(first solution strategy)和引导式本地搜索算法,通过Python的程序包组合,使得在程序里设置一个选择参数就能转换算法模式,对比两种算法的结果后可以得出理论上的最优解。

但是对于第一解算策略算法来说,因为程序的选择策略问题只能得到一个相对意义上的优秀解,有是最优解的可能性,将其结果与引导式本地搜索算法的结果相互对比印证,主要使用引导式本地搜索算法来解决问题。为了便于求解,先利用python中谷歌开发的geopy库将经纬度数据转化为距离数据,把问题转化为从数据中心出发遍历所有传感器位置后再回到数据中心的最短路径问题。

贪婪算法[5],又称贪心算法(Greedy Algorithm)。对于该算法而言,之所以称之为“贪婪”,是因为它不考虑后续过程的影响,而是将最有利于本次计算的参数作为最佳选项进行求解,最终获取到局部最优解。该算法侧重于当前状态的选择,忽略了后续影响,故无后效性是其最大的特征。

在求解TSP问题时可以使用贪婪算法进行,具体步骤为:首先在多个城市中随机挑选一个作为初始参考对象,然后以其为中心进行下一个城市的选择,而且要保证每次选择的城市距离初始参考对象的距离应最小,当所有的城市选择完之后,本次求解过程终止。在选择城市的时候,不考虑后续的影响,只考虑满足本次要求的城市,也就是说本次选择的城市路径距离最短。虽然通过上述方法不能获取到最佳路径,但在一定程度上简化整个计算过程。而且这一方法更加适用于目标(城市)数量较少的问题,该方法得到的路径长度通常情况下不大于最佳路径的1.15倍。

要使用引导式本地搜索算法来解决问题,必须为给定问题定义解决方案功能。定义解决方案特征以区分具有不同特征的解决方案,以便可以识别和避免围绕局部最优的相似区域。解决方案功能的选择取决于问题的类型,并且在某种程度上还取决于本地搜索算法。对于每个功能Fi定义为一个函数Ci。每个功能Fi与一个惩罚函数Pi相关联,以局部极小值记录要素出现的次数,而功能函数直接来自于目标函数。例如,在旅行商问题中,“旅行是否直接从城市X到城市Y”可以定义为要素。X和Y之间的距离可以定义为成本。

在实现级别,为每个功能定义一个指标功能,指示当前解决方案中是否存在该功能。当指示值解为1时该功能成立,值为0时该功能不成立。

在算法步骤之前先对相应对的物理量和数学符号作出如下说明:

表1 符号说明

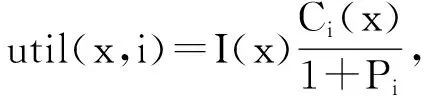
上述流程可以归结为以下步骤:

第一步:通过Python的geopy库将经纬度数据转化为距离数据并存储在数组数组{LA1A2}中,在数组基础上建立距离矩阵,若用distances表示两点间的距离。那么该问题本质上就是从初始点0出发,经过所有的点最终回到初始0并使得途径路径最短。求解空间就是利用Python算法中的geopy库对矩阵中的经纬度进行换算,实现所有点的排列组合并得到最佳的距离矩阵。

第二步:运用Python的or-Tools的RoutingModel解决TSP问题。

第三步:传入一个计算距离的回调函数,设定初始可行解的求解方案为first_solution_strategy(选项为PATH_CHEAPEST_ARC)和Local_search_options(选项为GUIDED_LOCAL_SEARCH),就可以使用SolveWithParameters进行求解[6]。

3 实验及结果分析

算法在Python的IDE上编程,在PC机上已经实现,程序通过上述算法步骤实现了对最优路径的规划情况,第一解算策略算法得出的结果如图2所示:

图2 启发式搜索路径结果

图3 移动充电器模拟运行图(启发式)

引导式本地搜索算法得出的结果如图4所示:

图4 引导式+元启发路径结果

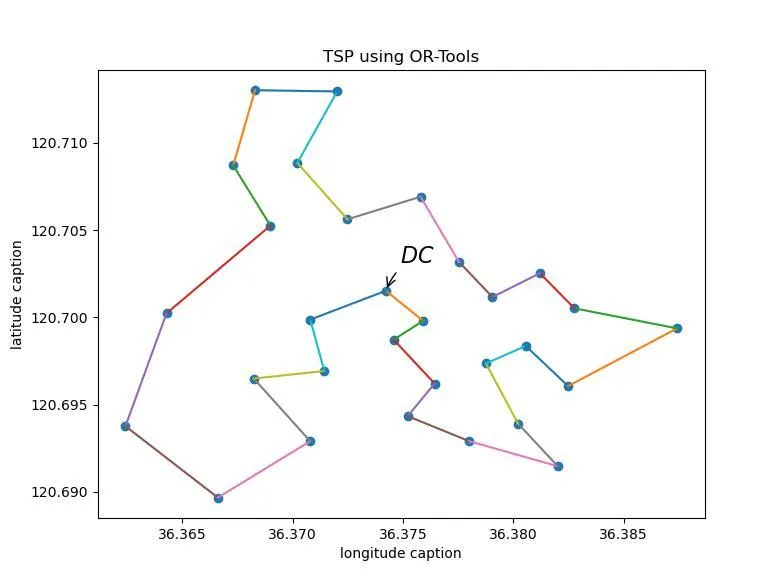
图5 移动充电器模拟运行图(启发式+元启发式)

如图2所示,第一解算策略算法(启发式搜索)路径结果为:0 -> 2 -> 1 -> 9 -> 7 -> 6 -> 11 -> 14 -> 15 -> 27 -> 16 -> 13 -> 12 -> 8 -> 10 -> 5 -> 3 -> 28 -> 24 -> 23 -> 29 -> 26 -> 25 -> 18 -> 19 -> 20 -> 17 -> 21 -> 22 -> 4 -> 0,得出的移动充电器移动最短距离为12033 m。而图2是启发式搜索路径结果图。

如图4所示,引导式本地搜索算法(启发式+元启发式搜索)路径结果为:0 -> 2 -> 1 -> 9 -> 7 -> 6 -> 14 -> 11 -> 8 -> 12 -> 15 -> 27 -> 16 -> 13 -> 10 -> 5 -> 3 -> 4 -> 22 -> 28 -> 24 -> 23 -> 21 -> 29 -> 26 -> 25 -> 18 -> 19 -> 20 -> 17 -> 0,得出的移动充电器运行的最短距离为11469 m。而图5是启发式+元启发式搜索路径结果图。

对比以上结果发现,采用基于贪婪算法的引导式本地搜索算法可以得到的路径选择是理论上的最优路径选择。

4 结 语

进行无线充电路径优化计算时,将路径图视为网络结构图进行,并将传感器的经纬度与地球半径结合起来获取到每两个节点之间的距离。然后将问题转化为找到一个从数据中心出发,依据现有路径遍历网络图的每一个节点后再回到数据中心的最短路径问题。在贪婪算法的基础上逐步进行求解,最终获取到最佳路径,使得充电器在充电时能效最小。