推移式土质滑坡下输气管道力学响应及路由优化分析

兰旭彬,蒋宏业,杨雅冰,朱海瑞,赵连学

(1. 中石化石油工程设计有限公司成都分公司,四川 成都 610031; 2. 西南石油大学 石油与天然气工程学院,四川 成都 610500;3. 中石化石油工程设计有限公司,山东 东营 257100; 4. 山东莱克工程设计有限公司,山东 东营 257100)

0 引言

伴随国家石油天然气管网集团有限公司的成立,主要油气管道实现“并网运行”,“全国一张网”框架基本形成;同时围绕“双碳”战略目标部署及充分落实“十四五”规划要求,油气管道等基础设施建设迎来快速发展时期[1]。管道在进行敷设时,不可避免地受到绕避城乡规划区、环境敏感区等因素影响,而穿越滑坡区,伴随岩/土体大位移作用,致使管道受到挤压、剪切等非设计载荷作用,使其裸露、悬空,甚至屈服、断裂,对油气资源的安全输送带来挑战[2-3]。

针对滑坡下管道受力分析的实现,其重点在于管土耦合作用的实现,目前常采用弹性地基梁模型、土弹簧模型及非线性接触模型。朱勇等[4]在试验研究基础上,基于Winkler假设,将土体简化为接地弹簧单元,忽略了土体变形的连续性。HAN等[5]针对滑体内/外分别采用PSI/土弹簧模型,间接实现管土相互作用,其模拟结果精度取决于弹簧布设密度及其刚度选取。张伯君[6]基于非线性接触模型,辅以位移驱动,综合考虑材料、接触和几何非线性,实现管土耦合过程中的滑移与分离。FREDJ等[7-8]针对离散土体颗粒大位移所引起的模拟求解难题,首次在非线性接触模型基础上,引入光滑粒子流体动力学法(SPH),并与传统有限元法(FEM)进行耦合,实现了土粒子非线性大变形作用下管道力学分析;随后,蒋宏业等[9]基于SPH-FEM耦合算法,实现土-管-油多物理场耦合分析;徐涛龙等[10]基于粒子法,分别以泥石流、滑坡等典型地灾为研究对象,对管道力学规律给予分析,实现了管土耦合研究多元化的目的;YI等[11]建立滑坡灾害下含缺陷管道力学分析模型,考虑缺陷位置、数量等因素影响。

当管道路由穿越滑坡区时,通常以绕避为主,但对于影响区内不可绕避路由选取并未提供过多的参考建议。因此,在此研究背景下,从设计的角度出发,笔者基于SPH-FEM耦合算法,结合非线性接触模型,首先针对不同管径建立滑坡模型,获取土体大位移下管道力学规律,为运维期滑坡区管道监测位置选取提供建议;其次在对管道敷设滑体内、外不同位置模拟分析基础上,考虑壁厚、埋深因素带来的影响,并基于应力/应变准则加以评判,为设计阶段滑坡影响区内不可绕避管道路由选取提供优化措施。

1 滑坡下管道力学响应分析

1.1 模型建立

利用ANSYS/LS-DYNA软件建立滑坡作用下输气管道力学分析全尺寸耦合模型[6],相关尺寸如图1所示,其中滑坡宽30 m,管径分别选取φ1219 mm×22 mm、φ273 mm×10 mm,埋深均为1.2 m,敷设于滑体中部。并依据滑坡尺寸及滑土因重力而产生的下滑速度,估算模型计算所需截止时间为1×106μs,时间步长采用默认设置。针对于载荷及边界条件,考虑模型整体自重载荷及管内压10 MPa,并在模型底部施加全位移约束及四周无反射边界。针对于管土相互作用实现,本文采用非线性接触模型[12-13],其原理是在管-土的交界面处通过定义接触面的形式实现运动方程等信息的传递,优势在于能够对管土之间的滑动与分离进行仿真模拟。

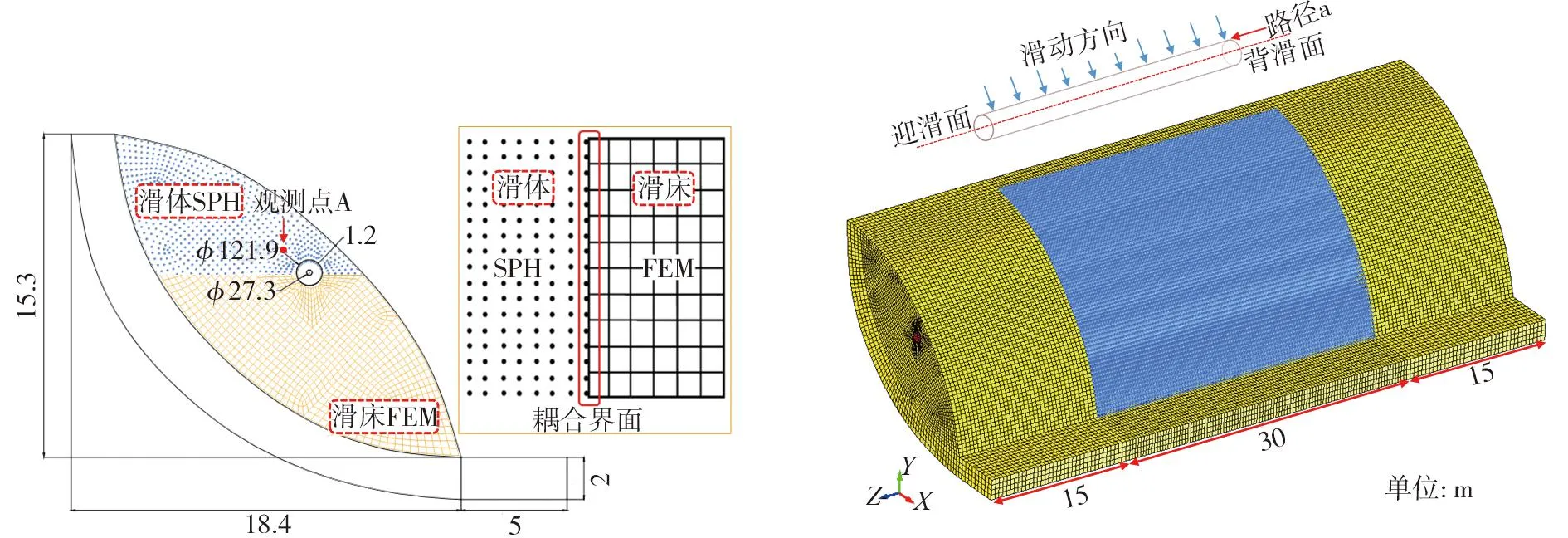
图1 滑坡尺寸及SPH-FEM耦合模型Fig. 1 Landslide size and SPH-FEM coupling model

在模拟过程中,综合考虑材料、几何及边界非线性影响,同时为避免传统网格法因大变形问题所带来的模拟求解难题,本文引入无网格、拉格朗日、质点性质的光滑粒子流体动力学法(SPH),其本质是将粒子点上的值以积分插值形式计算得到密度、压力等宏观物理变量f(x),并利用粒子近似方法将其离散化[14-15],其精髓在于“以空间运动的质点为计算单元[16]”。同时为便于模型周界处理,并提高计算效率,在小变形区域采用网格法,即滑体区域SPH粒子化,滑床及管道区域FEM网格化;并在网格尺寸无关性验算基础上,选取FEM网格尺寸为30 cm,而SPH粒子是在网格基础上生成的,即粒子间距同样为30 cm。管道与土体本构模型分别选取随动硬化双线性弹塑MAT_PLASTIC_KINEMATIC模型、修正的Mohr-Coulomb屈服准则的MAT_FHWA_SOIL模型,相关参数选取参考表1,相关表达式如式(1)～式(2):

表1 管道、滑体及滑床材料参数Table 1 Material parameters of pipeline, sliding mass and sliding bed

(1)

(2)

式中:p为压力(MPa);K(θ)为应力罗德角函数;φ为内摩擦角(°);c为内聚力(MPa);J2为应力偏张量的第二不变量(MPa2);Ahyp为屈服面间相似因数(MPa)。

1.2 管道失效准则

针对管道失效与否的判断,通常采用基于应力设计准则,即管道在外载作用下所产生的最大应力小于管材自身最小屈服强度,此种方法曾为管道安全运行提供较好的保证。但随着管道建设的快速发展,管材延性的提高,在一定塑性变形下,仍能满足运行安全;且伴随着滑坡、断层等地灾区管道敷设,管土间存在以大位移载荷为主的耦合作用,此时应力设计准则过于保守,为充分发挥管材性能,基于应变设计准则应运而生。因此,本文基于应力、应变准则,对管土耦合作用下管道受力情况给予判定。

对于应力设计准则,本文选取第四强度理论,相应计算公式为:

(3)

式中:σMises为等效应力(MPa);σ1为第一主应力(MPa);σ2为第二主应力(MPa);σ3为第三主应力(MPa);[σt]为许用应力(MPa)。

管道受压缩、弯矩等载荷作用下,易致使管道发生局部屈曲或褶皱,因而对于应变设计准则,本文选取临界屈曲作为评判标准,并根据不同模型工况给予临界纵向应变值,其相关数据如表2所示,相应计算公式为:

表2 临界纵向压应变Table 2 Critical longitudinal compressive strain

(4)

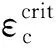
1.3 滑坡下管道受力分析

选取图1中路径a,获取观测点A处土体(与管道距离1.2 m)不同位移下管道轴向位移曲线。由图2可知,当管道横坡敷设时,在滑土下滑力作用下,滑体中心截面处管道位移值最大,整体呈现典型“鞍”状;管径为1219 mm时,其轴向位移曲线平缓过度,当滑土位移为30、42、54 cm时,其最大值分别为29.76、42.44、54.57 cm;而管径为273 mm时,在滑体周界处,管道位移量发生突变,易受滑床阻碍而发生剪切破坏,两侧管体位移趋于稳定,当滑土位移为28.6 cm时,滑体内管体位移为27.22 cm,滑床内位移为4.92 cm;将管道最大位移与滑土位移对比发现,二者并无线性关系,即管土耦合过程中存在滑移与分离,呈现非线性。

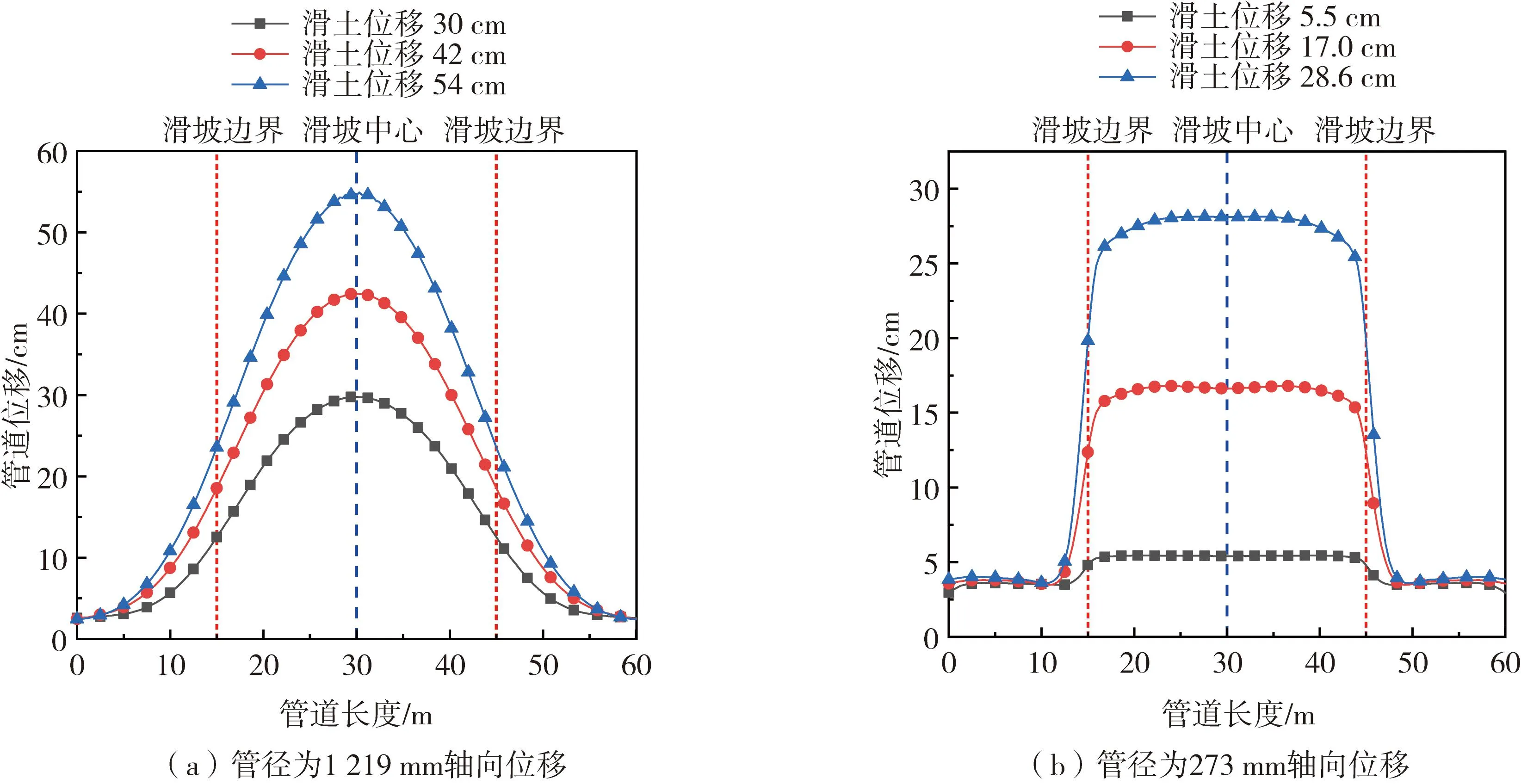
图2 不同滑土位移下管道位移曲线及云图Fig. 2 Displacement curves and nephogram of pipeline under different sliding-soil displacements

获取路径a下管道轴向应力曲线,由图3(a)可知,当管径为1219 mm,其应力极值出现在滑体中心截面处,当滑土位移54 cm时,其值为550.36 MPa,整体未发生屈服变形,此时管道纵向应变极值为0.29%;当滑土位移为42、30 cm时,其应力值同比减少了7.30%、24.56%。由图3(b)可知,当管径为273 mm时,在滑体周界两侧出现明显的应力集中区域,且应力极值位于滑体内,距离周界约0.6 m,当滑土位移为28.6 cm时,其应力极值为412.04 MPa,已发生屈服破坏,此时纵向应变极值为0.88%,小于临界应变值,满足安全要求;同时沿周界向滑体中心靠近时,其应力值较为平稳,约为127.14 MPa。

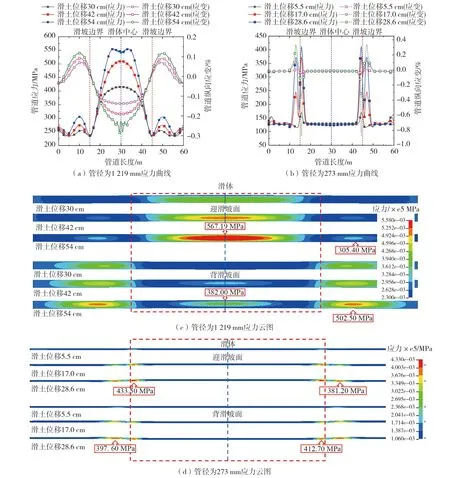
图3 不同滑土位移下管道应力曲线及其云图Fig. 3 Stress curves and nephogram of pipelines under different sliding-soil displacements

由图3(c)可知,当管径为1219 mm时,相比于背滑坡面,其应力极值出现在迎滑坡面滑体中心截面处,且随着管-土相互作用的增强,应力集中区域明显增大,且伴随着沿Z轴发生扭转现象;此时管道应力极值为567.19 MPa,超过其屈服强度,而纵向应变极值为0.36%,仍满足安全要求。针对于背滑坡面,主要承受滑坡前缘土体的阻碍作用,因而产生的应力较小;同时由于周界处固土端的阻碍,致其迎/背滑坡面在距周界一定范围内均出现较为显著的应力变化,且背滑面处应力值更大,其位置位于距滑坡周界约5 m处。由图3(d)可知,当管径为273 mm时,其应力极值点均位于滑体区域,当滑土位移为28.6 cm时,迎滑面应力极值为433.50 MPa,较之背滑面增长了4.80%,均已超过屈服强度,而此刻管道纵向应变极值为1.15%,且随着滑坡进一步演变,其应变值将超过临界值,应采取抗滑措施。

2 敷设于滑体内管道力学分析

2.1 敷设位置

为分析管道敷设位置所带来的影响,分别在滑体前缘、中部及后缘位置布置输气管道,管径选取φ1219 mm×22 mm,埋深均为1.2 m,且不同敷设位置处管道间距为5 m,其模型相关尺寸如图4所示。

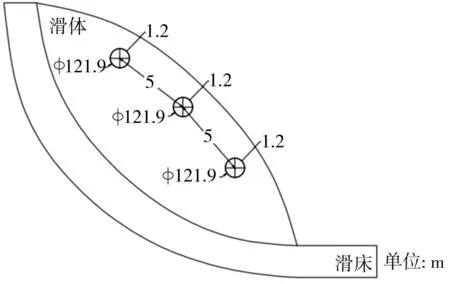
图4 滑体内管道敷设位置示意图Fig. 4 Schematic diagram of pipelines laying position in slide mass

由图5可知,当管道敷设于滑体不同位置时,在管土相互作用下,管道整体形变仍为“鞍”状;针对推移式滑坡,当管道位于滑体前缘时,所产生的位移量较小,其次为中部,后缘处管道产生位移量最大;当滑土位移为50 cm时,敷设于后缘处管道位移极值为76.70 cm,相比于中部、前缘位置处位移量增长了28.85%、62.65%;同理当滑土位移为90 cm时,后缘处管道位移极值为105.58 cm,同比增长16.14%、50.81%,相比于滑土位移为50 cm时,位移量差值有所降低,说明随滑坡逐渐演变,后缘土体逐渐推动前缘土体滑动,致使滑体中部及前缘处管道管土作用增强,管道位移量进一步增大。

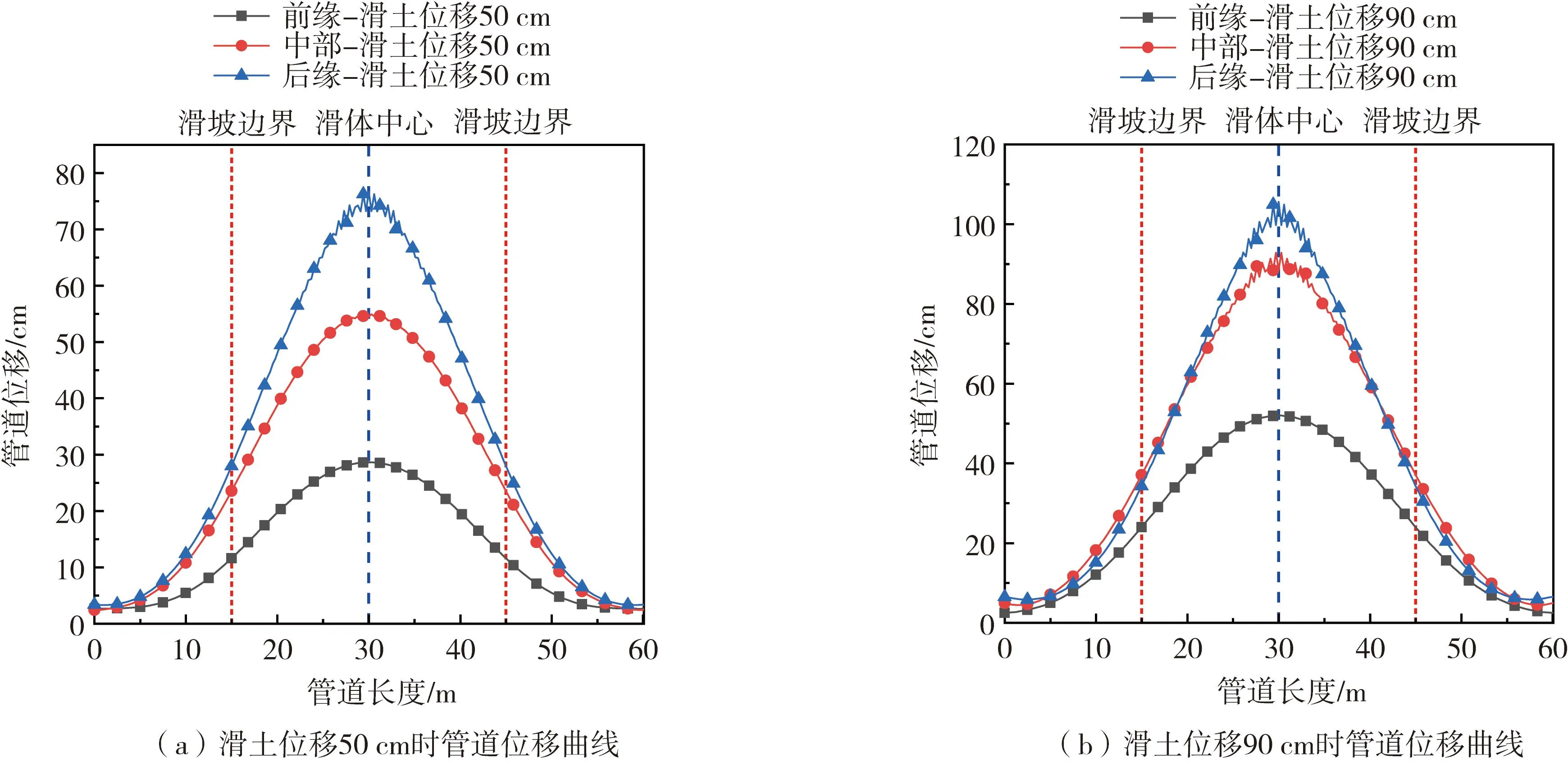
图5 不同敷设位置下管道位移曲线Fig. 5 Displacement curves of pipelines at different laying positions

由图6可知,针对于管道迎滑面,在滑土冲击作用下,处于滑体区域内的管道呈现压缩状态,产生压应力,当滑土位移为90 cm时,滑体前缘处管道压应力最大,其极值约为356.04 MPa,次之为滑体中部,滑体后缘处管道压应力最小。而对于周界两侧未滑区域,由于固土的阻碍作用,致使管体呈现拉伸状态,产生拉应力,且随着滑坡演变,其应力最大值向周界处移动,当滑土位移为90 cm时,其极值约为473.14 MPa,位于滑体前缘处管道拉应力值最小。

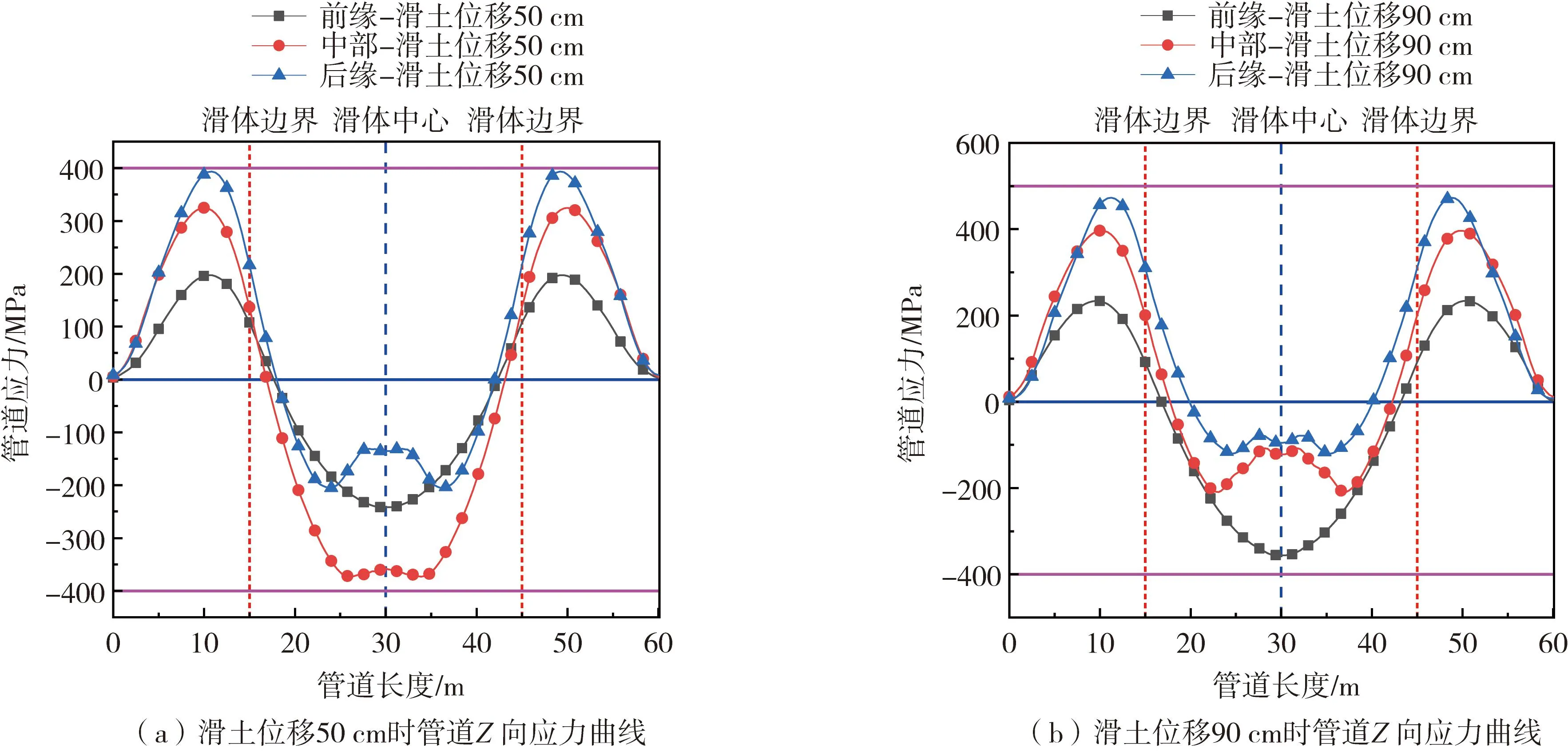
图6 不同敷设位置下管道Z向应力曲线Fig. 6 Z-stress curves of pipelines at different laying positions

2.2 管道埋深

以管道敷设于滑体前缘为研究对象,分别选取管道埋深为1.2、1.8、2.4 m,分析其埋深所带来的影响。由图7可知,当埋深为1.2 m时,在滑土下滑力作用下,管道所产生的位移及应力值较小,其值分别为28.65 cm、441.29 MPa;而当管道埋深为1.8、2.4 m时,其位移、应力曲线较为贴近,此时均小于屈服强度,处于安全状态。

图7 不同埋深下管道位移、应力曲线Fig. 7 Displacement and stress curves of pipelines at different buried depths

由图8可知,在管土相互作用下,不同滑土位移下管道所产生的屈服应变曲线走势大体相同,即当管道埋深为1.8 m时,所产生的屈服应变最大,减少或继续增大埋深可使其屈服应变适量减少,但此刻已进入塑性状态,需做好土体开挖释放应力或设置抗滑措施以保证管道的运行安全。

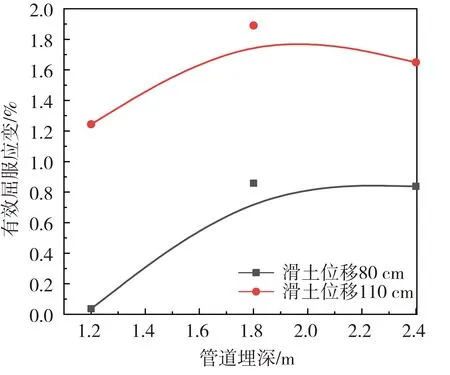
图8 不同埋深下管道屈服应变曲线Fig. 8 Yield strain curves of pipelines at different buried depths

2.3 管道壁厚

以管道敷设于滑体前缘为研究对象,分别选取壁厚为22.0、27.5、33.0 mm,分析管道壁厚所带来的影响。由图9(a)可知,随管土作用增强,不同壁厚下管道位移量均呈现增长趋势,但随着管道壁厚的增大,位移增量减小;同时,当滑土位移量小于60 cm时,其位移曲线基本重合,随管土作用进一步增强,管道位移以不同速率进行增长,说明滑坡演变过程中,位于前缘处管道只受其周围一定范围土体影响,管土作用较弱,进而壁厚的增加对管道位移量带来的影响甚微。由图9(b)可知,在滑土下滑力作用下,管道迎/背滑面均存在较为明显的应力集中区域,其截面应力曲线具有较好的对称性;当管道壁厚为22.0 mm时,其应力极值为555.51 MPa,已进入屈服状态,相比于壁厚为27.5、33.0 mm增大了12.06%、24.01%,此刻均未超过其屈服强度,即壁厚的增加,致使管道产生的应力值降低。

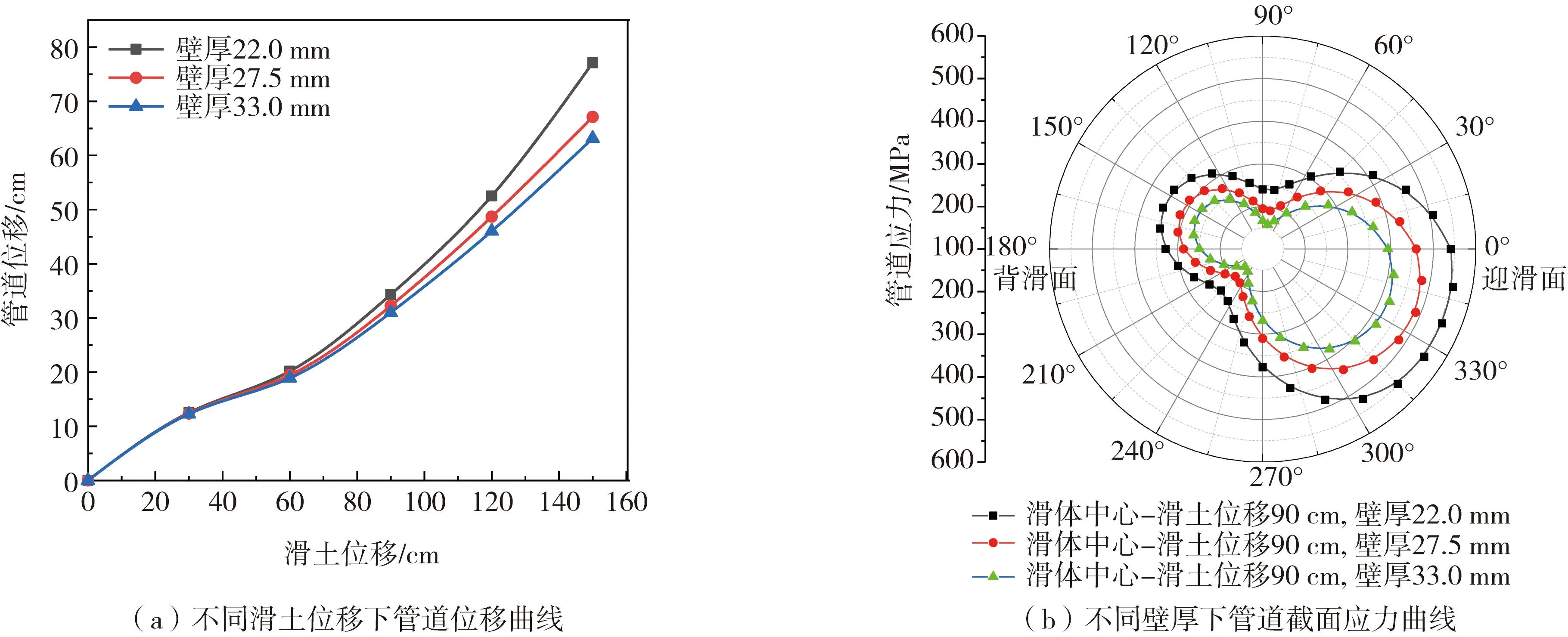
图9 管道位移及截面应力曲线Fig. 9 Displacement and stress curves of pipelines

3 敷设于滑体外管道力学分析

3.1 敷设位置

在管道敷设初期,为节约施工成本,保证管道后期运维安全,常常在设计阶段选线过程中避开地形地貌复杂、地质灾害频发地带。为分析敷设于滑体外管道受力情况,分别建立敷设于滑坡前部及后部管道模型,其埋深均为1.2 m,且与滑体距离均为3 m。

选取管道3点、9点方向路径,获取管道沿线应力数据。由图10可知,当管道敷设于滑体外部时,无论布置于滑坡前部还是后部,其应力值均未超过其屈服强度,满足管道的运输安全;当管道敷设于滑坡前部时,3点方向应力更大,且应力极值位于靠近周界处的滑体区域内;当管道敷设于滑坡后部时,同样3点方向应力较大,但其应力极值点位于滑体中心处,其值为339.78 MPa,较之敷设于前部管道应力值降低了15.74%。

图10 敷设于滑体外不同位置管道应力曲线Fig. 10 Stress curves of pipelines laid at different positions outside the sliding mass

由图11可知,针对于滑体中心处管道截面,敷设于滑体后部管道所产生的应力极值为424.35 MPa,位于158°处,而滑体前部管道应力值较小,降低了34.95%,位于78°处,且截面应力较为稳定,约为260 MPa;针对于滑体周界处管道截面,敷设于滑体前部管道应力较大,其应力极值为396.59 MPa,位于101°处,较后部管道应力增长了21.03%;综合对比应力数据发现,当管道敷设于滑体前部时,管道所产生的应力值更小,更为安全。

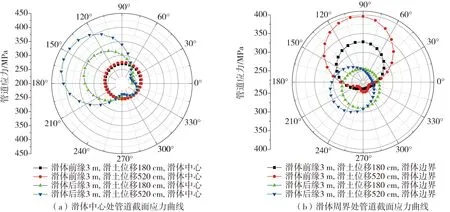
图11 敷设于滑体外管道不同截面应力曲线Fig. 11 Stress curves of different sections of pipelines laid outside the sliding mass

3.2 管道埋深与壁厚

同时以管道敷设于滑坡前部为对象,分别考虑其埋深及壁厚带来的影响,选取埋深为1.2、1.8、2.4 m,壁厚为22.0、27.5、33.0 mm,建立5种不同工况滑坡模型,获取不同滑土位移下管道应力、应变极值数据,并基于应力、应变准则对其进行评判,其相关数据如表3所示。由表3可知,当管道壁厚为22.0 mm,增加其埋深时,不同滑土位移下管道所产生的应力、应变极值基本稳定,埋深增加所带来的增益并不明显。其原因可能在于当管道敷设于滑坡外部时,管土耦合作用由滑土的冲击载荷转变为占压载荷,并通过管周稳定土体加以传递,此时管道安全与否更大程度取决于管周占压土体量;同时由于文中工况为推移式滑坡,前缘土体受限于后缘土体推动而发生滑动,即在特定滑坡规模下,随滑坡演变,后缘滑土下滑力减弱,滑体逐渐趋于稳定,而前缘临空,最终管顶覆土厚度约6.5 m,占压土体量较小,因而埋深的变化所带来的影响较小。当壁厚为33.0 mm,滑土位移630 cm时,其应力极值相比于壁厚22.0、27.5 mm减少了27.64%、4.32%,可见当管道穿越滑坡影响区时,提高壁厚可增强其可靠性;当壁厚为27.5 mm,继续增加壁厚时,其管道产生的纵向应变极值趋于稳定。

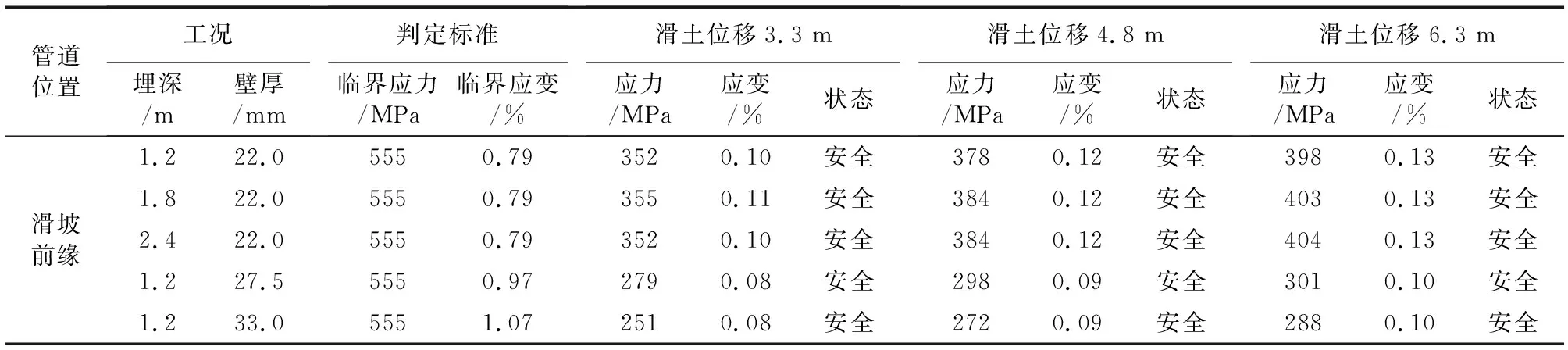
表3 不同工况下管道应力情况Table 3 Stress of pipelines under different working conditions

4 结论

基于SPH-FEM耦合方法,建立了土质滑坡下输气管道力学分析模型,并从设计角度出发,考虑管道敷设位置、埋深及壁厚等因素影响,辅以应力、应变准则加以判定,所得结论如下:

1)针对于横坡敷设管道,在管土互馈作用下,管道位移极值位于滑体中心处,整体呈现“鞍”状,且在滑坡周界处位移明显,致使表土“隆起”;当管径较大时,由于较大的管土接触面积,致使管道应力极值位于滑体中心;当管径较小时,呈现出不同的应力状态,即滑体周界两侧存在明显应力集中区域,而靠近滑体中心处应力值趋于稳定,易发生剪切破坏;同时相比于应变设计准则,应力设计准则更为保守,不能充分发挥管材性能。因此,为保证滑体区管道后期运维安全,应在管道中心、滑体周界及距周界一定距离固土端设置位移、应变等监测设备,以掌握滑体区管道受力情况。

2)针对于推移式滑坡,当管道敷设于滑体前缘时,其应力值、位移量较小,其次为滑体中部,而管道敷设于后缘时,更易过早进入屈服阶段;增大管道壁厚时,其承载能力得以提升;而对于埋深的增加,管道有效屈服应变呈现先增加而后减小的趋势。因此,当管道因敷设空间受限而不可避免地横穿推移式滑体区时,在保证管前土体稳定情况下,在其后缘进行土体削方或布置锚索抗滑桩、挡墙等抗滑措施,进而确保滑体稳定情况下,可优选布置在滑体前缘。

3)针对于推移式滑坡,且管道敷设于滑体外,当位于滑坡前部时,在滑体周界附近出现应力集中区域,而滑体中心管道截面应力较为稳定,而在后部时,则呈现相反状态,且应力极值更大,但2种敷设工况均未超过其应力、应变临界值,满足运行安全。因此,在现场条件允许情况下,应尽量优选管道敷设于滑坡前缘,且为保证管道安全,可在施工成本可控范围内适当增加管道壁厚,以减小应力。