基于高斯数据增广的小样本数据无人机编队类型抗扰识别

马琳琪，李校男，晁 涛，及鹏飞

（1. 哈尔滨工业大学控制与仿真中心，哈尔滨 150080；2. 四川腾盾科技有限公司，成都 610036）

1 引 言

无人机作为一种飞行器，可以在遥控或者自主控制下完成复杂飞行任务，近年来在军事领域越来越多地被应用［1-2］。但由于单架无人机受到探测能力、武器运载能力等多项因素的限制，在任务难度高、任务范围广的情况下不具有优势，因此出现了无人机群协同合作的作战模式，这些无人机群通过编队组织分工，可以完成战场侦察、突防攻击、火力支援等复杂任务［2］。随着无人机在军事作战中的作用增强，如何监测敌方无人机并有效预警的相关研究逐渐开展，其中包括无人机集群的编队类型识别。无人机集群通过调整队形，可以完成不同的作战任务，因此通过识别无人机集群的不同队形，可以有效对来袭敌机进行预警预测，辅助指挥部门进行战术决策。在军事领域中常见的无人机队形有楔形、菱形、纵形等，无人机采用菱形编队可将保护对象围在中间完成护送任务，采用纵队可对目标进行地毯式打击［1］，因此无人机编队类型的识别问题对于判断敌方意图并根据预测的意图来为我方及时作出预警至关重要。

编队类型识别问题从本质上来说是一种分类问题，通常采用基于模板匹配［3-4］或是机器学习的识别方法［5-7］，模板匹配例如基于空间方向相似性［8］、基于领域知识［9］等，这些方法通常只针对一些具体的队形模板，其队形描述的方式固定，不适用于无人机坐标数据观测不完全和含有杂波等干扰因素较多的情况，缺乏通用性。而基于机器学习的目标识别方法中，具有代表性的有基于BP（Back Propagation）神经网络［10］、支持向量机SVM（Support Vector Machine）［11］、循环神经网络RNN（Recurrent Neural Network）［12］等的目标识别算法，目前已有研究验证了这些方法在无人机编队识别问题中的有效性，但此类方法依赖大量的数据进行建模，对于小样本情形下的编队识别存在局限性。基于结合Hough 变换和K-means 聚类算法的队形识别算法本质上也是一种模板匹配算法，这种方法可以通过提取编队轮廓特征的方式将编队类型与轮廓参数相匹配，虽然同其他的模板匹配方法一样也需要建立模板库，但该算法特征提取的步骤简洁，相应特征的数据维度较小，并且可以在一定程度上过滤掉杂波等干扰因素的影响，同时相比于机器学习算法而言并不依赖于数据进行建模，因此该算法有着一定的优越性。

另外，无人机样本量少本质上是目标分类领域的小样本问题，针对小样本问题现在常见的处理方式有两种类型，一种是针对数据进行的数据增强（例如数据裁剪、翻转、添加噪声或是采用生成对抗网络进行数据生成等），另一种是针对模型进行模型优化（例如迁移学习、多任务学习、元学习等），这些方法均可以对小样本引起的模型鲁棒性等问题进行改善。

本文旨在结合Hough 变换和K-means 聚类算法，对含有噪声的无人机队列进行类型识别。针对无人机数目较少影响参数空间交点求解与聚类效果的问题，提出了一种基于高斯模型的原始数据增广方法，将原始数据与生成的虚拟数据融合，以提高聚类算法的精度及鲁棒性。将这些图形空间中的无人机坐标点数据通过Hough 变换映射为参数空间中的正弦曲线，统计这些正弦曲线的交点，去除重叠交点数较少的数据点，将剩余交点进行K-means 聚类，用聚类后的交点即可得到原图像空间中直线的参数。

本文首先介绍了Hough 变换和K-means 聚类算法的基本原理。然后，通过分析含杂波小样本队列信息带来的问题，详细介绍了编队类型抗扰识别算法流程。最后，以常见的菱形队列为例，通过计算机仿真对算法的有效性进行了分析。

2 Hough变换原理

Hough 变换［13］由Paul Hough 提出，它的基本原理是利用图像空间和Hough 参数空间的点-线对偶性，将图像空间中的检测问题转换至参数空间中进行。以直角坐标系为例，在直角坐标系中的直线，其斜率-截距表达式如式（1），式（1）可等价变换为式（2）。

将x，y视为参数，k和b视为自变量，则x-y平面中的每一个点都对应k-b平面中的一条直线，因此，x-y平面中同一条直线上的点可以转换成kb平面中的多条直线，这些直线的交点即可确定xy平面中这条直线的参数［4］。

这种基于斜率-截距表达式的Hough 变换，对于垂直于x轴的直线很难进行表达，因此Dude等［13］将极坐标引入，把直角坐标系中的数据转换到极坐标系表示。直线L的极坐标表达式为

式中，ρ表示图像空间中原点到直线的垂线段的长度，而θ表示这条垂线与极坐标中极轴的夹角。若将x，y看作是参数，对应地将ρ和θ看作是自变量，那么直线L上的任意一点都可以转变成极坐标系下的一条正弦曲线，如图1 所示。这些参数空间中的正弦曲线交于一点，这一点对应的ρ和θ即可确定直线L的表达式。

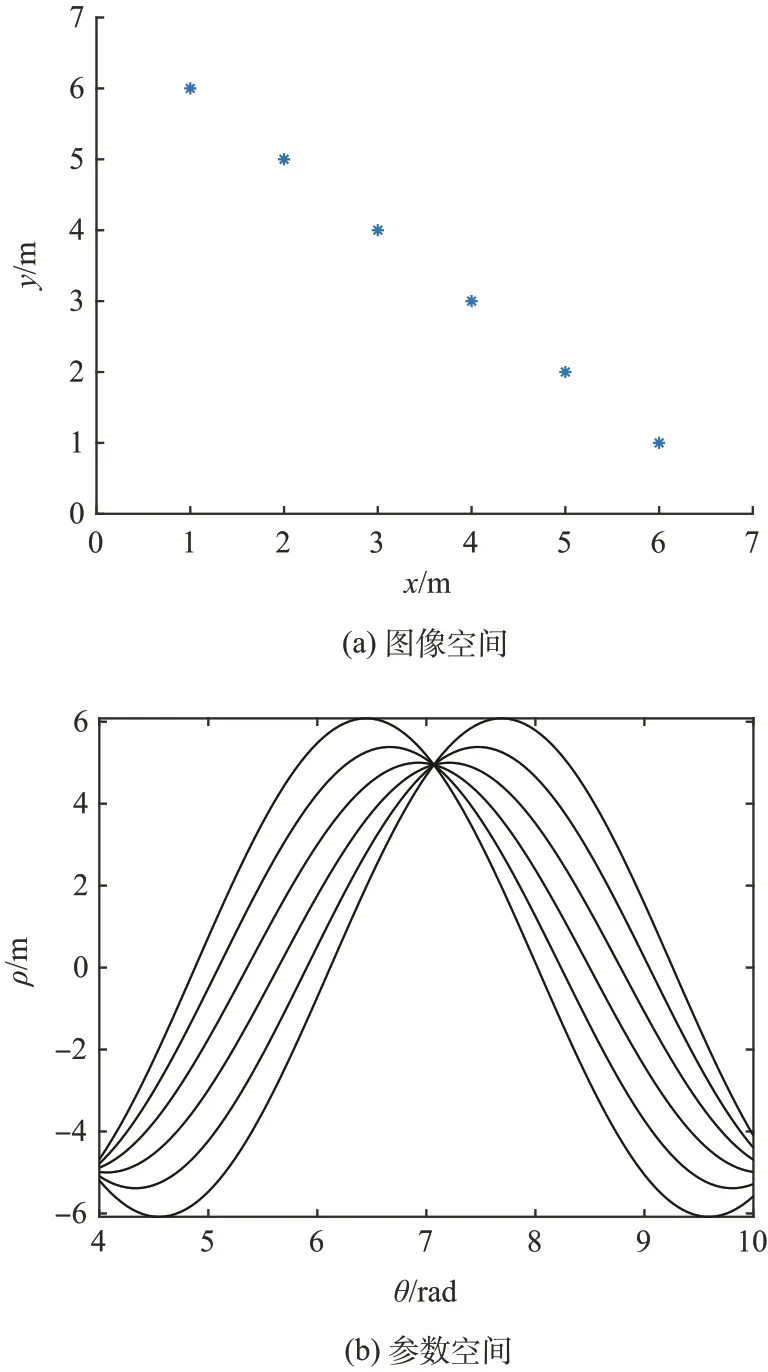
图1 直线样本及其Hough变换后曲线Fig.1 Straight line samples and their Hough transformed curves

3 K-means聚类算法原理

K-means［14］为最常用的基于欧氏距离的聚类算法，该算法的使用基于一个基本前提，那就是如果两个目标在欧氏距离度量下的距离越小，那么他们的相似度就越大。本文对提取到的候选交点使用K-means 聚类得到类中心，以类中心作为最终选择的直线参数，下面是算法的详细介绍。

K-means 算法大致分为三步，第一步初始化类中心，第二步将数据点分配给最近的类中心，第三步更新类中心。其中第二步和第三步迭代进行，直到最后类中心稳定收敛。

针对第一步类中心的选择，可以随机选择k个数据点，也可使用Lloyd［15］、K-means++［16］、SKMeans++［17］等方法动态选择。经过综合比较，本文最终使用K-means++选择初始化k个类中心。

4 无人机编队类型抗扰识别算法

本章将详细介绍本文提出的基于高斯模型增广原始数据的无人机编队类型抗扰识别算法。首先分析了当样本数据较少，且含有噪声干扰时，直接使用Hough 变换会带来的问题。进而提出使用高斯模型对原始数据进行增广，以获得更好的交点提取与聚类效果。

本章以菱形队列为例，详细阐述了使用Hough变换，K-means 聚类进行队形轮廓提取的方法。在该方法中将无人机编队中的单个无人机视作一个坐标点，根据无人机群中各个无人机的相对位置将其抽象为一个点集，每个点由一个横纵坐标表示，然后以该点集作为识别算法的输入数据，在菱形编队示例中，该编队的16 架无人机对应着二维平面中的16 个坐标点，如图2 所示，算法的具体流程如图3所示。

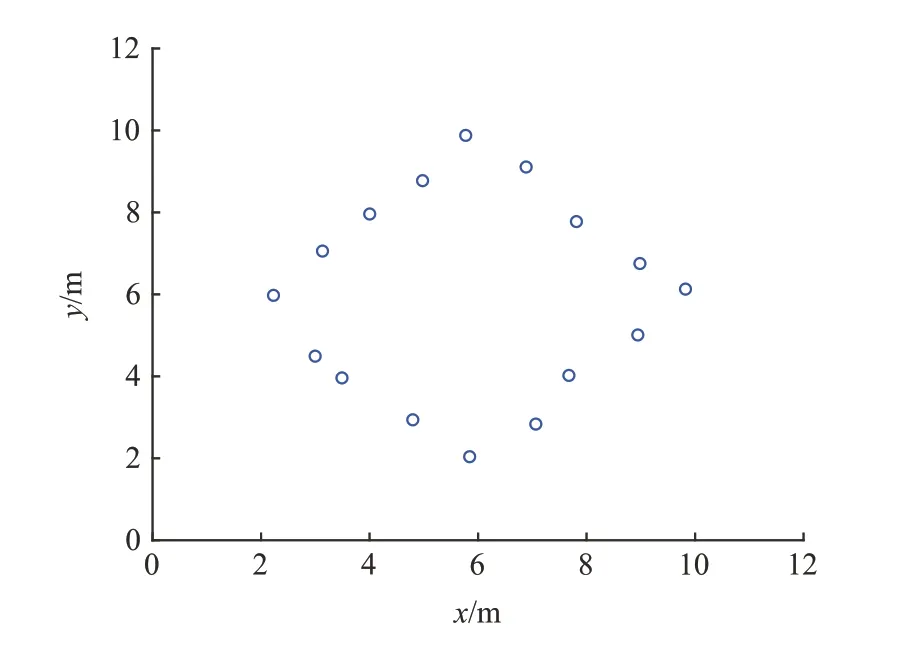
图2 带扰动的菱形队形数据Fig.2 Perturbed diamond formation data

在实际应用中，可以通过雷达等观测设备获得无人机群的位置信息，再对获得的观测数据按照上述逻辑进行转换，从而应用该识别算法进行编队类型的识别。

4.1 基于高斯模型的数据增广

在实际应用过程中，即使无人机保持直线编队行进，受采集设备精度及噪声影响，采集到的数据点也无法完美分布在同一直线上，这将导致参数空间中的曲线无法相交于一个点［18］，如图4所示。

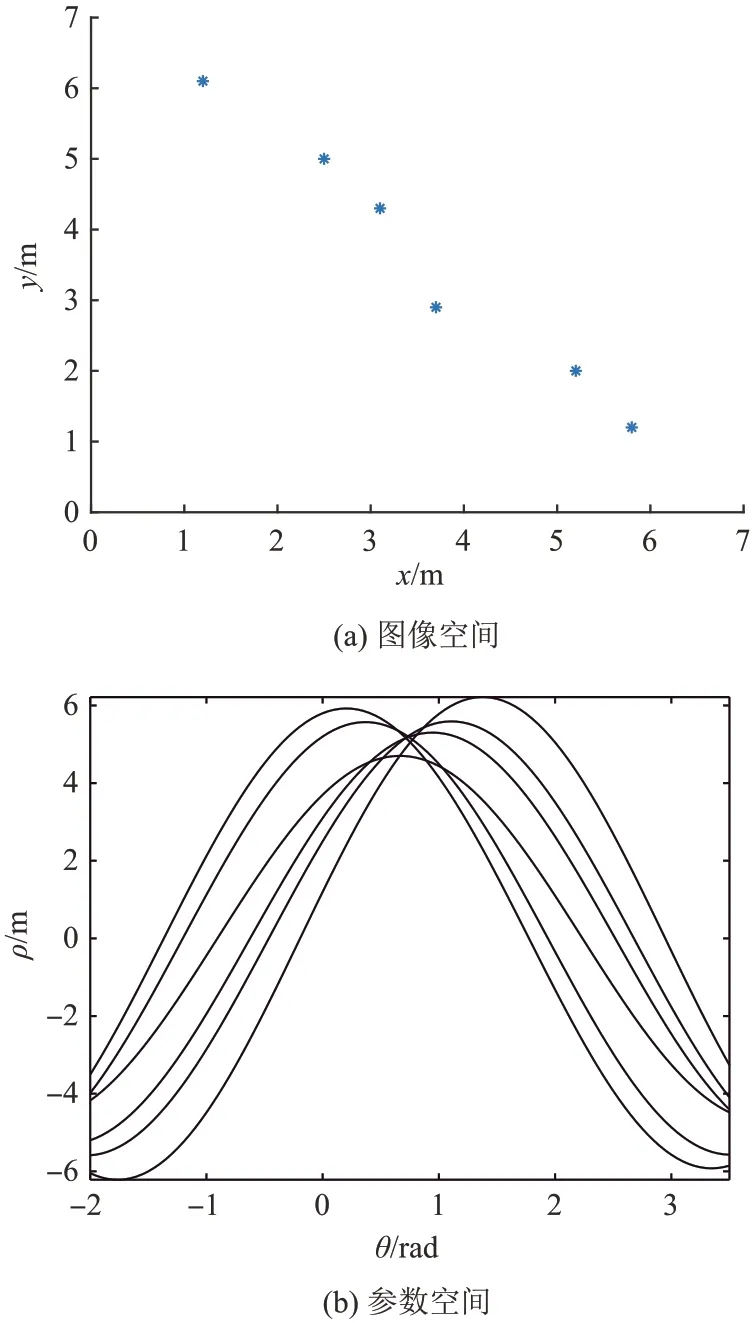
图4 带扰动的直线样本及其Hough变换后曲线Fig.4 The perturbed straight line sample and its Hough transformed curve

与图1相比，图4在原始图像空间中的点不再完美符合直线分布，这样一来，在参数空间中的曲线会相交于多个点。相交的点数增加无疑为问题的求解带来了难度，需要求解的交点数增加，求得交点后如何选择或融合为合适的一个点成为一个新的问题。

针对以上问题，已有前人的研究［4，19］选择使用聚类算法来获得最终的解，通过提取相交曲线数大于一定阈值的候选点，对候选点进行聚类，以最终的类中心作为结果。这样的方法取得了不错的效果。但由于在小样本无人机编队类型识别中，无人机的数目较少，可获得的候选交点也会较少，聚类数据的不足无疑会严重影响聚类算法的准确性。因此本文提出了使用高斯模型在一定的小范围内增广原始数据，将原始数据与生成的虚拟数据一同进行Hough 变换与聚类，有效地增加了参数空间中的候选交点数，为聚类算法提供了更加充足的数据，能够获得更好的聚类效果。具体方法是将原始数据点视作一个高斯分布，而非独立的点，则可以一定的方差σ，按照式（4）所示二维高斯概率分布来生成虚拟数据。

式中，(μ1，μ2)对应原始数据中的点(x，y)，σ1与σ2为高斯分布中的标准差，为不失一般性，在本文中使用σ=σ1=σ2。图5 即为对原始数据中每个点使用σ= 0.2 的二维高斯分布生成10 个虚拟数据点后的结果。

图5 高斯增广后数据分布Fig.5 Gaussian augmented data distribution

4.2 Hough变换与交点统计

得到增广的数据后，对其使用Hough 变换即可得到参数空间的正弦曲线。为直观展示数据增广为交点选取带来的有利影响，图6 给出了原始数据和增广后数据的参数空间曲线。

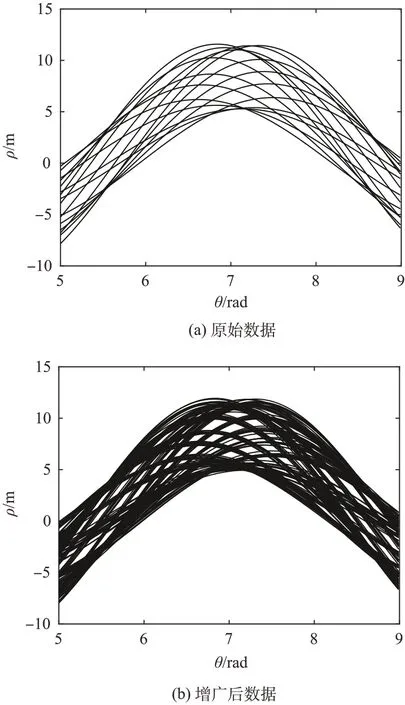
图6 增广后的样本及其Hough变换后曲线Fig.6 Augmented samples and their Hough transformed curves

从图中可以看出，使用高斯分布对原始数据进行增广后，参数空间中的线条数增多，对应的交点数也明显增加，这将大大提高算法对原始数据中噪声的鲁棒性。

由于使用计算机对曲线进行处理的过程中，直接在参数空间中通过曲线的解析式来获得交点的解析解计算成本过高，可实施性不强，所以需要恰当的离散化手段对参数空间曲线进行离散化处理，然后根据离散化的结果，统计相交于同一点的曲线数，根据统计的重叠交点分布设定合适阈值获得最后用于聚类的候选交点。离散化间隔如果选取过大，则在同一个离散网格内会囊括过多的点，甚至会包含进一些错误的交点；间隔若选取过小，则容易导致落在同一离散网格内的点过少而错过最优交点，所以合适的离散化间隔选择将尤为重要，如图7 所示，即为选取Δθ为0.1 rad，Δρ为0.1 m时统计的重叠交点数分布图。

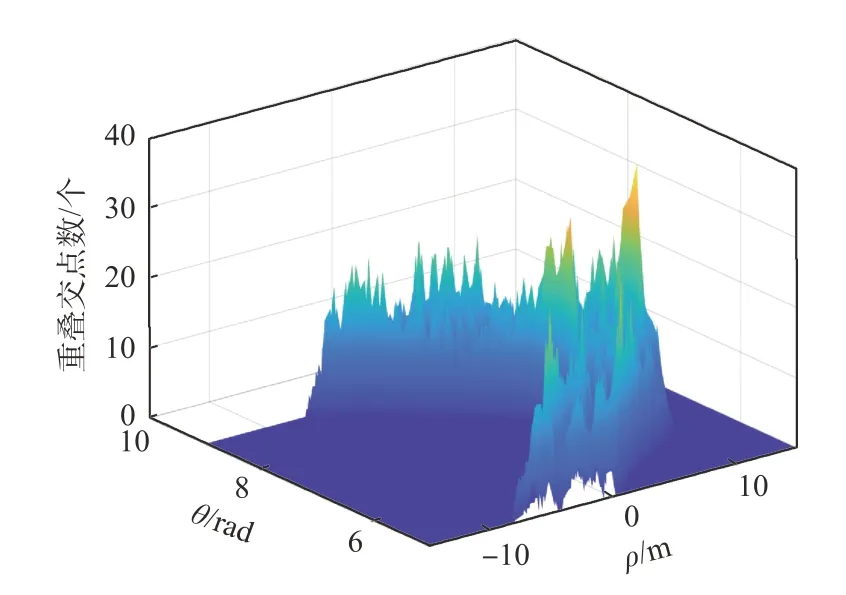
图7 重叠交点分布图Fig.7 Overlapping intersection plots

统计出重叠交点数分布后，通过选择合适的阈值提取出峰值点，提取出的峰值点将作为聚类的候选交点。重叠交点数的提取依赖合适的阈值，阈值选取过大会造成数据丢失，选取过小则会放大杂波干扰，影响后续的聚类效果，所以合适的阈值选择也尤为重要，峰值点提取出来后便可以进一步聚类分析［20］。

4.3 交点聚类与队形轮廓提取

得到提取出的峰值点后，应用K-means++进行初始类中心的选取，接着使用通用K-means 算法进行聚类，在参数空间中获得期望的类中心，具体步骤如下：

（1）首先从候选交点数据集X={(θi，ρi)，i=1，2，3...N}中随机均匀选择一个数据，将此数据点作为第一个初始类中心，记为c1。

（2）计算从每个数据点到已选择类中心（初始时仅有c1）的距离。将cj和各个数据点xm之间的欧几里得距离表示为d(xm，cj)。

（3）在数据集X中选择余下的类中心，选择的概率遵循

式中，Cp表示最接近cp的所有数据点的集合，即每次选择类中心时，其被选择概率与它到已选最近中心的距离成负相关。

（4）迭代步骤（3），直到选择到了k个类中心。

使用K-means++选择到k个类中心后，就可以在数据中迭代更新类中心直至最后收敛，具体步骤如（5）～（7）。

（5）计算所有数据点到每个类中心的欧几里得距离，将每个数据点分配给离其最近的类中心，即对每一个样本xp，将会按照式（6）分配给集合S(t)：

式中，t代表迭代次数。

（6）计算每个簇S(t)中数据点的平均值，将此平均值作为新的k个类中心，

（7）迭代进行（5）、（6）步骤，直到最终的类中心不再改变。

至此，提取出的峰值点通过K-means 聚类算法提取出各个簇的类中心，将参数代回式（3）即可获得在原始图像空间取出的直线，如图8所示。

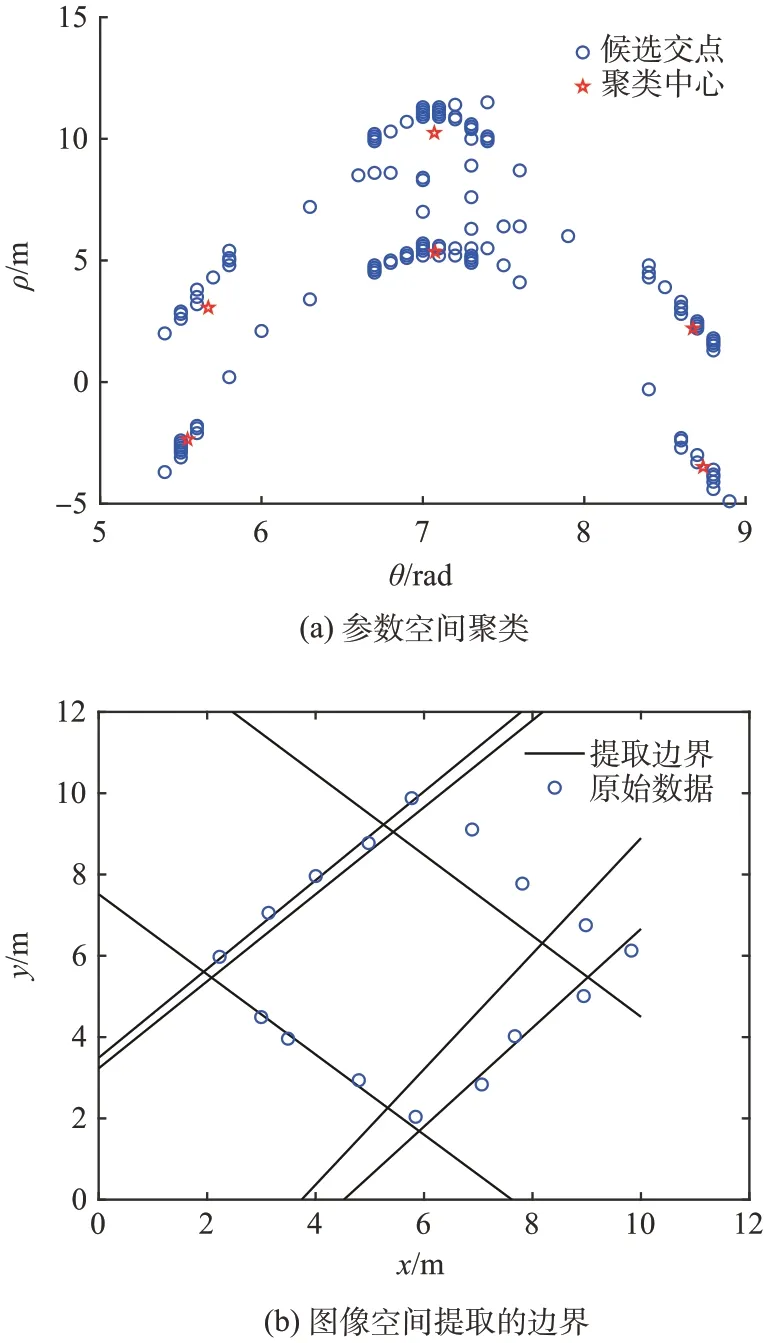
图8 高斯增广后数据点的聚类与边界提取Fig.8 Clustering and boundary extraction of data points after Gaussian augmentation

可以注意到，虽然菱形只有四条直线，但提取出的类中心是6个，对应着6条直线。这是因为正弦函数具有周期性，所以在选取计算的窗口中可能存在多于期望直线数的交点。但这些周期性的点映射回原图像空间后会重叠，经过适当的滤波后便能融合在一起。获得提取到的队形轮廓后，使用模板匹配或神经网络等方法即可获得编队类型识别结果。

5 仿真结果与分析

本文聚焦于无人机队形识别，在常见的无人机队形中选取了较为复杂的菱形队列，通过生成含有噪声的菱形无人机队列数据来评估所提方法对编队类型的识别性能。直接对原始数据使用识别算法与在高斯增广后对数据使用抗扰识别算法的仿真结果对比如图9所示。

图9 原始数据与使用增广数据仿真结果对比Fig.9 Comparison of original data and simulation results using augmented data

从实验结果可以看到，在使用基于高斯模型的增广数据后，可用于聚类的候选交点数目明显增加，由此也获得了更好的聚类效果。从最后映射回图像空间的结果来看，使用增广数据后提取的直线也更加准确。直接在原始数据上提取虽然提取到了正确的边界，但还提取出了两条错误的直线（另一条由于偏移过大，没有显示在图9 选择展示的范围中）。这有力证明了使用基于高斯模型的增广数据后，算法的鲁棒性得到了显著提升。

为进一步探索基于高斯模型的增广数据对最终效果的影响，本文通过变化高斯模型中的标准差σ，探索不同σ对最终直线提取效果的影响。本文使用最终提取的队形边界直线的k，b参数与期望的标准直线的k，b参数的均方误差作为评估指标。均方误差越低，说明提取出的边界信息越准确，具体结果如表1所示。

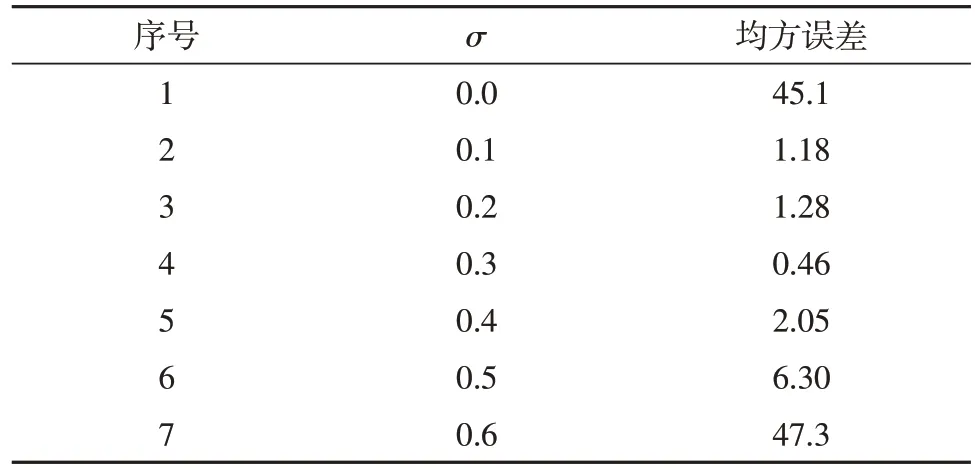
表1 使用不同σ得到边界参数的均方误差Table 1 Use different σto get the MSE of the boundary parameters

从表中可以看出，在使用了基于高斯模型的增广数据后，模型提取出的队形边界更为准确，这是因为高斯分布的增广数据有效增加了参数空间中的交点数，使K-means 聚类算法表现得更加稳定。除此之外，由于原始数据量小，且存在噪声，加入额外高斯分布的数据能够有效缓解原始数据中噪声对识别算法带来的负面影响。

本文所采用的算法与前面提到的数据增强方法有一定的相似性，但又略有不同，在做法上都是添加一定的高斯噪声生成新的数据，前面提到的数据增强算法是直接生成高斯噪声纳入训练数据，而本文是将生成的高斯噪声围绕原始数据点展开，即以原始数据作为原点生成相应的噪声，这样能够更好地保留数据的特征。

从实验结果来看，基于高斯模型扩充原始数据后，使用Hough 和K-means 算法能够有效提取出无人机队形边界，这样一来再使用模板匹配或神经网络分类等方法就能轻松地识别无人机的编队类型。

通过可视化的方式对仿真结果进行更加直观的分析，如图10 所示，可以看到当标准差等于0.3 时识别结果的均方误差最小（0.46），以0.1的步长对标准差进行增大或者减小时，均方误差均会增大，并且当标准差小于0.1 或者大于0.5时，均方误差急剧增大，在0.1～0.5的范围内变化则较为平缓。

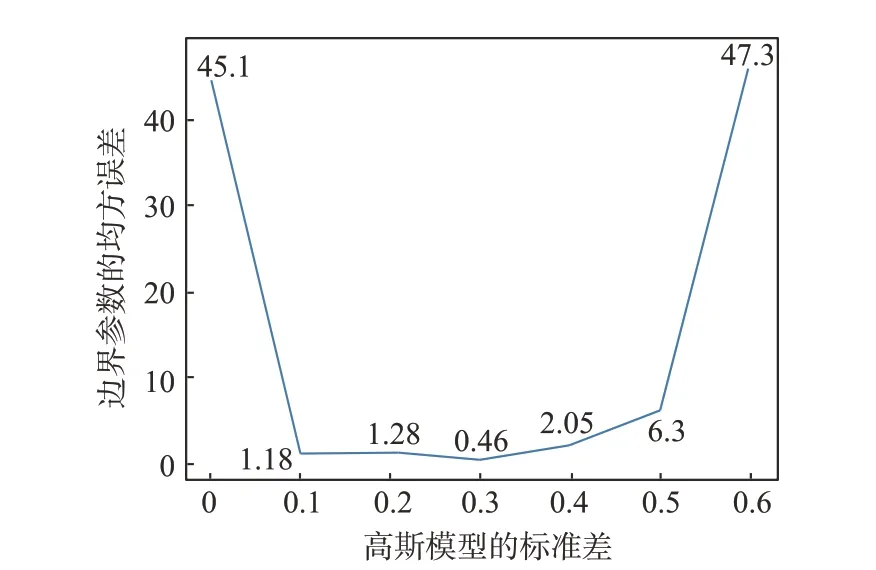
图10 边界参数的均方误差随高斯模型标准差的变化Fig.10 The variation of mean square error of boundary parameters with Gaussian model standard deviation

仿真结果中原始模型的均方误差高达45.1，而本文采用的方法可以将均方误差降低至0.46，证实了方法的有效性。

为了进一步证实本文提出的基于高斯数据增广的小样本数据无人机编队类型抗扰识别算法对多种常见无人机编队类型识别的有效性，设计带有噪声的纵行及楔形编队并使用该算法进行识别，其对应的待识别增广数据和图像空间边界提取如图11、图12所示。

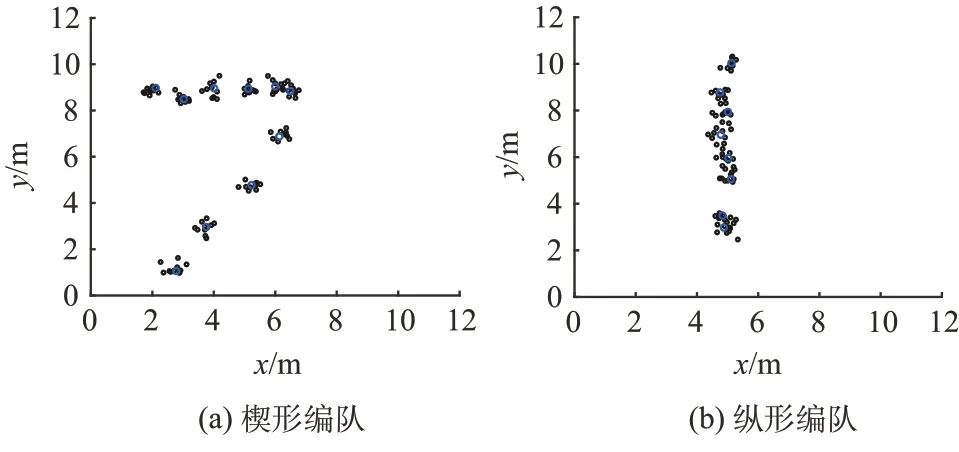
图11 待识别编队增广数据Fig.11 The formation to be identified

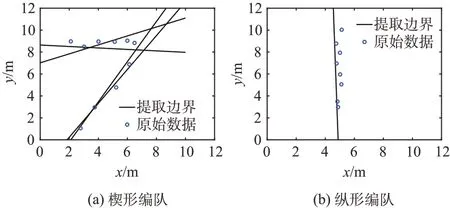
图12 图像空间提取的边界Fig.12 The boundary of image space

可以看到，本文提出的基于高斯数据增广的小样本数据无人机编队类型抗扰识别算法在菱形编队、楔形编队、纵行编队等常见编队类型的边界提取中均有着不错的效果，在此边界提取的基础上可以进一步地有效进行编队类型的判断。

本文提出的基于高斯模型增广原始数据的无人机机群特征聚类算法，将原始数据点视作一个高斯分布，而非独立的点，从而将编队中原始点扩充得到更丰富的候选点用于参数空间聚类，聚类得到的结果也更加趋近于真实值。这种方法的显著优点是对噪声或者缺失值有着相当好的鲁棒性，因为围绕每个原始点额外添加的数据点有效地抵消了噪声的影响，丰富了样本的特征。另外，相对于如文献［3］所用到的基于模板匹配的识别算法来说，本文的算法流程简化了特征提取步骤的繁杂计算，避免了针对队形规律的公式推导，从而提高了匹配并识别不同类型编队的灵活性；而相对于近期兴起的机器学习方法来说［5］，本文所采用的算法不依赖大规模数据集来训练网络，仅需要少量样本来建立模板库即可，很适合敌方无人机信息有限的应用场景。

6 结 论

本文创新性地提出了通过将无人机编队原始数据点视作一个高斯分布的方式对原始数据进行增广，在增广数据的基础上通过使用Hough 变换、离散化参数空间、统计重叠交点并提取聚类候选点、对候选点进行K-means 聚类的方法实现了对无人机队形轮廓的提取，并以带有噪声的菱形编队为例通过仿真实验验证了方法的有效性。其中，将原始数据中的每个点视作一个高斯分布的数据增广方式以及离散化参数空间以进行交点统计的交点计算方式均是本文的重点创新点，如前文所述，前者有效改善了候选点的聚类效果，提取出了更加准确的边界参数，后者则大大提高了交点统计的计算效率。文中也对应用该方法到工程场景中时的数据来源、数据处理方式进行了分析和说明。通过该方法提取出的无人机队形轮廓能够为编队类型识别提供良好的特征表示。

本文提出的使用高斯模型增广原始小样本数据的方式，为后续的聚类算法提供了更加丰富的样本，提高了聚类算法的鲁棒性，为之后的相关研究提供了很好的参考。在使用Hough 变换提取队形轮廓时，正弦函数带来的周期性重复点的去重问题还有待进一步研究。