基于势场导引的空地跨域协同探测方法

于汶江，谢旭东，王子凡，尹登宇，颜 鹏，郭继峰*

（1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 成都飞机设计研究所，成都 610031）

1 引 言

随着无人系统技术的快速发展，多无人系统集群的优势越来越显著。同时，面对任务场景的复杂化与多元化，同构无人系统在完成复杂任务时愈发捉襟见肘，而跨域异构无人系统可充分发挥不同空间域无人平台的优势，例如，在协同探测问题中，无人机平台具有飞行速度快、探测范围广的优势，但探测程度稍显不足；无人车平台探测程度高、运载能力强，但行进速度慢、探测范围窄。通过部署不同空间域的无人平台，能使无人系统不同领域的子成员优势互补，为高效完成更加复杂的体系任务提供了可能性［1］，拥有广阔的应用前景。目前，已有相关研究学者将跨域异构无人系统协同技术应用在灾难搜索救援［2］、目标搜索与打击［3］、海上反潜搜索［4］等民用与军事领域。

对未知区域的探测是无人系统的典型任务场景之一，对该问题的研究可扩展应用到诸多领域如地形勘察与测绘［5-7］、植物生长情况收集［8-10］、灾后人员搜救与受损评估［11-12］、星球探测［13-14］等，具有广泛的应用性。

在单空间域多平台协同探测方面已有大量的相关研究。余翔等针对应急救援过程中搜索问题提出了一种多无人机协同覆盖搜索算法，通过聚类算法进行任务分割，并引入A*算法进行求解［15］。过劲劲等针对四旋翼集群协同搜索，以信息素来引导多无人机进行两次搜索，通过滚动优化来达到快速搜索的效果［16］。

在跨域异构无人系统协同探测方面，梁月乾等针对跨域异构无人集群任务规划问题，建立了混合整数线性规划模型，以最小化任务时间为目标，通过分支界定法求解得到任务规划的最优方案［17］。李明龙等面向地震场景提出了一种协同搜索框架，通过拍卖任务规划方法对无人机群体进行任务规划，通过对遗传算法的改进提出了针对救援无人车的任务规划［18］。Wu 等针对城市环境引入无人机与地面无人车辆系统，分别为其生成环形路径来优化其任务时间，实现全覆盖路径规划［19］。Ni 等针对无人机与无人车组成的异构无人系统，基于网格方法并结合生物启发神经网络，引入蜻蜓算法，实现实时路径规划［20］。

以上研究人员所提出的算法能良好地执行特定任务，然而当任务环境迁移到跨域协同探测时却困难重重，无法很好地完成探测任务。同时，现实情况中，无人机与无人车只进行一次覆盖扫描探测时，往往无法达到所要求的探测程度，例如，在矿物质勘探过程中，将矿物质勘测程度视为探测程度，即该区域矿物质勘测程度越高，则该区域探测程度越高。然而无人机或无人车对该区域仅进行一次探测时，通常无法一次性勘探出该区域所有的矿物质资源，且不同的无人平台探测能力有强有弱，导致区域内的单次覆盖探测无法达到任务所需的探测程度。多数研究在进行探测规划时往往忽略这一点，所设计算法通常以完成有限次数覆盖探测为任务结束标志［1-2，15-18］。综上，本文受人工势场法启发，创新性地提出了一种基于势场导引法的探测策略，能在较短的时间内以规定的探测程度要求完成对全部未知区域的探测任务。本文主要创新点如下：（1）受人工势场法启发，提出了一种通过设计地图势场来为不同无人平台提供导引以完成探测的方法；（2）该方法能够依据各无人平台探测能力的不同，进行多次区域覆盖探测以达到规定的探测程度；（3）该方法能够支持多种类多空间域异构无人平台进行协同探测。

本文章节安排如下：第一章为引言部分，阐述了跨域异构无人系统协同探测的优势及必要性，以及单空间域多无人平台协同探测、跨域异构无人系统协同探测的国内外研究现状，和本文的主要研究内容、创新点与文章结构；第二章为建模部分，分别构建了无人车与无人机各自的运动学模型、探测模型，并对文章拟解决的具体问题进行了建模及描述；第三章为探测方法部分，通过栅格化方法将地图进行离散，介绍了人工势场法模型的原理，在此基础上，从探测程度函数设计、势场导引函数设计、避障能力设计三部分阐述了本文所提出的势场导引法；第四章为数值试验部分，通过搭建合理的仿真试验，验证了文章所提方法的正确性及合理性，并通过与其他算法进行对比，验证了本文所提方法的优势。

2 协同探测问题建模

2.1 无人机模型

2.1.1 无人机运动学模型

该问题求解过程中，无人机被设定为以固定高度飞行，如图1（a）所示，因此，无人机的运动学模型可被简化为两个维度

图1 无人机模型图Fig.1 UAV model diagram

式中，(xi，yi)，(vxi，vyi)与分别表示无人机i在二维笛卡尔坐标系下的位置、速度和指令速度，τv为与无人机运动学相关的时间常数。无人机运动受最大速度限制，即|vi|≤vmax。

2.1.2 无人机探测模型

无人机的向下探测范围可等效为一个半径为r1的圆形，如图1（b）所示，当栅格中心落入圆形探测区域内，则代表该栅格被探测到。

2.2 无人车模型

2.2.1 无人车运动学模型

无人车可被简化为在二维平面内运动，如图2（a）所示，其运动学模型为

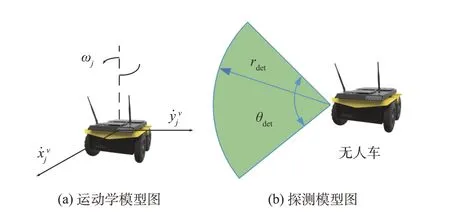
图2 无人车模型图Fig.2 UGV model diagram

2.2.2 无人车探测模型

无人车探测范围可简化为车前方一扇面角为θdet、半径为rdet的扇形，如图2（b）所示。当扇形探测面探测到地图栅格中心即可认为该栅格被探测到。

2.3 空地协同探测问题

本文针对空地跨域协同探测问题展开研究。给定未知区域后，要求多无人机与无人车对该区域进行协同探测，在最短时间内以规定的探测程度完成未知区域探索的同时不与周围障碍物及其他无人平台发生碰撞，场景示例如图3所示。

图3 任务场景示例图Fig.3 Task scene diagram

该问题数学表达式为

3 跨域协同探测方法

3.1 地图栅格化

本文将未知区域抽象为几何栅格区域，每个栅格可提供四种信息，分别为：

（1）该栅格是否为障碍物。

（2）该栅格与无人平台在位置区域投影面的欧几里得距离。

（3）该栅格中心与无人平台之间的连线与无人平台前进方向所形成的夹角。

（4）该栅格的探测度。当栅格中心点落入无人平台探测范围时被认为该栅格已被探测到，并更新该栅格探测度。

3.2 人工势场模型

传统人工势场模型仿照物理学中电场而建立，如图4 所示，目标点对无人平台产生的虚拟引力、障碍物及其他无人平台对无人平台的虚拟斥力，二者共同对无人平台产生合力，如图5 所示，导引无人平台能够不与障碍物及其他平台发生碰撞，并安全地抵达目标点。

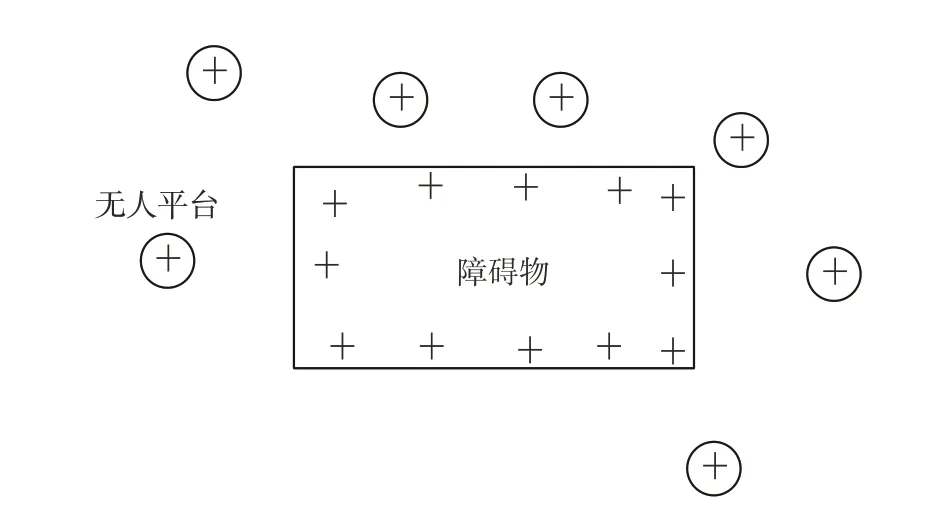
图4 势场示意图Fig.4 Potential field diagram

图5 二维平面受力分析Fig.5 Two-dimensional plane stress analysis

以单障碍物为例，无人平台所处势场定义为

设无人平台在区域内位置为(x，y)，则引力势场函数可表示为

式中，Uatt为机器人相对于目标的引力场，k为引力势场常量，X为无人平台位置坐标，Xg为目标位置坐标。

斥力势场函数可表示为

式中，Urep为平台所处的斥力场，η为斥力势场增益系数，ρ为平台与障碍物的最短欧几里得距离。ρ0为单个障碍物影响的最大距离，即若平台在障碍物影响距离之外不受障碍物斥力作用；反之，则受到障碍物的排斥作用。

对引力势场函数与斥力势场函数求负梯度，可得到相应力函数，则总势场对平台产生的合力为

3.3 基于改进人工势场的协同探测策略

本文所设计协同探测策略基本思想为：通过将未知区域地图栅格化以区分可行区域和障碍物。可行区域会对无人平台产生引力，引力大小受栅格探测程度及与无人平台的距离影响，无人机与无人车针对各自探测优势，通过权衡两种影响因素分别产生其在探测过程中的侧重点，进而生成不同的探测策略进行协同探测。障碍物对无人平台产生斥力，使得平台不会与障碍物发生碰撞。当无人平台对某栅格完成一次探测后，依据一定函数关系更新该栅格探测程度，从而影响对平台的吸引力，如此反复迭代，最终导引无人机与无人车协同完成整片未知区域的覆盖探测。因此，该探测策略共包括探测程度函数设计、势场导引函数设计与避障能力设计三个关键部分，详细阐述如下：

（1）探测程度函数设计

本文设计可行区域栅格的探测程度通过百分数量化表示，由0 到100%代表该栅格探测程度依次增高。然而，实际情况中，受各种限制因素影响，某一区域的探测程度几乎无法达到100%，因此本文规定当栅格探测程度达到所要求的最低探测程度Pmin时可认为该栅格探测完成。

无人平台移动过程中，定义栅格几何中心落入平台探测区域内即可视为完成一次探测，更新该栅格探测程度。且区域的探测程度随着次数增加往往不是线性增加，而应是一条增幅越来越小的曲线，对应实际情况中，一个区域的新情况往往更不易发现。因此设计栅格探测程度随探测次数变化函数为

式中，Pi(t)为t时刻栅格Pi的探测程度，k为无人平台探测能力的系数。

式（8）表明，某一时刻该栅格的探测程度受上一时刻探测程度与无人平台探测能力k共同影响，其中k无人车＞k无人机。随着Pi的增加，公式后一项数值越来越小，使得曲线增幅越来越小，符合实际情况。

绘制出探测程度随探测次数变化曲线如图6所示。在此给定k无人车= 0.65，k无人机= 0.45。

（2）势场导引函数设计

可行区域中，未完成探测的栅格对无人平台的吸引能力应与该栅格探测程度成负相关，即某一栅格探测程度越高，代表该栅格的探测优先度越低，对无人平台的吸引力越低，当该栅格探测完成后，失去对无人平台的吸引能力。然而无人平台探测过程中不能仅仅考虑栅格探测程度的影响，否则可能会导致某一栅格同时吸引所有平台，反而降低探测效率。因此设计势场导引函数时，需综合考虑栅格探测程度和该栅格与无人平台的距离，使得势场始终导引无人平台向着距自身最近且探测程度最低的栅格前进。

据此建立势场导引函数为

式中，Pij为地图中某一栅格的探测程度；dij为无人平台与该栅格中心的距离；k1、k2分别为栅格探测程度与距离因素导引无人平台的权重系数；Pmin为要求的栅格最低探测程度；min（P）为当前时刻地图中所有栅格的最低探测程度。

势场导引函数为无人系统赋予的协同性体现在：无人机飞行速度快，通过为其设置较高的k1与较低的k2可削弱距离对其产生的影响，使其侧重于优先探测地图中探测程度较低的栅格。无人车探测程度高，但行进速度慢，通过设置与无人机相反的能力系数关系可增加距离对无人车产生的影响，使其倾向于优先探测近处的栅格。随着地图中min(P)不断增加，式（9）的第二项将逐渐趋近于0，将共同导引无人机与无人车对当前地图中探测程度较低的栅格进行探测，最终完成探测。充分发挥了无人机与无人车组成的异构协同在跨域协同探测中的优势。

（3）避障能力设计

无人平台行进过程中，为避免与障碍物及其他平台发生碰撞，设计当某一无人平台与障碍物或其他同空间域无人平台距离超过某一阈值时会受到二者产生的斥力，使得无人平台与障碍物及其他同域平台之间相互远离。

定义无人平台与障碍物之间斥力势场函数为

对式（10）求负梯度可得到障碍物与平台间斥力为

式中，η为斥力势场系数，d(q-qr)为平台与障碍物的距离，D为障碍物影响距离。

与上述过程类似，可定义无人平台之间的斥力势场与斥力。

最终使得无人车（无人机）行进过程中能避开周围障碍物及其他无人车（无人机），而无人机与无人车之间在相互靠近过程中不会产生斥力。

传统人工势场法由于单一且固定的目标点，引力方向始终指向该固定的目标点，可能会导致目标不可达等局部最优问题。本文所提方法中，由于地图探测程度不断改变，使得探测环境对某一无人平台的吸引力不仅大小在不断变化，吸引无人平台的目标栅格也在变化，从而避免了传统人工势场法的局部最优问题。

4 仿真结果及分析

为验证所提探测策略正确性及跨域协同探测的优势，搭建仿真环境进行验证。

4.1 未知探测区域环境搭建

设定未知区域环境大小为600 m×500 m；将未知区域划分为60×50 个栅格，则单个栅格大小为10 m×10 m。其中随机分布障碍物。

为方便直观展示协同探测效果，设计栅格颜色随探测程度的由低到高而逐渐变化，如图7（a）所示，其中0-1 表示地图探测程度，2 表征障碍物。

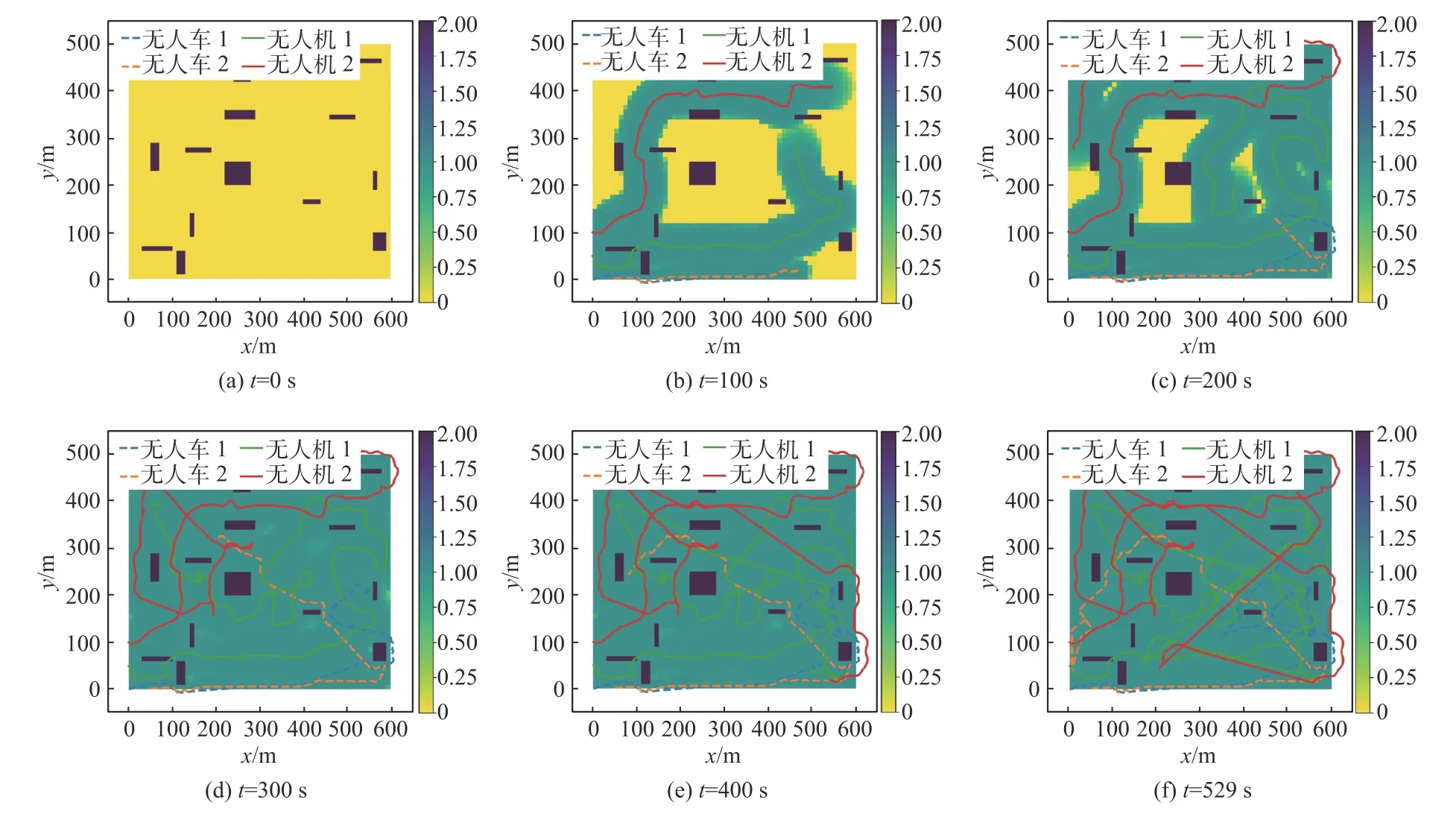
图7 2无人机与2无人车协同时不同时刻的探测结果Fig.7 The detection results of 2 UAVs and 2 UGVs at different times

4.2 协同探测策略合理性仿真验证

仿真验证过程中各参数取值如下：无人车速度v1=5 m/s，探测距离rdet=30 m，探测角度θdet=120°，探测能力k=0.8。无人机速度v2=10 m/s，探测距离r1=50 m，探测角度为360°，探测能力k=0.4。探测终止条件为环境栅格的最小探测程度Pmin＞0.9。

依据无人机与无人车优势特点与所设定的不同协同探测的策略，在势场导引函数即式（9）中为不同域的无人平台赋予不同的探测权重系数，分别为无人车k1=0.2，k2=0.8；无人机k1=0.8，k2=0.2。

仿真计算过程及结果如图7所示，图中实线为无人机探测轨迹，虚线为无人车探测轨迹。仿真结果表明：在探测初期阶段，无人机可充分发挥其飞行速度快、探测范围广的优势，在探测开始200 s 内其探测区域便覆盖了地图的大部分区域；无人车运行速度慢，虽然探测覆盖的面积与无人机相比较少，但探测程度高，其轨迹所覆盖的区域基本达到规定的探测程度。探测中期阶段，在探测开始200～400s 内，地图全部区域已完成探测覆盖，部分区域探测程度已达到所规定的标准。然而由于无人车探测视野受限，导致其在绕开障碍物继续向前探测后，探测视野盲区的探测程度较低；无人机探测程度较低，轨迹覆盖一次的探测程度不足。探测后期，无人机对障碍物周围无人车探测视野盲区开始快速补充探测，之后无人车配合无人机对地图中探测程度不足的区域进行共同探测。最终于探测开始529 s 后全部未知区域达到探测要求，探测完成。

由结果可知，无人机探测轨迹更远，探测范围更广，无人车探测程度更高，二者能充分发挥其优势特点，弥补探测过程中另一平台的不足，且不与周围障碍物发生碰撞，最终二者在较短时间内以规定的探测程度协同完成了未知区域的探测。可见本文提出的协同探测策略与仿真结果相符，一定程度上验证了本文所提出的协同搜索策略的合理性。

此外，通过仿真实验发现另一现象，即协同探测的无人平台规模不必无限增加，对此，本文给出了仿真计算结果如图8所示。

由图8可知，当分别固定无人机与无人车数量时，随着另一无人平台加入探测的数量不断增加，所需的探测时间不断减少，但改善程度不断降低。表明实际情况中，只需特定数量的无人平台便可高效地完成探测任务。

传统的区域覆盖探测往往采用覆盖路径规划算法。基于此，本文选取的对比算法为一种基于改进的A*算法的全覆盖路径规划算法［21］。改进的A*算法采用基于数量优化的24 邻域扩展，设置外层使用惩罚函数，内层设计变权重的启发函数。仿真条件设定与前文相同，设定无人车速度取v1=5 m/s，探测距离仍取rdet=30 m，探测角度θdet=120°，探测能力k=0.8；无人机速度取v2=10 m/s，探测距离取r1=50 m，探测角度为360°，探测能力k=0.4。仿真试验结果如图9 所示。在相同条件下与本文所提方法进行对比，本文所提方法完成探测时间为529 s，而基于改进的A*算法的传统全覆盖路径规划算法完成区域探测需要900 s。探究其原因，基于势场导引的协同探测方法摒弃了传统覆盖路径规划的规则行进路径，突破规则路径限制的无人平台能充分发挥其在探测过程中的优势，优先探测地图中探测程度较低的区域栅格，不规则的行进轨迹使得无人平台探测过程中的行进路径长度小于传统覆盖路径规划的路径长度，故探测时间能得以缩短。

图9 基于改进的A*算法的探测结果图Fig.9 The detection results based on the improved A * algorithm

5 结 论

本文针对未知区域的跨域协同探测问题，提出了一种通过势场为无人机与无人车提供导引的协同探测方法，能以较短的时间完成规定探测程度的协同探测任务。本文首先将未知区域栅格化处理，并通过颜色变化来表征栅格探索程度与障碍物，可方便计算与探测过程的直观展示。其次在协同探测过程中，通过分别为无人机与无人车设计不同的势函数来体现其在探测任务中的特点，使得无人机与无人车在探测过程中趋向于不同的探测方向，充分发挥其优势，实现了优势互补。最后搭建了仿真环境来验证提出的协同探测策略，结果表明：

（1）本文所提方法能充分发挥跨域异构无人系统的协同性，在较短时间内以规定的探测程度完成探测任务，且探测过程中不会和周围障碍物和其他无人平台发生碰撞。

（2）通过与某一具有一定代表性的传统覆盖路径规划算法进行对比，本文所提方法在相同探测条件下完成区域探测所需时间可减少约41%，在一定程度上验证了所提方法的优越性。

（3）当某一域平台数量固定时，随着另一种平台参与探测数量的逐渐增多，完成探测所需时间不断减少，但并非线性减少，而是缩减程度越来越低。表明实际情况中，需综合考虑无人机与无人车的各方面性能与成本等因素，只需特定数量的无人平台便可高效地完成探测任务。

在未来，可引入无人机与无人车之间的通信约束从而改善势场导引函数，使之更符合真实探测环境。