考虑工时不确定性的混流U 型装配线平衡的分布鲁棒优化方法

周剑扬， 张凌波

（华东理工大学信息科学与工程学院, 上海 200237）

多品种、小批量的产品需求模式使得混流U 型装配线为越来越多的制造型企业所采用。相较于直线单模装配线，混流U 型装配线具有可以同时生产多种类型的产品和工序分配更灵活等优点。因此，混流U 型装配线平衡问题（Mixed-Model U-Shaped Assembly Line Balancing Problem，MMUALBP）成为近几年的研究热点。目前已有许多研究人员针对理想情况下的MMUALBP 进行了研究[1-3]，但在真实的生产环境中，受工人熟练度等因素影响，装配时间并非固定值，为了抵消不确定工时带来的影响，提高装配线的鲁棒性就极其重要。

解决工时不确定装配线平衡问题的方法有随机优化（Stochastic Optimization，SO）、鲁棒优化（Robust Optimization，RO）和模糊规划等[4-10]。在工时的概率分布信息已知的基础上，SO 通过机会约束理论构建模型。文献[4]假设工时服从某个已知的正态分布，设定完工概率为α，建立了混合整数规划模型；文献[5]采用机会约束规划建立工时不确定情况下的Ⅱ类装配线平衡模型；唐秋华等[6]针对随机工时的装配线平衡问题，考虑物流运输约束条件，建立机会约束规划模型并转换为混合整数规划模型。RO 适用于工时部分已知的情况，通过集合的形式描述工时的不确定性。Hazir 等[7]针对时间的不确定性，建立基数不确定集合，构建了两种鲁棒优化模型，并提出一种基于分解的算法求解；Zhang 等[8]建立了时间不确定的Ⅱ类混流装配线平衡鲁棒优化模型，根据对偶原理将其转换为对等模型。模糊规划适用于存在模糊参数的最优化问题，其关键在于选择合适的隶属度函数。Mirzaei 等[9]采用梯形模糊数描述工时的不确定性，提出一种基于信念度的模糊模型；Babazadeh等[10]采用三角模糊数描述工时的不确定性并构建直型和U 型装配线模糊模型。

在上述文献中，SO 和RO 是两种常用的解决工时不确定条件下装配线平衡问题的方法，但却存在一定的不足。SO 需要知道完整的工时概率分布信息，在实际情况中很难实现；RO 不需要完整概率分布信息，在最坏情况下求解，结果通常较为保守。分布鲁棒优化[11-13]（Distributionally Robust Optimization，DRO）综合了SO 和RO 的优点，又在一定程度上解决了两者的不足，无需知道不确定参数确切的概率分布信息，同时又不忽略样本数据，通过构建不确定参数的模糊集，寻找极端概率分布下的最优决策。

本文考虑工时的不确定性，基于Wasserstein 距离[14-15]，建立工时不确定性模糊集，进一步建立MMUALBP DRO 模型，并根据对偶理论对原模型进行转化。针对提出的模型，设计了一种改进遗传算法（Improved Genetic Algorithm，IGA），提出一种基于区间数的解码方案，并引入自适应概率。最后通过数值仿真实验验证了所建立的DRO 模型可以更好地平衡效率和保守性，并进一步验证了IGA 在求解本文DRO 模型具有更好的精度。

1 基于Wasserstein 模糊集的分布鲁棒优化方法

1.1 分布鲁棒优化

DRO 最早由Scarf[16]在1958 年提出，其目标函数可以表示为：

1.2 基于Wasserstein 距离的模糊集

建尽可能小且包含真实分布的模糊集。本文采用Wasserstein 距离衡量经验分布和真实分布之间的差异，相较于其他度量，Wasserstein距离有着更好的性质[17]，定义如下：

1.3 数据驱动支撑集

2 工时不确定的混流U 型装配线平衡问题的分布鲁棒优化模型

2.1 问题描述

考虑工时不确定的第二类MMUALBP（MMUAL BP-Ⅱ）是在装配线工作站数量已知的情况下，最小化生产节拍。其每种产品每道工序的装配时间都是一个不确定的数值，工序时间的概率分布信息不可知，N个工序时间的历史样本数据已知。相较于普通的直线型单模装配线，混流U 型装配线的复杂性在于混流处理和工序分配。直型线的工序分配只能单向进行，而U 型线可以从前向后和从后向前双向进行。对于混流的处理，一般采取的方式是根据最小生产循环（Minimal Production Set，MPS）原理构建综合工序优先级图[21]，将“混流”问题转换为“单模”问题，如图1 所示，已知MPS 为1∶1∶1。

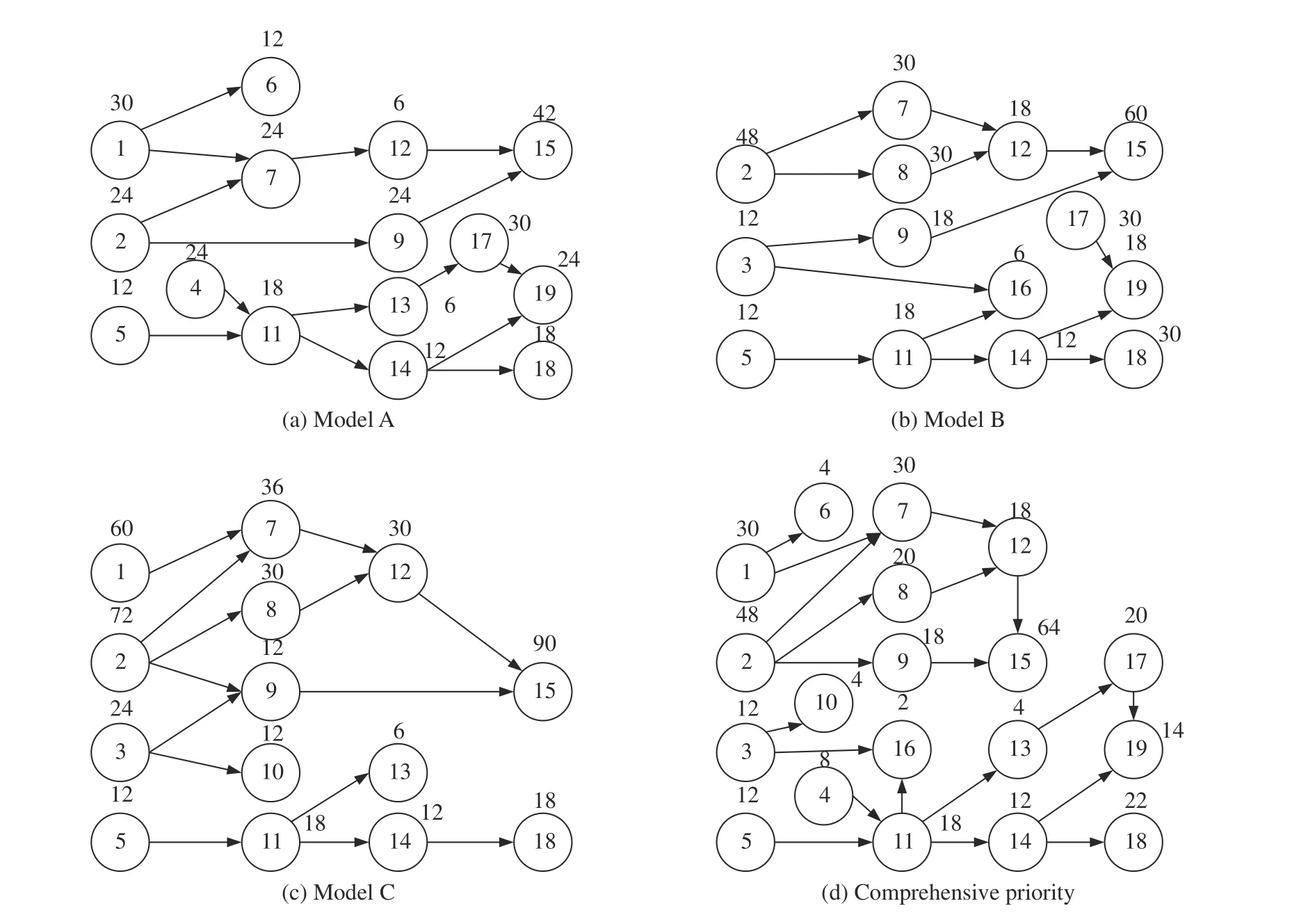
图1 综合优先级图Fig.1 Comprehensive priority chart

针对工时不确定的MMUALBP，提出几点假设：(1)工序的时间都是不确定的，但都服从轻尾分布；(2)所有模型的优先级图都可以构成综合优先级图；(3)不同的产品具有相似的工序，相同工序必须分配到同一个工作站；(4)所有模型相同工序的优先级关系相同。

2.2 混流U 型装配线平衡问题的分布鲁棒优化模型

针对工时不确定的MMUALBP-Ⅱ，优化目标定义为最小化生产节拍，DRO 模型可以表示为：

满足约束：

其中，E表示情景集，ztkCε为1 表示在情景ε中工作站k的总装配时间超过节拍时间tC，否则为0。参考上述方式，本文针对样本集提出一种鲁棒性指标RL：

3 改进的遗传算法

式(16)为产品的总需求；式(17)为综合优先级图中各工序根据MPS 计算得出的加权时间；式(18)表示每道工序都被分配至一个工作站；式(19)表示工作站的总时间不得超过节拍时间；式(20)和式(21)分别表示向前和向后的工序分配需要满足优先级约束。其中：M为模型数量，m=1.2,···,M；dm为MPS 中模型m的需求；D为所有模型需求总量；K为工作站数量，k=1,2,···K；J为工序数量，j=1,2,···J；t˜jm为模型m的工序j装配时间；T˜j为工序j的加权时间；tC为节拍时间；当分配顺序从前向后、工序j分配给工作站k时，xjk为1，反之为0；当分配顺序从后向前，工序j分配给工作站k时，yjk为 1，反之为 0；Pr为工序优先级矩阵。

2.3 分布鲁棒模型的对偶转化

根据强对偶原理，将DRO 模型中求极端分布期望问题转化为易于计算的形式：

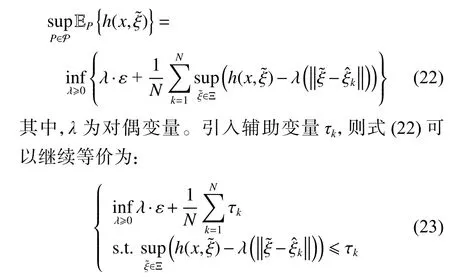
2.4 鲁棒性指标

鲁棒性指标用于衡量分配方案的鲁棒性，一般通过工作站的过载情况衡量方案的鲁棒性[22-24]。文献[24]中通过方案正常运行的比例作为衡量鲁棒性的指标Rrob，并将其作为模型约束，具体可以表示为：

装配线平衡问题是典型的非确定性多项式难问题（NP 问题），当问题规模较小时，可以采用精确算法快速求解，当问题规模较大时，精确算法的求解效果较差，甚至无法求解，因此，越来越多的研究人员采用智能优化算法进行求解。遗传算法[25](Genetic algorithm，GA) 是基于达尔文进化论的智能优化算法，因为其简单、求解速率快等优点被广泛应用于各领域问题的求解。本文提出一种用于求解上述模型的IGA。

3.1 编码和解码

针对MMUALBP-Ⅱ，IGA 采用优先级权重的编码方式，初始对每道工序赋予[0,1]之间的随机数，作为该工序的权重系数，以Jackson 问题为例，其优先级权重编码如图2 所示。

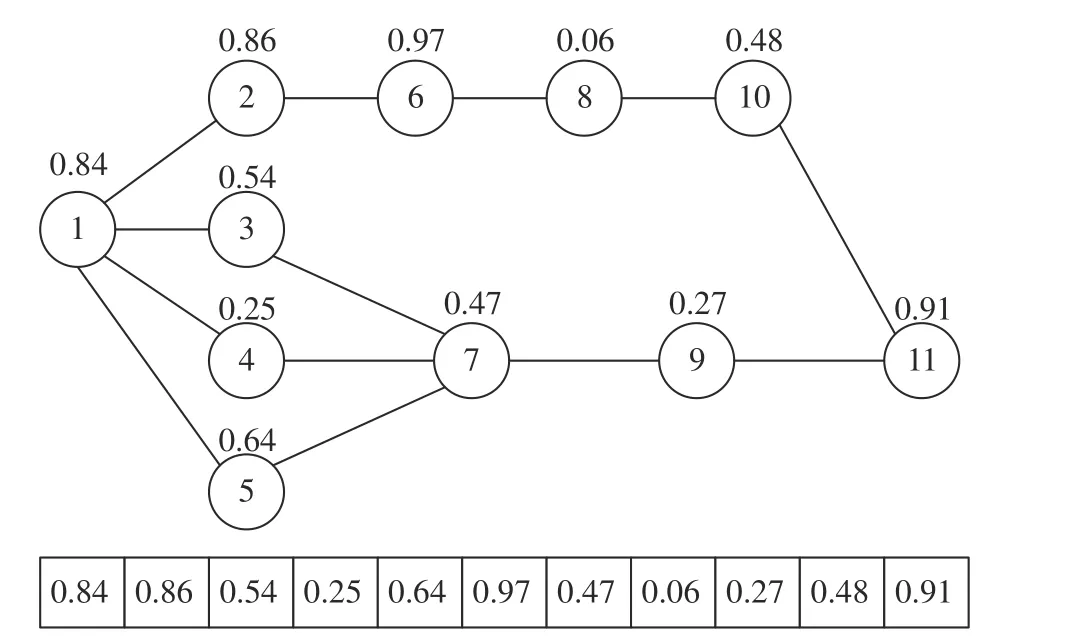
图2 Jackson 优先级权重编码Fig.2 Jackson priority weight coding

根据URBAN[26]提出的影子约束关系（图3），同时从前后两个方向进行工序分配，具体步骤如下：

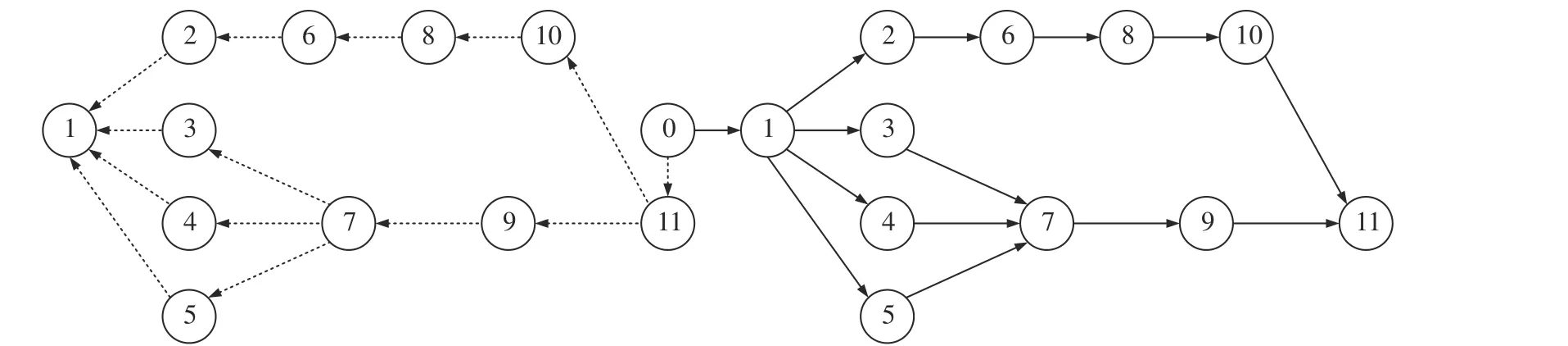
图3 影子约束关系图Fig.3 Shadow constraint diagram

步骤6：如果k=K-1，将剩余工序分配至工作站K，输出分配结果，否则k=k+1，转至步骤2。

3.2 适应度函数

适应度代表个体在种群中生存的优劣程度，IGA 的适应度函数可以表示为：

3.3 选择操作

IGA 采用轮盘赌选择法进行个体选择，其思想是个体被选择的概率与适应度大小成正比，可以描述为：

其中，P(xi)为个体xi被选中的概率。

3.4 交叉操作

IGA 采用实数编码，因此交叉操作采用模拟二进制交叉。首先需要生成[0,1] 内的均匀分布随机数u，然后根据u计算传播因子βa：

其中：p1和p2均为亲代个体，c1和c2均为交叉后产生的子代个体。

3.5 变异操作

变异操作中随机选择染色体中某个基因，用[0,1]区间中的随机数替换，过程如图4 所示。

图4 变异过程Fig.4 Variation process

3.6 自适应交叉和变异概率

为改善GA 易于陷入局部最优的问题，IGA 引入了自适应交叉概率Rc和变异概率Rm，根据种群的权重编码排序结果调整变异和交叉的概率，使得种群在聚集程度高的时候提高变异概率，降低交叉概率，而在聚集程度低的时候提高交叉概率，降低变异概率。

其中，Diff_Num 表示权重大小排序后不相同的个体数，Size 表示种群总数。

4 标准算例测试与分析

4.1 实验设计和环境参数

为了验证所提模型和算法的性能，采用https://assembly-line-balancing.de/中的混流数据集作为标准数据，如表1 所示。与确定性优化（Deterministic optimization，DO）、SO 和RO 方法比较，SO 模型参考文献[4]，置信水平取95%，RO 模型参考文献[8]，区间扰动系数ψ取0.1，DRO 中置信水平β和η均取95%。实验中假定所有工序的装配时间tjm不固定，且满足轻尾分布的假设。为了模拟真实环境，以标准时间为期望，以0.1 倍的期望作为方差，生成200个样本数据。模型的求解采用IGA 和GA，种群大小设置为30，精英保留数为2，迭代次数为500，IGA 初始的变异和交叉因子分别设置为0.2 和0.5，GA 恒定为0.1 和0.8，测试指标为节拍时间，为避免随机性，对每个算例独立运行10 次。测试软件为Matlab2021b，测试环境为11th Gen Intel(R) Core(TM) i7-11800H @2.30 GHz，16 GB RAM。

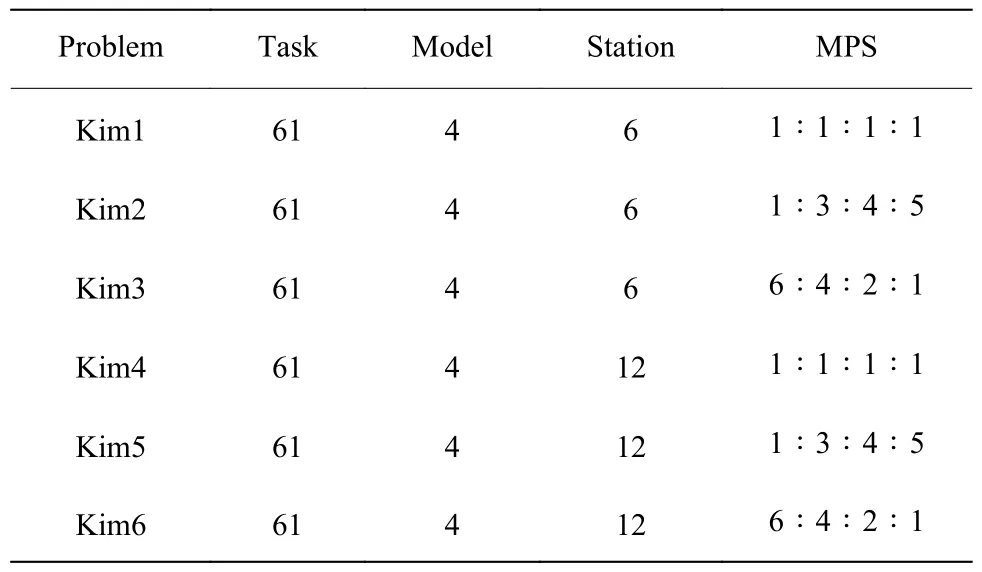
表1 测试算例Table 1 Test examples

4.2 测试结果与分析

表2 给出了问题Kim1～6 的测试结果，从最优生产节拍指标最优值（Best）看，SO 所求得的节拍时间最小，DRO 次之，RO 最大。对于上述结果，因SO 已知工时的概率分布信息，可以求得最小的节拍时间，而RO 考虑最坏情况最差值（Worst），故所得的节拍时间最大，DRO 则是利用了历史数据信息，通过求取极端分布的情况下期望上界，因此所获得的节拍时间介于SO 和RO 两者之间。根据不同样本个数对比结果可以看出（表3），随着样本数量的增加，DRO得到的节拍时间会减少。这是因为随着样本数量N的增加，Wasserstein 球的半径会逐渐降低，使得模型的保守程度降低。从表2中DRO+IGA 和DRO+GA的对比结果来看，IGA 相较于GA，在Kim1～6 问题的求解上都得到了更小的生产节拍，均值（Mean）和标准差（Std）的值也表明IGA 的稳定性更好，仅在Kim4 中IGA 的Std 值差于GA，这说明在求解本文模型上，IGA 的性能要优于GA。

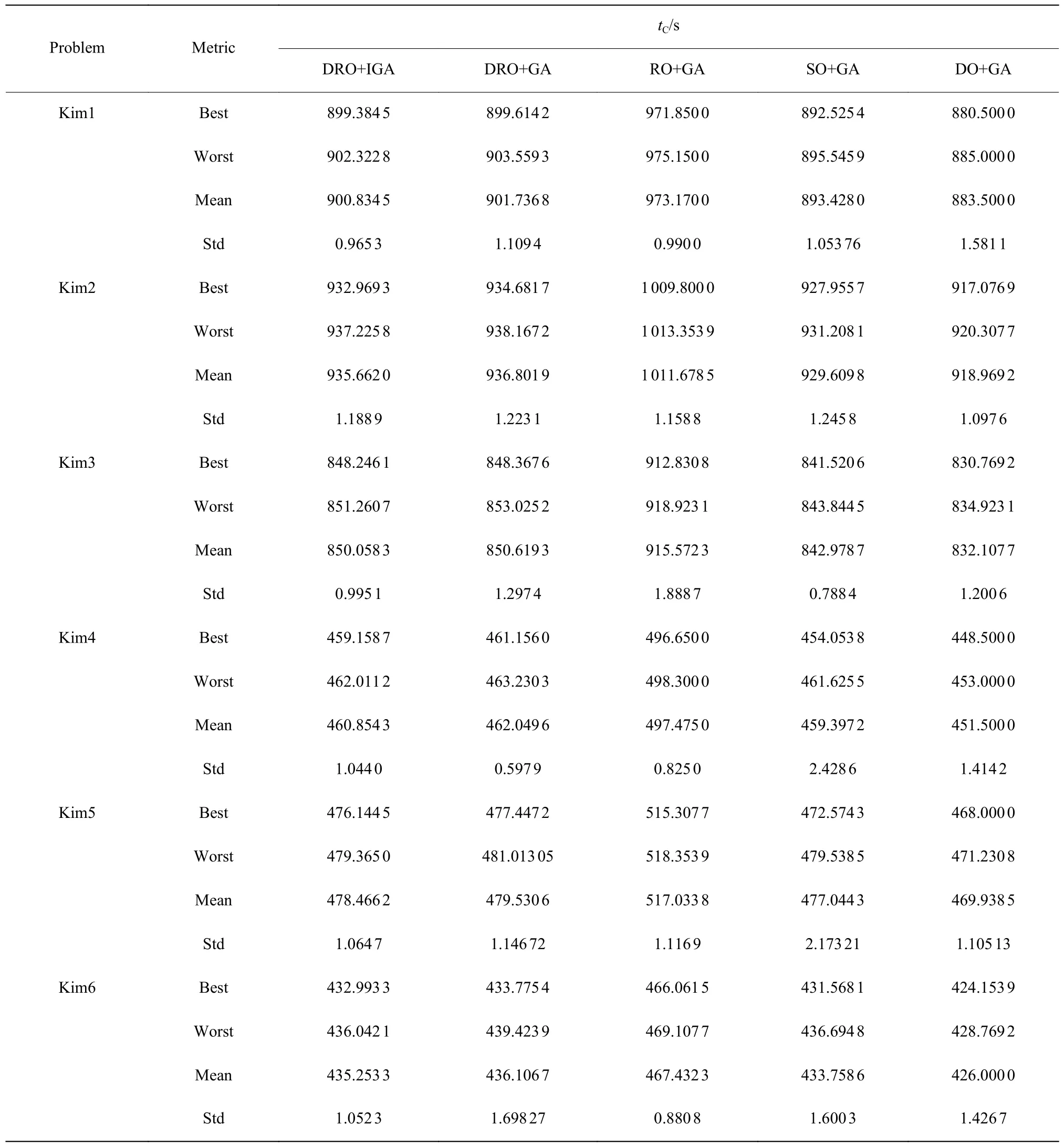
表2 对比测试结果Table 2 Results of comparison test

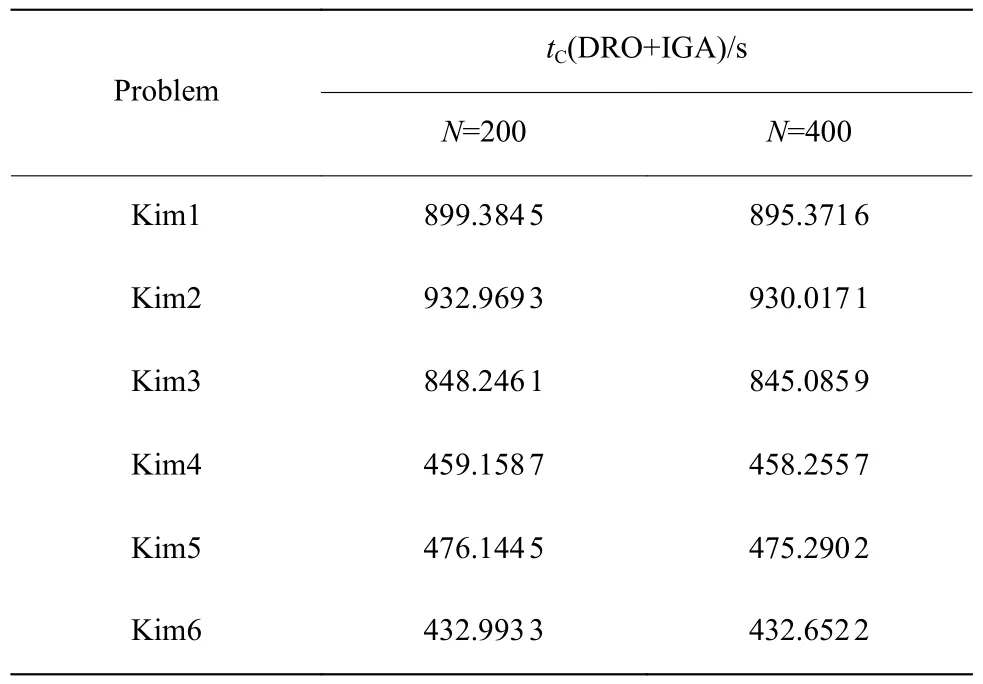
表3 不同样本个数对比结果Table 3 Comparison results of different sample numbers

为进一步验证模型解的鲁棒性，采用相同的方式生成10 000 条样本数据，分别计算三种模型解的鲁棒性指标值，结果如表4 所示。SO 模型虽然已知装配时间的概率分布信息，但在生产环境中可能和实际运行中的数据存在偏差，不能应对所有可能的场景，因此所得解的鲁棒性较低；RO 模型因为考虑最坏情况，因此能完全应对时间不确定性所带来的扰动，所得解的鲁棒性最高，其RL值均达到1；DRO模型因为考虑样本数据和极端分布的情况，所得解的鲁棒性介于SO 和RO 之间，但RL值基本接近1 的程度，说明DRO 模型具有较好的鲁棒性。图5 给出了更加直观的结果，其中f代表频率。

表5 给出了SO、RO 和DRO 3 种模型的鲁棒代价（POR）。参考文献[27]，鲁棒代价可以通过下式计算：

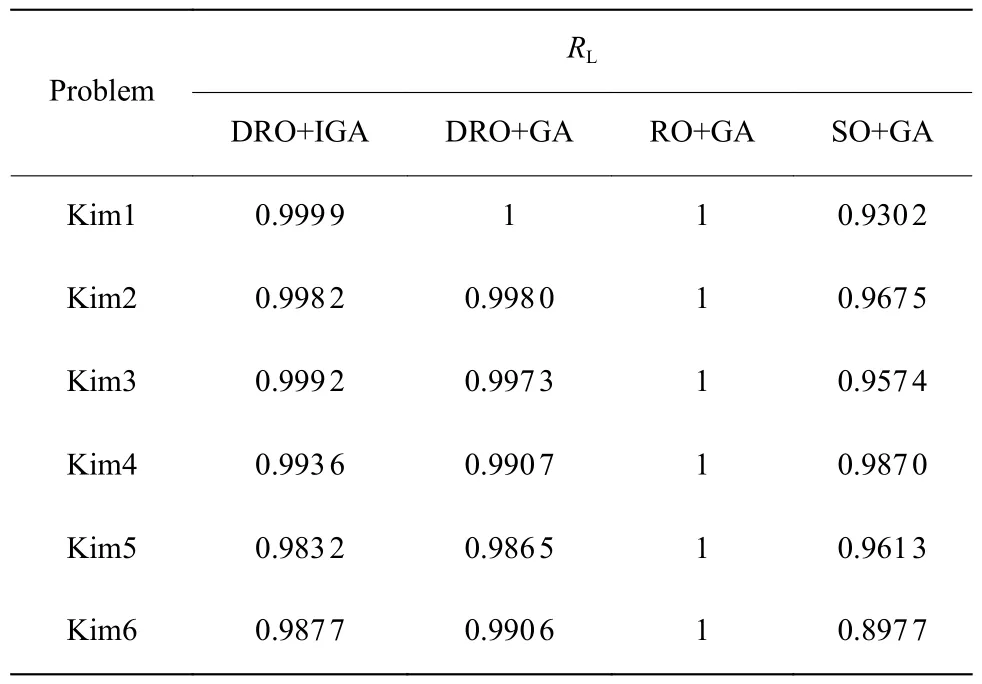
表4 鲁棒性指标对比结果Table 4 Comparison results of robustness metric

表5 3 种模型的鲁棒代价Table 5 Price of robustness for three models

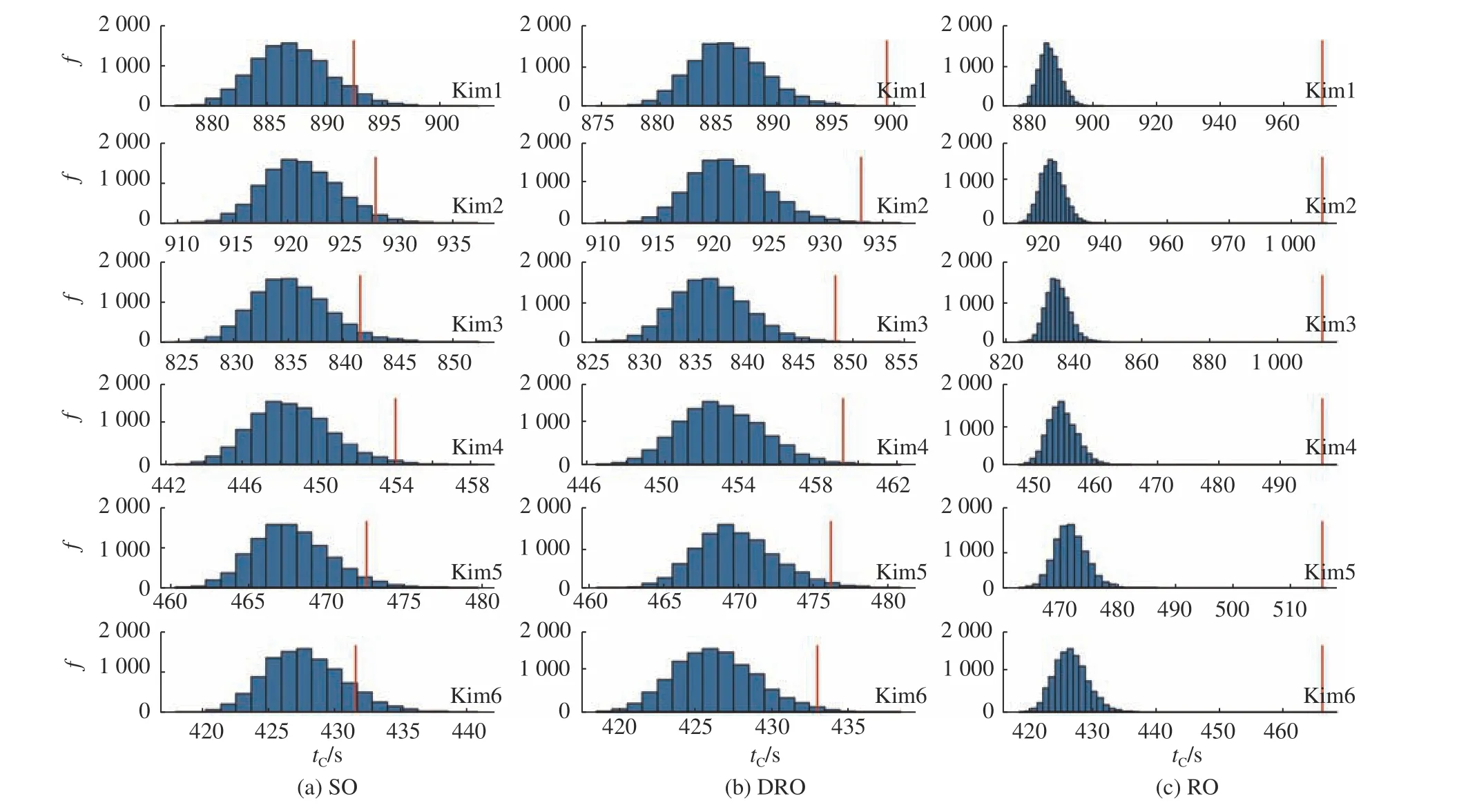
图5 不同模型目标值和实际生产节拍对比Fig.5 Comparison of object value and actual cycle time of different models

其中，xDO表示确定性优化的最优决策，xmodel表示工时不确定条件下模型做出的最优决策，f(·)表示决策所对应的节拍时间。如表5 所示，在Kim1～6 中表现出的鲁棒性代价关系为SO 最小，RO 最大，DRO 介于SO 和RO 两者之间，说明为了应对工时的不确定性，SO 模型所做出的决策付出的代价最小，RO 付出的代价最大，而DRO 介于SO 和RO 之间。结果表明，SO 的 保 守 性 最 低，RO 最 高，DRO 介 于SO 和RO 之间。

5 断路器生产实例分析

某公司断路器抽架装配线为包含14 个工作站的混流U 型装配线，可以生产A、B、C、D 四种型号的产品。抽架装配过程包含机构装配等56 道工序，具体的工序时间和工序优先级关系如表6 和图6 所示。表6 中所示的装配时间（t）为测得的标准时间，由于装配时间受到工人熟练度、环境等影响存在波动，在进行装配线平衡时需要考虑这种不确定性。

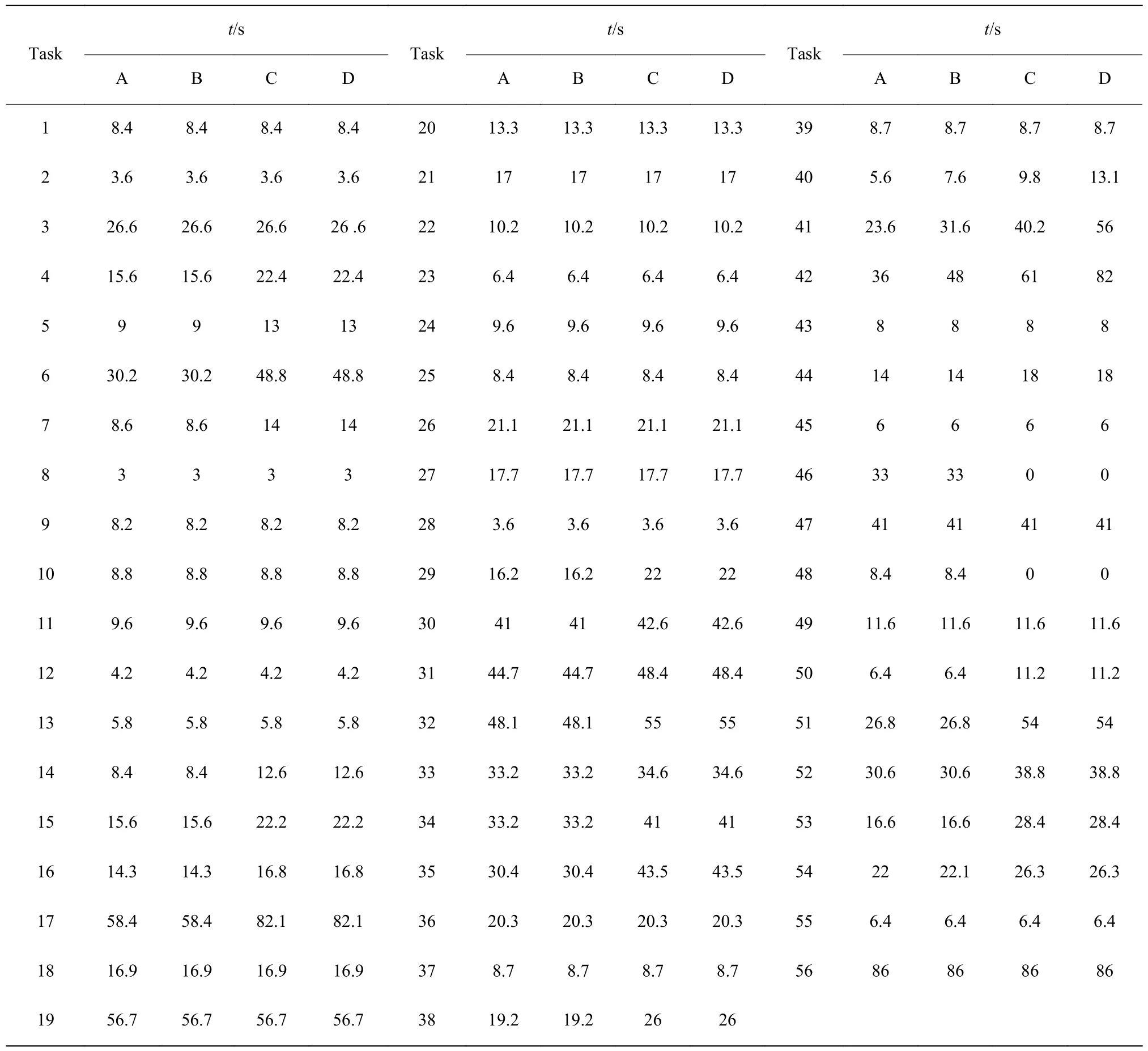
表6 断路器抽架工序信息Table 6 Chassis process information of circult breaker

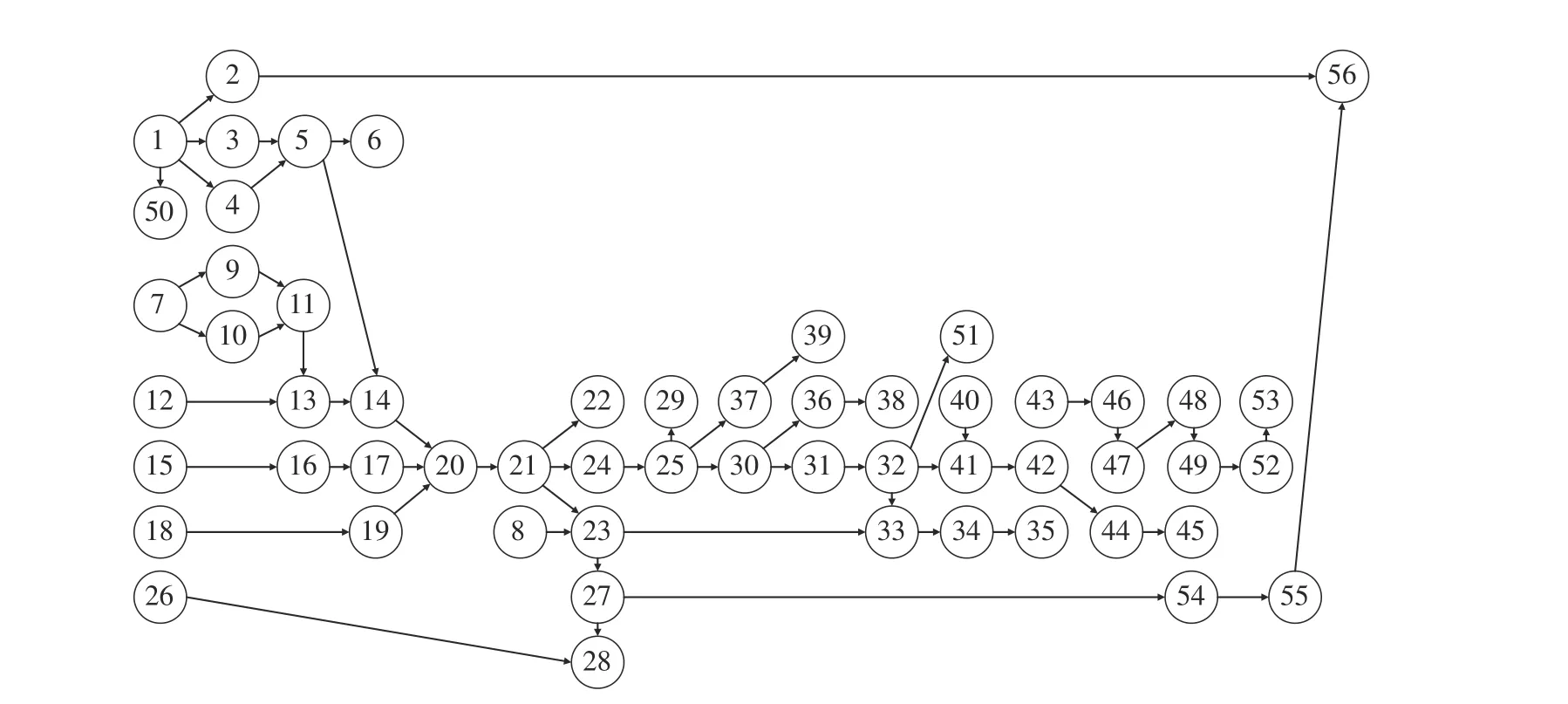
图6 断路器抽架工序优先级关系图Fig.6 Circuit breaker chassis process priority diagram

真实的生产环境中各工序的装配时间通常围绕标准时间上下随机波动，因此可以采用高斯分布生成数据模拟真实数据，具体的生成方式和相关参数设置与本文第4 节相同。当MPS 为1∶1∶1∶1 时，测试指标为最优生产节拍，采用IGA+DRO 的方式，优化前节拍时间为149 s，优化后为92.7 s，随机样本测试的鲁棒性指标值为0.960 7，优化前后的工序分配见表7。相较于原方案，在工时不确定的情况下，采用DRO+IGA 优化后的装配线具有更小的节拍时间，说明该装配线得到了很好的优化，各工作站的负载更为均衡，同时所设定的节拍时间和工序分配方案可以很好地抵抗工时不确定性带来的扰动，使得装配线具备较好的鲁棒性。

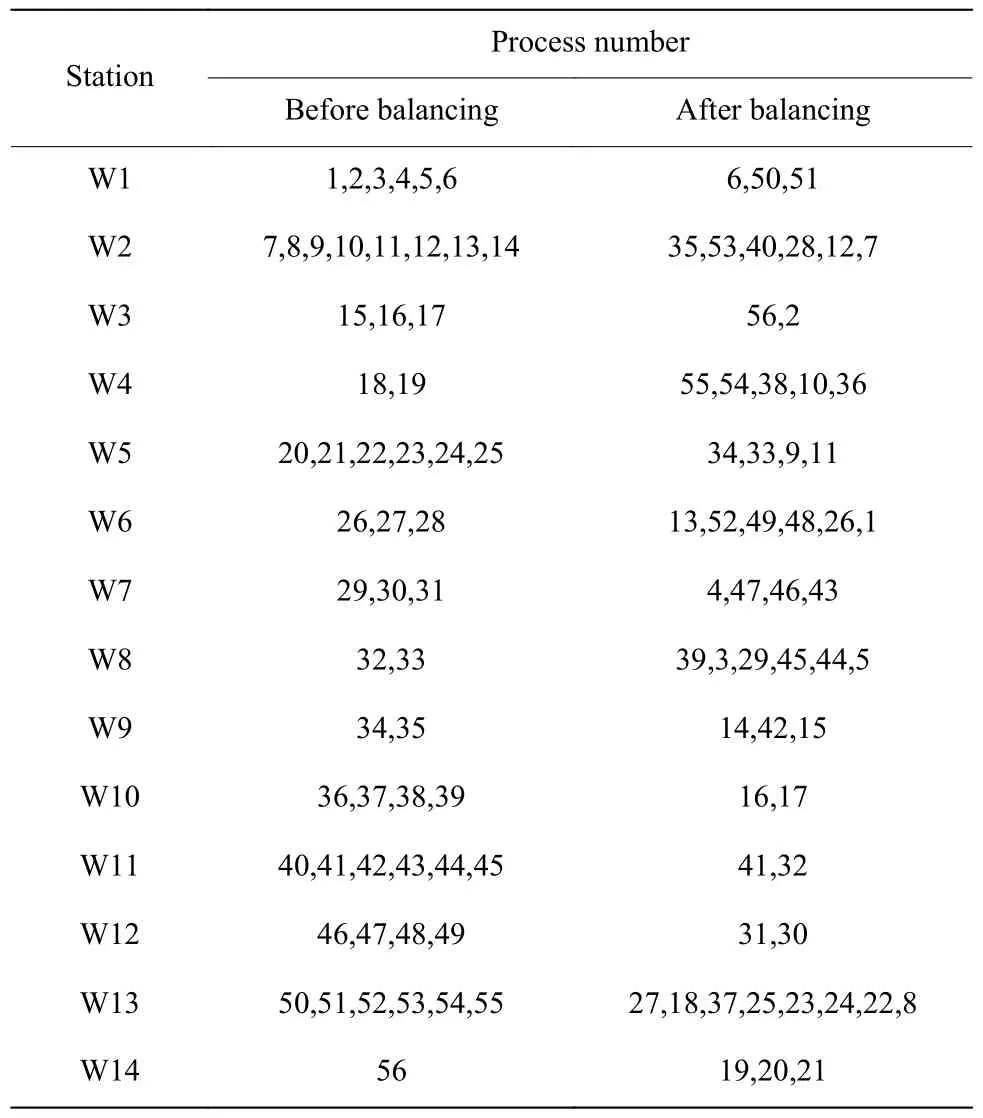
表7 工序分配Table 7 Distributing of process

6 结 论

本文采用一种基于Wasserstein 距离的分布鲁棒优化框架对工时不确定的MMUALBP-Ⅱ进行建模；以样本推导的经验分布为中心，以Wasserstein 距离为度量，构建模糊集并建立了DRO 模型，通过对偶转换，将原模型转化为易于求解的形式；设计了一种基于工作站过载情况的鲁棒性指标，并将其作为模型约束，增强解的鲁棒性；同时提出一种改进的遗传算法用于上述模型的求解，采用自适应交叉和变异因子，并设计了一种基于区间数的解码方案；通过标准的测试用例，验证了IGA 相较于GA，在求解上述模型上的性能更好，同时验证了所建立的DRO 模型相较于一般的SO 和RO 模型，在保证解具有较高鲁棒性的同时，节拍时间有所降低，并且随着样本数量的增加，节拍时间还会进一步降低；最后通过断路器抽架案例，进一步验证了所提模型的有效性，为解决该类工程问题提供了参考方案。