地下预制管廊纵断面抗震设计的反应位移法

梁建文,官其铝,李东桥,赵 华

(1. 天津大学 建筑工程学院,天津 300350; 2. 天津市建筑设计院,天津 300074)

0 引言

地下结构的常用抗震分析方法有自由场变形法、土-结构相互作用系数法、反应位移法、反应加速度法和时程分析法等多类方法,其中反应位移法由于具有物理概念明确、计算步骤简单等优点在我国多部规范[1-2]中被采用,主要用于地下结构横断面和纵向抗震设计。

目前,已有不少学者开展了地下结构反应位移法的研究。刘晶波等[3]采用土-结构动力相互作用法对反应位移法进行理论推导,结果表明反应位移法理论基础较为严密。王国波等[4]研究了反应位移法中常用的简化和假设对结构地震响应的影响。景立平等[5]在现有静力有限元法的基础上,设计了6种求解反应位移法中地基弹簧系数的静力有限元方法。杜修力等[6]基于反应位移法的基本原理,提出了一种适用于复杂断面地下结构抗震分析的方法。一些学者还将反应位移法应用到地下综合管廊的抗震分析问题中。施有志等[7]探讨了反应位移法在地下综合管廊抗震分析中的适用性,研究表明在地下管廊的初步抗震计算中可优先选用反应位移法。梁建文等[8-9]采用反应位移法和壳-弹簧模型计算了预制地下管廊的纵向地震响应和横断面地震响应,研究了地下管廊的抗震性能。

以上研究讨论了反应位移法及其在地下综合管廊抗震分析中的适用性,然而,值得指出的是,目前反应位移法仅适用于地下管廊横断面和纵向抗震分析,尚未有用于纵断面抗震分析相关的研究。随着地下综合管廊的发展,管廊横断面尺寸越来越大,目前已出现双层甚至多层的管廊,在地震作用下,管廊结构将在纵断面内承受更大的地层变形;同时,对于预制管廊,由于预制接头弱化了结构的整体刚度,管廊结构纵断面内的转动和层间变形将更为显著,可能导致管廊结构出现损伤。然而,目前针对地下管廊的抗震分析仍多为横断面地震响应或纵向地震响应分析[10-13],尚未有学者讨论地下管廊的纵断面地震响应。

鉴于此,本文在传统横断面反应位移法的基础上进行拓展,讨论了地下结构纵断面抗震分析的等效地震荷载构成,提出一种分析地下预制管廊纵断面地震响应的反应位移法(简称纵断面反应位移法),并验证了方法的可靠性。以某拟建的地下预制单层管廊和双层管廊为例,研究了地震作用下,管廊的纵断面层间变形行为以及薄弱部位。相关方法可为地下预制管廊的纵断面抗震设计提供参考。

1 纵断面抗震设计的反应位移法

1.1 传统的横断面反应位移法

对于匀质或层状半空间内的地下结构,考虑地震波垂直入射情况,其系统的运动方程可由式(1)所示:

(1)

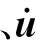
图1 传统横断面反应位移法计算模型Fig. 1 Traditional cross-section response deformation method model

对于传统横断面反应位移法,为保证地下结构边界位置的应力条件和位移条件与原自由场一致,施加在结构边界处的地震作用如式(2)所示:

(2)

由于拟静力分析忽略阻尼力的影响,则结构系统的平衡方程可由式(3)所示:

(3)

可以看到,传统横断面反应位移法中,作用于地下结构的等效地震荷载由三部分组成,即结构与土交界面上的剪应力、相对位移和结构自身的惯性力。

1.2 纵断面反应位移法

对于纵断面反应位移法,同样将地下结构对应土体的变形、剪应力与结构自身的惯性力施加于结构以完成等效地震荷载的输入,但纵断面反应位移法输入的等效地震荷载构成与传统横断面反应位移法存在差异。根据一维土层地震反应规律,同一深度土层变形保持一致,水平面内无剪切变形和剪应力作用,为保证计算模型边界与原自由场地截断处的应力条件一致,结构侧墙将无土体的剪应力作用,施加于结构顶底板的等效地震荷载包括土体相对位移、土体剪应力和结构自身的惯性力。本文纵断面反应位移法计算模型的等效地震荷载如图2所示。

注:kn和kt分别为地下结构上的法向地基弹簧刚度和切向地基弹簧刚度; (zU)和(zB)分别为结构顶板和底板处单位面积上作用的剪应力; Δu(z)为深度z处土体相对位移; f(z)为结构自身在深度z处的惯性力。图2 纵断面反应位移法计算模型Fig. 2 Model of longitudinal-section response deformation method

由图2可知,对于纵断面反应位移法计算模型,模型前后侧墙上并无土体剪应力作用,仅需考虑原自由场的位移条件,由式(2)可得前后侧墙处的荷载形式为:

Fn(z)=0

(4)

Ft(z)=kt·Δu(z)

(5)

对于顶底板,需同时考虑原自由场的位移和应力条件,其荷载形式为:

Fn(z)=0

(6)

(7)

基于传统横断面反应位移法思想,本文纵断面反应位移法也将地下结构对应土体发生最大相对位移时刻(最不利时刻)地震荷载施加在结构上。

综上,对于本文纵断面反应位移法,施加于管廊结构的等效地震荷载如表1所示,其中,相对位移施加在地基弹簧远端。

表1 等效地震荷载Table 1 Equivalent seismic load

2 算例与分析

2.1 计算模型参数

某拟建的地下预制单层管廊和双层管廊,单层管廊横断面总宽度为11000mm,其中大舱宽度6100mm,小舱宽度4900mm,高度为5750mm,顶板和侧墙厚度为550mm,底板厚度为600mm,中隔板厚度为300mm,横断面尺寸如图3所示。双层管廊横断面总宽为9500mm,左边舱室宽度为6350mm,右边舱室宽度为3150mm,总高度为7300mm,层高均为3650mm,顶板和底板厚度为600mm,侧墙厚度为550mm,中隔板厚度为300mm,横断面尺寸示意图如图4所示。

图3 单层管廊横断面尺寸Fig. 3 Cross-section dimension of single-layer utility tunnel 图4 双层管廊横断面尺寸Fig. 4 Cross-section dimension of double-layer utility tunnel

单层管廊和双层管廊预制标准节段的长度为1500mm,混凝土强度等级为C60,其在弹塑性状态下应力和损伤因子与非弹性应变的关系由文献[14-15]确定,钢筋强度等级为HRB400,具体配筋见文献[8]。预制装配式管廊预制标准节段间通过企口接头连接,标准节段间的相互作用宏观上表现为接头处的止水橡胶和混凝土的协同受压和受剪作用,在有限元软件中采用非线性弹簧模拟预制标准节段间的企口接头,接头弹簧刚度根据止水橡胶及混凝土的力学性能确定[14-16],具体布设方案见文献[8]。

地下预制管廊处于水平成层场地中,场地总厚度为80m,埋深为3m。场地共有8个土层,各土层力学参数如表2所示,土体动剪切模量和阻尼比与剪应变之间的关系如表3所示。

表2 土层参数Table 2 Soil layer parameters

表3 土体动剪切模量和阻尼比与剪应变之间的关系Table 3 Relationship between soil dynamic shear modulus and damping ratio and shear strain

入射地震波选为E2(中震)及E3(大震)安评波,峰值加速度分别为0.2g和0.38g,如图5所示。

图5 安评波时程Fig. 5 Time history of seismic evaluation waves

利用ABAQUS有限元软件,建立地下预制管廊壳-弹簧模型[8]。采用S4壳单元模拟管廊结构,网格尺寸为0.75 m×1 m。采用地基弹簧来模拟土体与结构的相互作用,在法向上,土体对地下预制管廊不存在拉力,故法向地基弹簧只有压缩刚度;在切向上,土体与地下预制管廊可能会发生相对滑移,因此地基弹簧需要设置屈服位移,由地下预制管廊所在土层的属性确定屈服位移值为0.01 m[17]。采用GB 50909—2014《城市轨道交通结构抗震设计规范》[1]中的推荐公式计算地基弹簧刚度,地基土的基床系数由GB 50267—2019《核电厂抗震设计规范》[18]确定。单层管廊和双层管廊有限元模型如图6和图7所示。

图6 单层管廊有限元模型Fig. 6 Finite element model of single-layer utility tunnel

图7 双层管廊有限元模型Fig. 7 Finite element model of double-layer utility tunnel

2.2 管廊计算长度的确定

首先需要确定模型计算长度,以避免模型边界效应对计算结果的影响。本文以管环标准段的纵断面层间变形为参考指标[19],采用纵断面反应位移法计算模型长度分别为100a(150 m)、64a(96 m)、48a(72 m)和32a(48 m)等4个工况下单层管廊的纵断面地震响应,中震作用下,其结果如图8所示,其中,a为预制标准节段长度。

图8 层间变形分布图Fig. 8 Distribution diagram of deformation between layers

由图8可知,不同计算长度下,计算模型的纵断面层间变形沿管廊纵向均呈现稳定的一致分布规律,由于结构在模型端部的约束弱于中部,因此层间变形在模型端部出现突变。本文将层间变形超过单层管廊中点处数值5%的区域定义为边界影响区域,不同计算长度下,单层管廊计算模型的边界影响区域范围约为6a(9 m),为避免边界条件对计算结果的影响,将计算模型长度取为48a(72 m)。

2.3 模型验证

本文借鉴隧道结构抗震分析的广义反应位移法思想[20],将一维地震反应得到的土体变形、应力及结构惯性力时程作为等效时程荷载施加于计算模型,计算地下管廊结构的纵断面动力响应,将该方法称之为时程分析法。

采用纵断面反应位移法和时程分析法计算了单层管廊和双层管廊等2种管廊结构的纵断面地震响应,中震作用下,本文2种方法的计算结果如图9和图10所示。其中时程分析法计算结果提取时刻为7.84 s。

由图9和图10可知,2种方法的截面内力在无边界影响范围内沿管廊纵向呈现稳定的一致分布,总体趋势保持一致,其中,截面剪力沿管廊纵向方向近似正对称的分布形式,截面弯矩近似反对称的分布形式。对应于管廊中点的截面内力和层间位移角如表4所示。

图9 单层管廊截面内力对比图Fig. 9 Comparison of the internal force of the single-layer utility tunnel

图10 双层管廊截面内力对比图Fig. 10 Comparison of the internal force of the double-layer utility tunnel

表4 截面内力和层间位移角数值对比Table 4 Comparison of the internal force and interlayer displacement angle value

当地下预制管廊在纵断面内产生层间变形时,结构将在纵断面内产生转动,此时结构将产生截面剪力和截面弯矩。可以看到,单层管廊和双层管廊纵断面反应位移法模型与时程分析法模型的截面剪力、截面弯矩和层间位移角数值较为接近,最大相对误差分别为1.2%、6.4%和2.0%。由于管廊在纵断面内产生层间变形,并未发生整体纵向拉压变形,因此截面轴力数值通常比较小,工程意义不大,与一般地下结构纵向抗震分析中因纵向拉压变形导致的截面轴力存在本质差别。

综上,可以看出,本文纵断面反应位移法计算结果较为准确,可用于分析地下预制管廊的纵断面地震响应。

2.4 管廊损伤分析

为分析地下预制管廊沿纵断面发生层间变形时结构的损伤情况,使用本文纵断面反应位移法计算了中震和大震等2种工况下管廊的响应,单层管廊中间预制标准节段的受拉损伤如图11所示。

图11 单层管廊受拉损伤Fig. 11 Pull damage of single-layer utility tunnel

文献[21]指出当混凝土的抗拉强度下降至峰值的一半时发生破坏,对应的损伤因子达到限值,本文中混凝土的受拉损伤限值为0.153。由图11可知,在中震作用下,单层管廊受拉损伤首先出现于中隔板下缘,大震作用下,受拉损伤扩展至结构侧墙,模型最大受拉损伤达到0.98,已严重超出限值,因此,进行地下预制管廊的纵断面抗震设计是十分必要的。

双层管廊中间预制标准节段的受拉损伤云图如图12所示。由图可知,在中震和大震作用下,双层管廊均出现受拉损伤超限的情况,且损伤峰值大于单层管廊。尤其是在大震作用下,不仅双层管廊侧墙出现损伤超限的情况,结构的顶板和底板位置也发生严重的损伤超限。

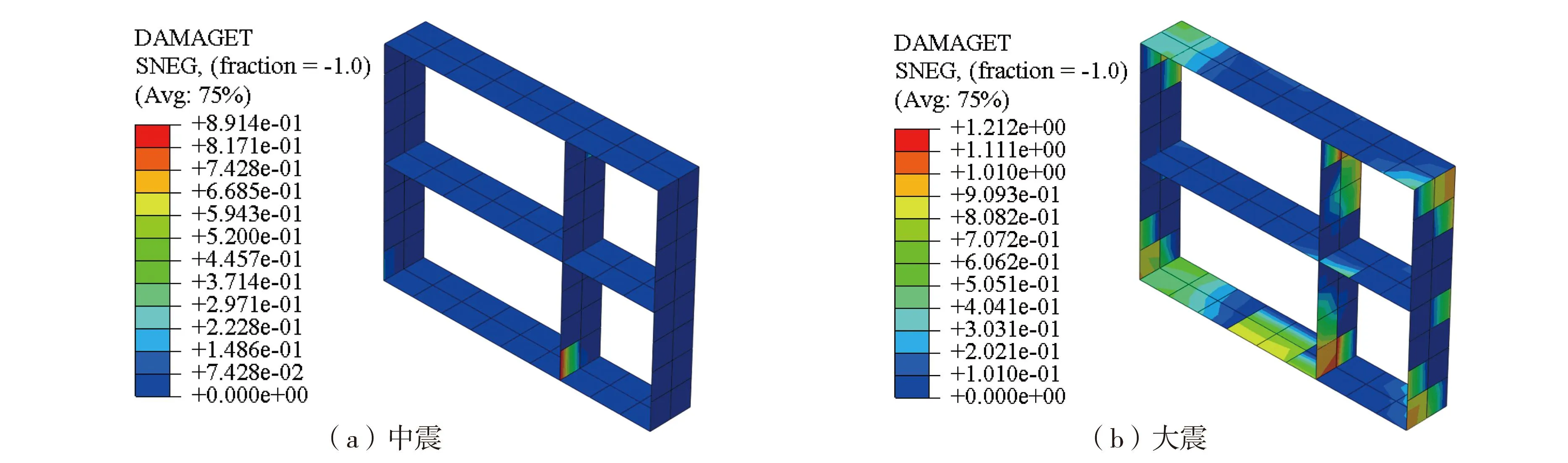
图12 双层管廊受拉损伤Fig. 12 Pull damage of double-layer utility tunnel

由图11、图12可知,双层管廊纵断面地震响应大于单层管廊,管廊结构高度越大对结构抗震越不利。另外,值得注意的是,受拉损伤严重的区域出现在结构中隔板端部和侧墙位置,因此应该考虑加强该区域的构造配筋。

3 结论

基于传统横断面反应位移法的基本原理,本文提出地下结构纵断面抗震设计的反应位移法,以某拟建的地下预制管廊为例进行纵断面抗震设计,对结构的内力、变形和损伤展开讨论,得到如下结论:

1)本文所提地下预制管廊纵断面抗震设计的反应位移法,考虑了地下结构在地震作用下沿纵断面发生层间变形时的等效地震荷载,适用于均匀场地或水平成层场地中规则断面的地下管廊的抗震设计,可为地下预制管廊等地下结构的纵断面抗震设计提供参考。

2)本文算例中的单层管廊和双层管廊在中震作用下均出现受拉损伤超限,混凝土发生受拉破坏,且双层管廊内力、变形和受拉损伤均大于单层管廊,表明结构高度越大对其纵断面抗震性能越不利。因此对地下预制管廊,尤其是高度较大的地下预制管廊进行纵断面抗震设计十分必要。损伤超限大多发生在结构侧墙以及中隔板端部,在工程设计时应加强这些位置的抗震设防,可增强结构侧墙以及中隔板的配筋。