淤砂层对重力坝地震响应的影响分析
2024-01-05刘田田陈少林张艳红
刘田田,陈少林,张 娇,张艳红
(1. 南京航空航天大学 民航学院,江苏 南京 210016; 2. 南京航空航天大学 航空学院,江苏 南京 210016;3. 中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100048)
0 引言
为了充分开发利用水能能源,满足不断增长的能源需求和改善能源结构,我国已建和正在新建的水利水电高坝枢纽工程,其规模和数量在世界上都是史无前例的。然而,我国位于世界上2个最活跃的环太平洋地震带和欧亚地震带交汇部位,是全球遭受地震灾害最为严重的国家之一,并且我国水能资源的70%~80%集中在构造运动强烈、地质环境不稳定、地震活动显著的西部地区,这对高坝的抗震设计与安全性评价提出了严峻挑战[1]。
国内外学者对重力坝的地震响应及破坏做了很多研究[2-5],但传统重力坝抗震设计中,使用有限元模拟大坝结构地震响应时,库水可压缩性对坝体地震响应的影响尚不明确。WESTERGAARD[6]最开始研究库水对坝体-坝基体系相互作用的影响,假设了水体不可压缩和库底不吸收边界,这种假设不能考虑库水可压缩性及库底沉积层与坝体及地基之间的相互作用,难以真实地反映出库水及沉积层对多耦合体系的影响。王进廷[7]的研究结果表明,在垂直地震动作用时,库水自振频率对作用于坝体的动水反应影响显著,因此不可忽略库水可压缩性。CHOPRA[8]的研究表明,库水可压缩性在某些情况下可以削弱坝体地震响应,而某些情况下又可以放大坝体地震响应。因此,库水可压缩性对坝体的影响尚需进一步研究。
为了研究库底淤砂层对水坝地震响应的影响,杜修力等[9]将淤砂模拟为固液两相多孔介质,揭示了淤砂层不仅有吸收库水地震反应能量的作用,而且存在惯性放大效应,且随淤砂层厚度而变化;王进廷等[10]将淤砂层分别模拟为线弹性固体、黏弹性固体、理想流体和黏性流体等不同介质,并与将淤砂层模拟为两相多孔介质的结果进行比较,建议在高坝-库水-淤砂层-地基系统地震反应分析时,根据淤砂层的渗透系数与饱和度,选择两相多孔介质或简化的黏弹性固体介质模型;YAN等[11]将淤砂层考虑为两相多孔弹塑性介质,认为淤砂层降低了地震加速度响应和动水压力,有利于坝体安全;王怀亮[12]将坝体视为弹塑性材料,发现淤砂层的存在降低了坝面最大位移和最小位移峰值,且随淤砂层厚度增加,影响逐渐加大。
为考虑库水可压缩性和淤砂层的影响,以及库水、淤砂层、坝体和坝基之间的耦合,国内外学者进行了很多研究。L∅KKE等[13]、CHOPRA[14]考虑流体和固体的耦合,将淤砂层的影响近似用一个反射系数表示;王进廷等[15]、赵成刚等[16]、杜修力等[17]将淤砂模拟为流体饱和多孔介质,利用流体饱和多孔介质、弹性固体介质、理想流体介质的动力反应分析方程以及3种介质的界面耦合条件,建立了坝-库水-淤砂-基岩系统的动力响应分析模型,但此方法需要对3种介质微分方程进行离散,并在界面处根据不同的连续条件进行两两耦合,比较复杂。为解决上述问题,分析库底沉积淤砂的影响,本文考虑库水可压缩性,将淤砂层视为饱和多孔介质,在广义饱和多孔介质统一计算框架中考虑库水(流体)、坝体、坝基(固体)、淤砂层(饱和多孔介质)间的耦合,建立库水-淤砂-坝体-坝基体系的地震反应分析模型,将地震作用下库水-淤砂-坝体-坝基体系的响应问题当作半无限域中的波动散射问题,发展相应的求解方法。
1 基本理论
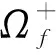

图1 库水-淤砂层-坝体-坝基体系模型Fig. 1 Reservoir water-sediment-dam-dam foundation system model
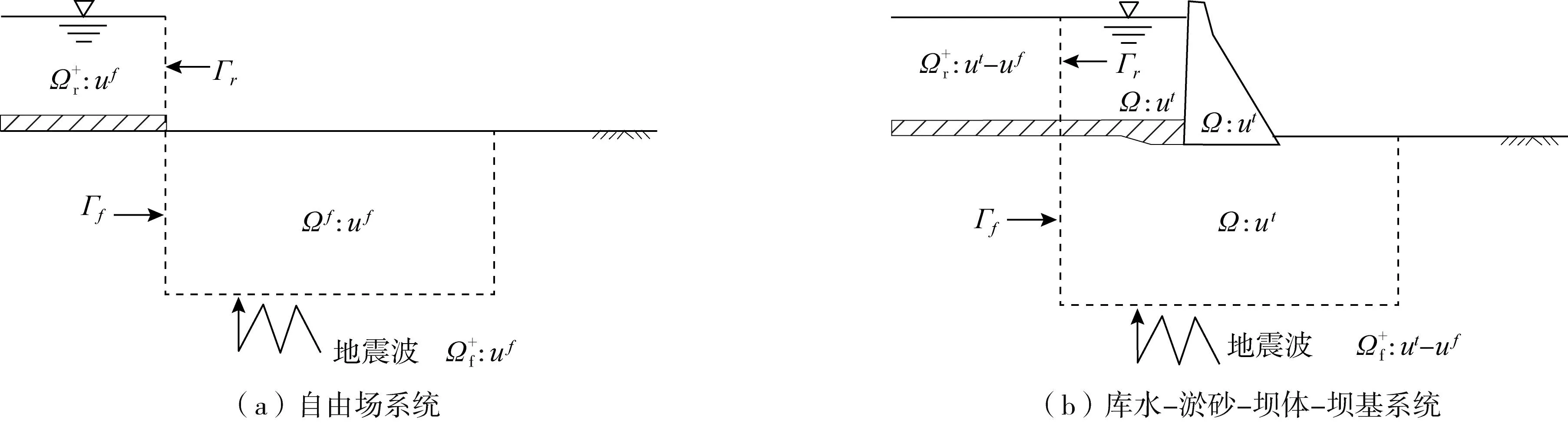
图2 库水-淤砂层-坝体-坝基体系组成Fig. 2 Composition of reservoir water-sediment-dam-dam foundation system
1.1 自由场分析
自由场分析可为波动散射问题提供输入,假定平面波入射,其分析模型如图2(a)所示。考虑坝体上、下游模型不同,自由场计算分为2个模型,一个是下游的基岩自由场模型,一个是上游的库水-淤砂层-基岩自由场模型。
1)基岩自由场
按照弹性成层半空间的理论,采用传递矩阵方法,可得到基岩侧的自由场响应uf[20-21]。基岩半空间的入射波可按传递矩阵方法由控制点地震动反演得到;若为均质半空间,垂直入射时,则将控制点地震动折减一半作为由基岩半空间输入的入射波时程。
2)库水-淤砂层-基岩自由场
根据水的声波方程、BIOT[22-23]饱和多孔介质运动方程、弹性介质的波动方程,以及各界面边界条件,采用传递矩阵方法,可得到水平成层的库水-淤砂层-坝基体系响应uf和Uf,输入波由式(1)中的方法确定。
1.2 库水-淤砂层-坝体-坝基系统分析
内部计算区域采用有限元离散如图2(b)所示,计算区域的有限元节点可分为内部节点和人工边界节点,内部节点又分为一般内部节点(包括自由表面节点)与不同介质交界面上的界面节点。
1.2.1 内部节点
根据文献[24]可知任一节点i的运动平衡方程为:
(1)
(2)
式中:Msi、Mwi分别为集中在节点i上的固、液相质量;Fsi、Fwi分别为集中在节点i上的固、液相本构力;Tsi、Twi分别为集中在节点i上的固、液相黏性阻力;Ssi、Swi分别为作用在节点i上的固、液相界面力。
对式 (1)、式(2) 进行时步积分, 可得到内部节点i的固、液相位移递推公式:
(3)
(4)
节点i为一般内部节点时,界面力Ssi、Swi为零。节点i为界面节点时,采用隔离体概念,将界面节点分离成第一种介质中的节点i和第二种介质中的节点k组成的节点对。推导[20-21]可得固、液相法相界面力如下:
(5)
(6)
式中:
A11=(Δt)2β(msi+msk)
(7)
(8)
(9)
(10)
(11)
(12)
其中:
(13)
(14)
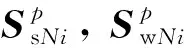
(15)
1.2.2 人工边界节点
由于透射边界不依赖于具体的波动方程,具有普适性和简便性的特点,本文人工边界条件采用多次透射公式(multi-transmitting formula,MTF)[25]:
(16)
其中:
(17)

2 算例分析
2.1 模型及材料参数
选取Koyna重力坝的一个挡水坝段进行分析。Koyna坝的几何尺寸参考文献[14],最大坝高103m,坝顶宽14.8m,坝底宽70.2m。库水深为92m,模型地基范围上、下游、深度方向各取2倍、2倍和1.5倍坝高,建立库水-坝体-坝基体系耦合模型,采用四边形单元对模型进行离散,如图3所示,本算例中取淤砂层厚度h=0。模型各材料参数参考文献[14],如表1所示。

图3 有限元模型Fig. 3 Finite element model

表1 模型材料参数Table 1 Material parameters of the model
2.2 脉冲波输入
输入如图4所示的脉冲波,脉冲宽度为0.1s,持续时间为12.0s(图4(a)只给出了0.6s),时间步距Δt=2.0×10-4s。分别考虑P波和SV波于坝基底部垂直入射。

图4 脉冲波输入Fig. 4 Pulse wave input
根据坝体受力特性选取上游坝踵、坝顶、下游折坡处、坝趾4个监测点(A-D),以及库水表面监测点E,如图3所示。P波入射时,位移时程如图5所示,波场快照如图6所示,只给出了反应较大的主方向。由于波在自由面的放大效应,坝顶和折坡处位移响应较大,约为坝踵和坝趾的2倍;库水表面点位移也较大,且由于在坝基和自由面间来回反射,持时相对于坝体点较长。

图5 P波垂直入射A~E点Z方向位移响应Fig. 5 Displacement response of P wave perpendicular incidence at point A~E in Z direction

图6 P波垂直入射波场图Fig. 6 Wave field snapshots of P wave perpendicular incidence
由图6所示的波场快照可以看出,入射波由底部入射,0.05s时,底部位移达到脉冲的最大值。0.07s左右,脉冲峰值到达基岩表面,放大2倍,达到最大值;由于坝体波速大于淤砂和库水,同一高度处,坝体先于库水有反应(如0.1s时坝顶达到峰值后,0.13s库水表面才达到峰值)。0.17s左右,坝顶反射波到达坝底后再反射,反射系数小于零,坝体位移为负,此时库水中位移波峰值经表面反射后还未抵达基岩面。0.23 s左右,库水位移波峰值已抵达基岩面并反射,库水位移为负,0.1~0.23s,可明显看出经坝体散射的散射波场。1s后,坝体和基岩反应很小,库水中的波在基岩面和自由表面之间来回反射,消散较慢。
SV波垂直入射时的位移响应和波场图如图7和图8所示。由图7可知,由于放大效应,在坝顶的位移较大,折坡处初始阶段的2个峰值分别为入射波和经坝顶的反射波,坝体后期进入明显的自由振动阶段,其衰减是材料阻尼和辐射阻尼引起的。受坝体运动的激发,临近坝体的库水位移时程(E点)与坝体B点类似。由图8的波场图可知,SV波由底部向上传播,到达库水与基岩界面处,由于库水不能受剪,波不能由基岩传入库水。坝体开始有反应后,坝体的激励引起库水的反应。坝体内的波在坝顶和坝基处来回反射形成驻波,按一阶模态振动,并由于阻尼作用反应慢慢消散。

图7 SV波垂直入射A~E点X方向位移响应Fig. 7 Displacement response of SV wave perpendicular incidence at point A~E in X direction
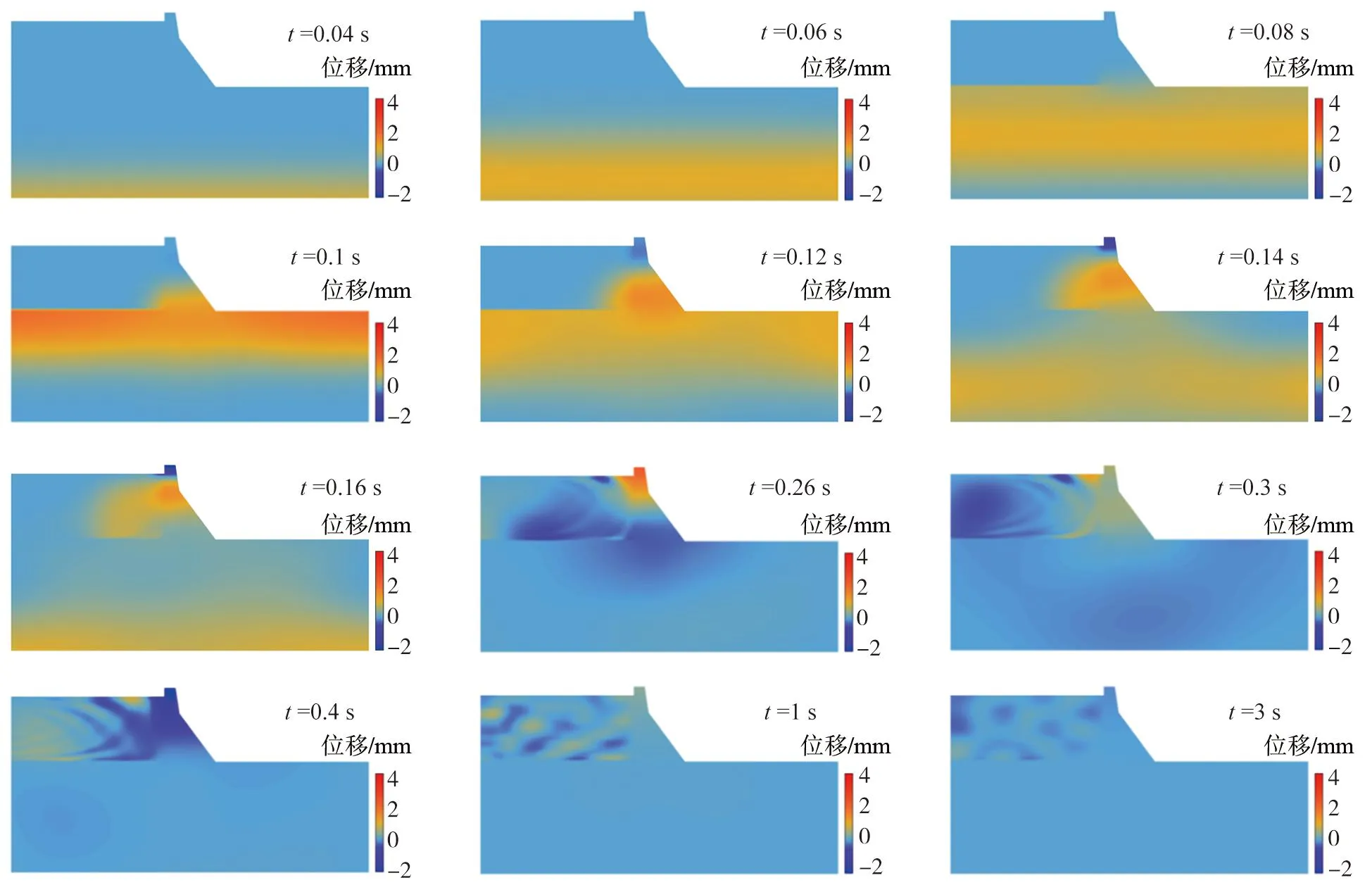
图8 SV波垂直入射波场图Fig. 8 Wave field snapshots of SV wave perpendicular incidence
2.3 地震波输入
1967年Koyna地震,在Koyna坝的一个坝段上记录到图9所示的水平和竖向地震加速度时程,由于离基岩面较近,将其近似为露头基岩面处的地震动,分别按SV波和P波垂直入射,反演得到坝基计算面处的入射波,进行双向地震动输入时的反应分析。

图9 输入地震波Fig. 9 Seismic wave input
坝体各监控点的位移、速度、加速度时程分别如图10~图12所示。由图可知,相对速度和加速度而言,各监控点的位移相差不大,主要是由于位移由低频控制,波长相对于坝体尺寸较大,坝体对低频波的散射作用很小。速度和加速度中、高频成分丰富,受坝体散射作用明显,各监控点的速度和加速度相差较大,坝踵(A点)和坝趾(D点)加速度峰值接近,坝顶(B点)的水平向加速度峰值约为坝踵(A点)的5倍,竖向加速度峰值接近4倍;折坡处(C点)的水平向加速度峰值和竖向加速度峰值分别约为坝踵(A点)的2倍。
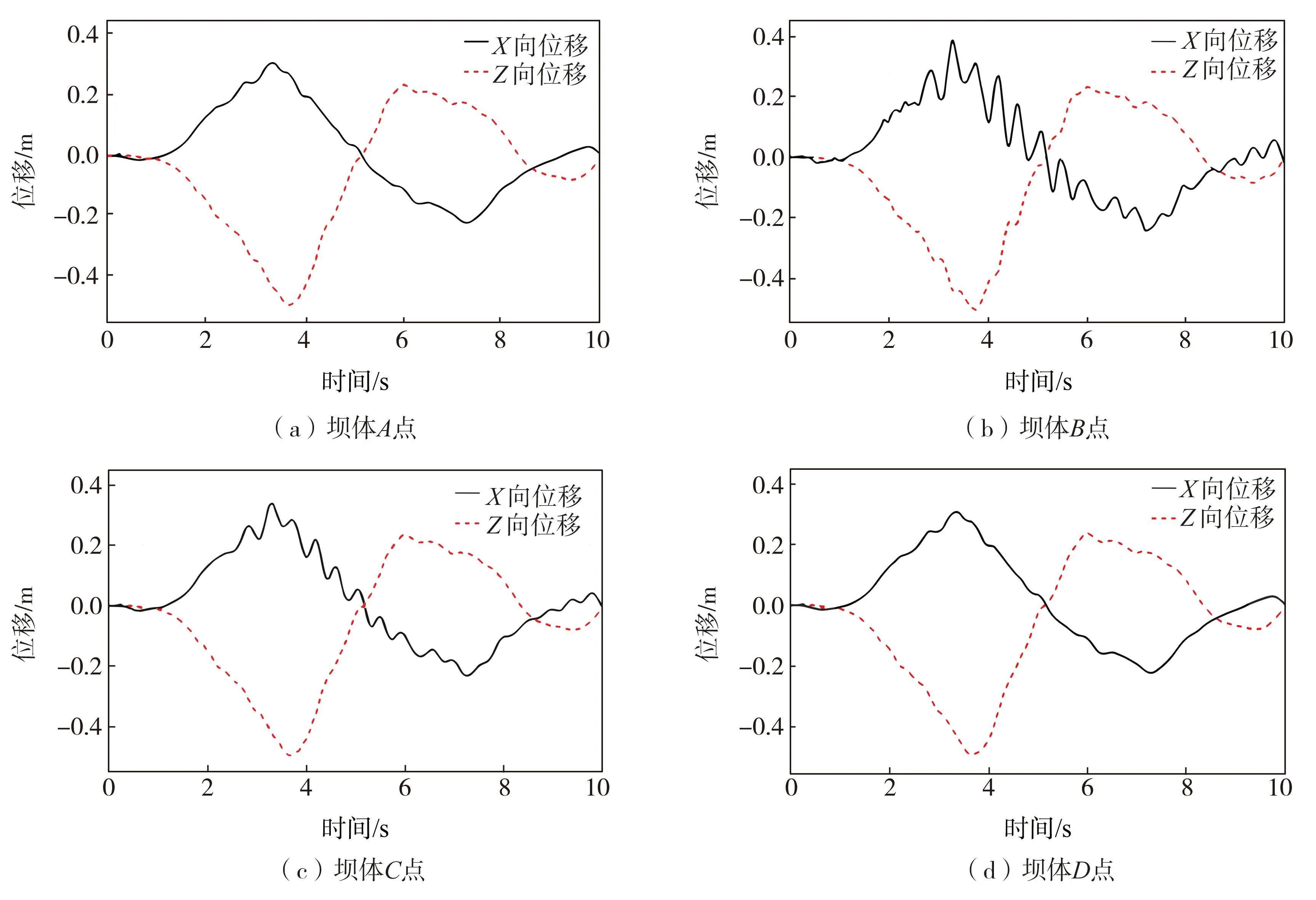
图10 坝体A~D点位移时程图Fig. 10 Displacements at point A~D of dam
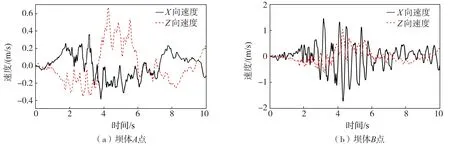

图11 坝体A~D点速度时程图Fig. 11 Velocity time history diagram at point A~D of dam
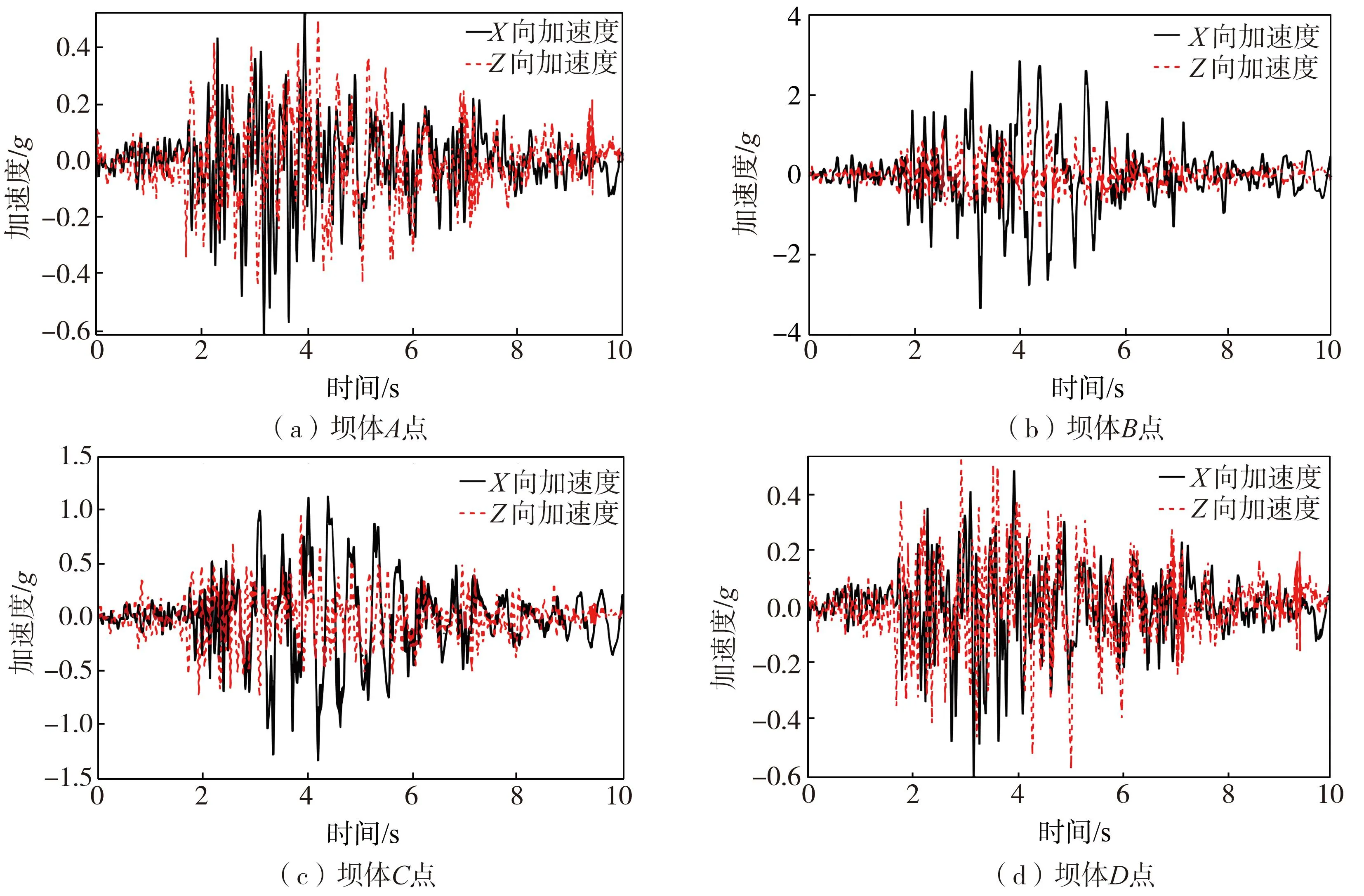
图12 坝体A~D点加速度时程图Fig. 12 Acceleration time history diagram at point A~D of dam
2.4 淤砂层厚度对坝体地震响应的影响
为了分析不透水基岩层上淤砂层对坝体的影响,设计了如下4个工况模型:
工况1:不考虑库底淤砂层的影响,认为库底没有淤砂层,库水直接与不透水基岩接触;
工况2:考虑库水下均匀分布着淤砂层,淤砂层厚度为8m,保持水库水位与工况1相同;
工况3:将工况2的淤砂层厚度改为16m,保证水库水位和其他条件不变;
工况4:将工况2的淤砂层厚度改为24m,保证水库水位和其他条件不变。
4种工况全部使用表1的材料参数,同样在基岩底部垂直输入图9所示地震波。
图13~图15为坝体监测点的位移和加速度时程,由图可知,库底淤砂层对坝体位移的影响不大,对加速度有影响,降低了坝体加速度峰值。

图13 坝踵(A点)X、Z向位移Fig. 13 Displacement of dam heel in X and Z directions
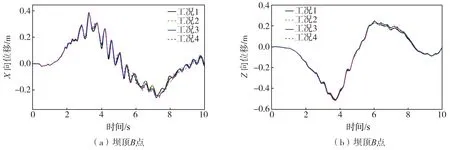
图14 坝顶(B点)X、Z向位移Fig. 14 Displacement of dam crest in X and Z directions
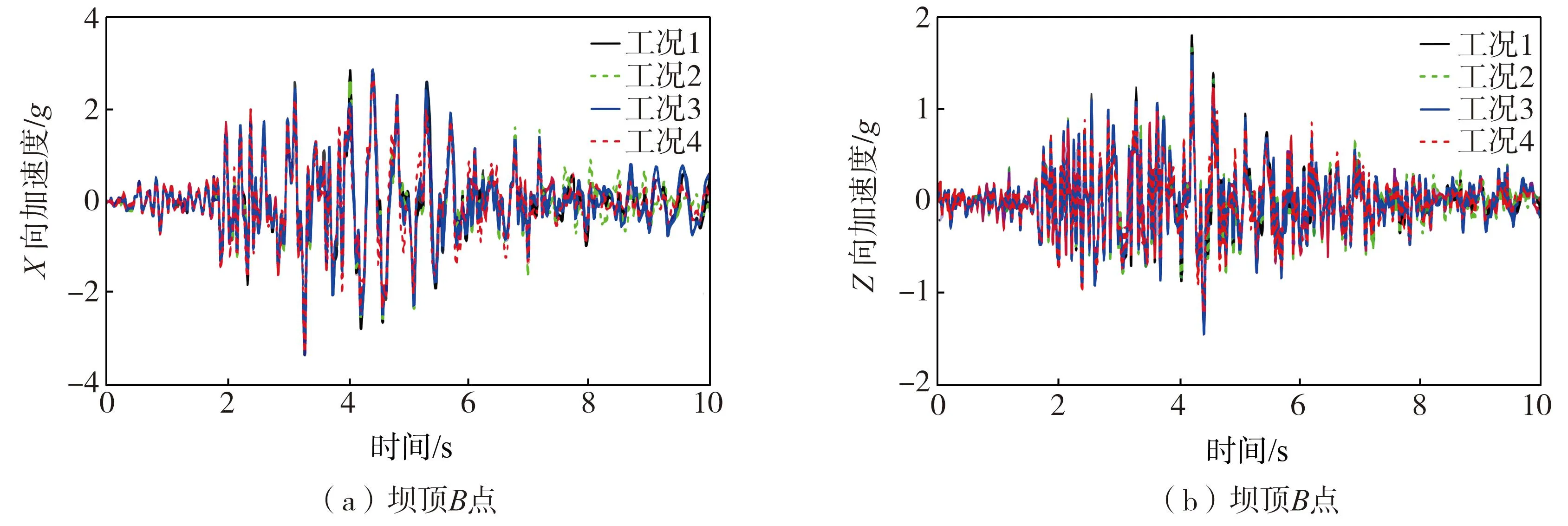
图15 坝顶(B点)X、Z向加速度Fig. 15 Acceleration of dam crest in X and Z directions
输出坝体各点的最大拉、压应力(以拉为正,压为负),由图16、图17以及表2所示,可以看出上游坝面、坝踵区域,折坡处及下沿区域的最大拉应力和压应力相比坝体其他节点较大,最大拉、压应力均出现在折坡处。淤砂层对坝体应力分布有一定的影响,随着淤砂层厚度的增加,上游坝面尤其是坝踵区域的最大拉、压应力明显逐渐减小;折坡处及下沿区域最大拉应力和最大压应力逐渐减小,但变化不明显;坝趾区域最大拉应力和最大压应力均减小。
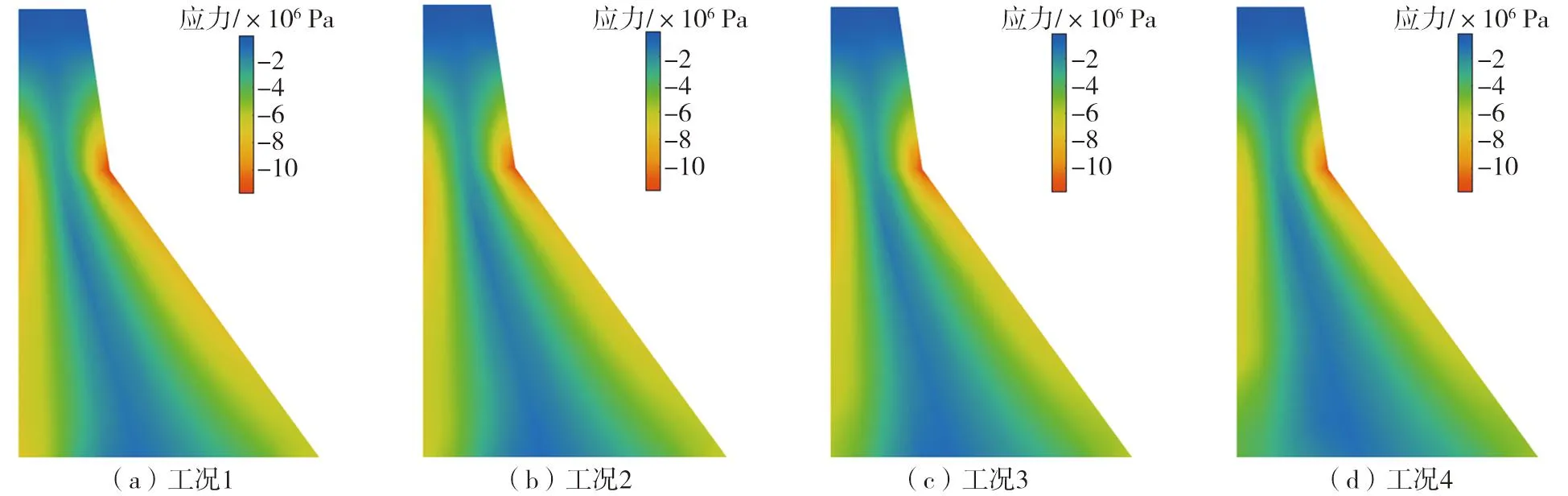
图17 各工况坝体最大压应力云图Fig. 17 Distribution of the maximum compressive stress on dam body under various cases
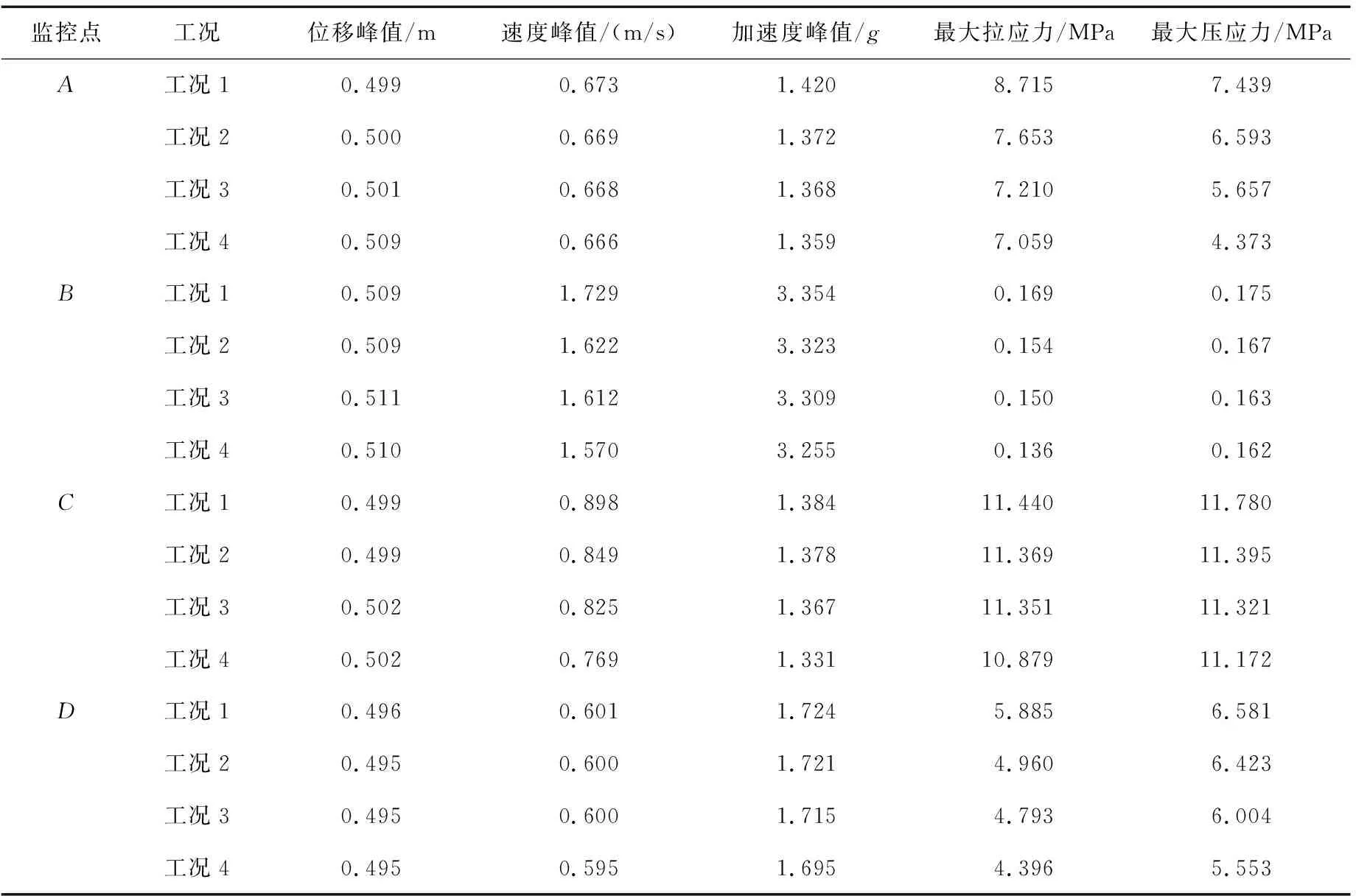
表2 各工况地震响应结果对比Table 2 Comparison of seismic response results under different working conditions
由表2可知,库底淤砂层对坝体节点的速度、加速度峰值、最大拉、压应力均有一定程度的影响。随着库底淤砂层厚度的增加,坝体各监控点的加速度峰值、最大拉、压应力逐渐减小,并且随着淤砂层厚度的增加,影响逐渐加大。淤砂层可降低坝体的地震反应,可能是由于淤砂层吸收了由坝基传至坝体的部分能量。
根据文献[26-27],可得到P波垂直入射时上行波在坝基表面上的透射系数。无淤砂层时求得透射系数为1.823,有淤砂层时求得P1波的透射系数为1.683(P2波衰减较快,这里忽略)。可以看出淤砂层的存在,一方面降低了P波上行波在坝基表面的透射系数,使得由坝基传至库水-坝体体系的能量减小;另一方面,淤砂层中孔隙水和固相骨架间的相对运动引起的附加阻尼,使得体系的能量消耗更多,因此淤砂层的存在使坝体的加速度和应力有所降低。
3 结语
本文将地震作用下库水-坝体-坝基相互作用问题看做是地震波入射时坝体的散射问题,提出了一种可综合考虑库水可压缩性、库底沉积淤砂层的库水-坝体-坝基系统的地震反应分析方法,并通过自编程序实现。以Koyna坝为对象,分析了Koyna坝在脉冲波和地震波作用下的响应,设计了4种工况,分析了库底淤砂层厚度对水坝地震反应的影响。得出以下结论:
1)Koyna地震波输入时,位移由低频波控制,其波长远大于坝体,坝体散射作用较小,坝顶相对于坝踵的位移放大系数要比速度和加速度放大系数小;但速度、加速度中高频成分丰富,坝体的散射对其有较大影响,坝顶、折坡处的速度和加速度峰值远大于坝踵和坝趾的峰值。
2)分析坝体各点输入地震波过程中的最大拉、压应力可知,坝体上游坝踵和下游折坡处应力较大,最大拉、压应力均出现在折坡处。
3)淤砂层厚度对坝体位移影响不大,但对加速度和坝体应力有影响,随着淤砂层厚度的增加,坝踵、下游折坡处和坝趾的加速度峰值以及最大拉、压应力逐渐减小。尤其在坝踵部位,由于淤砂层的影响,加速度和主应力峰值降幅最大。
本文算例仅为线性情形,未考虑坝体材料非线性和坝体-坝基间的接触非线性,非线性情形时淤砂层对坝体反应的影响需进一步研究。
